针对离线编程系统中机器人在世界坐标系下的位姿描述问题,提出一种利用对偶四元数精确标定机器人基坐标系的方法。首先在利用指数积公式建立机器人正运动学模型的基础上,推导了基于单位对偶四元数表示法的机器人基坐标系标定模型,该模型将世界坐标系与机器人基坐标系之间坐标转换的旋转与平移过程进行统一描述;其次,以对偶四元数的几何性质为约束条件,建立最小方差目标方程,引入拉格朗日乘子法求解最优的位姿变换矩阵;最后,对6自由度串联机器人进行了标定实验。实验结果表明,该标定方法可以有效解决工业应用环境中机器人的基坐标系标定问题,同时也为机器人手眼标定、多机器人协作基坐标系标定问题提供了参考依据。
In order to describe the robot poses in the world coordinate system of the off-line programming system, a precise calibration method of robot's base frame using dual quaternion was proposed. Firstly, on the basis of the robot kinematics model established by the product-of-exponential formula, a calibration model for robot's base frame using dual quaternion was derived, which obtains the unified description of robot poses between the world coordinate system and the robot's base frame. Then, with the dual quaternion constraints, the Lagrangian multiplier method was employed to obtain the optimum pose in solving a minimum-variance problem. Finally, calibration experiment on a serial 6-DOF industrial robot was performed, which indicated that the method is effective and easier to get solutions for robot's base frame calibration in industry environment. The calibration algorithm can not only provide theoretical reference but also provide useful advices to robot hand-eye system calibration and multi-robot coordination.
随着机器人离线编程技术在焊接、喷涂等加工行业中的应用和发展,机器人标定作为离线编程技术实用化的关键之一,是提高机器人定位精度有效的手段.为了实现机器人离线规划时实际作业对象与离线仿真环境中模型对象的调整与匹配,需要标定出机器人基坐标系与世界坐标系之间的转换关系,从而将机器人末端工具中心的位姿统一到世界坐标系下.按照测量手段,机器人基坐标系标定可细分为借助外部测量设备标定以及自标定两大类.
所谓自标定就是利用传感器信息来对机器人基坐标系与世界坐标系之间的转换关系进行标定的过程. Gan等[1]提出协作机器人基坐标系的标定方法. Wu等[2]在LBR iiwa14 R820平台上利用安装在机器人末端的摄像头对机器人基坐标系进行自标定.
借助外部测量设备进行标定,该方法操作简单、测量精度高.典型的空间坐标测量系统主要包括经纬仪、球杆仪、三坐标测量机、激光跟踪仪、测量臂等. Wang等[3]提出利用四元数表示法对机器人基坐标系进行标定.但以上算法均存在耦合误差,即旋转部分的误差会直接影响平移部分的计算精度.
为了克服传统方法处理旋转和平移运动相互分离的缺陷,考虑到对偶四元数理论可以同时描述旋转和平移运动,因此笔者利用对偶四元数理论进行机器人基坐标系标定.对偶四元数理论作为几何代数的一个子集,可以直观地表示空间方位、空间向量间的旋转、平移和缩放等关系,在机器人运动学[4-5]以及航天[6-7]等多个领域中得到了广泛的应用.
1 基于指数积公式的机器人正运动学建模n自由度串联机器人正运动学指数积方程[8]为
| $ {\mathit{\boldsymbol{g}}_{ST}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = {\exp ^{{{\hat \xi }_1}{\theta _1}}}{\exp ^{{{\hat \xi }_2}{\theta _2}}} \cdots {\exp ^{{{\hat \xi }_n}{\theta _n}}}{\mathit{\boldsymbol{g}}_{ST}}\left( {\bf{0}} \right) $ | (1) |
其中:S、T分别为机器人基坐标系和工具坐标系;Θ=(θ1, θ2, …, θn)T为关节变量向量,θi为第i个关节变量;
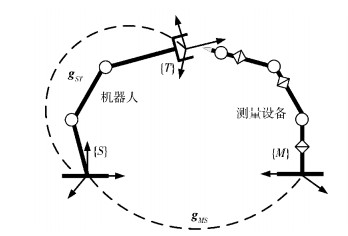
如图 1所示,在机器人基坐标系标定系统中,设定机器人末端执行器在世界坐标系下的位姿为gWT(Θ),采用gWS描述gWT(Θ) 与gST(Θ) 之间的变换关系,则有
| $ {\mathit{\boldsymbol{g}}_{WT}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = {\mathit{\boldsymbol{g}}_{WS}}{\mathit{\boldsymbol{g}}_{ST}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) $ | (2) |
|
图 1 机器人基坐标系标定系统相关坐标系 |
由于世界坐标系的选取是任意的,不妨选定测量设备坐标系作为世界坐标系,则标定机器人基坐标系与世界坐标系之间的变换关系转化为标定机器人与测量设备坐标系间的变换关系.因此,机器人基坐标系标定的实质就是求解变换矩阵gMS,使得
| $ {\mathit{\boldsymbol{g}}_{MT}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = {\mathit{\boldsymbol{g}}_{MS}}{\mathit{\boldsymbol{g}}_{ST}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) $ | (3) |
令RMT∈ℝ3×3、RMS∈ℝ3×3、RST∈ℝ3×3分别表示gMT、gMS、gST旋转部分,PMT∈ℝ3×1、PMS∈ℝ3×1、PST∈ℝ3×1分别表示其平移部分,则式 (3) 可表示为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{MT}}} & {{\mathit{\boldsymbol{P}}_{MT}}}\\ {\bf{0}} & 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{MS}}} & {{\mathit{\boldsymbol{P}}_{MS}}}\\ {\bf{0}} & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{ST}}} & {{\mathit{\boldsymbol{P}}_{ST}}}\\ {\bf{0}} & 1 \end{array}} \right] $ | (4) |
将式 (4) 展开得到机器人基坐标系标定模型:
| $ {\mathit{\boldsymbol{P}}_{MT}} = {\mathit{\boldsymbol{R}}_{MS}}{\mathit{\boldsymbol{P}}_{ST}} + {\mathit{\boldsymbol{P}}_{MS}} $ | (5) |
其中,PMT可借助外界测量设备直接得到,PST可通过式 (1) 求解得到.为了求解RMS和PMS,建立最小方差目标函数:
| $ f\left( {{\mathit{\boldsymbol{R}}_{MS}},{\mathit{\boldsymbol{P}}_{MS}}} \right) = \frac{1}{N}\sum\limits_{k = 1}^N {{{\left\| {{\mathit{\boldsymbol{P}}_{MT}} - {\mathit{\boldsymbol{R}}_{MS}}{\mathit{\boldsymbol{P}}_{ST}} - {\mathit{\boldsymbol{P}}_{MS}}} \right\|}^2}} $ | (6) |
其中:N为关节位形的测量个数,‖·‖表示欧氏距离.
2 基于对偶四元数理论的机器人基坐标系标定 2.1 对偶四元数对偶四元数是在四元数与对偶几何代数理论基础上提出的,可以解决一般性刚体运动 (旋转与平移) 问题[6].对偶四元数由两部分组成:
| $ \mathit{\boldsymbol{\hat q = r + }}\varepsilon \mathit{\boldsymbol{s}} $ | (7) |
其中:r=r0+ir1+jr2+kr3和s=s0+is1+js2+ks3均为纯四元数,称为实部与对偶部;i、j、k为虚数单位,满足i2=j2=k2=ijk=-1;ε为对偶单位,也称为Clifford算符,遵循ε≠0,ε2=0.根据对偶四元数的定义,单位对偶四元数满足条件:rTr=1,rTs=0.
旋转矩阵R和平移向量t分别用对偶四元数表示为
| $ \left[ {\begin{array}{*{20}{c}} 1 & {{{\bf{0}}^{\rm T}}}\\ {\bf{0}} & \mathit{\boldsymbol{R}} \end{array}} \right] = {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( \mathit{\boldsymbol{r}} \right)\mathit{\boldsymbol{Q}}\left( \mathit{\boldsymbol{r}} \right) $ | (8) |
| $ \mathit{\boldsymbol{t}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{t}}\\ 0 \end{array}} \right] = {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( \mathit{\boldsymbol{r}} \right)\mathit{\boldsymbol{s}} $ | (9) |
其中:
将机器人基坐标系标定模型构造为单位对偶四元数表示形式:
| $ {{\mathit{\boldsymbol{P'}}}_{MT}} = {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( \mathit{\boldsymbol{r}} \right)\mathit{\boldsymbol{Q}}\left( \mathit{\boldsymbol{r}} \right){{\mathit{\boldsymbol{P'}}}_{ST}} + 2{\mathit{\boldsymbol{W}}^{\rm{T}}}\left( \mathit{\boldsymbol{r}} \right)\mathit{\boldsymbol{s}} $ | (10) |
其中P′MT与P′ST分别为PMT与PST所对应的纯虚四元数.
将式 (10) 代入式 (6),得到目标方程:
| $ f\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) = \frac{1}{N}\left( {{\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{D}}_1}\mathit{\boldsymbol{r + }}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{D}}_2}\mathit{\boldsymbol{r + }}N{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s + }}{\mathit{\boldsymbol{D}}_3}} \right) $ | (11) |
其中:
| $ {\mathit{\boldsymbol{D}}_1} = - 2\sum\limits_{k = 1}^N {\left[ {{\mathit{\boldsymbol{Q}}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{P'}}}_{MT}}} \right)\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{P'}}}_{ST}}} \right)} \right]} $ | (12) |
| $ {\mathit{\boldsymbol{D}}_2} = 2\sum\limits_{k = 1}^N {\left[ {\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{P'}}}_{ST}}} \right) - \mathit{\boldsymbol{Q}}\left( {{{\mathit{\boldsymbol{P'}}}_{MT}}} \right)} \right]} $ | (13) |
| $ {\mathit{\boldsymbol{D}}_3} = \sum\limits_{k = 1}^N {\left( {\mathit{\boldsymbol{P}}_{ST}^{'{\rm{T}}}{{\mathit{\boldsymbol{P'}}}_{ST}} + \mathit{\boldsymbol{P}}_{MT}^{'{\rm{T}}}{{\mathit{\boldsymbol{P'}}}_{MT}}} \right)} = {\mathop{\rm const}\nolimits} $ | (14) |
采用拉格朗日函数法,以单位对偶四元数几何性质作为约束条件,构造辅助函数:
| $ \begin{array}{l} f\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}},{\lambda _1},{\lambda _2}} \right) = \frac{1}{N}\left[ {{\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{D}}_1}\mathit{\boldsymbol{r + }}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{D}}_2}\mathit{\boldsymbol{r + }}} \right.\\ \left. {N{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s + }}{\mathit{\boldsymbol{D}}_3} + {\lambda _1}\left( {{\mathit{\boldsymbol{r}}^{\rm{T}}}\mathit{\boldsymbol{r}} - 1} \right) + {\lambda _1}\left( {{\mathit{\boldsymbol{r}}^{\rm{T}}}\mathit{\boldsymbol{s}}} \right)} \right] \end{array} $ | (15) |
其中λ1和λ2为拉格朗日乘数.对式 (15) 求偏导:
| $ \begin{array}{*{20}{c}} {\frac{{\partial f\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}},{\lambda _1},{\lambda _2}} \right)}}{{\partial \mathit{\boldsymbol{r}}}} = }\\ {\frac{1}{N}\left[ {\left( {{\mathit{\boldsymbol{D}}_1} + \mathit{\boldsymbol{D}}_1^{\rm{T}}} \right)\mathit{\boldsymbol{r + D}}_2^{\rm{T}}\mathit{\boldsymbol{s}} + 2{\lambda _1}\mathit{\boldsymbol{r + }}{\lambda _2}\mathit{\boldsymbol{s}}} \right] = 0} \end{array} $ | (16) |
| $ \frac{{\partial f\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}},{\lambda _1},{\lambda _2}} \right)}}{{\partial \mathit{\boldsymbol{s}}}} = \frac{1}{N}\left[ {{\mathit{\boldsymbol{D}}_2}\mathit{\boldsymbol{r + }}2N\mathit{\boldsymbol{s + }}{\lambda _2}\mathit{\boldsymbol{r}}} \right] = 0 $ | (17) |
式 (17) 左乘rT,得到
| $ {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{D}}_2}\mathit{\boldsymbol{r + }}2N{\mathit{\boldsymbol{r}}^{\rm{T}}}\mathit{\boldsymbol{s + }}{\lambda _2} = 0 $ | (18) |
由于D2是反对称矩阵,故λ2=0.将λ2=0代入式 (18),得到
| $ \mathit{\boldsymbol{s = }} - \frac{{{\mathit{\boldsymbol{D}}_2}}}{{2N}}\mathit{\boldsymbol{r}} $ | (19) |
将式 (19) 代入式 (16),得到
| $ \mathit{\boldsymbol{Ar = }}{\lambda _1}\mathit{\boldsymbol{r}} $ | (20) |
其中
| $ \mathit{\boldsymbol{A = }}\frac{1}{2}\left[ {\frac{1}{{2N}}\mathit{\boldsymbol{D}}_2^{\rm{T}}{\mathit{\boldsymbol{D}}_2} - \left( {{\mathit{\boldsymbol{D}}_1} + \mathit{\boldsymbol{D}}_1^{\rm{T}}} \right)} \right] $ | (21) |
由式 (20) 可以看出,四元数r是4阶矩阵A的特征向量.假设λ1为对应的特征值,将式 (19) 和式 (20) 代入式 (11) 中,得到
| $ f\left( {\mathit{\boldsymbol{r}},\mathit{\boldsymbol{s}}} \right) = \frac{1}{N}\left( {{\mathit{\boldsymbol{D}}_3} - {\lambda _1}} \right) $ | (22) |
如果选择矩阵A对应的最大特征值λ1,式 (22) 取值最小.此时,利用式 (20) 求解出四元数r,式 (19) 解算s,代入式 (8) 及式 (9) 统一计算旋转矩阵R和平移向量t,得到标定结果RMS和PMS.
3 标定实验与数据分析在工业机器人实验环境下,对所提的标定方法进行了现场验证.以自主研发的6自由度串联机器人为研究对象,各关节处于参考零位时机器人构型及其连杆参数如图 2所示,测量靶标安装在机器人末端,测量工具为Faro关节臂,测量精度为0.016 mm/1.2 m,满足本实验系统精度要求.

|
图 2 6自由度串联机器人连杆参数 |
实验现场如图 3所示,在Faro测量臂的测量范围内,控制机器人运动,以末端靶标的中心作为测量目标点,获得20组目标点的三维位置.其中,目标点在{M}下的三维位置坐标gMT可由Faro测量臂直接读出,如表 1所示.目标点在{S}下的位置坐标gST可通过由示教器采集的关节转角 (θ1, θ2, …, θ6) 并结合式 (1) 可得到,关节转角如表 2所示.

|
图 3 机器人基坐标系标定实验环境 |
|
|
表 1 机器人末端位置坐标 |
|
|
表 2 机器人关节转角 |
假设机器人连杆参数无误差,利用式 (1)、式 (21)、式 (22)、式 (8)、式 (9) 计算得到旋转矩阵和平移向量分别为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} { - 0.9877} & {0.1564} & { - 0.0037}\\ { - 0.1564} & { - 0.9877} & {0.0012}\\ { - 0.0035} & {0.0017} & {1.0000} \end{array}} \right]}\\ {\mathit{\boldsymbol{t = }}{{\left[ {\begin{array}{*{20}{c}} {1108.937} & {345.908} & {66.532} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
最终得到描述机器人在世界坐标系与机器人基坐标系的位姿变换矩阵gMS.
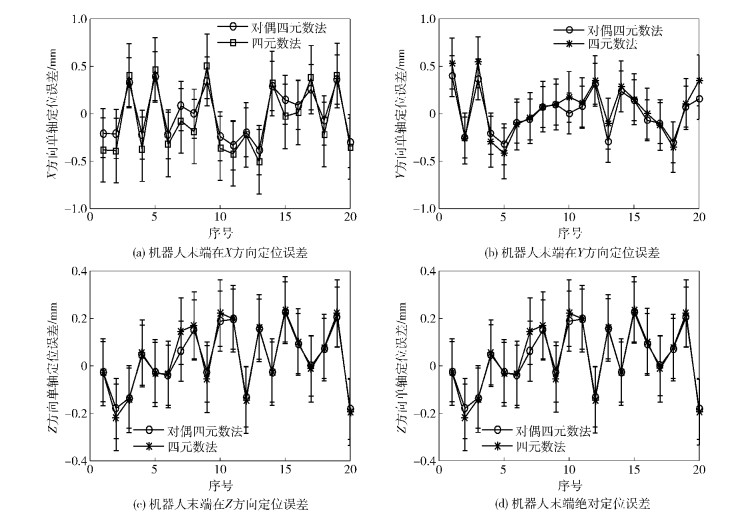
最后利用对偶四元数标定算法与文献[3]的四元数算法进行对比,对本节中的20组目标点进行精度验证,结果如图 4所示.
|
图 4 机器人基坐标系标定结果对比 |
图 4实验结果表明,对偶四元数标定精度高于文献[3]的四元数标定算法.这是由于在描述机器人位姿变换时,四元数法通常对其采取相互分离的计算方法,破坏了运动学问题的完整性,导致计算旋转矩阵和平移向量时存在耦合误差.而对偶四元数能够同时处理旋转矩阵和平移向量,利用对偶四元数统一描述机器人位姿变换问题,不仅使刚体旋转与平移运动的几何意义更加明确,而且降低了问题处理的复杂度,从而提高了标定精度.如果想进一步提高离线编程系统中机器人的绝对定位精度,还需对机器人几何参数进行标定.
4 结束语针对离线编程系统中机器人在世界坐标系下的位姿描述问题,笔者首次将对偶四元数应用于机器人基坐标系标定,精确、高效地完成了机器人基坐标系与世界坐标系之间的位姿转换问题.
1) 在利用指数积公式建立机器人正运动学模型的基础上,以对偶四元数表示法推导了机器人基坐标系标定模型.结果表明,由于对偶四元数能够统一表示机器人末端相对于世界坐标系与相对于机器人基坐标系之间的位置与姿态,因此克服了传统方法中旋转和平移相互分离引起的耦合误差,提高了标定精度.
2) 基于对偶四元数表示法推导的标定模型,适用于任何串联机器人的基坐标系精确标定.并且,该标定方法的优点是操作过程简单,标定环境要求不高,特别适合在工业生产中应用.
3) 由于基坐标系标定是机器人手眼标定、协作机器人基坐标系标定的共性问题,研究结果表明所提算法是一种有效的标定算法,对上述问题具有一定的参考价值.
| [1] | Gan Yanhui, Dai Xianzhong. Base frame calibration for coordinated industrial robots[J]. Robotics & Autonomous Systems, 2011, 59(7-8): 563–570. |
| [2] | Wu Liao, Ren Hongliang. Finding the kinematic base frame of a robot by hand-eye calibration using 3D position data[J]. IEEE Transactions on Automation Science & Engineering, 2017, 14(1): 314–324. |
| [3] | Wang Wei, Liu Fei, Yun Chao. Calibration method of robot base frame using unit quaternion form[J]. Precision Engineering, 2015, 41(3): 47–54. |
| [4] | Erol R, Mezouar Y. Kinematic modeling and control of a robot arm using unit dual quaternions[J]. Robotics & Autonomous Systems, 2016, 77(C): 66–73. |
| [5] |
倪振松, 廖启征, 魏世民, 等. 空间6R机器人位置反解的对偶四元数法[J]. 机械工程学报, 2009, 45(11): 25–29.
Ni Zhensong, Liao Qizheng, Wei Shimin, et al. Dual four element method for inverse kinematics analysis of spatial 6R maniputor[J]. Journal of Mechanical Engineering, 2009, 45(11): 25–29. |
| [6] | http://d.g.wanfangdata.com.cn/Thesis_D755879.aspx |
| [7] | Dong Hongyang, Hu Qinglei, Ma Guangfu. Dual-quaternion based fault-tolerant control for spacecraft formation flying with finite-time convergence[J]. ISA Transactions, 2016, 61: 87–94. doi: 10.1016/j.isatra.2015.12.008 |
| [8] | He Ruibo, Li Xiwen, Shi Tielin, et al. A kinematic calibration method based on the product of exponentials formula for serial robot using position measurements[J]. Robotica, 2015, 33: 1295–1313. doi: 10.1017/S026357471400071X |


