针对机会传感网络基于节点移动实现网络通信的特点,考虑到影响移动节点连通度的因素,提出了机会传感网络的移动节点连通度模型,实现了对移动节点连通度的刻画.在区域划分的机会传感网络中,分析了移动节点时间序列特征因子,得到与特征因子相关的影响移动节点连通度的因素.利用一元回归得到影响因素与时延的关系,通过回归组合分析得到移动节点的连通度模型.仿真结果表明,该模型能够反映机会传感网络移动节点的连通度.
According to the features of network communication through node movement in opportunistic sensor networks, a mobile node connectivity model was proposed by studying their impact factors, which dipicts connectivity of mobile nodes.In region-divided opportunistic sensor networks, the time series characteristic factors of mobile nodes were analyzed, and connectivity factors, related with them, were obtained.Monadic regression was employed to get the relationship between impact factors and delay. Based on the regression combination analysis, the mobile node connectivity model was constructed.Simulations show that the model can reflect the mobile node connectivity.
机会传感网络(OSN,opportunistic sensor networks) 是一种不需要源节点和目标节点之间存在完整链路,利用节点移动带来相遇机会实现通信的自组织网络[1],移动节点的缺失或失效可能导致整个网络的连通性下降,甚至出现网络失效的情况,移动节点的运行情况直接影响到网络的性能.这类网络适用于对延迟不敏感、无通信基础设施、需要快速组网的应用领域,如:车载网络[2]、城市及乡村网络[3]等. Shah等[4]将无线传感网络(WSNs,wireless sensor networks) 划分成3层结构,通过中间层的“数据驴”(Data MULEs,data mobile ubiquitous LAN extensions) 收集底层感知数据并投递至接入点(AP,access points),移动节点连接感知节点和Sink节点,在两者之间起到枢纽的作用;Sajadian等[5]利用节点通信半径、链路质量、节点能量和网络可达率研究WSNs的连通性,根据网络分簇,将连通因素进行线性组合,得到改善网络连通性的方法;OSN的连通性可以通过平均/最坏传输延迟、消息传输成功率等[6]网络性能参数体现;Pan等[7]提出节点相遇时间和节点相遇间隔时间是影响OSN性能的重要因素;Karamshu等[8]提出OSN中移动节点的相遇频率和平均连接时长可预测节点未来相遇情况.本文在上述研究基础上,定义移动节点连通度,分析影响移动节点连通度的相关因素,提出一种OSN的移动节点连通度模型.
1 移动节点连通度 1.1 移动节点连通度的描述OSN场景模型如图 1所示,区域节点采用随机路点(RWP,random way points) 移动模型,移动节点采用地图随机移动模型(MBM,map based movement),区域中的节点消息经移动节点携带并投递至Sink节点.
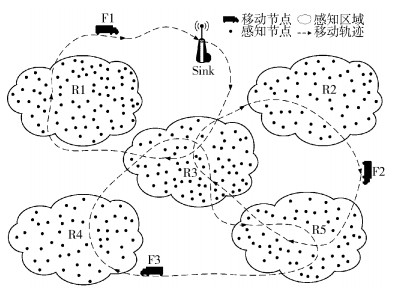
|
图 1 机会传感网络场景 |
定义1 移动节点连通度C是单位时间内该节点与其他节点相互通信的程度.
OSN具有复杂网络特性,可利用OSN的性能参数定量表征移动节点连通度,笔者选取移动节点消息投递至Sink节点的平均消息时延作为移动节点连通度的度量.
1.2 连通度的时序特征因子分析移动节点的连通时间序列能很好地反映移动节点的连通度.移动节点在T时间内的连通时间序列(1表示节点间处于连通状态,0表示非连通状态) 如图 2所示.
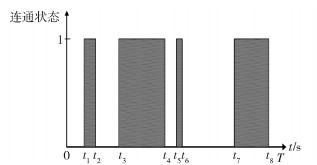
|
图 2 节点连通状态时间序列 |
不同的连通时间序列具有不同的序列特征,在文献[7-8]所述研究的基础上,考虑OSN连通性的特点,通过分析图 2所示的时间序列,找出以下4个不相关的特征因子,定义如下.
定义2 T是移动节点完成一次连通的时间.
定义3 N是时间T内移动节点发生的连接次数.
定义4 连通稳定度Cs是在时间T内连接时段t2-t1、t4-t3、t6-t5、t8-t7等时间序列的均方差.
定义5 断开稳定度Ds是时间T内断开时段t1-0、t3-t2、t5-t4、t7-t6、T-t8等时间序列的均方差.
虽然特征因子能够在一定程度上反映移动节点的连通程度,但由于部分特征因子不能直接测量,为定量分析带来不便.笔者通过对实验场景的分析,找出了影响上述4种特征因子且能反映移动节点连通度的主要因素包括移动节点经过的区域个数n、移动节点经过的各个区域节点总数F、节点的传输范围r、区域节点密度p、移动节点速率v.
1.3 因素相关性分析对选取的5个因素进行分组实验,每组实验重复10次,取其平均值,以确定各因素与移动节点消息平均投递时延的关系.区域个数n、区域节点总数F、节点传输范围r、区域节点密度p、移动节点速率v与移动节点消息平均投递时延间的关系如图 3所示.
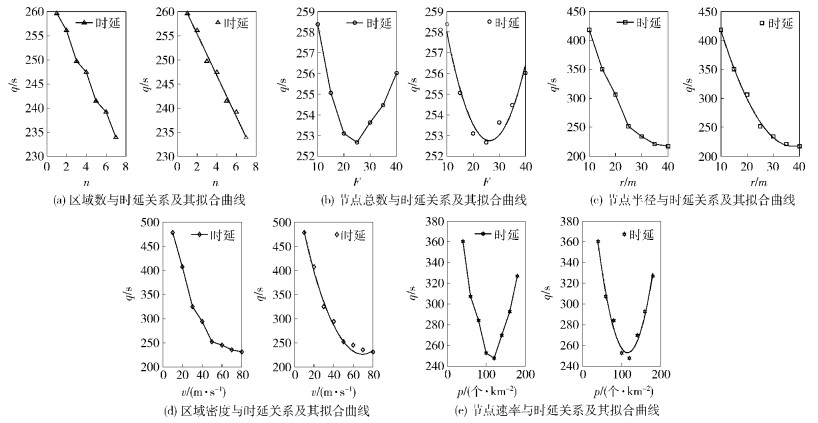
|
图 3 各因素与时延关系及其一元拟合曲线 |
从图 3可以看出,随着n、r、v的增加,平均时延减少,说明n、r、v对移动节点连通度有明显影响;F和p与平均时延是先降后增的关系.出现这种情况是由于节点间消息传递采用传染病路由,随着节点增多,节点消息缓存逐渐饱和,消息在网络中的平均时延不降反增.如表 1所示,p与F的相关性较大,其他因素间的相关性比较弱.
|
|
表 1 各因素间的非参数相关系数 |
根据各因素与平均时延的关系,可以确定几种备选拟合函数,其中:n的备选函数为线性函数、二次多项式函数或指数函数;F的备选函数为单项指数函数、双项指数函数或二次多项式函数;r的备选函数为单项指数函数、双项指数函数或二次多项式函数;p的备选函数为二次多项式、二次曲线函数或指数函数;v的备选函数为单项指数函数、双项指数函数或双曲线函数.通过对备选拟合函数的决定系数和标准差的对比分析,选出最佳拟合函数分别为线性函数、二次多项式函数和双项指数函数.对5个因素分别进行一元函数拟合,各因素函数最优拟合的决定系数和标准差如表 2所示,决定系数大于0.95,满足拟合要求.
|
|
表 2 函数拟合的决定系数和标准差对比 |
根据以上选择的拟合函数,求出各拟合函数的系数,得到最优化的一元函数分别为
| $ {f_1}(n) =-4.283n + 263.9 $ | (1) |
| $ {f_2}(F) = 0.019\;58{F^2} + (-1.034)F + 266.4 $ | (2) |
| $ {f_3}(r) = 0.261\;4{r^2} + (-19.75)r + 589.9 $ | (3) |
| $ {f_4}(p) = 0.018\;68{p^2} + (-4.323)p + 502.9 $ | (4) |
| $ {f_5}(v) = 573.8{{\rm{e}}^{-0.020\;58v}} + 11.31{{\rm{e}}^{0.030\;08v}} $ | (5) |
对应的拟合曲线如图 3所示.
2 移动节点连通度模型通过上述分析,将n、F、r、p、v作为影响移动节点连通度的主要因素,利用组合回归分析法对各因素的一元函数进行组合回归,得到移动节点连通度模型.
2.1 模型建立假设各因素的一元函数之间相互独立,式(6) 为移动节点连通度模型,其中μ为随机误差.
| $ \begin{array}{l} Y = {\beta _0} + {\beta _1}{f_1}({x_1}) + {\beta _2}{f_2}({x_2}) + \cdots + {\beta _i}{f_i}({x_i}) + \mu, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i > 0 \end{array} $ | (6) |
根据式(1)~式(5),得到对应的函数值,再对一元拟合函数进行线性组合回归,得到移动节点消息平均投递时延与一元拟合函数的组合函数.
| $ \begin{array}{l} q = 4.466 \times {10^{-15}} + 0.045{f_1}(n) + 0.005{f_2}(F) + \\ \;\;\;\;\;\;0.576{f_3}(r) + 0.387{f_4}(p) + 0.790{f_5}(v) \end{array} $ | (7) |
将式(1)~式(5) 代入式(7),得到移动节点连通度模型.
| $ \begin{array}{l} q = 4.466 \times {10^{-15}} + 0.045 \times (-4.283n + 263.9) + \\ 0.005 \times (0.019\;58{F^2}-1.034F + 266.4) + 0.576 \times \\ \;\;\;\;\;\;\;{\rm{(0}}{\rm{.261}}\;{\rm{4}}{r^2} - 19.75r + 589.9{\rm{) + 0}}{\rm{.387}} \times \\ \;\;\;\;\;\;{\rm{(0}}{\rm{.018}}\;{\rm{68}}{p^2} - 4.323p + 502.9{\rm{) + 0}}{\rm{.790}} \times \\ \;\;\;\;\;\;\;\;\;\;\;(573.8{{\rm{e}}^{ - 0.020\;85v}} + 11.31{{\rm{e}}^{0.030\;08v}}) \end{array} $ | (8) |
在组合回归过程中,需要对变量进行多重共线性判断,可利用膨胀因子法对多重共线性进行判断.解释变量Xj的参数估计
| $ Var({\hat \beta _j}) = \frac{{{\sigma ^2}}}{{\sum {x_j^2} }}\frac{1}{{1-R_j^2}} = \frac{{{\sigma ^2}}}{{\sum {x_j^2} }} \times {H_j} $ | (9) |
其中:Hj为变量Xj的方差膨胀因子,Rj2为多个解释变量辅助回归的可决系数.一般方差膨胀因子越大,表示变量之间的多重共线性越严重;相反,方差膨胀因子越趋近1,共线性现象就越弱.如果方差膨胀因子大于或等于10,表示解释变量之间存在明显的多重共线性.
| $ {H_j} = \frac{1}{{1-R_j^2}} $ | (10) |
对5个函数变量进行共线性分析,得到膨胀因子H分别为1.844、2.924、1.081、2.072、1.064.可见,模型中变量间的多重共线性问题并不严重,同时,对模型的残差进行适应性检验,如图 4所示的P-P图可以检验模型的残差是否符合正态分布.当残差符合正态分布时,P-P图中各点近似为一条直线分布,说明该模型是合适的,符合假设条件.
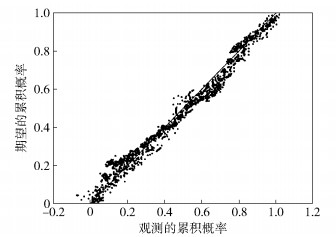
|
图 4 回归标准化残差的P-P图 |
在机会网络环境(ONE,opportunistic networks environment) 仿真平台上进行实验仿真,获得实验数据,将数据导入MATLAB仿真工具和SPSS (statistical product and service solutions) 软件进行分析,验证移动节点连通度模型的合理性.
3.1 实验设计在ONE中搭建连通性良好、一般和较差3种场景,区域内节点采用RWP移动模型,移动节点采用MBM模型,通过调整移动节点、区域、Sink节点之间的关系来改变移动节点连通度,当连通性良好时,所有移动节点都能直接与Sink节点通信,随着连通性变差,能直接与Sink节点通信的移动节点越来越少,网络仿真参数如表 3所示.在3种场景下,分别对影响移动节点连通度因素进行分组实验,将各场景仿真数据与模型拟合数据进行对比分析,结果如图 5所示.

|
图 5 机会传感网络3种网络场景下的仿真对比 |
|
|
表 3 仿真参数 |
由图 5可知,当网络连通性良好时,本文提出的OSN移动节点连通度模型能很好地随移动节点连通度的变化而变化,仿真数据与拟合数据基本吻合,同时相对误差很小;在网络连通性变差的过程中,仿真数据与拟合数据间出现抖动,误差逐渐变大,3种场景下的平均时延和误差如表 4所示.
|
|
表 4 不同连通性下的模型平均时延和误差对比 |
随着网络连通性变差,仿真数据与拟合数据的误差慢慢变大,但该模型还是能够反映移动节点连通度的情况.出现上述情况的主要原因是OSN连通度下降,导致网络的稳定性下降,消息平均时延增加,传输过程中的错误率变高,底层的感知消息很难准确投递至Sink节点,整个网络运行情况变得更加复杂,不确定因素增多,也是导致移动节点连通度模型拟合数据与仿真数据误差变大的原因.
4 结束语研究了OSN移动节点的连通度,分析了影响移动节点连通度的因素,提出OSN移动节点连通度模型,仿真实验表明该模型是合理的.本文中部分影响移动节点连通度的因素间存在相关性,且只选取了消息平均投递时延来度量移动节点的连通度,未考虑消息投递成功率,这两方面将在后续工作中进行深入分析和研究.
| [1] |
熊永平, 孙利民, 牛建伟, 等. 机会传感网络[J]. 软件学报, 2009, 20(1): 124–137.
Xiong Yongping, Sun Limin, Niu Jianwei, et al. Opportunistic networks[J]. Journal of Software, 2009, 20(1): 124–137. doi: 10.3724/SP.J.1001.2009.00124 |
| [2] | Pereira P R, Casaca A, Rodrigues J J P C, et al. From delay-tolerant networks to vehicular delay-tolerant networks[J]. Communications Surveys & Tutorials, IEEE, 2012, 14(4): 1166–1182. |
| [3] |
刘期烈, 胡春凤, 朱德利, 等. 机会网络节点兴趣社区检测及路由策略[J]. 北京邮电大学学报, 2014, 37(3): 62–66.
Liu Qilie, Hu Chunfeng, Zhu Deli, et al. Interest community detecting method and routing scheme in opportunistic networks[J]. Journal of Beijing University of Post and Telecommunications, 2014, 37(3): 62–66. |
| [4] | Shah R C, Roy S, Jain S, et al. Data mules:modeling and analysis of a three-tier architecture for sparse sensor networks[J]. Ad Hoc Networks, 2003, 1(2): 215–233. |
| [5] | Sajadian S, Ibrahim A, de Freitas E P, et al. Improving connectivity of nodes in mobile WSN[C]//IEEE International Conference on Advanced Information Networking and Applications, AINA 2011.[S. l.]:IEEE, 2011:364-371. |
| [6] | Boldrini C, Conti M, Jacopini J, et al. Hibop:a history based routing protocol for opportunistic networks[C]//IEEE International Symposium on World of Wireless, Mobile and Multimedia Networks, WoWMoM 2007.[S.l.]:IEEE, 2007:1-12. |
| [7] | Pan H, Chaintreau A, Scott J, Gass R, et al. Pocket switched networks and human mobility in conference environments[C]//ACM SIGCOMM Workshop on Delay-Tolerant Networking. Philadelphia:ACM, 2005:244-251. |
| [8] | Karamshuk D, Boldrini C, Conti M, et al. Human mobility models for opportunistic networks[J]. Communications Magazine, IEEE, 2011, 49(12): 157–165. doi: 10.1109/MCOM.2011.6094021 |


