在执行机构对目标物体进行自主定位过程中,定位误差的实时计算、误差修正和状态分析往往比较困难.为此,提出基于三帧差法的Kalman滤波算法进行末端动态捕捉,利用反向传输(BP)神经网络分类思想进行目标识别,基于点云库的点云提取和处理算法,获得末端和目标物体的空间坐标.最后,将散乱点群进行网格化和3D空间插值.实验结果表明,算法能实时检测并跟踪运动末端,预测精度达到99%,且目标物体的识别率为99%,并可在短时间内修正定位误差,使末端中心点逐步收敛到目标质心,自主定位成功.用三维拟合法对算法的有效性进行验证,并对定位过程进行了状态分析.新算法能完成执行机构的自主定位,省去了相机标定过程,提高了系统效率.
The real-time calculation of positioning error, error correction and state analysis is a difficult challenge in the process of end-effector autonomous positioning. In order to solve this problem, the Kalman filtering based on three-frame subtraction is proposed to capture the moving end-effector. Back propagation (BP) neural network is adopted to recognize the target. And 3D information extraction based point cloud library (PCL) is described to calculate the space coordinates of the end-effector and the target. The scattered points are processed by gridding and interpolation. Experiments demonstrate that the end-effector positioning can be corrected in a short time. The prediction accuracy of position reaches 99% and the recognition rate of 99% is achieved for target object. Furthermore, the gradual convergence of end-effector center (EEC) to the target center (TC) shows that the autonomous positioning is successful. The algorithm effectiveness is also validated by 3D fitting, but the camera calibration is not required. The system efficiency is improved.
通过视觉系统指导执行机构对目标物体进行定位控制,根据定位误差信息不断修正执行机构各关节的运动.现有的研究工作,Izadi等[1]提出基于Kinect技术表面纹理实时重建. Kahl等[2]从运动视觉分析的角度寻求多视重构的求解方法,构建稀疏点云和初始网格. Izadi等[3]利用单个移动和4个固定的Kinect来获取点云数据,用迭代最近点算法解决点云对齐和模板拟合问题.笔者提高了执行机构的自主操作性和对环境的自适应性;方便了定位过程的可视化监测和定位误差的实时计算与分析.
1 Kinect工作原理在水平方向安置3个镜头,左右两侧分别是红外发射器和互补金属氧化物半导体(CMOS,complementary metal oxide semiconductor) 红外接收器,识别的是一个“深度场”.中间镜头是红绿蓝(RGB,red green blue) 相机,可获取彩色影像;这样就构成了3D深度传感器,利用深度图像可以很容易提取出3D点云数据,如图 1所示. Kinect的数据采集技术是非接触式的,采用光编码技术进行3D侦测,获取深度影像信号.激光照射到物体表面会产生高度随机的散斑,场景中不同点到摄像头的距离不同,散斑图案也不同. Kinect系统中,这一差别被用来对场景空间的任意点进行标记.通过空间中物体上的散斑图案即可计算出物体所在的确切位置,即深度信息. Kinect红外发射器通过镜头前的光栅将激光均匀投射在测量空间中,再经由红外线接收器记录下空间中经过编码的散斑.然后经过晶片执行复杂的并行逻辑运算生成具有3D深度信息的图像.

|
图 1 点云数据(视角可调整) |
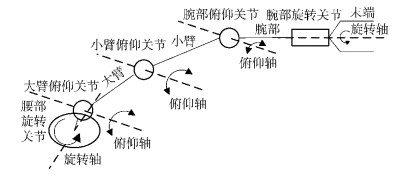
以5自由度执行机构为例,具有5个旋转轴,5个自由度,6个关节和3个连杆. 5个旋转轴分别为腰部旋转轴,大臂俯仰轴,小臂俯仰轴,腕部俯仰轴和腕部旋转轴,如图 2所示.建立正运动学模型,由执行机构各关节角度推算末端运动轨迹,定义为
|
图 2 执行机构结构 |
| $ \begin{array}{l} ^0{\boldsymbol{T}_N}{ = ^0}{\boldsymbol{T}_N}(v){ = ^0}{\boldsymbol{T}_1}^1{\boldsymbol{T}_2}{ \cdots ^{N - 1}}{\boldsymbol{T}_N} = \\ \prod\limits_{i = 1}^N {^{i - 1}{\boldsymbol{T}_i}} = \left[ {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}}\\ {{n_z}}&{{o_z}}&{{a_z}}&{{p_z}}\\ 0&0&0&1 \end{array}} \right] \end{array} $ |
其中:
采用三帧差法从序列图像中检测出像素变化区域并从静态背景中提取出运动目标.可更好处理环境噪声,“双影”的处理效果也优于相邻二帧差法.对得到的差分图像通过选取适当的阈值进行二值化.进行形态学腐蚀和膨胀去除空洞.
在视频帧中,末端的运动是一离散时间的动态系统,状态向量为
| $ {\boldsymbol{x}_k} = {[x(k), y(k), x'(k), y'(k)]^{\rm{T}}} $ |
其中x(k) 和y(k) 分别为末端质心在X、Y轴上的坐标,x′(k) 和y′(k) 分别为末端质心在X、Y轴上的速度.令观测向量为zk=[xc(k), yc(k)]T,xc(k) 和yc(k) 分别为末端质心在X、Y轴上的观测值.通过状态空间动态方程可表示为
| $ {\mathit{\boldsymbol{x}}_k} = {\phi _k}{\mathit{\boldsymbol{x}}_{k-1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}{\mathit{\boldsymbol{u}}_{k-1}} + {\mathit{\boldsymbol{b}}_{k-1}}, {z_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k} $ | (1) |
其中:xk为系统状态,uk-1为系统的控制量,zk为测量值,bk-1和vk分别为过程和测量噪声,Φk为系统状态转移矩阵,Γk为控制系数变换矩阵,Hk为测量转移矩阵.
根据物理学运动方程来估计目标位置的方法,对下一个状态进行预测和修正.估计出均值和协方差的后验概率密度函数.状态预测方程为
| $ \mathit{\boldsymbol{x}}_k^-= {\phi _k}\mathit{\boldsymbol{x}}_{k-1}^ + + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}{\mathit{\boldsymbol{u}}_{k-1}} $ | (2) |
协方差预测方程为
| $ \boldsymbol{P}_k^-= {\boldsymbol{\phi} _k}\boldsymbol{P}_{k-1}^ + \boldsymbol{\phi} _k^{\rm{T}} + {\boldsymbol{Q}_{k-1}} $ | (3) |
Kalman增益矩阵为
| $ {\boldsymbol{K}_k} = \boldsymbol{P}_k^- \boldsymbol{H}_k^{\rm{T}}{[{\boldsymbol{H}_k}\boldsymbol{P}_k^-+ \boldsymbol{H}_k^{\rm{T}} + {\boldsymbol{R}_k}]^{ -1}} $ | (4) |
协方差估计为
| $ {\boldsymbol{P}_k} = {[\boldsymbol{I}-{\boldsymbol{K}_k}{\boldsymbol{H}_k}]^{ -1}}\boldsymbol{P}_k^ - $ | (5) |
状态估计为
| $ \boldsymbol{x}_k^ + = \boldsymbol{x}_k^-+ {\boldsymbol{K}_k}({\boldsymbol{z}_k}-{\boldsymbol{H}_k}\boldsymbol{x}_k^-) $ | (6) |
其中:xk-为tk时刻的状态预测,xk-1+为tk-1时刻的状态测量,xk+为tk时刻的状态测量,Pk-为tk时刻的预测协方差矩阵,Pk为tk时刻的测量协方差矩阵,Pk-1+为tk-1时刻的测量协方差矩阵,Qk-1为过程噪声协方差矩阵,Rk为测量噪声协方差矩阵,Kk为Kalman增益矩阵.在每次完成预测和修正后,由后验估计预测下一时刻的先验估计,重复以上步骤.
4 定位目标识别以圆柱形物体(CTO,cylindrical target object) 为例,末端和CTO出现在同一幅图像和视频流中.提取CTO的特征参数有周长、面积、最长轴、方位角、边界矩阵、形状系数和轮廓点数.周长可用其外边界的相邻2像素之间的距离之和表示;面积用目标区域像素的个数来表示;最长轴为外边界上距离最大的2像素点的连线;方位角为目标区域的最长轴与x轴的夹角;边界矩阵为包围目标区域的最小矩阵;形状系数为面积和周长平方的比值;轮廓点数为勾勒出轮廓所需要的像素点数.
采用反向传输(BP,back propagation) 神经网络学习算法,提取的特征向量作为训练样本,神经网络作为分类器代替特征向量间的欧氏距离判别,实现目标识别.
1) 输入输出层:输入层节点个数为7,输入向量中的元素分别为{轮廓点数, 周长, 面积, 最长轴, 方位角, 边界矩阵, 形状系数}.输出层节点个数为3,输出向量的元素为{cylinder, square, spherical},设置归一化数值分别为0.1、0.2和1.
2) 隐含层:采用具有对数特性和purelin函数的双隐层结构,隐含层1节点个数为20,隐含层2节点个数为3,输出层采用线性激励函数.
3) 样本集:从某一个角度拍摄方形或球形物体,容易与CTO混淆,所以增加样本图像类别,采集方形和球形物体.圆柱形共有30种不同物体,每种含20个不同角度;方形物体共10种不同物体,每种含20个不同角度;球形共10种不同物体,每种含20个不同角度.
识别完成后,需要计算目标质心(TC,target center),CTO的形状是规则的,因此质心也就是形心.质心的空间位置为末端定位的目标位置. TC坐标计算为
| $ \bar x = \frac{{\sum\limits_{{i_b}}^{{i_e}} {\sum\limits_{{j_b}}^{{j_e}} i ({p_{ij}}-T)} }}{{\sum\limits_{{i_b}}^{{i_e}} {\sum\limits_{{j_b}}^{{j_e}} {({p_{ij}}-T)} } }}, \bar y = \frac{{\sum\limits_{{i_b}}^{{i_e}} {\sum\limits_{{j_b}}^{{j_e}} j ({p_{ij}}-T)} }}{{\sum\limits_{{i_b}}^{{i_e}} {\sum\limits_{{j_b}}^{{j_e}} {({p_{ij}} - T)} } }} $ | (7) |
其中:ib和ie分别为目标物体像素行计数的最小值和最大值,jb和je分别为列像素的最小值和最大值,T为自适应阈值,pij为目标物体像素的灰度值.
5 三维重建 5.1 点云采集图像帧中提取的运动末端是定位系统的主动对象,图像识别的目标物体属于定位系统中的被动对象.被动对象和主动对象通过第3、4部分确定后,通过Kinect获得它们的点云数据.点云库(PCL,point cloud library) 是一项集点云获取与处理、滤波、特征提取、表面重建和点云配准以及点云融合等功能为一体的开源点云处理库. Kinect点云坐标数据的采集模型,假设Kinect测量空间中一点P到相机的距离为draw,draw表示深度图像中的深度值.点P在空间中的实际位置为
| $ d = K\tan (H{d_{{\rm{raw}}}} + L)-O $ | (8) |
其中:d和draw的单位为cm,H=3.51O-4 rad,K=12.36 cm,O=3.7 cm,L=1.18 rad.根据式(8) 的计算,从Kinect中提取出P点的完整的3D坐标矢量(x, y, z)/cm.设P点在帧图像的投影位置为(u, v),则其3D坐标为
| $ x = (u-{u_0}){f_x}d, y = (v-{v_0}){f_y}d, z = d $ | (9) |
其中:
每帧图像中的目标点云包含近10万个点.这样庞大无序的数据的处理需要消耗大量时间和硬件资源,影响算法速度.采用基于密度分析的方法预处理,可去除3万左右的噪声点云. Kinect获取的点云数据分布并不均匀,每个点到其邻域内其他点的平均距离近似服从高斯分布,其形状由全局的邻域平均距离均值μ和标准差σ决定.点云数据存在着部分离群点,其邻域点数量较少,邻域平均距离s较大.通过计算每个点到其邻近点的平均距离,若平均距离在标准范围(由均值μ和标准差σ确定) 之外,该点被定义为离群点,应去除.邻域平均距离的概率密度函数为
| $ f({s_i}) = \frac{1}{{\sqrt {2{\rm{\pi }}\sigma } }}\exp \left( {-\frac{{{{({s_i}-\mu )}^2}}}{{2{\sigma ^2}}}} \right), i = 1, 2, 3, \cdots $ | (10) |
其中:si为任意点的邻域平均距离;μ为邻域平均距离均值;σ为标准差.
将每个点的邻近点数设为m,标准差倍数设为n,当一个点的邻域平均距离超出全局平均距离nσ以上时,则该点被标记为离群点并移除. m值越大,n值越小,可判定为离群点的噪声越少,m和n值通过实验确定(分别设定为25和4),避免离群点去除不完整或去除过度.
目标点云获得后,进行三角面片曲面拟合,即网格生成.由于得到的数据云是密集的散乱点群,将三角形的各个顶点拉伸去拟合密集散乱点群,形成雕刻曲面,即3D空间插值.
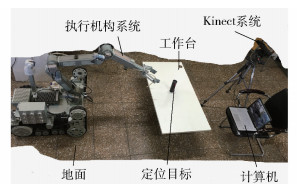
6 实验与分析系统的实验平台由计算机(ACER TMP455, 16 G memory, 500 G SSD)、执行机构系统和Kinect三部分构成,如图 3所示.计算机软件有VC++2010、OpenNI和Kinect for Windows sdk v1.7.
|
图 3 实验平台 |
将视频转换为图像帧格式(480×640×3),共73帧.利用Kalman滤波估计末端运动状态,从而获得末端在图像帧中的位置. 图 4示出了末端实际的位置和估计位置之间的关系.由73个中心点的图像像素坐标拟合成的曲线,反映中心点在图像中的位置变化情况.实线表示末端实际位置,虚线表示Kalman估计的末端运动位置.在起始一段时间内的跟踪较为平稳;在中间的运动过程中,末端的实际轨迹与估计轨迹存在一定的像素误差,最大误差为6像素,这是由于末端的变速运动造成的.但在结束的一段时间内逐步修正过来,使基本跟踪趋势保持一致.

|
图 4 位置估计 |
末端的实际位置与估计位置趋势的一致性表明此算法能预测末端位置.基于三帧差法的Kalman滤波提高了系统对环境自适应能力,对工作场景并不关注,只检测场景中运动的目标.
6.2 识别实验与分析提取物体的边缘轮廓,根据7类特征参数的几何描述分别进行数值计算,从而获得样本集.样本的维数为1 000×8(圆柱形600,方形200,球形200).训练集的维数为900×8(圆柱形540,方形180,球形180),测试集的维数是100×8(圆柱形60,方形20,球形20). BP网络迭代47次收敛.
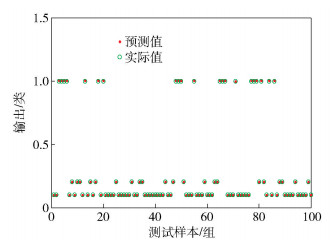
目标识别情况如图 5所示.输出值0.1、0.2和1分别表示圆柱形、方形和球形目标.圆柱形物体有59个识别正确,1个被误认为方形(识别率98.3%);方形20个全部识别正确;球形20个全部识别正确.所以,测试样本的识别率为0.99.从测试集中随机抽取一个分类为0.1的目标并计算TC,TC坐标为(507, 306)/pixel.
|
图 5 识别结果 |
图像的识别率越高,说明提取的特征越全面和关键,BP网络的参数和结构也越合理.无须精确的数学模型,具有学习能力.但网络结构的选择没有统一的理论指导.
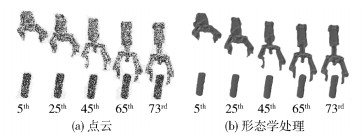
6.3 点云拟合经计算,圆柱TC三维坐标为(213.5 mm, -3.8 mm, 825.2 mm).在73帧视频中,提取动态末端中心点(EEC,end-effector center) 三维坐标如表 1所示. 表 1中x、y、z为EEC相对于基座坐标系的坐标. EEC逐渐收敛到TC坐标,x、y、z方向的绝对误差分别为213.5-212.6=0.9 mm,-3.5+3.8=0.3 mm,825.2-823.9=1.3 mm. x方向的理论计算值是不变的,但实验数据在一定范围内有所波动,随机最大波动为225.5-208.3=17.2 mm. y方向理论计算值是递减的,实验数据也是呈递减趋势变化. z方向的理论计算值是呈递增趋势变化的,实验数据的整体趋势是递增的,但在一些连续帧中是不变的或来回波动.数值的波动是由Kinect相机本身像素精度不高引起的.末端和目标三维点云如图 6(a)所示,三角面片化和形态学处理如图 6(b)所示.受篇幅限制,只展示第5、25、45、65和73帧的点云拟合.
|
图 6 拟合结果 |
|
|
表 1 EEC的坐标 |
EEC与TC之间的差值表示定位误差,为指导执行机构运动控制提供参考数据. EEC逐步逼近TC,根据末端(夹持器最大开合287 mm) 的定位需求,x、y、z方向的最大允许误差分别为20 mm,25 mm和20 mm,在此范围内表明定位成功.
6.4 对比实验本文方法与文献[1-3]方法进行比较可知,1) 可应对大运算量;2) 对光源要求不高,主要受阳光直射的影响,这是因为Kinect投射出近红外光源;3) 算法效率提高,神经网络对数学模型的依赖程度较低;4) 重建精度与文献[1, 3]不相上下,相机标定误差、目标识别和末端的提取等都会影响三维重建的精度.不同方法下的性能比较如表 2所示.
|
|
表 2 不同方法下的性能比较 |
采用简易深度成像设备Kinect对执行机构末端进行自主定位控制,并对其定位过程进行三维重建.提出一种基于三帧差法的Kalman滤波算法对末端进行检测和状态估计;基于BP神经网络分类思想对目标物体进行识别;根据EEC与TC间的定位误差指导执行机构的运动控制,整个过程无须人工干预;点云拟合验证了自主定位算法的有效性,方便对整个定位过程的可视化监测.
| [1] | Izadi S, Newcombe R A, Kim D. Kinectfusion:real-time dynamic 3D surface reconstruction and interaction[C]//Proceedings of Association for Computing Machinery's Special Interest Group on Computer Graphics and Interactive Technologies. Vancouver:[s. n.], 2011:23. |
| [2] | Kahl F, Hartley R I. Multiple-view geometry under the L∞norm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 30(9): 1603–1617. |
| [3] | Izadi S, Kim D, Hilliges O, et al. Kinectfusion:real-time 3D reconstruction and interaction using a moving depth camera[C]//Proceedings of the 24th Annual ACM Symposium on User Interface Software and Technology. Santa Barbara:[s. n.], 2011:559-568. |
| [4] |
胡燕祝, 李雷远. 基于多层感知人工神经网络的执行机构末端综合定位[J]. 农业工程学报, 2016, 1(32): 22–27.
Hu Yanzhu, Li Leiyuan. Series actuator end integrated positioning analysis based-on multilayer perceptron neural network[J]. Transactions of the Chinese Society of Agricultural, 2016, 1(32): 22–27. |


