2. 韩国釜山国立大学 电子工程系, 韩国 釜山
为了应对运动目标跟踪任务中目标的尺度、光照变化和形变等情况,提出了一种基于混合特征的运动目标跟踪方法--SoH-DLT,综合考虑了运动目标的轮廓特征和细节特征.在粒子滤波跟踪过程中引入方向直方图描述目标轮廓特征,保证与目标最相似的粒子在尺度、光照变化和形变的情况下仍能获得较高的置信度,并作为跟踪结果输出.结合深度学习获得的高层特征和具有尺度不变性的加速鲁棒特征计算粒子权重,提高了复杂运动场景下目标跟踪的准确度,强化了SoH-DLT方法对尺度变化运动目标跟踪的鲁棒性.实验结果表明,SoH-DLT与其他方法相比获得了更好的跟踪效果.
2. Department of Electronics Engineering, Korea Pusan National University, Busan, Korea
In order to deal with scale variation, illumination changes and deformation of the target in tracking tasks, a visual tracking algorithm based on mixed features, called SoH-DLT, was proposed, considering both the contour features and detail features. Orientation histogram is introduced to describe the contour features of candidate samples in the process of particle filter, ensuring that the particle which is the most similar with the target can still get a high degree of confidence and can be output as the result of tracking in the case of scale, illumination changes and deformation. Speed-up robust features (SURF) feature and high-level features from deep learning are integrated to calculate the weights of particles, improving the tracking accuracy in complex scenes and enhancing the robustness of SoH-DLT to scale variation. Experiments show that SoH-DLT algorithm has better tracking performance than the contrast algorithms in both quantitative and qualitative evaluation.
运动目标跟踪[1]是计算机视觉领域的一个重要研究课题,在智能交通、视频监控、虚拟现实等众多领域有着重要应用价值.然而,运动目标所处环境的复杂性及目标本身的不确定性给跟踪问题带来了很大的挑战.近几年,基于深度学习的目标跟踪方法通过自动提取目标特征[2]获得更有效的图像特征表示[3],实现了更准确的跟踪.笔者提出基于混合特征的运动目标跟踪方法,将深度学习获得的高层特征与加速鲁棒特征(SURF,speed-up robust features) 结合起来,增强该方法对目标尺度变化的鲁棒性;粒子滤波跟踪过程中,对目标和各候选样本提取轮廓特征,为粒子的置信度计算提供参考,进一步提高了目标跟踪的准确性,并给出了实验结果和分析.
1 SoH-DLT运动目标跟踪方法SoH-DLT分为线下训练和线上跟踪2个部分. SoH-DLT的方法结构如图 1所示.在线下特征学习过程中,使用大量的数据训练堆栈式去噪自编码器[4](SDAE,stacked denosing autoencoder),获得通用的图像高层特征.在线上跟踪过程中,构建神经网络用于粒子滤波过程中粒子的权重计算,并依据线下训练获得的特征参数对其进行初始化.当新的一帧到来时,使用SURF特征点映射矩阵对该神经网络进行微调.另外,分别建立目标模板与各候选样本的方向直方图,并计算各候选样本与目标模板的相似度,以此作为各粒子重要性的参考.
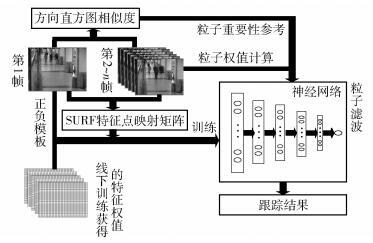
|
图 1 SoH-DLT方法结构 |
SoH-DLT对于运动目标的特征提取分为2个方面:1) 目标的轮廓特征,采用方向直方图来进行描述(见2.1节);2) 目标的细节特征,包括线下深度学习获得的高层特征和线上提取的SURF特征(见2.2节). SoH-DLT整合这2种特征,得到目标的混合特征,从而在粒子滤波过程中能更精确地区分目标和背景.
2.1 基于方向直方图的特征提取引入方向直方图来描述图像样本的梯度方向信息,提取轮廓特征,同时计算当前样本与目标模板的相似度,并将其作为后续运动估计过程中粒子重要性的参考.梯度方向是指某像素在y方向和x方向梯度形成的角度,对一个大小为a×b的灰度图像,用{θij}i∈[1, a], j∈[1, b]表示各像素的梯度方向角为
| $ {\theta _{ij}} = {\rm{arctan}}\left( {\frac{{\partial {g_{ij}}/\partial y}}{{\partial {g_{ij}}/\partial x}}} \right) $ | (1) |
其中:gij为(i, j) 像素的灰度值,∂gij/∂y为gij在y方向的梯度,∂gij/∂x为gij在x方向的梯度.
方向直方图通过将梯度方向角划分为不同的区间来确定.其计算为
| $ {T_k} = \left\lfloor {{\theta _{ij}}/\Delta \theta } \right\rfloor $ | (2) |
其中:{Tk}k∈[1, n]为各区间,Δθ为区间间距.方向直方图即为统计各个方向编码Tk在图像中出现的概率.
为了增大密度估计的鲁棒性,使距离目标中心更近的像素分配更大的权重,距离目标中心较远的像素分配较小的权重,对方向直方图进行加权处理,加权后的方向直方图第k个区间出现的概率pk为
| $ {p_k}\left( y \right) = {T_h}\sum\limits_{i = 1}^{{n_h}} {k\left( {\left\| {\frac{{y - {x_i}}}{h}} \right\|} \right)} \delta \left[ {b\left( {{x_i}} \right) - k} \right] $ | (3) |
其中:y为样本的中心,{xi}i∈[1, nh]为样本中各像素的位置;k(x) 为核函数,h为核函数窗口宽度;b(xi) 为xi像素的方向编码索引映射,δ为狄拉克δ函数.
对每一帧,在各粒子的置信度计算过程中,为每个候选样本建立方向直方图,并计算每个候选样本与目标模板的相似度,以此作为粒子重要性的参考.各候选样本的方向直方图与目标模板的方向直方图之间的相似度采用巴氏系数来衡量.用ρ(y) 表示相似度,其计算公式为
| $ \rho \left( y \right) = \sum\limits_{k = 1}^n {\sqrt {{p_k}\left( y \right){p_k}\left( {{y_0}} \right)} } $ | (4) |
其中p(y) 和p(y0) 分别为候选样本和目标模板的方向直方图.
2.2 基于深度学习的特征提取在线下特征学习过程中,构建深度学习模型SDAE,并对从Tiny Images[5]数据集中随机选出的100万张图像进行训练,获得通用的图像高层特征.在跟踪过程中,首先初始化一个6层的神经网络,各层神经元的权重和相关参数由线下训练获得的特征决定.对第1帧,手动标出目标位置,采样得到目标模板和背景模板,并采用这些模板进行训练,得到适用于此视频序列的神经网络.为了使SoH-DLT方法进一步适应该特定视频序列,对第1帧完整的真实目标提取其SURF特征点集.
当新的1帧到来时,由于相邻帧的目标位置变化不会很大,所以提取当前帧在上一帧的SURF特征点集,并将第1帧的SURF特征点集与当前帧SURF特征点集进行匹配,得到匹配到的SURF特征点集.将匹配到的特征点在第1视频帧的位置映射到神经网络的输入层,则输入层神经元的激励函数为
| $ h = Z\left( {\left( {{\mathit{\boldsymbol{W}}_{\rm{o}}} + {\mathit{\boldsymbol{W}}_{\rm{s}}}} \right)x + b} \right) $ | (5) |
其中:h为输出,Z为sigmoid函数,x为输入数据,b为偏置;Wo为深度神经网络输入层权重矩阵,Ws为SURF特征点映射矩阵.当某一像素点为SURF特征点时,将该点权重设为0.3,反之,则设为0.与目标匹配度最高的粒子会获得更大的权重.因为SURF特征点具有尺度不变性,所以当目标存在尺度变化时,SoH-DLT方法也能获得稳定的跟踪效果.
2.3 粒子滤波跟踪算法对每一帧通过粒子滤波得到估计的目标粒子.通过在状态空间中传播随机变量来近似概率分布,根据之前的状态利用概率计算估计下一个最可能的状态.采用仿射变换参数来表示粒子状态.仿射变换参数是一个6维的向量,表示为
| $ \mathit{\boldsymbol{M}} = [x,y,{s_{\rm{c}}},{r_{\rm{o}}},{r_{\rm{a}}},{s_{\rm{a}}}] $ | (6) |
其中:x和y分别对应粒子样本中心点的纵坐标和横坐标,sc为粒子样本宽度与采样片宽度的比值,ro为粒子样本的旋转角度,ra为粒子样本高与宽的比值,sa为跟踪窗口的倾斜程度.
粒子滤波方法的一个主要思想是重要性重采样.首先,在当前帧以一定的规则放置许多粒子,如均匀放置,或者在靠近目标的地方多放置粒子,而远离目标的地方少放置粒子.然后,计算这些粒子与目标模板的相似度作为粒子权重,并进行归一化处理,使得所有粒子权重之和等于1.
在初始帧,n个粒子样本通过随机采样获得,且粒子权重都设为1/n.假设在t-1时刻,用{st-1i}i∈[1, n]表示n个粒子的状态,用{wt-1i}i∈[1, n]表示这些粒子对应的权重.重采样过程即从粒子集合中根据权重挑选n个粒子样本.首先,对权重集合{wit-1}i∈[1, n]计算归一化累计概率集合{cit-1}i∈[1, n]为
| $ c_{t - 1}^i = \frac{{\sum\limits_{k = 1}^i {w_{i - 1}^k} }}{{\sum\limits_{k = 1}^n {w_{i - 1}^k} }} $ | (7) |
随机生成n个在[0, 1]之间均匀分布的随机变量集合{ri}i∈[1, n].对ri,搜索{cit-1}i∈[1, n]获得含有n个最小索引的集合{Idxi}i∈[1, n],使得cIdxit-1≥ri.将st-1i替换为sIdxit-1,完成重采样过程.
粒子集合的更新通过系统状态变化方程来传播.当新的一帧到来时,即在t时刻,粒子状态集合为
| $ {s_t} = \mathit{\boldsymbol{A}}{s_{t - 1}} + {v_{t - 1}} $ | (8) |
其中:A为状态转移矩阵,vt-1为多元高斯随机变量,在此即为根据仿射变换参数生成的随机变量.
SoH-DLT方法采用2.2节中得到的神经网络进行粒子权重计算,每个粒子的置信度为
| $ E\left( y \right) = \rho \left( y \right)w\left( y \right) $ | (9) |
其中:E(y) 为粒子的置信度,ρ(y) 为该候选样本方向直方图与目标模板方向直方图之间的巴氏系数,w(y) 为通过神经网络计算获得的粒子权重.把置信度最大的粒子作为该帧的最终估计结果进行输出.通过这种方式,将候选样本的轮廓特征与细节特征结合起来进行考虑,使与目标最相似的候选样本成为估计的目标位置,提高了跟踪的准确度.
2.4 SoH-DLT方法步骤SoH-DLT方法的实现步骤如下.
1) 初始化:对第1帧f1采样,得到目标模板和背景模板,结合线下深度学习获得的高层特征训练得到神经网络nn;建立目标模板的方向直方图P,提取目标模板SURF特征点集S0.
2) 对于第i(i=2, 3, …, n) 帧fi:
a.采样粒子,获得候选样本集;
b.提取fi在fi-1目标位置的SURF特征点集Si,并进行匹配,得到SURF特征点映射矩阵Wsi,根据式(5) 更新nn输入层权重,并将粒子输入nn计算每个粒子的权重wi;
c.根据式(4) 计算每个候选样本与目标模板的相似度ρi;
d.根据式(9) 获得粒子置信度,置信度最大的粒子即为fi的目标位置.
3) 如果满足更新条件,重新采样目标与背景模板训练nn;如果不满足,则i=i+1,返回执行步骤2).
3 实验结果与分析对5个视频序列分别采用DFT[6]、IVT[7]、CT[8]、DLT[2]和所提方法SoH-DLT进行目标跟踪,以中心点误差和成功率来定量评价跟踪效果,并给出视觉上的效果评价.其中,IVT、DLT和SoH-DLT均采用仿射变换参数来表示样本状态.根据2.3节中对仿射变换的介绍,仿射变换参数的设置根据视频序列的特点而有所不同,会影响式(8) 中vt-1的取值,从而影响粒子集合的更新.为了使对比实验更有说服力,该3种跟踪方法的仿射变换参数均设为相同值.对Car4视频序列,目标尺度变化比较大,故仿射变换参数设为[4, 4, 0.02, 0, 0.001, 0];Car24和Man视频序列的尺度变化程度不大,故仿射变换参数设为[4, 4, 0.005, 0, 0.001, 0];在Deer视频序列中,目标运动迅速,相邻帧间目标位置变化较大,故仿射变换参数设为[12, 12, 0.005, 0, 0.001, 0],Surfer视频序列也存在目标快速运动的情况,但相邻帧间目标位置变化比Deer小,但尺度变化程度较大,故仿射变换参数设为[8, 8, 0.01, 0, 0.001, 0].此外,2.4节方法步骤3) 中的更新条件设置为粒子置信度小于0.8,或者距离上次神经网络更新已经超过50帧.
3.1 目标轮廓特征有效性分析SoH-DLT利用方向直方图对目标轮廓特征进行描述,将梯度方向分成36个区间.不同帧间目标与目标的方向直方图差距较小,即巴氏系数较大,而目标与背景的方向直方图差距较大,即巴氏系数较小.
在第1帧中手动标出目标位置,并建立目标模板的方向直方图.在粒子滤波跟踪过程中,计算每个粒子样本的方向直方图,并对每个粒子样本的方向直方图与目标模板的方向直方图计算巴氏系数,以此作为粒子重要性的参考.由于图像直方图变换易受光照影响,为了验证将方向直方图作为粒子重要性参考的可靠性,下面对Car4视频序列的第181帧到237帧进行了实验与分析,如图 2所示.在该段视频序列中,存在着明显的光照变化.每一帧的目标样本是由该帧目标真值得出的采样片,背景样本是在目标周围随机取样获得的采样片.
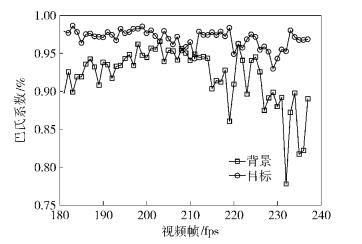
|
图 2 光照变化情况下不同样本与模板的相似性比较 |
由图 2可见,在光照变化情况下,目标样本方向直方图与目标模板方向直方图之间的巴氏系数总体上高于背景样本方向直方图与目标模板方向直方图之间的巴氏系数,即与目标模板相似的粒子可获得更高的置信度.有个别相差很小甚至相等的情况,对应于2.3节中的式(9) 中ρ(y) 相等,此时粒子的置信度完全依赖于神经网络计算得到的粒子权重w(y),即考虑采样粒子的细节特征.
为了更加直观地说明目标样本与背景样本的方向直方图之间的差别,抽取Car4视频序列中的第181帧和198帧,如图 3所示.待描述部分用黑色方框标出,每张图片右下角的直方图即为该张图片黑色方框区域的方向直方图.由图 3可以看出,不同帧之间的目标样本方向直方图相差不大,而目标样本与背景样本之间的方向直方图则有较大的差距.

|
图 3 目标与背景的方向直方图对比 |
采用2个客观指标来定量评价跟踪效果,即中心点误差和成功率.中心点误差是在某一帧用跟踪方法跟踪到的目标框中心点与该帧真实目标框的中心点之间的欧式距离,平均中心点误差则是一个视频序列每一帧的中心点误差之和除以其总帧数;对于某一帧,如果用跟踪方法跟踪到的目标框与真实目标框的重叠率大于50%,则认为该帧是成功跟踪的,成功率则是一个视频序列中成功跟踪到的帧数占总帧数的比例.
对5个视频序列采用不同跟踪方法进行跟踪的平均中心点误差和成功率如表 1所示.其中,第1个数字为成功率,括号里的数字为平均中心点误差. Car4和Car24视频序列的主要特点是存在明显的尺度和光照变化;Deer视频序列的主要特点是目标运动迅速且存在运动模糊;Surfer视频序列的主要特点是目标运动迅速和变形;Man视频序列的主要特点是明显的光照变化.由表 1可以看出,SoH-DLT方法对5个视频序列取得了最小的平均中心点误差和最大的平均成功率.其中,对Deer、Surfer和Man视频序列均取得了最小的平均中心点误差和最大的成功率;对Car4和Car24视频序列取得了最大的成功率和次小的中心点误差.总体而言,SoH-DLT方法与对比方法DFT、IVT、CT、DLT相比取得了更好的跟踪效果.
|
|
表 1 平均中心点误差和成功率对比 |
以Car4视频序列为例,对SoH-DLT和对比方法DFT、IVT、CT、DLT的跟踪效果进行分析. Car4视频序列是公路上的车辆行驶视频,被跟踪对象是汽车,在行驶过程中会发生明显的光照和尺度变化.其部分关键帧如图 4所示.

|
图 4 Car4视频序列各跟踪方法结果对比 |
在图 4中,第1列图片是视频序列的第181帧,此时的目标与第1帧相比尺寸减小,可见DFT和CT已经发生了漂移,而IVT、DLT和SoH-DLT能精确地跟踪到目标;第2列图片是第225帧,与第181帧相比,汽车的光照由亮变暗,SoH-DLT和IVT方法都成功地跟踪到目标,DLT虽然没有发生漂移但是覆盖率明显变小,CT和DFT更加偏离目标,跟踪失败;第3列图片是第233帧,目标光照由暗变亮,IVT和SoH-DLT都能较好地跟踪到目标,DLT的覆盖率依然是偏小的,而CT和DFT跟踪失败.
通过以上分析可以看出,SoH-DLT方法当目标有光照变化、尺度变化、形变和旋转时,与对比方法相比都能获得更好的跟踪效果.
4 结束语为了应对运动目标跟踪任务中存在的尺度、光照变化和形变等情况,笔者综合考虑运动目标的轮廓特征与细节特征,提出了基于混合特征的运动目标跟踪方法SoH-DLT.该方法利用方向直方图对尺度、光照变化和形变的不敏感性,充分描述候选样本的轮廓特征;将SURF特征与深度学习获得的高层特征相结合,并将其用于网络参数的修正.利用SURF特征的尺度不变性,该方法对尺度变化目标跟踪的成功率有了较大提高.
| [1] | Smeulders A W M, Chu D M, Cucchiara R, et al. Visual tracking:an experimental survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7): 1442–1468. doi: 10.1109/TPAMI.2013.230 |
| [2] | Wang Naiyan, Yeung Dityan. Learning a deep compact image representation for visual tracking[C]//Advances in Neural Information Processing Systems. Nevada:MIT Press, 2013:809-817. |
| [3] | Ma Chao, Huang Jiabin, Yang Xiaokang, et al. Hierarchical convolutional features for visual tracking[C]//International Conference on Computer Vision. Santiago:IEEE, 2015:3074-3082. |
| [4] | Vincent P, Larochelle H, Lajoie I, et al. Stacked denoising autoencoders:learning useful representations in a deep network with a local denoising criterion[J]. The Journal of Machine Learning Research, 2010, 11: 3371–3408. |
| [5] | Torralba A, Fergus R, Freeman W T. 80 million tiny images:a large data set for nonparametric object and scene recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(11): 1958–1970. doi: 10.1109/TPAMI.2008.128 |
| [6] | Sevilla-Lara L, Learned-Miller E. Distribution fields for tracking[C]//Computer Vision and Pattern Recognition. Providence:IEEE, 2012:1910-1917. |
| [7] | Ross D A, Lim Jongwoo, Lin Rueisung, et al. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2008, 77(1-3): 125–141. doi: 10.1007/s11263-007-0075-7 |
| [8] | Zhang Kaihua, Zhang Lei, Yang Minghsuan. Real-time compressive tracking[M]. Berlin Heidelberg: Springer, 2012: 864-877. |


