2. 盐城师范学院 信息工程学院, 江苏 盐城 224002
针对低功耗有损网络路由协议(RPL)能耗不均衡问题,提出一种能量有效的RPL多路径数据流分配算法.建立了一种更加符合实际的节点能量消耗模型,提出一种能量离散程度度量标准,以有效判定节点的能量均衡程度.基于该度量,提出一种快速求解算法,以获得数据的最优分发方案.实验结果表明,所提出的RPL多路径数据流分配算法均衡了节点的能量消耗,提高了路由的可靠性,延长了网络的生存时间.
2. School of Information Engineering, Yancheng Teachers University, Jiangsu Yancheng 224002, China
An energy-efficient multi-path routing protocol for low-power and lossy networks (RPL) distribution mechanism, energy-efficient routing protocol for low-power and lossy networks (EM-RPL), was proposed to solve the problem on imbalance of power consumption in RPL. Firstly, a model of node energy consumption was established, which is more in line with the actual node energy consumption. Secondly, an energy dispersion degree measurement criterion was presented. Based on this measure, a fast algorithm was proposed to obtain the optimal distribution of the data. Simulation results show that the improved RPL algorithm can balance the energy consumption of nodes, improve the reliability of routing, and prolong the lifetime of the network.
近年来,无线传感网在智能家庭、环境监控、智能建筑等诸多领域获得了广泛的应用.然而,这些网络因自身固有的特性导致拓扑结构不稳定且容易受到外部环境的干扰,使得链路质量随时间的变化而发生较大波动,因此如何构建有效的网络拓扑进行数据分发引起研究人员越来越多的关注.其中,面向低功耗有损网络的路由构建成为研究热点.为解决这一问题,国际互联网工程任务组(IETF,the Internet engineering task force) 的有损和低功耗网络路由(ROLL,routing over lossy and low-power networks) 工作组提出了低功耗有损网络路由协议(RPL,routing protocol for low-power and lossy networks)[1]. RPL协议是一种距离矢量路由协议.
1 研究背景为保证网络的可靠性,RPL允许一个节点拥有多个父节点,但只能有一个首选父节点,该节点的所有流量通过其首选父节点进行传输,其他父节点只作为备用.这使得首选父节点容易成为瓶颈节点,而当网络出现瓶颈节点后,这些节点的能量消耗速度明显加快,导致传感节点失效,出现网络黑洞,使网络失去连接性.因此,虽然RPL协议在一定程度上解决了低功耗有损网络的路由问题,但它并没有考虑各个节点间能耗均衡.为了保证网络质量,均衡节点的能量消耗是急待解决的问题.需要根据通信变化设计合理的数据转发方案.
当前,研究人员在这方面做了许多卓有成效的工作. Kamgueu等[2]关注网络的最小平均能量消耗,使用期望传输值(ETX,expected transmission count),根据链路的可靠性构建能量有效路由. Vasseur等[3]将能量来源分为3种:电力线供电、电池供电和能量拾取设备供电,根据对时间敏感度要求的不同使用不同的发射功率. Chang等[4]对RPL的可靠性和能量进行了分析,给出了网络的可靠性和能量度量,并在此基础上提出对节点剩余能量和ETX进行线性组合的方案. Iova等[5]使用期望生命周期表示剩余能量,通过对瓶颈节点的检测,根据剩余能量构建低功耗有损网络路由协议有向无环图(RPL DAG,routing protocol for low-power and lossy networks directed acyclic graph),在多个父节点中均衡负载. Le等[6]根据剩余能量和节点的使用频率构建目标函数,最大化节点的生命周期,延长网络的生存时间.然而,上述研究存在以下3个方面的不足:1) 将节点剩余能量作为度量标准之一,没有给出一个合理的能量消耗模型;2) 只能局部平衡能量消耗,没有考虑全局能耗的情况;3) 没有解决能量均衡的度量标准问题.
笔者通过构建符合实际的能量消耗模型,结合能量均衡的度量标准,提出一种快速求解算法以均衡节点的能量消耗,优化网络寿命.首先建立一种更加符合实际的节点能量消耗模型,然后提出一种有效判定节点的能量均衡程度的度量标准,随后提出一种快速求解算法,以获得数据的最优分发方案.实验结果表明,笔者方法均衡了网络节点的能量消耗,提高了路由可靠性.
2 能量有效的RPL多路径数据流分配算法笔者提出一种能量有效的RPL多路径数据流分配算法(EM-RPL,energy-efficient routing protocol for low-power and lossy networks).该方法通过评估网络中瓶颈节点能量消耗,实现整个网络的能量均衡,延长网络的生存时间.首先,分析了节点的基本能量消耗情况,然后根据“帕累托优”评价方案,给出节点能量分布均衡程度的度量,之后进一步分析基于多路径分配时节点能量消耗情况,最后给出流量分配的最优方案.
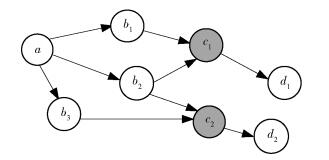
2.1 节点能量消耗模型以图 1所示的网络拓扑为例.其中,节点a为发送端,b1、b2和b3为其父节点,c1和c2为瓶颈节点.
|
图 1 节点的能量消耗 |
在处理数据的过程中,节点能耗可以分为3个部分,分别是新数据的接收能耗、计算能耗以及缓存队列的发送能耗.以节点c1为例,分别计算3个部分的能量消耗.
第1步 节点c1接收子节点发送的数据,其能量消耗主要是接收数据能耗,表示为
| $ {E_{{\rm{rce}}}}({c_1}) = \sum\limits_{P\left( b \right) = {c_1}} {\frac{{T(b,{c_1})}}{{R(b,{c_1})}}} \frac{{{E_{\rm{r}}}}}{{{D_{\rm{r}}}}} $ | (1) |
其中:P(b)=c1为所有以c1为父节点的集合,T(b, c1) 为节点b转发给c1的数据量,R(b, c1) 为节点b成功传给节点c1的数据分组比例,Er为每秒接收能耗,Dr为数据接收速率.
第2步 节点c1处理缓存队列,其计算能耗为
| $ {E_{{\rm{cmp}}}}({c_1}) = {N_{{\rm{task}}}}(B({c_1})){E_c} $ | (2) |
其中:Ntask为任务处理所需的指令周期,B(c1) 为节点c1的缓存使用量,Ec为每个指令周期处理能耗.
第3步 缓存队列处理完后,节点c1发送数据给其后继节点,能量消耗为
| $ {E_{{\rm{tat}}}}({c_1}) = \frac{{T({c_1},d)}}{{R({c_1},d)}}\frac{{{E_{\rm{t}}}}}{{{D_{\rm{d}}}}} $ | (3) |
其中:Et为每秒传输能耗,Dd为数据传输速率.
因此,节点c1的剩余能量为
| $ {E_{{\rm{rse}}}}({c_1}) = {E_{{\rm{crt}}}}({c_1}) - {E_{{\rm{tat}}}}({c_1}) - {E_{{\rm{cmp}}}}({c_1}) - {E_{{\rm{rce}}}}({c_1}) $ | (4) |
其中Erse(c1) 为节点c1在处理完所需要转发任务后的剩余能量.该度量值能影响瓶颈节点路由选择.
2.2 能量离散程度度量根据RPL协议,面向目标的有向无环图(DODAG,destination oriented directed acyclic graph) 一旦构建好路径后,所有流量会沿一条路径进行传输,直到网络拓扑发生变化为止.为了保证最大化网络生存时间,需要对DODAG进行改进,使其支持多路径,一个节点可将流量发给多个父节点而不是首选父节点.
实际上,无论选择哪个节点为首选父节点,瓶颈节点都要消耗能量.为了保证更有效地评价瓶颈节点是否能耗均衡,需要评估这些节点剩余能耗的离散程度.根据相关数学领域的知识,数据离散程度的评价一般使用极差、平均差、标准差等.然而,经过实验发现,这些方法无法有效描述出瓶颈节点的剩余能耗的分布情况.
为了准确评估瓶颈节点的能耗分布情况,基于帕累托优评价方案,给出能量分布均衡程度的度量.
能量离散程度定义:设有理数集合A={a1, a2, …, an},ai为传感器能量,且ai≥0,则能量离散程度(ED,energy of dispersion) 度量标准为
| $ M = \sum\limits_{i = 1}^n {{{\bar \omega }_i}a_i^2} $ | (5) |
其中:
为了验证ED的有效性,笔者对比了几种典型的评估离散程度的度量,包括极差、平均差和标准差.
通过数值实验来比较它们的差别.从[1, 100]间随机选取200个数,分别计算这些度量值.实验进行了1 000次并记录最大值、最小值和平均值.实验结果如表 1所示.
|
|
表 1 几种离散程度度量的对比结果 |
表 1显示,ED可很好地表示集合中数据的离散程度,能更加清楚地反映出数据集的波动情况.
2.3 基于多路径的能量消耗笔者使用多路径进行流量分配,主要考虑瓶颈节点的能耗.使用多路径路由时节点会通过不同质量的链路将数据包发给几个父节点,即通过几条路径传输流量,因此其能量消耗将依赖于发送到每一个父节点的流量.下面阐述如何在多路径环境下计算瓶颈节点的剩余能耗Erse.
如图 2所示,节点a为发送端,它的父节点为b1、b2和b3,瓶颈节点为c1和c2.对如图 2所示的流量进行分析,对节点c1来说,接收b1流量的100%和b2流量的20%.因此,c1的实际流量为30%+50%×20%.类似的,c2的实际流量为20%+50%×80%.

|
图 2 基于多路径的能量消耗 |
如果αx, y为节点x发送给其父节点y的流量比例,则瓶颈节点的流量为节点a分别发送给3个父节点的流量比率乘以它们转发给瓶颈节点的流量比率,并进行相应地叠加.更一般的表示为
| $ {\alpha _{a,c}} = \sum\limits_{b \in P\left( a \right)} {{\alpha _{a,b}}{\alpha _{b,c}}} $ | (6) |
通过将所有父节点到达瓶颈节点的比率相加,每个节点可通过递归的方式计算到达瓶颈节点的转发比率.因此瓶颈节点得到的实际流量为
| $ T\left( {a,c} \right) = \sum\limits_{b \in P\left( a \right)} {{\alpha _{a,b}}\frac{{T\left( {a,b} \right)}}{{R\left( {a,b} \right)}}} {\alpha _{b,c}}\frac{{T\left( {b,c} \right)}}{{R\left( {b,c} \right)}} $ | (7) |
由此,对瓶颈节点c1来说,式(1) 和式(3) 分别变为
| $ {E_{{\rm{rce}}}}({c_1}) = T(a,{c_1})\frac{{{E_{\rm{r}}}}}{{{D_{\rm{r}}}}} $ | (8) |
| $ {E_{{\rm{tat}}}}({c_1}) = \sum\limits_{d \in P({c_1})} {\frac{{{\alpha _{{c_1},d}}T({c_1},d)}}{{R({c_1},d)}}} \frac{{{E_{\rm{t}}}}}{{{D_{\rm{d}}}}} $ | (9) |
在这种情况下,瓶颈节点c1需消耗能量为
| $ \begin{array}{l} {E_{{\rm{rce}}}}({c_1}) + {E_{{\rm{cmp}}}}({c_1}) + {E_{{\rm{tat}}}}({c_1}) = T(a,{c_1})\frac{{{E_{\rm{r}}}}}{{{D_{\rm{r}}}}} + \\ {N_{{\rm{task}}}}(B({c_1})){E_{\rm{c}}} + \sum\limits_{d \in P({c_1})} {\frac{{{\alpha _{{c_1},d}}T({c_1},d)}}{{R({c_1},d)}}} \frac{{{E_{\rm{t}}}}}{{{D_{\rm{d}}}}} \end{array} $ | (10) |
其中除分配流量比例外,其余参数均可在数据传输前获得,因此通过节点a可评估出对瓶颈节点生存时间的影响.
2.4 基于多路径的流量分配构建多路径后,节点将在所有可用路径上分割流量,以保证每个瓶颈节点的生存时间均衡.为了最大化网络生存时间,可考虑使用线性求解程序为每个父节点分配权值以得到最优解.然而,这显然不适合存储和计算能力都受限的传感器节点.笔者基于使用的度量提出一种有效的流量分配算法.首先,将度量ED转化为关于αx, c的目标函数,即M=f(αx1, c1, αx2, c2, …),其中ci∈瓶颈节点集合,xi∈ci的子孙节点,这是二阶连续可微函数,可用线性规划的方法进行求解.然后,结合牛顿法和最速下降法,提出一种改进算法.笔者的目标函数为二阶连续可微函数和牛顿法的性质,因此该算法可收敛到全局最优.通过迭代测试,该算法可找出最好的一组权值来发送流量,同时它能尽快实现收敛,有很好的稳定性且计算量较少.下面的算法给出了它的形式化描述:节点判断是否得到合适的解(第1行),如果没有,则判断是否能进行精确搜索(第2行).如果可以,则搜索方向为
Algorithm: Energy balance based on multi-path
Input: object function f(αa, b1, αb, c2, …)
Output:〈αb, c1, αb, c2, …〉for energy balance
Initialization δ>0, αb, c=random [0, 1] and
1 for ‖∇f(xk)‖>δ
2 if
3
4 else
5 dk=-∇f(xk)
6 end
7
8 xk+1=xk+λkdk
9 k=k+1
10 end
11 return xk
该算法优点在于迭代步长调节采用精确搜索极小化二次函数的方法,收敛速度是线性的,且能保证每次∇f(xk) < 0.当∇2f(xk) 构成的Hessian矩阵的最大特征值和最小特征值相近时,下降速度最快.尤其是当它们相等时,经过一次迭代即可求出最优解.另外,随着网络的运行,瓶颈节点数量会逐渐变化.当瓶颈节点数量增加时,∇2f(xk) 的求解能耗增大.此时,可采用Quasi-Newton法减少Hessian矩阵的计算量,即
| $ \begin{array}{*{20}{c}} {{\nabla ^2}f({x_{k + 1}}) = {\nabla ^2}f({x_k}) + }\\ {{s_k}{{({s_k})}^{\rm{T}}}{{({s_k})}^{\rm{T}}}{y_k}1 + {{({y_k})}^{\rm{T}}}{\nabla ^2}f({x_k}){y_k}{{({s_k})}^{\rm{T}}}{y_k} - }\\ {\frac{1}{{{{({s_k})}^{\rm{T}}}{y_k}}}[{s_k}{{({y_k})}^{\rm{T}}} + {{({s_k})}^{\rm{T}}}{y_k}]{\nabla ^2}f({x_k})} \end{array} $ |
其中:sk=xk+1-xk,yk=∇f(xk+1)-∇f(xk).
3 实验及结果分析下面对算法性能进行评估,验证EM-RPL在不同网络规模、不同缓存大小情况下网络的负载分布、网络生存时间、能量消耗和路由稳定性等网络性能.
通过Contiki系统中的Cooja进行实验.在实验中,共使用了200个传感节点,随机分布在200 m×200 m的环境中,节点间的通信半径为10~20 m,汇聚节点放于中心位置,物理层和介质访问控制(MAC,media access control) 层使用IEEE 802.15.4,并采用CC2530节点的能耗参数和传输模型[7].为更好地说明问题,进行了多轮实验,并取平均值.
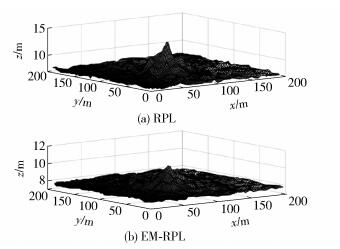
3.1 不同缓存容量的网络负载分布在实验中,设定每5 min发送1个数据包,sink节点位于网络中心.能量消耗情况如图 3和图 4所示,其中平面上的横、纵坐标表示实验区域(均为200 m),垂直坐标表示消耗的能量. 图 3(a)缓存大小为30 B,图 4(a)缓存大小为50 B.从图 3中可以看出,当节点越靠近sink端,其通信负载越大,这一现象表现为图中的中心部分相对突出,即消耗的能量较多.这符合传感网汇聚传输的特点,因为所有流量都流向汇聚节点,即sink节点.对图 3(a)和图 4(a)的比较还发现,当节点有较小的缓存容量,中心部分有更明显的尖峰.这是由于缓存较小时容易引起靠近中心的节点因缓存满而导致数据丢失,从而增加了数据重发的机率,消耗了更多的能量. 图 4(a)和图 4(b)表示,执行算法EM-RPL时不同缓存情况下的能量消耗情况.从图 4中可以看出,由于使用了能量均衡,使能量的分布更加均匀,网络的生存时间也会更长.这里无须考虑中心节点的能耗情况,因为中心节点一般使用电力供电而不使用电池供电.同时,该实验曲线较为平缓,这说明距离sink端同样距离的节点的负载大致相同,而RPL却难以保证这一点.
|
图 4 能量消耗分布对比(缓存为50) |
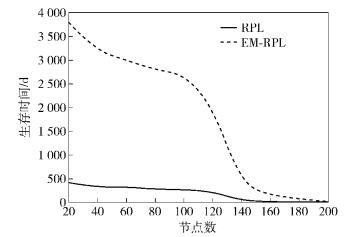
相应地,验证RPL和EM-RPL在不同网络规模下的最长生存时间.如图 5所示,EM-RPL可获得更长的生存时间.其中,数据包投递率(PDR,packet delivery ratio) 表示接收端接收到的数据包与发送端发送数据包的比值.尤其当网络规模不大时,这种优势更加明显.主要是因为EM-RPL能根据节点能量情况在不同的节点间均衡流量,特别是瓶颈节点的流量.但需注意的是,随着网络节点数增加,网络生存时间急骤下降,这是因为靠近sink端的节点必然要耗费大量的能量来转发数据.
|
图 5 不同网络规模的生存时间 |
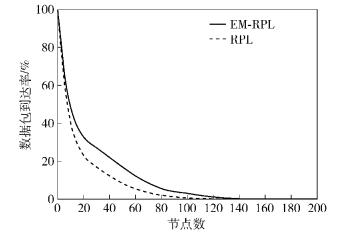
图 6所示为RPL和EM-RPL稳定性比较,从图 6中可以看出,RPL的稳定性较差,这是由于RPL都会频繁改变首选父节点从而导致网络的不稳定和过量的能量消耗.事实上,首选父节点的改变会触发定时器的重置,会引起更频繁的控制信息的传输.控制信息传输得越多,节点消耗的能量就越大.且频繁的改变会导致网络的不稳定,会使整个网络拓扑恶化.通过使用所有父节点参与流量转发,而不改变首选父节点,来保证网络稳定性.首选父节点只有在失效时才会改变,此时触发计时器才会重置.
|
图 6 不同网络规模的PDR |
在建立合理能量消耗模型的基础上,根据能量离散程度度量标准,通过快速求解算法,提出一种能量有效的RPL路由算法EM-RPL,以获得数据的最优分发方案.仿真结果表明,EM-RPL均衡了节点的能量消耗,提高了路由的可靠性,延长了网络的生存时间.下一步的工作将对汇聚节点周围的节点进行优化,以最大限度地延长它们的生存时间.
| [1] | Winter T, Thubert P, Brandt A, et al. RPL:IPv6 routing protocol for low-power and lossy networks[EB/OL]. (2012-03-10)[2016-03-16]. http://www.ietf.org/rfc/rfc6550.txt. |
| [2] | Kamgueu P O, Nataf E, Ndié T D, et al. Energy-based routing metric for RPL[J]. HAL-INRIA, 2013: 1–14. |
| [3] | Vasseur J P, Kim M, Pister K, et al. Routing metrics used for path calculation in low-power and lossy networks[EB/OL]. (2012-03-18)[2016-02-12]. http://www.ietf.org/rfc/rfc6551.txt. |
| [4] | Chang Linhuang, Lee Tsunghan, Chen Shujan, et al. Energy-efficient oriented routing algorithm in wireless sensor networks[C]//SMC 2013. Manchester:IEEE Press, 2013:3813-3818. |
| [5] | Iova O, Theoleyre F, Noel T. Using multiparent routing in RPL to increase the stability and the lifetime of the network[J]. Ad Hoc Networks, 2015, 29: 45–62. doi: 10.1016/j.adhoc.2015.01.020 |
| [6] | Le Quan, Ngo-Quynh T, Magedanz T. RPL-based multipath routing protocols for internet of things on wireless sensor networks[C]//ATC 2014. Hanoi:IEEE Press, 2014:424-429. |
| [7] | Ti. CC2530 data sheet[EB/OL]. (2014-04-07)[2016-04-05]. http://www.ti.com.cn/product/cn/cc2530. |


