2. 天津市智能机器人技术重点实验室, 天津 300350;
3. 中国民航大学 理学院, 天津 300300;
4. 哈尔滨工程大学 自动化学院, 哈尔滨 150001
基于矩阵半张量积(STP)方法研究了一类Petri网系统(PNSs)的建模和可达性问题.首先,利用STP将这类PNSs的动态演化表示为离散时间双线性方程;然后,给出了这类PNSs的变迁-状态邻接矩阵的定义,利用所建立的双线性方程和变迁-状态邻接矩阵给出了这类PNSs状态可达性判别的几个充要条件,同时设计了计算这类PNSs任意两可达状态的所有路径的有效算法;最后,用实例说明了所得结果的可行性与有效性.
2. Tianjin Key Laboratory of Intelligent Robotics, Nankai University, Tianjin 300350, China;
3. College of Science, Civil Aviation University of China, Tianjin 300300, China;
4. College of Automation, Harbin Engineering University, Harbin 150001, China
Modeling and reachability of a class of Petri net systems (PNSs) by using the semi-tensor product of matrices (STP) was investigated. First, the dynamics of PNSs, by resorting to STP, are converted into a discrete-time bilinear equation. Second, the transition-state adjacency matrix of the PNSs is defined, several necessary and sufficient conditions are obtained for the reachability of the PNSs by means of this bilinear equation and transition-state adjacency matrix. A new algorithm is also designed to find all of the firing sequences of any two reachable states. Finally, an example is presented to illustrate the theoretical results.
可达性是Petri网系统(PNSs, Petri net systems) 最重要的动态性质,它直接反映了PNSs的运行情况.而且,PNSs的其余各种动态性质都可通过可达性来定义,如活性、公平性、持续性和可逆性等[1].因此,可达性判别问题是PNSs理论研究中最重要课题之一.众所周知,对于普通PNSs来说,传统的状态方程存在非负整数解只是PNSs状态可达的一个必要条件.据笔者所知,至今仍然是一个未解决的问题.然而,对某些PNSs子类,传统的状态方程存在非负整数解不仅是状态可达的一个必要条件,也是充分条件.如Tsuji等[2]讨论了无有向回路PNSs可达性问题,Kumagai等[3]讨论了一类标识图可达性问题,吴哲辉[4]讨论了活的标识T-图与活的加权T-系统可达性问题,等等.笔者所讨论的这类PNSs是最常见、应用最广泛的一类PNSs[5],它的可达性问题目前只有基于传统状态方程的判别方法,且只是一个必要非充分条件.因此,研究这类PNSs的可达性问题,具有理论和实践意义.
笔者首次利用矩阵的半张量积(STP, the semi-tensor product of matrices) 方法研究了这类PNSs状态可达性问题.首先,利用STP方法建立了这类PNSs的状态演化的离散时间双线性方程.该方程的优点不仅在于它包含状态和变迁的全部信息,而且该方程的变迁-状态转移矩阵对PNSs的可达性分析至关重要.其次,给出了这类PNSs的变迁-状态邻接矩阵的定义,并利用变迁-状态邻接矩阵和状态演化方程给出了这类PNSs状态可达性判别的几个充要条件.同时,给出了这类PNSs任意2个可达状态之间的可达路径计算公式.
1 预备知识 1.1 所用到的一些符号及其说明① Mm×n表示m×n实矩阵构成的集合.
② M(i, j)表示矩阵M的第i行、第j列元素.
③ Colj(M) 表示矩阵M的第j列.
④ Col (M) 表示矩阵M的列构成的集合.
⑤ 1n=
⑥ δn0=
⑦ Δn={δn1, δn2, …, δnn},其中δnk表示单位矩阵In的第k列,1≤k≤n.
⑧ L=[δmi1, δmi2, …, δmin]简记为L=δm[i1, i2, …, in],其中ik∈{0, 1, 2, …, n}.
⑨ Blki(A) 表示矩阵A∈Mn×mn第i个n×n块矩阵,1≤i≤m,即A=[Blk1(A), …, Blkm(A)].
⑩ ℕ+表示正整数构成的集合.
⑪ ℕn={α|α=(a1, …, an)T, ai∈ℕ, i=1, 2, …, n}.
⑫ ℝn表示实数域上n维列向量的集合.
⑬
这里只介绍所用到STP的一些内容,有关STP更详细介绍见文献[6].
定义1[6] 设矩阵A∈Mm×n,B∈Mp×q,则称(A⊗It/n)(B⊗It/p) 为A与B的半张量积.即
| $ \mathit{\boldsymbol{A}} \times \mathit{\boldsymbol{B}} = (\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{I}}_{t/n}})(\mathit{\boldsymbol{B}} \otimes {\mathit{\boldsymbol{I}}_{t/p}}) $ | (1) |
其中:t=LCM (n, p) 为n与p最小公倍数,⊗为矩阵的Kronecker积.
注:当n=p时,(1) 式变为A×B=AB,即STP是普通矩阵乘积的推广.因此,在不导致混淆的情况下,略去符号“×”.
定义2[6] 一个换位矩阵W[m, n]是一个mn×mn矩阵,其定义如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{[m,n]}} = {\mathit{\boldsymbol{\delta }}_{mn}}[1,m + 1,2m + 1, \cdots ,\left( {n - 1} \right)m + 1,}\\ {2,m + 2,2m + 2, \ldots ,\left( {n - 1} \right)m + 2, \ldots ,m,2m, \ldots ,nm]} \end{array} $ | (2) |
引理1[6]设X∈ℝm, Y∈ℝn, 则
| $ {\mathit{\boldsymbol{W}}_{[m,n]}}\mathit{\boldsymbol{XY}} = \mathit{\boldsymbol{YX}},{\mathit{\boldsymbol{W}}_{[n,m]}}\mathit{\boldsymbol{YX}} = \mathit{\boldsymbol{XY}} $ | (3) |
下面只介绍所用到PNSs的一些概念,有关PNSs更全面的介绍见文献[1, 4].
定义3[1] 一个加权PNSs是一个5元组N=(P, T, F, W, M1),其中P={p1, p2, …, pn}为有限库所集合,T={t1, t2, …, tm}为有限变迁集合,F⊆(P×T)∪(T×P) 为弧/流关系集合,W:F→{1, 2, …}为权函数,M1:P→{0, 1, 2, …}为初始状态\初始标识,P∩T=∅且P∪T≠Φ.
注:如果W:F→{1}(权函数的函数值恒1),称N=(P, T, F, W, M1) 为普通PNSs,并简记为N=(P, T, F, M1).因为普通PNSs与加权PNSs有相同的模拟能力,二者不同的只是建模的效率和方便性.所以,只讨论原型PNSs.
定义4[4] 一个PNSs具有如下变迁发生规则:
1) 对于变迁,若
| $ \forall p \in P:p \in {}^ \bullet t \to M\left( p \right) \ge 1 $ |
则称变迁t在标识M有发生权,记为M[t>.
2) 设M[t>,则标识M发生变迁t得到一个新的标识M′(记为M[t>M′) 且有
| $ M\prime \left( p \right) = \left\{ \begin{array}{l} M\left( p \right) - 1,p \in {}^ \bullet t - {t^ \bullet }\\ M\left( p \right) + 1,p \in {t^ \bullet } - {}^ \bullet t\\ M\left( p \right),其他 \end{array} \right. $ | (4) |
其中•t和t•分别表示变迁t的输入库所集和输出库所集.
2 PNSs的矩阵表示本节讨论一类PNSs动态演化的矩阵表示.考虑N=(P, T, F, M1),其中∀t∈T:|•t|=|t•|=1.有的文献将这类PNSs称为标识S-图或状态机.下面所提及的网系统均为这类PNSs.
在这类PNSs中,由于每个变迁的发生恰有一个库所减少一个标识而另一个库所增加一个标识.因此,由定义4不难得出如下引理.
引理2 设PNSs N=(P, T, F, M1) 的初始状态为M1=[x1, x2, …, xn]T,
| $ \sum\limits_{i = 1}^n {{x_i}} = \sum\limits_{i = 1}^n {{{\tilde x}_i}} $ | (5) |
由引理2可知,一旦N=(P, T, F, M1) 的初始状态确定,则这类PNSs就是有界的,即有有限个状态.其全部可能的状态数可通过如下引理得到.
引理3 设n维整数列向量α=[x1, x2, …, xn]T,且满足
| $ s = C_{n + k - 1}^{n - 1} $ | (6) |
众所周知,PNSs的状态个数随着库所、变迁和标识数增加呈指数增长,进而导致所谓的“状态空间爆炸”问题,这是PNSs的致命缺点.但由引理2和引理3可知,所讨论的这类PNSs的状态个数最多为s=Cn+k-1n-1,其中n为库所个数,k为库所中标识总数.这是一个多项式时间增长的,而不是指数增长的.这就是此类PNSs在实际系统中被广泛应用的原因所在.
下面,考虑这类PNSs状态方程的矩阵表示.对于N=(P, T, F, M1),其中∀t∈T:|•t|=|t•|=1.初始状态M1=[x1, x2, …, xn]T满足
用x(t) 表示t步时状态的向量形式,x(t)=δs0表示前一时刻的状态在相应变迁下不能发生;u(t) 表示t步时变迁的向量形式.由定义4可知,第t+1步时的状态由第t步时状态和第t步时的使能变迁决定.因此,有
| $ \mathit{\boldsymbol{x}}\left( {t + 1} \right) = f\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right)} \right) $ | (7) |
利用STP可以将式(7) 转化为离散时间双线性系统,即有如下定理.
定理1 设PNSs N=(P, T, F, M1) 满足∀t∈T:|•t|=|t•|=1,则N的动态演化可等价表示为
| $ \mathit{\boldsymbol{x}}\left( {t + 1} \right) = \mathit{\boldsymbol{Lu}}\left( t \right)\mathit{\boldsymbol{x}}\left( t \right) $ | (8) |
其中:L∈Ls×sm称为N的变迁-状态转移矩阵,s=Cn+k-1n-1,n为N库所的个数,k为N中各库所标识数之和.
3 PNSs的可达性分析下面讨论这类PNSs的可达性问题.首先,给出这类PNSs可达性定义.
定义5[4] 设PNSs N=(P, T, F, M1) 满足∀t∈T:|•t|=|t•|=1.若∃t∈T,使得M[t>M′,则称状态M′是从状态M直接可达的.如果存在变迁序列t1t2…tk-1和状态序列M1M2…Mk使得
| $ {\mathit{\boldsymbol{M}}_1}[{t_1} > {\mathit{\boldsymbol{M}}_2}[{t_2} > {\mathit{\boldsymbol{M}}_3} \cdots {\mathit{\boldsymbol{M}}_{k - 1}}[{t_{k - 1}} > {\mathit{\boldsymbol{M}}_k} $ | (9) |
称状态Mk是从状态M1经过t-1步可达的.
方便起见,记变迁序列σ=t1t2…tk∈T*,则(9) 式可简记为M1[σ>Mk.
引理4[6] 设∝j=1tδmj=δmti,则δmj=Sj, mt∝δmti,j=1, 2, …, t.其中:
| $ \left. \begin{array}{l} {S^t}_{1,m} = {I_m} \otimes {1_{{m^{t - 1}}}}\\ {S^t}_{2,m} = \underbrace {[{I_m} \otimes {1_{{m^{t - 2}}}}, \cdots ,{I_m} \otimes {1_{{m^{t - 2}}}}]}_m\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {S^t}_{t - 1,m} = \underbrace {[{I_m} \otimes {1_m}, \cdots ,{I_m} \otimes {1_m}]}_{{m^{t - 2}}}\\ {S^t}_{t,m} = \underbrace {[{I_m}, \cdots ,{I_m}]}_{{m^{t - 1}}} \end{array} \right\} $ | (10) |
定理2 设PNSsN=(P, T, F, M1) 的状态演化方程如式(8) 所示. x1=x(1)=δs1为初始状态,xd=δsd为目标状态,则xd是从x1经t步可达的当且仅当∃i∈{1, 2, …, mt},使得
| $ {\mathit{\boldsymbol{x}}_d} = {\rm{Co}}{{\rm{l}}_i}({(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[s,m]}})^t}{\mathit{\boldsymbol{x}}_1}) $ | (11) |
且可达路径可由引理4中δmti=ti1ti2…tit得到.
证明 由式(8) 可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {t + 1} \right) = \mathit{\boldsymbol{Lu}}\left( t \right)\mathit{\boldsymbol{x}}\left( t \right) = \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[s,m]}}\mathit{\boldsymbol{x}}\left( t \right)\mathit{\boldsymbol{u}}\left( t \right) = }\\ {{{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[s,m]}})}^2}\mathit{\boldsymbol{x}}\left( {t - 1} \right)\mathit{\boldsymbol{u}}\left( {t - 1} \right)\mathit{\boldsymbol{u}}\left( t \right) \cdots = }\\ {{{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[s,m]}})}^t}\mathit{\boldsymbol{x}}\left( 1 \right)\mathit{\boldsymbol{u}}\left( 1 \right)\mathit{\boldsymbol{u}}\left( 2 \right) \cdots \mathit{\boldsymbol{u}}\left( t \right) = }\\ {({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[s,m]}})}^t}{\mathit{\boldsymbol{x}}_1}){ \propto ^t}_{j = 1}\mathit{\boldsymbol{u}}\left( j \right)} \end{array} $ | (12) |
必要性:若xd是从x1经t步可达的,则存在使能变迁序列u(1)u(2)…u(t),使得式(12) 成立.因此,xd∈Col ((LW[s, m])tx1).于是存在i∈{1, 2, …, mt},使得xd=Coli((LW[s, m])tx1).此外,由引理4容易得到可达路径δimt=ti1ti2…tit.
充分性:若存在i∈{1, 2, …, mt},使得式(11) 成立,则存在使能变迁序列∝j=1tu(j)=δmti,使得式(12) 成立,即xd=((LW[s, m])tx1)∝j=1tu(j).因此,状态xd是从x1经t步可达的.
证毕.
推论1 PNSsN=(P, T, F, M1) 的状态xd=δsd是从x1=δs1可达的当且仅当存在正整数k≤s,使得
| $ {\mathit{\boldsymbol{x}}_d} \in \left\{ {\bigcup\limits_{t = 1}^k {{\rm{Col}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[s,m]}})}^t}{\mathit{\boldsymbol{x}}_1})} } \right\} $ |
其中s为N的状态个数.
下面给出PNSs的变迁-状态邻接矩阵定义,然后利用所定义的变迁-状态邻接矩阵讨论PNSs状态可达性问题.
定义6 设PNSsN=(P, T, F, M1) 的状态集为S={M1, M2, …, Ms}.称A=(aij)s×s为N的变迁-状态邻接矩阵,其中:
| $ {a_{ij}} = \left\{ \begin{array}{l} 1,\exists {t_k} \in T,s.t.{\mathit{\boldsymbol{M}}_j}[t > {\mathit{\boldsymbol{M}}_i}\\ 0,其他 \end{array} \right. $ |
由定义6容易得到定理3.
定理3 设PNSsN=(P, T, F, M1),矩阵A=(aij)s×s为其变迁-状态邻接矩阵,且假设At=(aijt)s×s, A1=A,则状态Mi是从状态Mj经t步可达的当且仅当aijt>0.此外,若aijt=c≠0,则从状态Mj经t步到达状态Mi有c条路径.
为了得到PNSs的变迁-状态转移矩阵L和变迁-状态邻接矩阵A的关系,首先将Petri网N的变迁-状态转移矩阵L∈Ls×sm做如下分解:
| $ \mathit{\boldsymbol{L}} = ({\rm{Bl}}{{\rm{k}}_1}\left( \mathit{\boldsymbol{L}} \right),{\rm{Bl}}{{\rm{k}}_2}\left( \mathit{\boldsymbol{L}} \right), \cdots ,{\rm{Bl}}{{\rm{k}}_m}\left( \mathit{\boldsymbol{L}} \right)) $ | (13) |
其中Blkl(L)∈Ms×s为矩阵L的第l块(1≤l≤m).于是,有如下命题.
命题1 设PNSsN=(P, T, F, M1) 的变迁-状态转移矩阵如式(13) 所示,变迁-状态邻接矩阵A如定义6所示,则
| $ \mathit{\boldsymbol{A}} = \sum\limits_{l = 1}^m {Bl{k_l}\left( \mathit{\boldsymbol{L}} \right)} $ | (14) |
定理3表明,{At|t=1, 2, …}包含了PNSsN状态可达性的全部信息.由代数学中的Cayley-Hamilton定理[7]可知,若(At)(i, j)=0, ∀t≤s,则(At)(i, j)=0,∀t=1, 2, ….因此,只需考虑{At|t≤s}即可.
由定义6、定理3和命题1可得出如下结论.
定理4 设PNSsN=(P, T, F, M1) 的状态演化方程如式(8) 所示,S={M1, M2, …, Ms}为其状态集,则:
1) 状态Mi是从状态Mj经t步可达的当且仅当
| $ {\left( {{{\left( {\sum\limits_{l = 1}^m {{\rm{Bl}}{{\rm{k}}_l}\left( \mathit{\boldsymbol{L}} \right)} } \right)}^t}} \right)_{\left( {i,j} \right)}} > 0 $ |
2) 状态Mi是从状态Mj可达的当且仅当存在正整数k(k≤s) 使得
| $ \sum\limits_{t = 1}^k {{{\left( {{{\left( {\sum\limits_{l = 1}^m {{\rm{Bl}}{{\rm{k}}_l}\left( \mathit{\boldsymbol{L}} \right)} } \right)}^t}} \right)}_{\left( {i,j} \right)}} > 0} $ |
例1 讨论图 1所示PNSs的可达性问题.
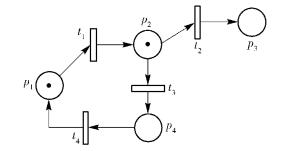
|
图 1 例1所示的PNSs |
由定义4可知,此PNSs的状态转移图如图 2所示.
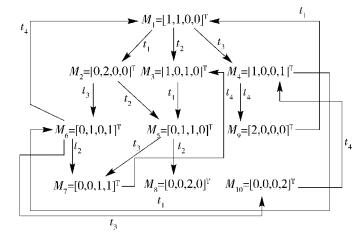
|
图 2 摇例1所示PNSs的状态转移图 |
设此Petri网的状态集S={M1, M2, …, M10}, 变迁集T={t1, t2, t3, t4}.为了得到其状态演化动态方程,将此Petri网状态和变迁分别表示成向量形式,即δi10~Mi(1≤i≤10),δj4~tj(1≤j≤4),则状态集和变迁集的向量形式分别为Δ10={δ101, δ102, …, δ1010},Δ4={δ41, δ42, δ43, δ44}.借助于STP,此PNSs的状态演化可表示为
| $ \mathit{\boldsymbol{x}}\left( {t + 1} \right) = \mathit{\boldsymbol{Lu}}\left( t \right)\mathit{\boldsymbol{x}}\left( t \right) $ |
其中变迁-状态转移矩阵为
| $ \begin{array}{l} \mathit{\boldsymbol{L}} = {\mathit{\boldsymbol{\delta }}_{10}}[2,0,5,6,0,0,0,0,1,0,3,5,0,0,8,7,0,0,0,\\ 0,4,6,0,0,7,10,0,0,0,0,0,0,0,9,0,1,3,0,0,4] \end{array} $ |
利用定理2,讨论此PNSs的可达性问题.为节省篇幅,仅讨论t=3时的情况.
当t=3时,有
| $ \begin{array}{*{20}{c}} {{\rm{Co}}{{\rm{l}}_{12}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = {\rm{Co}}{{\rm{l}}_{36}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = }\\ {{\rm{Co}}{{\rm{l}}_{45}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = \mathit{\boldsymbol{\delta }}_{10}^1}\\ {{\rm{Co}}{{\rm{l}}_7}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = {\rm{Co}}{{\rm{l}}_{10}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = }\\ {{\rm{Co}}{{\rm{l}}_{19}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}){\rm{ }} = {\rm{Co}}{{\rm{l}}_{34}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = \mathit{\boldsymbol{\delta }}_{10}^7}\\ {{\rm{Co}}{{\rm{l}}_6}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = {\rm{Co}}{{\rm{l}}_{18}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = \mathit{\boldsymbol{\delta }}_{10}^8}\\ {{\rm{Co}}{{\rm{l}}_{11}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = {\rm{Co}}{{\rm{l}}_{35}}({{(\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{[10,4]}})}^3}{\mathit{\boldsymbol{x}}_1}) = \mathit{\boldsymbol{\delta }}_{10}^{10}} \end{array} $ |
其余各列均为零.由定理2可知,状态M1、M7、M8、M10是从初始状态M1经3步可达的.例如,对于状态M7,其可达路径为δ647=δ41δ42δ43~t1t2t3,δ6410=δ41δ43δ42~t1t3t2,δ6419=δ42δ41δ43~t2t1t3,δ6434=δ43δ41δ43~t3t1t2.
作为所得结果的一个简单应用,研究了这类PNSs的可逆性问题.
由文献[1]可知,PNSsN=(P, T, F, M1) 是可逆的网系统当且仅当∀M∈R(N, M1),总有M1∈R(N, M) 成立.换句话说,N=(P, T, F, M1) 是可逆的网系统当且仅当它的任意两状态都是互相可达的.
为此,考虑状态M1和M8.对任意正整数t,经简单计算有Col (LW[10, 4])tδ108={δ100}成立,因此δ101∉Col (LW[10, 4])tδ108.由定理2可知,状态M8不能达到状态M1.因此,例1所示的Petri网是不可逆的网系统.
注:实例的数值计算是通过Matlab的STP工具箱完成的.关于STP数值计算的详细介绍见网址http://lsc.amss.ac.cn/~simdcheng/stp/STP.zip.
5 结束语基于STP方法研究了一类PNSs建模和可达性问题.首先,利用STP方法建立了这类PNSs的动态演化方程;其次,利用PNSs的变迁-状态邻接矩阵和变迁-状态转移矩阵给出了其状态可达性判别的几个充要条件,与此同时也给出了任意2个可达状态之间的可达路径的计算公式;最后,实例说明了所得到结果的可行性和有效性.
未来的工作将集中在以下几方面:①利用所建立的数学框架研究此类PNSs的其他控制问题,如可控性、可观测性及稳定性等问题;②将所得到的结果推广到更一般的PNSs中.
| [1] | Murata T. Petri nets:properties, analysis and applications[J]. Proceedings of the IEEE, 1989, 77(4): 541–580. doi: 10.1109/5.24143 |
| [2] | Tsuji K, Murata T. On reachability conditions for unrestricted Petri nets[C]//IEEE International Symposium on Circuits and Systems. Chicago:[s. n.], 1993:2713-2716. http://dblp.uni-trier.de/db/conf/iscas/iscas1993-4 |
| [3] | Kumagai S, Kodama S, Kitagawa M. Submarking reachability of marked graphs[J]. IEEE Transactions on Circuits and Systems, 1984, 31(2): 159–164. doi: 10.1109/TCS.1984.1085479 |
| [4] | 吴哲辉. Petri网导论[M]. 北京: 机械工业出版社, 2006. |
| [5] | Peterson J. Petri Nets[J]. Computing Surveys, 1977, 9(3): 223–252. doi: 10.1145/356698.356702 |
| [6] | Cheng Daizhan, Qi Hongsheng, Zhao Yin. An introduction to semi-tensor product of matrices and its applications[M]. Singapore: World Scientific, 2012. |
| [7] | Gradshteyn S, Ryzhik M. Tables of integrals, series, and products[M]. Sixth Edition. San Diego: Academic Press, 2000. |


