2. 金陵科技学院 电子信息工程学院, 南京 211169;
3. 金陵科技学院 软件工程学院, 南京 211169
提出了基于信源编码技术的无线传感器网络可恢复数据融合隐私保护方案.借助于节点数据相关性对隐私数据进行信源编码,实现了数据隐藏和压缩,对编码后的数据进行了形式转换和拼接,以进行原始数据的恢复,同时利用聚合签名技术鉴别数据的完整性.实验结果表明,该方案能在有效保护数据隐私性、减少数据传输量的基础上,实现对原始感知数据的恢复.
2. School of Electrical and Information Engineering, Jinling Institute of Technology, Nanjing 211169;
3. School of Software Engineering, Jinling Institute of Technology, Nanjing 211169
Based on source coding technology, recoverable privacy-preserving data aggregation scheme for wireless sensor networks was proposed. The sensor data is hidden and compressed by source coding technology according to the correlation between them. Secondly, the coded data is converted and concatenated so that the base station can recover it. Meanwhile, the base station verified the integrity of data in accordance with aggregate signature. Experiment results demonstrate that the proposed scheme can realize the recovery of original data on the basis of protecting data privacy as well as decreasing redundant transmitted data.
数据融合是解决无线传感器网络资源受限问题的核心技术之一.在这一领域中,如何实现数据的隐私保护以及如何在此同时实现数据在基站节点的恢复,是亟须解决的2个难点问题.目前,已经有很多研究者提出了可恢复数据融合隐私保护的方法[1-5].总体来说,现有方法均存在一定的不足,如椭圆加密算法很大程度上增加了节点的运算开销,分片技术显著增加了网络中数据的传输量,直方图技术则以牺牲融合精度为代价,这对于能量和计算能力受限的无线传感器网络来说无疑是不适用的.笔者针对现有方案存在的问题,通过信源编码技术对原始数据进行压缩以降低通信量,且在不需要加密的前提下对数据进行隐藏,借助于聚合签名实现数据的完整性验证,实现了一种轻量级的可恢复数据融合隐私保护方案.
1 背景知识 1.1 分布式信源编码分布式信源编码是建立在Slepian-Wolf定理基础之上的一种方法,用来解决若干个互不通信的信源之间的数据压缩问题.该编解码方案不需要与边信息节点通信,因此可减少通信能耗,保护数据的隐私性.为了降低信源编码带来的额外开销,笔者采用了轻量级的分布式信源编码方式,即模制编码[6],其编解码过程如下.
对于某个监测场景,假设其感知数据大小范围为[min s, max s],采集样本间的最小距离(即监测精度) 为Δ,若样本数据的长度为n-bit,则样本空间可表示为集合
| $ \mathit{\Omega }{\rm{ = }}\left\{ {{d_i}\left| {{d_i} = \min s + i\Delta ,i \in \left( {0,1, \cdots ,{2^n} - 1} \right)} \right.} \right\} $ |
对于2个相关数据di和dj,若
| $ |{d_i} - {d_j}| < {2^{k - 1}}\Delta ,0 \le k \le n $ |
根据模值编码,可对di进行k-bit长度的编码为
| $ {m_i} = E({d_i}) = I({d_i}){\rm{mod}}{2^k} $ | (1) |
其中:E(di) 为di的编码,I(di) 为di在样本空间集合Ω中的编号.将样本空间集合中编码后相同的元素定义为一个陪集,可知陪集的数量为2k个,记为
| $ {S_{\underbrace {0 \ldots 0}_k}},{S_{\underbrace {0 \ldots 1}_k}}, \cdots ,{S_{\underbrace {1 \ldots 1}_k}} $ |
则节点i所在的陪集下标即为数据di的编码结果.译码端可根据节点i的数据编码E(di) 和其参照编码的边数据dj恢复出实际的数据为
| $ {m_i} = D({c_i}) = \mathop {{\rm{min}}}\limits_{{d_n} \in S} \left\| {{d_j} - {d_n}} \right\| $ | (2) |
其中:D(ci) 为ci的译码,S为数据di所在的陪集,dn为该陪集中的元素.由于模值编码过程只需要通过简单的数值计算即可得出编码结果,其复杂度为O(1).
1.2 聚合签名聚合签名(AS,aggregate signature) 是一种支持聚合特性的数字签名变体[7],即给定n个用户为
| $ {u_i} \in U,{\rm{ }}1 \le i \le n $ |
其中U为用户集合,对n个消息有
| $ {m_i} \in M\left( {1 \le i \le n} \right) $ |
其中:M为消息集合的n个体签名,聚合签名的生成者可将这n个单一签名聚合成1个唯一的短签名σ,如签名(σ1, σ2) 可聚合成σ12,随后也可和σ3继续聚合成σ123.
2 网络模型首先,对于传感器网络G=(V, E),V为网络中全体节点的集合,共有N节点随机、均匀地分布在一个L×L的2维区域内,其中仅有1个基站节点Sink位于网络的拓扑中心.
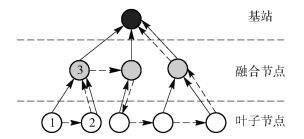
假设已经建立起了树形结构的融合树T,则节点可以分为3种类型:叶子节点、中间融合节点和根节点基站,如图 1所示实线箭头结构.
|
图 1 拓扑结构与编码关系示意图 |
相关定义如下.
定义1 编码链表C-link:用以描述节点间的编码关系的一个单向编码链,编码起始节点为表头节点,基站为表尾节点,链表中任意一个节点以其后继节点为边信息进行编码.
如图 1所示,虚线箭头表示的则为编码链表,节点1以节点2为边信息进行信源相关编码,记为
| $ S({n_1}) = {n_1}.{\rm{next}} = {n_2} $ |
定义2 解码链表D-link:编码链表的反向链表,用以描述节点间的解码关系的一个单向编码链,表头节点为基站节点.
3 算法描述笔者在文献[1]的基础上,引入了信源编码技术,提出一种轻量级可恢复数据融合隐私保护方案,其算法流程包括4个基本阶段.
步骤1 初始化阶段
1) 对于每一个节点i,生成一个密钥对(PKi=vi, SKi=xi)
2) 随机选择T中的叶子结点,选择距离其最近的节点作为其后继节点,直至所有节点均加入该链表,最终生成编码链表C-link及其反向链表D-link.
步骤2 编码与签名
终端节点ni收集到原始数据后,执行操作如下:
1) 根据节点ni与ni.next节点数据的相关性,执行式(2),计算数据di的编码信息mi.
2) 为了实现数据的可恢复性,节点在实现信源编码后仍需要对数据的形式做出变换为
| $ {c_i} = {m_i}\left\| {{0^\beta },\beta = l\left( {i - 1} \right)} \right. $ | (3) |
其中:l为能表示网络中所有传感器节点采集原始数据mi的最小bit长度,再根据节点序号i在有效数据bit后附加β=l(i-1) 个0.
3) 签名:σi=xiH(mi).
步骤3 数据融合与聚合签名
融合节点接收到t个子节点传输的数据包(c1, σ1), (c2, σ2), …, (ct, σt),对数据部分进行计算为
| $ {c_{{\rm{agg}}}} = \sum\limits_{i = 1}^t {{c_i}} = \sum\limits_{i = 1}^t {{m_i}\left\| {{0^{l(i - 1)}}} \right.} $ | (4) |
对于接收到的t个数据的签名,进行聚合操作为
| $ {\sigma _{{\rm{agg}}}} = \sum\limits_{i = 1}^t {{\sigma _i}} $ | (5) |
然后,将中间融合结果及其聚合签名(cagg, σagg) 上传至融合树中的下一跳节点.
步骤4 数据恢复与签名验证
首先是数据的恢复,根据笔者算法中的融合过程,不同节点的数据在编码后被连接组合成了一个新的数据,最终基站获取的即该组合后的数据,即
| $ {c_{{\rm{agg}}}} = \sum\limits_{i = 1}^t {{c_i}} = \sum\limits_{i = 1}^t {{m_i}\left\| {{0^{l(i - 1)}}} \right.} $ |
此时通过对该数据的分解mi′=cagg[(i-1)l, il-1],其中l为能表示网络中所有传感器节点采集原始数据mi的最小bit长度,i为节点的下标.
此时,基站节点获取到了每一个节点数据的编码信息,根据信源编码的译码过程,进行计算为
| $ {d_i}^\prime = D({m_i}^\prime ) = \mathop {{\rm{min}}}\limits_{{d_n} \in S} \left\| {{d_j} - {d_n}} \right\| $ |
其中:S为数据mi′所指向的陪集,dn为该陪集中的元素,dj为节点i对应的边信息,即在译码链中的ni.next=nj.
基站节点根据解码后的数据以及汇聚签名结果,对最终数据的完整性进行签名验证,验证过程为
| $ {e_n}({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \sigma } }_1},{g_2}) = \prod\limits_{i = 1}^{\eta - 1} {{e_n}({h_i},{P_{{n_i}}})} $ | (6) |
其中:hi=H(di),en为双线性映射[8].
如对于某节点数据式(6) 不成立,则表明此数据的完整性遭到了破坏,将该数据丢弃,反之可接收.
4 仿真结果与分析在Tinyos仿真环境下对算法的性能参数进行仿真测量,并将其性能和已有典型研究成果如可恢复的隐藏数据聚合(RCDA,recoverable concealed data aggregation)[1]、保障隐私性和完整性的可恢复数据聚合(RPIDA,recoverable privacy-preserving integrity-assured data aggregation)[5]进行了比较分析,表 1中给出了仿真环境参数的具体设置.
|
|
表 1 仿真参数表 |
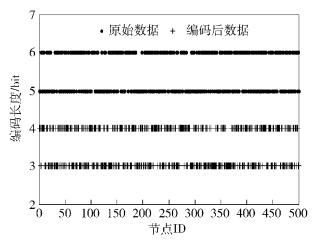
首先对于2种相关性模型下的信源编码的编码效率进行了测试,信源编码的压缩效率主要取决于数据间的相关性,相关性越高其编码效率也就越高,也就意味着能达到的数据压缩比越大.第1种模型中,假设样本空间为均值为30、标准差为2的温度数据500组,样本间的最小距离Δ=1,且满足简单的线性相关性模型m=ad+N,其中d为待编码的数据,m为其在编码链表的后集结点数据(即边信息).结果如图 2所示,在该模型下原始数据的编码一般需要5~6位,而经过分布式相关信源编码后的数据位数减少至3~4位,编码压缩比例约为P=35%.
|
图 2 原始数据与编码后数据长度分布 |
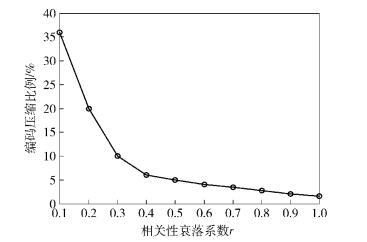
第2种相关模型中假设节点i采集的数据di满足均值为0、方差为σ2的联合高斯随机过程.对于任意2个节点采集的数据di和dj,其协方差为cov (di, dj)=σ2e-rdij,其中dij为节点i和j之间的距离,r为空间相关性衰减系数且r∈[0, 1],r越小相关性就越大,反之相关性就越小.结果如图 3所示,r对于信源编码的编码效率有着直接的影响,数据空间相关系数最大时,编码压缩比例可达到约36%,随着相关性的进一步降低,数据压缩比例逐步下降.
|
图 3 编码压缩性能随相关系数的变化 |
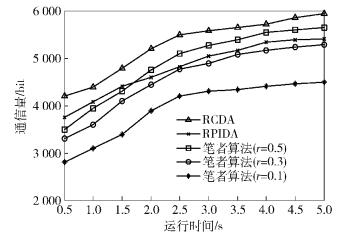
第2组实验主要针对融合过程中的数据通信量进行了比较.试验中采用了文献[1]示出的测量结果,数据长度322 bit,签名长度161 bit.根据这一数据,RCDA算法中,终端节点传输的数据总长度为483 bit,RPIDA则为368 bit.实验中将r分别取值为0.1,0.3和0.5,如笔者算法在空间相关性衰减系数r=0.2的情况下压缩比例可达到20%左右,即数据部分可压缩到257 bit,结果如图 4所示.相对于RCDA和RPIDA,笔者方案在进行数据隐藏的同时很好地实现了数据的压缩,使得整体通信量显著下降.
|
图 4 数据通信量对比 |
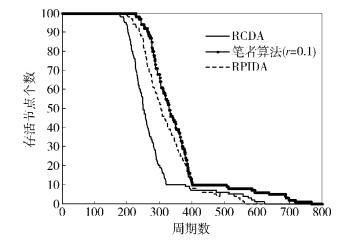
为了检验笔者方案在能量开销方面的性能,第3组实验中统计了不同方案下存活节点的分布情况,结果如图 5所示.实验中,设置节点的初始能量为0.5 J,参照已有的测试结果,节点在发送数据和接收数据的过程中消耗的能量分别为0.6 μJ/bit和0.67 μJ/bit.实验结果表明,笔者方案在数据通信开销方面相比RCDA和RPIDA有一定程度的降低,使得网络中节点的生命周期延长了约30%.
|
图 5 存活节点分布情况 |
分析了现有的无线传感器网络可恢复数据融合方案,在此基础上将信源编码技术用于数据的隐藏和压缩,实现了一种轻量级的数据融合隐私保护方案.理论分析和仿真结果表明,笔者方案既能保证数据的机密性、完整性、新鲜性,同时在通信量、通信开销等方面的性能上优于现有的算法.
| [1] | Chen Chienming, Lin Yuehsun, Lin Yaching, et al. RCDA:recoverable concealed data aggregation for data integrity in wireless sensor networks[J]. IEEE Trans on Parallel and Distributed Systems, 2012, 23(4): 727–734. doi: 10.1109/TPDS.2011.219 |
| [2] | Jose J, Kumar M, Joyce J. Energy efficient recoverable concealed data aggregation in wireless sensor networks[C]//Proc of the IEEE International Conference on Emerging Trends in Computing, Communication and Nanotechnology. Beijing:IEEE, 2013:322-329. |
| [3] | Ren Shuqin, Aung K M, Park J S. A privacy enhanced data aggregation model[C]//Proc of the 10th IEEE International Conference on Computer and Information Technology. Bradford:IEEE, 2010:985-990. |
| [4] | Wu Dapeng, Tang Jichao, Sun Qingwen. Recoverable concealed data aggregation for privacy preserving in wireless sensor networks[C]//Proc of 5th International Conference on Biomedical Engineering and Informatics. Chongqing:[s. n.], 2012:1499-1503. |
| [5] | Yang Lijun, Ding Chao, Wu Meng. RPIDA:recoverable privacy-preserving integrity-assured data aggregation scheme for wireless sensor networks[J]. KSII Trans on Internet and Information Systems, 2015, 12(9): 5189–5208. |
| [6] |
秦智超, 周正, 赵小川. 一种分簇无线传感器网络中的分布式信源编码算法[J]. 电子与信息学报, 2013, 35(2): 328–334.
Qin Zhichao, Zhou Zheng, Zhao Xiaochuan. A distributed source coding algorithm for clustering wireless sensor networks[J]. Journal of Electronics and Information Technology, 2013, 35(2): 328–334. |
| [7] | Shen Limin, Ma Jianfeng, Liu Ximeng. A secure and efficient ID-based aggregate signature scheme for wireless sensor networks[EB/OL]. (2016-04-21). http://ieeexplore.ieee.org/document/7457608. |
| [8] | Boneh D, Gentry C, Lynn B. Aggregate and verifiably encrypted signatures from bilinear maps[C]//Proc of International Conference on Theory and Applications of Cryptographic Techniques. Warsaw:[s.n.], 2003:416-432. |


