可见光通信(VLC, visible light communication) 使用发光二极管作为光源，在有效照明的同时进行高速通信.由于发光二极管带宽有限，在VLC系统中使用正交频分复用(OFDM, orthogonal frequency division multiplexing) 技术，可以提高VLC系统中的频谱利用率.单极性OFDM (U-OFDM, unipolar OFDM) 是近年来新提出的OFDM系统中的一种，比直流偏置光OFDM (DCO-OFDM, DC-biased optical OFDM) 具有更高的功率效率，比非对称限幅光OFDM (ACO-OFDM, asymmetrically clipped optical OFDM) 具有更高的频谱利用率.所以，U-OFDM更适合用于VLC系统.由于OFDM本身多载波正交性的特点，精确的同步技术对整个OFDM系统性能有着决定性的影响.现在已经有很多关于光OFDM同步的经典算法^[1-3]，但是还没有针对U-OFDM系统结构的同步算法.

笔者提出了一种新的针对于U-OFDM系统的负镜像对称(NMI, negative mirror image) 同步算法，该算法基于U-OFDM符号特性设计了相应的同步训练序列.仿真结果和分析表明，与Schmidl算法和Park算法相比，NMI算法具有明显的优越性.

1 光OFDM

对于传统的强度调制/直接检测的光通信系统而言，通常的解决方法就是在电-光信号转换的时候为OFDM信号加上直流偏置，这样使得双极性信号变为单极性信号，从而可以在光上传输.这种方法叫作DCO-OFDM.由于增加了直流偏置，导致传输信号的峰均功率比增大，降低调制深度，系统的功率效率变差.另一种方法是ACO-OFDM，只选择奇数子载波传输调制数据，同时把偶载波调制数据置零，快速傅里叶反变换后保留正实数信号.ACO-OFDM的功率效率比DCO-OFDM要高很多，但是由于只有奇载波传输数据，所以频谱效率只有DCO-OFDM的一半.然而，一种新的调制机制--U-OFDM备受关注，它使用一种新的排列方式使信号能够达到VLC系统的要求，且U-OFDM系统的峰均功率比优于DCO-OFDM，在频谱效率方面优于ACO-OFDM.

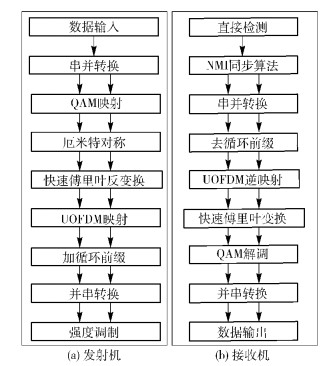
2 U-OFDM系统

VLC系统中U-OFDM收发端的数字信号处理框图如图 1所示.

在发射端，输入的串行数据首先被转换成并行数据，而后被映射成与子载波相对应的信息符号来组成一个OFDM符号.数据经过厄米特对称(见式(1)) 使基带信号变为实值信号，也就是说子载波k的信息符号和子载波N-k的信息符号相互为复共轭.

$ {C_{N-k}}=C_k^* $

(1)

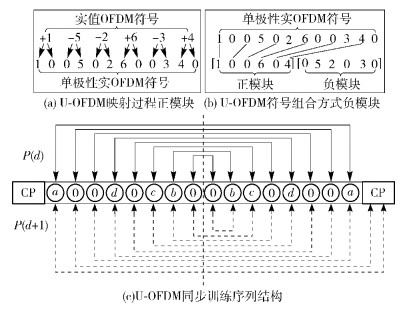
实值信号通过U-OFDM映射把双极性信号变为单极性信号.U-OFDM映射规则：如果OFDM符号中子载波上的数据a是正实数，那么它将会被映射为(a, 0)；如果OFDM符号中子载波上的数据是负实数b，那么它就会被映射为(0, |b|).U-OFDM的映射方式如图 2(a)、(b)所示.

信号经过图 2(a)所示的第1步映射后，每个OFDM符号都会映射出2个OFDM符号.原OFDM符号称为正模块，根据原OFDM符号映射出的新OFDM符号称为负模块，如图 2(b)所示.经过整合的正、负模块组合在一起得到U-OFDM信号.可以看出U-OFDM信号是单极性实信号，可以用在强度调制的VLC系统中.接收端U-OFDM信号通过光电探测器来接收，且可通过所提出的NMI同步算法精准确定信号的初始位置.经过同步后，接收到的U-OFDM信号去除循环前缀，U-OFDM信号逆映射，其中逆映射的过程是正模块中的OFDM符号减去负模块中相对应的OFDM符号，得到原始的双极性OFDM信号.其余的解调和处理方法与传统的OFDM系统一样.

3 NMI同步算法

Schmidl算法和Park算法是用在射频OFDM系统中的传统同步算法.2种经典的同步算法同样可应用于VLC系统中.但是，要对传统的训练序列做相应的改变，将实值非负序列$\left[{{A_{\frac{N}{2}}}\;\;\;{A_{\frac{N}{2}}}} \right]$和$\left[{{C_{\frac{N}{4}}}\;\;\;{D_{\frac{N}{4}}}\;\;\;{C_{\frac{N}{4}}}\;\;\;{D_{\frac{N}{4}}}} \right]$(D序列是C序列的镜像对称) 分别作为Schmidl算法和Park算法的训练序列，替代原有的复值双极性序列$\left[{{A_{\frac{N}{2}}}\;\;\;{A_{\frac{{\mathop N\limits^* }}{2}}}} \right]$和$\;\left[{{C_{\frac{N}{4}}}\;\;\;{D_{\frac{{\mathop N\limits^* }}{4}}}\;\;\;{C_{\frac{N}{4}}}\;\;\;{D_{\frac{{\mathop N\limits^* }}{4}}}} \right]$(“*”表示取共轭)^[4].Schmidl算法定时测量函数在正确的定时点附近的峰值平台依然存在；Park算法在信噪比(SNR, signal noise to ratio) 较高时能产生尖锐的脉冲形状的定时测量曲线，但是由于其训练序列结构，N/4处存在旁峰，低SNR时会出现旁峰替代主峰情况，导致VLC系统中的定时同步性能下降.

根据U-OFDM符号的特性，设计了一种新的NMI同步算法的训练序列，该算法的同步精度优于传统的同步算法.在VLC系统的发射端，训练序列和数据由相同的硬件或仿真产生.在信号进行U-OFDM映射之前，时域的训练序列结构为

$ s=\left[{{A_{\frac{N}{2}}}\;\;\;{B_{\frac{N}{2}}}} \right]\; $

(2)

其中：${{A_{\frac{N}{2}}}}$为实值的序列，长度为$\frac{N}{2}$(N为OFDM子载波个数)；${{B_{\frac{N}{2}}}}$为${{A_{\frac{N}{2}}}}$的负镜像对称.为简单起见，假设N=8，A包含了4个实数，如a, -b, -c, d，相对应的B应该是-d, c, b,-a.其中a, b, c, d都是正值，相对应的-a, -b, -c, -d都是负值，则

$ s=\left[{a, -b, -c, d, -d, c, b, - a} \right] $

(3)

首先，s中的每个样本按照U-OFDM映射法则重新定义为

$ \begin{array}{l} {s^1}=[\left({\boldsymbol{a}, 0} \right)\left({\boldsymbol{0}, b} \right)\left({\boldsymbol{0}, c} \right)\left({\boldsymbol{d}, 0} \right)\vdots \\ \;\;\;\;\;\;\;\left({\boldsymbol{0}, d} \right)\left({\boldsymbol{c}, 0} \right)\left({\boldsymbol{b}, 0} \right)\left({\boldsymbol{0}, a} \right)] \end{array} $

(4)

其次，s¹中每对数据的前面的部分(标记为粗体) 按照原来的顺序放在训练序列的前半部分的正模块中，其余的按照原来的顺序放在后半个部分的负模块中.最后产生的U-OFDM训练序列信号结构如图 2(c)所示.

可以看出，该训练序列在$\frac{N}{2}$处有很明显的中心对称，而且没有其他明显的对称.信号加上循环前缀后，训练序列的对称性也不会受到影响，因为循环前缀复制的是训练序列后面部分的样值.根据对称结构，时间同步执行基于上面提出的新训练序列的自相关性质.

相关的定时度量函数为^[5]

$ M\left(d \right)=\frac{{{{\left| {P\left(d \right)} \right|}^2}}}{{{{\left({R\left(D \right)} \right)}^2}}} $

(5)

其中

$ P\left(d \right)=\sum\limits_{m=0}^{\frac{N}{2}-1} {r\left({d-m} \right)r} \left({d+m+1} \right), {\rm{ }}0 \le m \le \frac{N}{2}-1 $

(6)

$ R\left(d \right)=\sum\limits_{m=0}^{\frac{N}{2}-1} {{{\left| {r\left({d+m+1} \right)} \right|}^2}} $

(7)

R(d) 作为能量归一化是总能量序列和的后一半.m为信号的滑动窗口数.

当M(d) 达到最大值时，这时的d就是正确的同步时间点.根据NMI训练序列结构，当d位于训练序列的中间点时，P(d) 和M(d) 同时得到最大值.

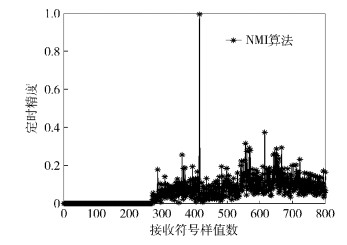
4 仿真及结果分析

仿真使用Matlab软件进行，根据NMI同步训练序列对称结构，可分析出，在其同步训练序列的中间点$\frac{N}{2}$处，有且仅有一个明显峰值，对应正确的时间点，且无其他旁峰.图 3中的仿真结果与理论分析完全一致，验证了前述的理论推导结果是正确的.

在Matlab软件平台下搭建VLC系统，可见光系统的信道有2种形式：直射信道和漫射信道^[6-7].其中漫射信道中定义6次反射.对新提出的适用于可见光U-OFDM系统的NMI同步算法在这2种信道中均做了仿真验证.在直射信道中，接收到的光是直射光；在漫射信道中，接收到的光仅含反射光.室内光无线系统漫射信道的脉冲响应可用指数式的衰减来建模，它和房间的大小以及室内表面的平均反射率有关：

$ {h_i}=\frac{{{{\rm{e}}^{-i{t_s}/\tau }}}}{{\sum\limits_{i=0}^{L-1} {{{\rm{e}}^{-i{t_s}/\tau }}} }} $

(8)

其中：L为抽头数，t_s为一个OFDM符号间隔时间，τ为延迟时间.

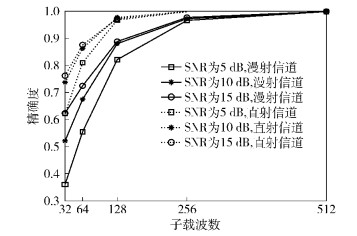
U-OFDM系统中子载波数对NMI算法的影响如图 4所示.在直射信道和漫射信道的仿真实验中，采用蒙特卡洛算法进行仿真.由于VLC通信中多径效应影响定时同步的准确性，而用来抵制多径效应的循环前缀数量随着子载波数的减少而减少，所以在较多子载波数时，能获得良好的定时同步精确度.

所以，后面的仿真实验中设定OFDM信号的子载波数为256，循环前缀长度G为16，即在d=(N+G)+G+N/2=416处有且只有一个明显峰值.训练序列和数据信号采用16QAM调制格式.为了公平比较，Schmidl算法和Park算法也都采用相同参数在U-OFDM系统中进行蒙特卡洛算法仿真.用正确时间点发生的概率表示定时同步算法的准确性.在直射信道和漫射信道中采用3种同步算法在不同的SNR情况下得到的精确度的对比如图 5所示.可以看出，在直射信道，Schmidl算法由于平台效应精确度很低；SNR大于10 dB时，Park算法的同步精确度与NMI算法的同步精确度相当；NMI算法精确度在SNR为2 dB时就可以达到99%以上，当SNR大于10 dB时精确度可达到100%.在漫射信道，当SNR大于10 dB时，Park算法精确度可达到85%，但是在低SNR时，NMI算法表现仍然优秀，当SNR大于5 dB时，NMI算法的定时同步精确度就可达到96%以上.

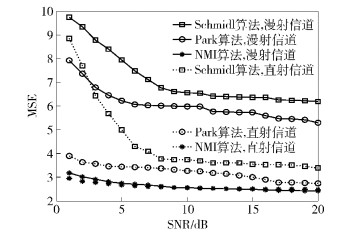
图 6是VLC仿真实验中U-OFDM信号在直射信道和漫射信道下在接收端分别进行3种同步算法后，计算得到的定时同步估计均方误差(MSE, mean squared error) 曲线.由于Schmidl算法中平台效应的存在，故MSE很高；Park算法由于旁峰的影响，在低SNR时，MSE也很高；NMI算法在低SNR情况下定时同步精确度依然很好.所以NMI算法的定时估计MSE最小，说明NMI算法的稳定性最好.

5 结束语

提出了一种新的定时同步算法--NMI算法，利用其新的训练序列结构，可获得精准的定时同步效果.在基于U-OFDM的VLC系统中，NMI算法的准确性通过具体的实例得到证实.与Schmidl算法和Park算法比较来看，NMI算法在直射信道和漫射信道都有着更好的定时同步性能.仿真结果显示，NMI算法即使在较低的SNR情况下也能找到正确的同步时间点，有着很高的准确度且几乎不受其他错误时间点的影响.