大规模多入多出(massive MIMO, massive multiple-input multiple-output) 网络是指在基站侧配置成百上千根天线，从而实现更大的复用、分集和阵列增益.传统的最小均方误差(MMSE，minimum mean-squared-error)^[1]检测广泛应用于无线通信中，然而它会引入矩阵求逆运算，具有3次幂的计算复杂度.对于massive MIMO网络来说，该检测技术复杂度很高.因此，低复杂度的检测技术成为业内学者研究的热点.Hoydis等^[2]通过对角矩阵求逆运算简化了MMSE检测算法，但降低了系统性能.Kim等^[3]提出了一种新型的接收机结构，它使得每个用户使用一条射频链路就能近似达到传统接收机中每根天线使用一条射频链路时的性能.

笔者将最陡下降(SD，steepest descent) 和最小均方(LMS，least mean-square) 算法应用于MMSE检测中，提出了massive MIMO网络中一种新型的MMSE接收机结构，避免了大规模矩阵求逆运算.

1 系统模型

考虑一个上行大规模多用户MIMO系统，配置有N_r根天线的基站在同一时-频资源块上同时服务N_t个单天线用户.在l时刻，用户k的发送符号为x_k(l)，E{x_k(l)}=0，且E{|x_k(l)|²}=1，|·|表示求模运算.那么，基站接收到的N_r维信号矢量可以表示为

$ \boldsymbol{y}\left(l \right)=\boldsymbol{H}{\boldsymbol{D}^{\frac{1}{2}}}x\left(l \right)+\boldsymbol{n}\left(l \right) $

(1)

其中：x(l)=(x₁(l), x₂(l), …, x_Nt(l))^T为发送符号矢量；大尺度衰落矩阵是对角矩阵D=diag (β₁, β₂, …, β_Nt)，β_k=z_k/r_k^θ为慢衰系数，z_k服从对数正态分布，θ为衰落因子，r_k为第k个用户到基站的距离；H_Nr×Nt为快衰信道矩阵，其中元素h_ij表示从第j个用户到基站上第i根天线间的快衰系数(考虑在强散射环境下的非相关平坦瑞利衰落信道，此时H_Nr×Nt中的元素是独立同分布的复高斯随机变量，均值为0，方差为1)；n(l) 为归一化的零均值加性高斯白噪声且E(n(l)n(l)⁺)=1/ρI_Nr，ρ为每个用户的发射信噪比(SNR，signal-to-noise ratio).(·)^T和(·)⁺分别表示矩阵的转置和共轭转置.

2 MMSE接收机结构 2.1 传统MMSE接收机

对于用户k，一般线性接收机的检测结果可以表示为${{\hat x}_k}$(l)=w_k⁺y(l)，其中w_k为线性变换矩阵.那么，实际发送信号与检测值之间误差为

$ \varepsilon(l)={x_k}(l)-{{\hat x}_k}\left(l \right) $

(2)

均方误差(MSE，mean squared error) 为

$ J\left(l \right)={E_{{n_k}\left(l \right), {x_k}(l)}}\{ {\varepsilon ^2}\left(l \right)\} $

(3)

则MMSE接收机为

$ {\boldsymbol{w}_k}=\mathop {{\rm{argmin}}}\limits_{{\boldsymbol{w}_k}} J\left(l \right) $

(4)

假设不同用户的发送符号和噪声之间两两相互独立，又因为实值目标函数J(l) 的曲率方向由共轭梯度矢量给出^[4]，可以得到

$ {\nabla _{\boldsymbol{w}_k^*}}\left[{J\left(l \right)} \right]=\boldsymbol{R}{\boldsymbol{w}_k} -{\boldsymbol{h}_k}d_{kk}^{\frac{1}{2}}=0 $

(5)

其中d_kk=β_k，当基站侧能够获取完美的信道状态信息(CSI，channel state information) 时，式(5) 的维纳解为

$ {\boldsymbol{w}_k}={\boldsymbol{R}^{-1}}{\boldsymbol{h}_k}d_{kk}^{\frac{1}{2}} $

(6)

其中：R=E_{n(l), x(l)}{y(l)y(l)⁺}=$\boldsymbol{\widetilde R}$+$\frac{1}{\rho }$I_Nr，$\boldsymbol{\widetilde R}$=HDH⁺；h_k为H的第k列，也就是说，h_k表示用户k到基站的信道矢量.

另一方面，用户k的接收信干噪比(SINR, signal-to-interference-plus-noise ratio) 可以表示为

$ {\gamma _k}=\frac{{\rho |\boldsymbol{w}_k^+{\boldsymbol{h}_k}{|^2}}}{{\sum\limits_{i=1, i \ne k}^{{N_t}} {\rho |\boldsymbol{w}_k^+{\boldsymbol{h}_i}{|^2}+{{\left\| {\boldsymbol{w}_k^+} \right\|}^2}} }} $

2.2 SD算法

式(5) 的解法大致可以分为两类：直接法和迭代法.直接法有QR分解、Gauss-Jordan或者Householder变换等，可以求得准确解.然而，当矩阵维数变得很大时，直接法会导致数值不稳定.迭代法就会被优先考虑，这里考虑相对简单的SD算法，矢量$\boldsymbol{\hat w}_k^{l+1}$按下述递推公式更新：

$ \boldsymbol{\hat w}_k^{l+1}=\boldsymbol{\hat w}_k^l-{k_s}{\nabla ^l} $

(7)

其中：$\boldsymbol{\hat w}_k^l \buildrel \Delta \over=$更新之前的权值矢量；$\boldsymbol{\hat w}_k^{l+1} \buildrel \Delta \over=$更新之后的权值矢量；k_s$ \buildrel \Delta \over=$控制因子，k_s>0；Δ^l$ \buildrel \Delta \over=$J(l) 关于$\boldsymbol{\hat w}_k^l$的共轭梯度，则

$ {\nabla ^l}=\boldsymbol{R}\boldsymbol{\hat w}_k^l-{\boldsymbol{h}_k}d_{kk}^{\frac{1}{2}} $

(8)

假设整个迭代过程中快衰矩阵H_Nr×Nt保持不变，式(8) 是关于发送符号x(l) 和噪声n(l) 的数学期望值，通过有限的迭代次数后就可以尽可能准确地检测出每个发送符号.

2.3 LMS算法

将式(8) 中的数学期望项用瞬时值代替，得到的梯度估计值称为瞬时梯度，用${{\hat \nabla }^l}$表示.假设每接收到一个新的符号，接收端都执行迭代算法.为了达到可观的检测性能，就需要足够长度的训练序列.

在时刻l，用权值矢量$\boldsymbol{\hat w}_k^l$去检测符号x_k(l)，依照最大似然原则判决之后得到估计后的符号值.此时，瞬时符号误差的二次方值用ε_ins²(l) 表示，则

$ {{\hat \nabla }^l}=\nabla \boldsymbol{\hat w}_k^{l*}\left[{\varepsilon _{{\rm{ins}}}^2\left(l \right)} \right] -\boldsymbol{y}\left(l \right)\left({x_k^+\left(l \right)-{\boldsymbol{y}^+}\left(l \right)\boldsymbol{\hat w}_k^l} \right) $

(9)

对于一个给定的$\boldsymbol{\hat w}_k^l$，则

$ E\left\{ {{{\hat \nabla }^l}} \right\}=\boldsymbol{R\hat w}_k^l-{\boldsymbol{h}_k}d_{kk}^{\frac{1}{2}} $

(10)

比较式(8) 和式(10)，容易发现瞬时梯度矢量是真实梯度矢量的无偏估计.用${{{\hat \nabla }^l}}$代替▽^l，式(7) 变为

$ \boldsymbol{\hat w}_k^{l+1}=\boldsymbol{\hat w}_k^l-{k_s}\boldsymbol{y}\left(l \right)\boldsymbol{\varepsilon} _{{\rm{ins}}}^+\left(l \right) $

(11)

式(11) 可以直接应用于数字通信系统中.

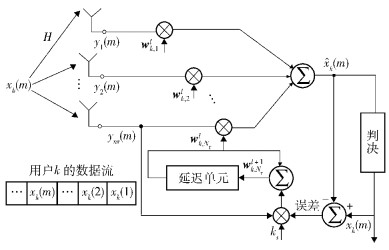
图 1是基于上述方程设计的MMSE接收机结构框图.其中，y_i(m) 为第i根天线上接收到的信号分量，w_{k, i}^l为权值矢量$\boldsymbol{\hat w}_k^l$的第i个分量，w^l+1_{k, Nr}为$\boldsymbol{\hat w}_k^{l+1}$的第N_r个分量，i=1, 2, …, N_r.由图 1可以看出，每个接收天线单元都可以单独执行迭代算法，且在每次迭代中需要1次加法、1次减法和2次乘法运算.所以，该接收机所需要总的计算复杂度为O(MN_r)，其中M为迭代次数.

同样地，在模拟通信系统中，式(11) 可以写成

$ \frac{{\rm{d}}}{{{\rm{d}}t}}{\boldsymbol{w}_k}\left(t \right)={k_s}\boldsymbol{y}\left(t \right)\varepsilon _{{\rm{ins}}}^+\left(t \right) $

(12)

3 收敛性分析

对于SD算法，初始权值矢量记为$\boldsymbol{\hat w}_k^0$，经过l+1次迭代之后，式(7) 变为

$ \boldsymbol{\hat w}_k^{l+1}={[\boldsymbol{I}-{k_s}\boldsymbol{R}]^{l+1}}\boldsymbol{\hat w}_k^0+{k_s}{\sum\limits_{i=0}^l {\left[{\boldsymbol{I}-{k_s}\boldsymbol{R}} \right]} ^i}{\boldsymbol{h}_k}d_{kk}^{\frac{1}{2}} $

(13)

注意到R是Hermitian矩阵，存在相似变换矩阵Q，使得R=Q^-1EQ.其中E=diag (e₁, e₂, …, e_Nr) 为由R的特征值组成的对角矩阵.易知R是正定的，则所有的特征值是正的.进一步化简可得

$ \boldsymbol{\hat w}_k^{l+1}={[\boldsymbol{I}-{k_s}\boldsymbol{R}]^{l+1}}\boldsymbol{\hat w}_k^0+{k_s}{\sum\limits_{i=0}^l {\left[{\boldsymbol{I}-{k_s}\boldsymbol{R}} \right]} ^i}{\boldsymbol{h}_k}d_{kk}^{\frac{1}{2}} $

(14)

考虑对角矩阵I-k_sE，只要每个对角元素的绝对值小于1，那么

$ \mathop {{\rm{lim}}}\limits_{l \to \infty } {[\boldsymbol{I}-{k_s}\boldsymbol{E}]^{l+1}} \to 0 $

(15)

依据级数求和法则，有

$ \mathop {{\rm{lim}}}\limits_{l \to \infty } {\sum\limits_{i=0}^l {[\mathit{\boldsymbol{I}}-{k_s}\mathit{\boldsymbol{E}}]} ^i}=\frac{1}{{{k_s}}}{\mathit{\boldsymbol{E}}^{ -1}} $

(16)

从而，式(14) 变为

$ \mathop {{\rm{lim}}}\limits_{l \to \infty } \mathit{\boldsymbol{\hat w}}_k^{l+1}={\mathit{\boldsymbol{Q}}^{-1}}\mathit{\boldsymbol{EQ}}{\mathit{\boldsymbol{h}}_k}d_{kk}^{\frac{1}{2}}={\boldsymbol{R}^{-1}}{\mathit{\boldsymbol{h}}_k}d_{kk}^{\frac{1}{2}} $

(17)

下面讨论LMS算法.假定y(l) 和y(l+1) 不相关，则LMS算法中权值矢量的期望值可以写成

$ E\left\{ {\boldsymbol{\hat w}_k^{l+1}} \right\}=E\left\{ {\boldsymbol{\hat w}_k^l} \right\}-{k_s}{\nabla ^l} $

(18)

从而可以发现，LMS算法中权值矢量的期望值也是收敛的.

最后，讨论SD算法和LMS算法的收敛条件.式(13) 中$\boldsymbol{\hat w}_k^{l+1}$又可以写成

$ \begin{array}{l} \mathit{\boldsymbol{\hat w}}_k^{l+1}={\mathit{\boldsymbol{Q}}^{- 1}}{[\mathit{\boldsymbol{I}}-{k_s}\mathit{\boldsymbol{E}}]^{l+1}}\mathit{\boldsymbol{Q}}\left({\mathit{\boldsymbol{\hat w}}_k^0 -{\mathit{\boldsymbol{R}}^{ -1}}{\mathit{\boldsymbol{h}}_k}d_{kk}^{\frac{1}{2}}} \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{R}}^{ -1}}{\mathit{\boldsymbol{h}}_k}d_{kk}^{\frac{1}{2}} \end{array} $

(19)

由式(19) 可看出，权值矢量收敛到维纳解需要的条件为|1-k_se_max| < 1.其中e_max为R的最大特征值.

用H_i表示h_id_iih_i⁺(i=1, 2, …, N_t)，在massive MIMO网络中，当N_r→∞时，有^[5]

$ {\boldsymbol{h}_i}{d_{ii}}\boldsymbol{h}_i^+={\beta _i}\boldsymbol{I} $

(20)

应用Weyl定理^[5]，可以推出

$ {e_{{\rm{max}}}} \ge \frac{1}{\rho }+{\rm{max}}\{ {\lambda _1}, {\lambda _2}, \ldots, {\lambda _{{N_{\rm{t}}}}}\} $

(21)

其中λ_i为H_i的最大特征值，也就是λ_i=β_i，那么

$ 0 <{k_s} <\frac{1}{{\frac{2}{\rho }+\max \{ {\lambda _1}, {\lambda _2}, \ldots, {\lambda _{{N_{\rm{t}}}}}\} }} $

(22)

进一步地，考虑到massive MIMO网络中不同信道之间是近似正交的特点^[5]，可以得到R的近似表达式为$\boldsymbol{R}=\left({{\rm{tr}}\left\{ \boldsymbol{D} \right\}+\frac{1}{\rho }} \right){\boldsymbol{I}_{{N_{\rm{r}}}}}$.

由上述分析可知，收敛速度本质上由CSI，尤其是慢衰系数决定，并受控制因子k_s取值影响.事实上，若要保证较快的收敛速度，k_s需满足条件：|1-k_se_max| < < 1.也就是说，当0 < k_s < $\frac{1}{{{e_{\max }}}}$时，收敛速度随着e_max增加而增加；当$\frac{1}{{{e_{\max }}}}$≤k_s < $\frac{2}{{{e_{\max }}}}$时，收敛速度变化趋势正好相反.

下面推导接收信号相关矩阵R对应最大特征值的概率密度分布.首先，$\boldsymbol{\widetilde R}$是中心分布的Wishart矩阵，矩阵D的特征值按降序排列可以表示为β_i1≥β_i2≥…≥β_iNt，其中i₁, i₂, …, i_Nt是1, 2, …, N_t的一种排列.不失一般性，当N_t < N_r时，$\boldsymbol{\widetilde R}$的特征值分布按降序排列为ψ₁≥ψ₂≥…≥ψ_Nt，则它们的联合概率密度可以表示为^[6]

$ {\frac{{{\rm{det}}(\{ {{\rm{e}}^{-{\varphi _j}/{\beta _{{i_n}}}}}\})}}{{{\rm{det}}\mathop \Sigma \limits^{{N_{\rm{r}}}} }}\prod\limits_{l=1}^{{N_{\rm{t}}}} {\frac{{\varphi _l^{{N_{\rm{r}}}-{N_{\rm{t}}}}}}{{({N_{\rm{r}}}-l)!}}} \prod\limits_{k <1}^{{N_{\rm{t}}}} {\frac{{{\varphi _k} - {\varphi _l}}}{{{\beta _{{i_k}}} - {\beta _{{i_l}}}}}{\beta _{{i_k}}}{\beta _{{i_l}}}} } $

则R的最大特征值Ω=max (ψ₁, …, ψ_Nt)+${\frac{1}{\rho }}$，它的累计分布函数为

$ \begin{array}{*{20}{c}} {{F_\mathit{\Omega }}\left(u \right)={\rm{Prob}}\left({\mathit{\Omega } \le u} \right)=}\\ {{\rm{Prob}}\left({{\psi _1} \le u-\frac{1}{\rho }, \ldots, {\psi _{{N_{\rm{t}}}}} \le u-\frac{1}{\rho }} \right)=}\\ {\int_0^{u-\frac{1}{\rho }} \cdots \int_0^{u - \frac{1}{\rho }} {{f_{{\psi _1}, \ldots, {\psi _{{N_{\rm{t}}}}}}}}({\varphi _1}, \ldots, {\varphi _{{N_{\rm{t}}}}})d{\varphi _1} \ldots d{\varphi _{{N_{\rm{t}}}}}} \end{array} $

4 仿真结果

在仿真中，8个用户均匀分布在距离基站10~100 m的范围内，路损指数设为2，基站天线个数为10.假定基站侧能够获取完美的CSI.

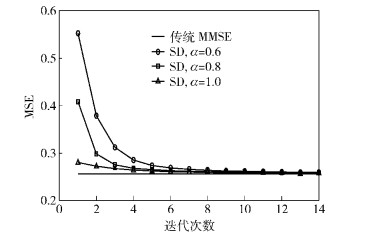
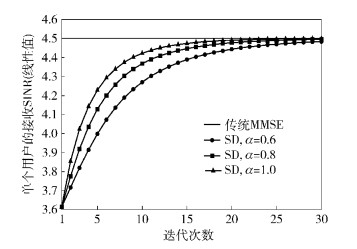
图 2所示为不同条件下线性值(MSE) 随迭代次数增加的进化曲线.其中，ρ=20 dB，k_s=αe_max^-1.可见，在该仿真条件下，经过10次迭代，SD算法的性能基本接近MMSE最优检测性能，且k_s的取值影响算法性能和收敛速度，验证了理论分析.实际应用中，可以选取合适的k_s以保证尽可能快的收敛速度.另一方面，在传统的MMSE接收机中，矩阵求逆的计算复杂度为O(N_r³).所以，当N_r值很大时，所提检测算法复杂度明显降低.类似地，以距离基站最近的用户为例，给出了该用户的接收SINR随迭代次数(从1开始) 增加的进化曲线(见图 3).

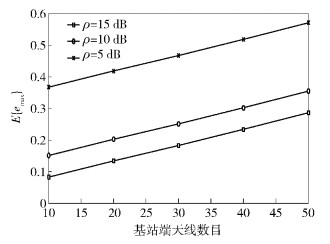
图 4给出了不同SNR条件下e_max的期望值大小随基站天线数目变化的关系.由图 4可见，基站天线数目越多，SNR越小，e_max的期望值越大.根据不同k_s取值可以确定接收端天线数目对迭代算法收敛速度的影响.

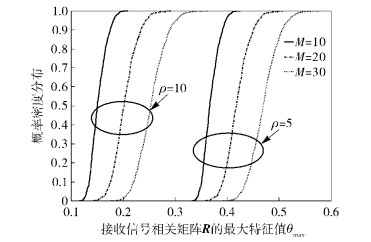
进一步地，图 5示出了接收信号相关矩阵R最大特征值的概率密度分布曲线，分别对应接收SNR为5 dB、10 dB，基站天线个数分别为10、20、30.

5 结束语

在Massive MIMO网络中应用传统的MMSE检测技术时，求解均衡矩阵需要大规模矩阵求逆运算，复杂度很高.笔者基于SD和LMS算法，设计出了一种新型的MMSE接收机结构，只需要利用少量的训练序列，经过较少的迭代运算之后就能近似得到最优的均衡矩阵，避免了矩阵求逆运算.换句话说，是以较小的空间复杂度换取了大量的时间复杂度.另外，由于每条射频链路上可以单独执行该算法，并行处理进一步降低了计算复杂度.同时，用数学证明了所提算法的收敛性，并分析了收敛条件以及影响收敛速度的因素.仿真结果表明，该接收机通过较少的迭代次数就可以达到较好的检测性能.