2. 哈尔滨工业大学 机器人技术与系统国家重点实验室, 哈尔滨 150001
针对通信系统中宽带功率放大器引起的非线性失真问题,提出了最小差错概率(MBER)算法,以优化非线性均衡器参数,并采用非线性均衡器与数字预失真器对功率放大器非线性失真进行联合补偿.预失真用于减少非线性失真对带外的干扰,非线性均衡器用于减少带内失真.仿真结果表明,基于MBER算法的非线性均衡器性能优于基于最小均方误差算法的均衡器;联合线性化简化了预失真器的结构,并可获得更优的误码率性能.
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China
A joint compensation by digital pre-distortion and nonlinear equalizers was proposed for nonlinear distortion of wide band power amplifiers in communications. The nonlinear equalizers are based on minimum bit error rate (MBER) algorithm. Out-band interference caused by nonlinear distortion is suppressed by digital pre-distorters, and in-band distortion is reduced by nonlinear equalizers. Simulations show that the performance of nonlinear equalizers based on MBER is superior to that based on minimum mean square error algorithm. Through joint compensation of pre-distortion and equalization, the digital distorters can be simplified and the performance of bit error rate can be improved.
在通信系统中,非线性失真会导致信号带内失真,增加误码率,在带外产生频谱扩展,对邻道造成干扰.正交振幅调制(QAM,quadrature-amplitude modulation)、正交频分复用(OFDM,orthogonal frequency division multiplexing) 等非恒包络信号因其高频谱利用率而被广泛应用于各种通信系统中[1].对非恒包络调制信号通信系统来说,功率放大器的非线性对通信信号失真的影响会更加严重.
最小差错概率(MBER,minimum bit error rate) 是通信系统设计追求的一个重要目标.为对非恒包络通信系统中的功率放大器非线性进行补偿,笔者先用一个低阶的预失真器进行初步线性化,以降低非线性失真对带外造成的干扰.对仍残余的非线性失真,在接收机中通过非线性均衡来消除.这样,既可简化预失真器的设计,又可以消除非线性失真的影响,降低系统的误码率.非线性均衡器采用MBER算法进行优化[2-4].仿真结果表明,与基于最小均方误差(MMSE,minimum mean square error) 算法的非线性均衡器相比较,基于MBER算法的非线性均衡器可获得更优的误码率性能.
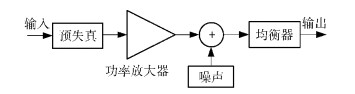
1 预失真系统整体实现框架如图 1所示.通信信号在发送机中经预失真后送入功率放大器.信道中的噪声为加性高斯白噪声.在接收机中,信号经均衡器处理后输出.
|
图 1 系统整体模型 |
系统的各部分分别采用不同的非线性模型建模.预失真器和均衡器采用Volterra序列(VS,Volterra series) 建模.功率放大器采用非线性维纳模型建模,且非线性预失真器采用间接学习算法训练;非线性均衡器采用最小差错概率准则算法训练.
功率放大器采用有记忆效应的非线性模型,这里采用维纳模型.维纳模型采用无记忆Volterra序列通过一个因果线性滤波器来实现,如图 2所示.

|
图 2 功率放大器模型 |
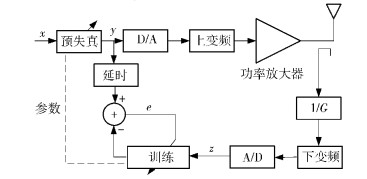
预失真框图如图 3所示.QAM基带信号先经预失真器进行预补偿,然后经D/A转换、上变频,再送到功放进行放大输出.从天线耦合下来的信号经下变频、A/D转换,然后作为预失真器参数的训练数据.在图 3中,延时的确定过程也是一个位信号同步的过程.
|
图 3 预失真模型 |
非线性预失真器可采用维纳模型、神经网络、Volterra序列等非线性模型实现[5].笔者采用Volterra序列来实现非线性预失真器.令VS (m, p, d(1)) 表示记忆深度为m,阶数为p,延迟为d(1)的Volterra序列.若采用VS (m, 2, d(1)) 模型,可表示为
| $ {{y}_{k}}=\sum\limits_{i=0}^{m-1}{h_{i}^{\left(1 \right)}}{{\boldsymbol{x}}_{k-i+{{d}^{\left(1 \right)}}}}+\sum\limits_{i=0}^{m-1}{\sum\limits_{j=i}^{m-1}{h_{i, j}^{\left(2 \right)}{{\boldsymbol{x}}_{k-i+{{d}^{\left(1 \right)}}}}}}\boldsymbol{x}_{k-i+{{d}^{\left(1 \right)}}}^{*} $ | (1) |
其中:xk为VS的输入向量,h(1)和h(2)为Volterra核,*为共轭.为便于表示,常将输入信号及其高阶项表示为矩阵形式.令
| $ \begin{align} &{{\boldsymbol{x}}_{k}}=[{{x}_{k+{{d}^{(1)}}}}, \ldots, {{x}_{k-(m-1-{{d}^{(1)}})}}, {{x}_{k+{{d}^{(1)}}}}x_{k+{{d}^{(1)}}}^{*}, \ldots, \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{k-(m-1-{{d}^{(1)}})}}x_{k-(m-1-{{d}^{(1)}})}^{*}{{]}^{\text{T}}}~ \\ \end{align} $ | (2) |
| $ \boldsymbol{w}={{\left[h_{0}^{(1)}, \ldots, h_{m-1}^{(1)}, h_{0, 0}^{\left(2 \right)}, \ldots, h_{m-1, m-1}^{(2)} \right]}^{\text{T}}} $ | (3) |
其中T为矩阵的转置.这样,可得
| $ {{y}_{k}}={{\boldsymbol{w}}^{\text{T}}}{{\boldsymbol{x}}_{k}}~ $ | (4) |
对QAM系统预失真器参数的训练采用间接学习算法[6-7],如图 3所示.图 3中1/G表示对功放进行G倍衰减.令z为功放的输出被耦合后,经衰减、下变频再A/D转换后得到的训练数据.若预失真器采用2阶VS序列,则
| $ {{\boldsymbol{z}}_{k}}={{[{{z}_{k+{{d}^{(1)}}}}, \ldots, \text{ }{{z}_{k-(m-1-{{d}^{(1)}})}}z_{k-\left(m-1-{{d}^{(1)}} \right)}^{*}]}^{\text{T}}} $ | (5) |
预失真器参数训练的目标函数为
| $ e\left(k, \boldsymbol{w} \right)=|y\left(k \right)-{{\left(z\left(k \right)\right)}^{\text{T}}}\boldsymbol{w}{{|}^{2}} $ | (6) |
其中w为归一化的参数矩阵.间接训练算法的解可表示为
| $ \boldsymbol{w}=\text{arg}~\underset{\boldsymbol{w}}{\mathop{\text{min}}}\, \text{ }e\left(\boldsymbol{w} \right) $ | (7) |
笔者采用随机梯度下降算法优化w,目标函数e(k, w) 的随机梯度为
| $ \nabla e\left(k, \boldsymbol{w} \right)=-{{(y\left(k \right)-{{\left(z\left(k \right)\right)}^{\text{T}}}\boldsymbol{w})}^{*}}\boldsymbol{z}\left(k \right) $ | (8) |
随机梯度下降算法的增益μ为
| $ {{\mu }_{l}}={{\mu }_{0}}{{l}^{-{{d}^{(2)}}}}({{d}^{(2)}}>0, l\ge 0) $ | (9) |
其中:l为下降迭代的步数,μ0为初始增益,d(2)为常数.预失真参数训练完成后,这些参数被复制到预失真器中进行基带信号的预失真,如图 3所示的虚线部分.
2 非线性均衡非线性均衡器可用神经网络、Volterra序列等实现,笔者采用VS来实现非线性均衡器,非线性均衡器的参数采用MBER算法进行训练.
2.1 非线性均衡器模型非线性均衡器模型采用VS,如图 4所示.

|
图 4 非线性均衡器模型 |
对基于VS (m, 3, d(1)) 的复值Volterra均衡器有
| $ \begin{align} &{{v}_{k}}=\sum\limits_{i=0}^{m-1}{h_{i}^{\left(1 \right)}}{{u}_{k-i+{{d}^{\left(1 \right)}}}}+\sum\limits_{i=0}^{m-1}{\sum\limits_{j=i}^{m-1}{h_{i}^{\left(2 \right)}{{u}_{k-i+{{d}^{\left(1 \right)}}}}}}u_{k-i+{{d}^{\left(1 \right)}}}^{*}+\\ &\ \ \ \ \ \ \ \ \ \ \ \sum\limits_{i=0}^{m-1}{\sum\limits_{l=i}^{m-1}{\sum\limits_{q=l}^{m-1}{h_{i}^{\left(3 \right)}{{u}_{k-i+{{d}^{\left(1 \right)}}}}{{u}_{k-l+{{d}^{\left(1 \right)}}}}}}}u_{k-q+{{d}^{\left(1 \right)}}}^{*} \\ \end{align} $ | (10) |
其中uk为复值的均衡器输入.对于VS (m, 3, d(1)) 模型,共有
| $ \left(\begin{matrix} m+p \\ m \\ \end{matrix} \right)=\frac{\left(m+p \right)\text{!}}{m\text{!}p\text{!}} $ | (11) |
为方便表示,将输入信号及其高阶项表示为矩阵形式,令
| $ {{\boldsymbol{u}}_{k}}={{[{{u}_{k+{{d}^{(1)}}}}, \ldots, {{u}_{k-(m-1-{{d}^{(1)}})}}{{u}_{k-(m-1-{{d}^{(1)}})}}u_{k-(m-1-{{d}^{(1)}})}^{*}]}^{\text{T}}}~ $ | (12) |
| $ \boldsymbol{w}={{\left[h_{0}^{(1)}, \ldots, h_{m-1, m-1, m-1}^{(3)} \right]}^{\text{T}}}~ $ | (13) |
则有
| $ {{v}_{k}}={{\boldsymbol{w}}^{\text{T}}}{{\boldsymbol{u}}_{k}} $ | (14) |
在数字通信系统中,线性均衡器参数的训练采用MMSE算法,与采用MBER算法是等价的.但对于非线性均衡器的参数,采用MBER算法训练相对于采用MMSE算法有优势.
令vR, k和vI, k分别为vk的实部和虚部,有
| $ {{v}_{k}}={{v}_{\text{R}, k}}+\text{j}{{v}_{\text{I}, k}} $ | (15) |
其中j为虚数单位.对输入信号uk用复值的Volterra均衡器处理后得到vk.假设QAM信号采用矩形星座点,有
| $ {{s}_{k}}={{a}_{k}}+\text{j}{{b}_{k}} $ | (16) |
其中:a, b∈{±1, ±3, …, ±(L+1)},L≥0为偶数.判决对实部、虚部分别进行,准则为
若l-1≤vR, k≤l+1,-L < l < L,则â k=l;
若vR, k≥L,则â k=L+1;
若vR, k≤-L,则â k=-(L+1).
其中â k为ak的估计值.对虚部的判决也采用类似准则得到bk的估计值
| $ {{{\hat{s}}}_{k}}={{{\hat{a}}}_{k}}+\text{j}{{{\hat{b}}}_{k}} $ | (17) |
在均衡器的参数训练中,考虑到QAM矩形星座点的对称性,构造函数为
| $ {{\xi }_{\text{R}, k}}=\text{sgn}~({{a}_{k}}){{v}_{\text{R}, k}}-(\text{sgn}~({{a}_{k}}){{a}_{k}}-1) $ | (18) |
其中sgn (·) 为符号函数.则根据上述判决准则,对于-L < ak < L,若ξR, k>2或ξR, k < 0时将误判;对于ak=±(L+1),若ξR, k < 0时将误判.令PR为数据实部误判的概率,令
| $ {{{\tilde{P}}}_{\text{R}, k}}=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }\rho }\text{exp}\left(~-\frac{{{(\alpha-{{\xi }_{\text{R}, k}})}^{2}}}{2{{\rho }^{2}}} \right) $ | (19) |
| $ \begin{align} &{{{\tilde{P}}}_{\text{R}, k}}=(1-\delta(\text{sgn}~({{a}_{k}}){{a}_{k}}-L-1))\times \\ &\left[\int_{-\infty }^{0}{\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}}\text{exp}\left(~-\frac{{{(\alpha-{{\xi }_{R, k}})}^{2}}}{2{{\rho }^{2}}} \right)\text{d}\alpha+\right.\\ &\left.\int_{2}^{+\infty }{\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}}\text{exp}\left(~-\frac{{{(\alpha-{{\xi }_{R, k}})}^{2}}}{2{{\rho }^{2}}} \right)\text{d}\alpha \right]+\\ &\ \ \ \ \ \ \ \delta(\text{sgn}~({{a}_{k}}){{a}_{k}}-L-1)\times \\ &\int_{-\infty }^{0}{\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}}\text{exp}\left(~-\frac{{{(\alpha -{{\xi }_{R, k}})}^{2}}}{2{{\rho }^{2}}} \right)\text{d}\alpha \\ \end{align} $ | (20) |
其中:ρ为Parzen窗宽度,α为积分变量,δ(·) 为构造的函数,性质有
| $ \delta \left(\alpha \right)=\left\{ \begin{align} &0, \ \ \ \ \alpha \ne 0 \\ &1, \ \ \ \ \alpha=0 \\ \end{align} \right. $ | (21) |
类似于对实部的讨论,设PI为数据虚部误判概率,令
| $ {{\xi }_{\text{I}, k}}=\text{sgn }\!\!~\!\!\text{ }({{b}_{k}}){{v}_{\text{I}, k}}-(\text{sgn}~({{b}_{k}}){{b}_{k}}-1) $ | (22) |
| $ \begin{align} &{{{\tilde{P}}}_{I, k}}=(1-\delta(\text{sgn}~({{b}_{k}}){{b}_{k}}-L-1))\times \\ &\left[\int_{-\infty }^{0}{\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}}\text{exp}\left(~-\frac{{{(\alpha-{{\xi }_{I, k}})}^{2}}}{2{{\rho }^{2}}} \right)\text{d}\alpha+\right.\\ &\left.\int_{2}^{+\infty }{\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}}\text{exp}\left(~-\frac{{{(\alpha-{{\xi }_{I, k}})}^{2}}}{2{{\rho }^{2}}} \right)\text{d}\alpha \right]+\\ &\ \ \ \ \ \ \ \delta(\text{sgn}~({{b}_{k}}){{b}_{k}}-L-1)\times \\ &\int_{-\infty }^{0}{\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}}\text{exp}\left(~-\frac{{{(\alpha -{{\xi }_{I, k}})}^{2}}}{2{{\rho }^{2}}} \right)\text{d}\alpha \\ \end{align} $ | (23) |
| $ {{{\tilde{P}}}_{\text{e}, k}}={{{\tilde{P}}}_{\text{R}, k}}+(1-{{{\tilde{P}}}_{\text{R}, k}}){{{\tilde{P}}}_{\text{I}, k}}\approx {{{\tilde{P}}}_{\text{R}, k}}+{{{\tilde{P}}}_{\text{I}, k}} $ | (24) |
式(24) 中采用近似,主要是考虑到
| $ {{P}_{\text{e}}}\left(\boldsymbol{w} \right)=\frac{1}{K}\sum\limits_{k=1}^{k}{{{{\tilde{P}}}_{\text{e}, k}}\left(\boldsymbol{w} \right)} $ | (25) |
其中K为训练样本总数.基于MBER准则均衡模型的解为
| $ \boldsymbol{w}=\text{arg}~\underset{\boldsymbol{w}}{\mathop{\text{min}}}\, \text{ }{{\text{P}}_{e}}\left(\boldsymbol{w} \right) $ | (26) |
| $ \begin{align} &\nabla {{{\tilde{P}}}_{e, k}}=-\left[(1-\delta(\text{sgn}~({{a}_{k}}){{a}_{k}}-L-1))\right.\times \\ &\ \ \ \ \ \ \ \ \ \ \ \left[\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}\text{exp}\left(~-\frac{{{({{\xi }_{R, k}})}^{2}}}{2{{\rho }^{2}}} \right)\right.-\\ &\ \ \ \ \ \ \ \ \ \ \left.\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}\text{exp}\left(~-\frac{{{(2-{{\xi }_{R, k}})}^{2}}}{2{{\rho }^{2}}} \right)\right]+\\ &\left.\delta(\text{sgn}~({{a}_{k}}){{a}_{k}}-L-1)\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}\text{exp}\left(~-\frac{{{({{\xi }_{R, k}})}^{2}}}{2{{\rho }^{2}}} \right)\right]\frac{\partial {{v}_{k}}}{\partial \boldsymbol{w}}- \\ &\left[\left(1-\delta(\text{sgn}~({{b}_{k}}){{b}_{k}}-L-1)\right)\right.\left[\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}\text{exp}\left(~-\frac{{{(2-{{\xi }_{I, k}})}^{2}}}{2{{\rho }^{2}}} \right)\right.-\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}\text{exp}\left(~-\frac{{{(2-{{\xi }_{I, k}})}^{2}}}{2{{\rho }^{2}}} \right)\right]+\\ &\delta(\text{sgn}~({{b}_{k}}){{b}_{k}}-L-1)\ \left.\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }\rho }}\text{exp}\left(~-\frac{{{(2-{{\xi }_{I, k}})}^{2}}}{2{{\rho }^{2}}} \right)\right]\frac{\partial {{v}_{k}}}{\partial \boldsymbol{w}} \\ \end{align} $ | (27) |
随机梯度算法每步迭代是用单个样点的Parzen窗来估计概率密度函数,数值不稳定且易进入局部极点.如果用k时刻和以前所有的数据来估计
| $ \nabla {{\tilde{P}}_{e, k}}\left(\boldsymbol{w} \right)=\sum\limits_{i=q}^{k}{\nabla {{{\tilde{P}}}_{e, i}}\left(\boldsymbol{w} \right)} $ | (28) |
| $ q=\text{max}~(0, k-{{m}^{(1)}}+1) $ | (29) |
其中m(1)为滑窗长度.
令增益μ为
| $ {{\mu }_{k}}={{\mu }_{0}}{{k}^{-{{d}^{(2)}}}}, \text{ }{{d}^{(2)}}\ge 0 $ | (30) |
其中d(2)等于0时,增益为常数.基于MBER准则的滑窗随机梯度训练算法如下.
步骤1 初始化:根据试验选定ρ、μ0、d(1)、d(2)和w0.
步骤2 对于第k步迭代,更新为
| $ {{\boldsymbol{w}}_{k+1}}={{\boldsymbol{w}}_{k}}-{{\mu }_{k}}(\nabla {{{\tilde{P}}}_{e, k}}({{\boldsymbol{w}}_{k}}))* $ | (31) |
步骤3 当分段测得Pe的改变量很小时,结束;否则,返回到步骤2.
3 仿真分析仿真基于Matlab平台的16QAM通信系统,预失真器及均衡器采用VS序列.信道中噪声为加性高斯白噪声.功率放大器采用维纳模型,滤波器的参数为[0.34-0.29j, 0.87+0.55j, 0.34-0.24j].无记忆的非线性模型为
| $ z=F\left({\hat{z}} \right)=\hat{z}+0.12{{\left({\hat{z}} \right)}^{2}}+0.07{{\left({\hat{z}} \right)}^{3}} $ | (32) |
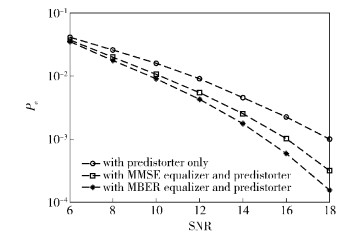
仿真中,预失真器采用VS (2, 2, 0),非线性均衡器采用VS (3, 3, 1).其中,预失真器采用间接学习算法训练VS参数,初始参数为μ0=0.01,d(2)=0.非线性均衡器采用MBER滑窗随机梯度算法训练参数,初始参数分别为m(1)=100,ρ=0.12,μ0=0.005,d(2)=0,w0=0.仿真分3种情况进行:第1种是仅使用预失真器进行线性化;第2种是采用预失真器与基于MMSE准则的均衡器联合线性化;第3种是采用预失真器与基于MBER准则均衡器联合线性化.仿真结果如图 5所示.从图 5中可以看出,基于MBER准则均衡器与预失真器联合线性化可获得更好的误码率性能.
|
图 5 误码率曲线 |
在非线性均衡器中,信号被非线性均衡,信道的噪声也同样被非线性处理,最小均方误差准则与最小差错概率准则在非线性均衡器参数训练中并不等价.系统的最终评价指标不是最小均方误差,而是最小差错概率,因此对于以MBER为目标的数字通信系统来说,采用MBER准则来训练非线性均衡器可获得更优性能,图 5的仿真结果也验证了这一点.MBER算法的主要困难在于差错概率的估计,这里是采用Parzen窗函数来估计概率密度函数,继而估计差错概率.因采用联合补偿,降低了对预失真器的要求,可显著降低预失真器的复杂度,进而降低了系统的整体复杂度.
4 结束语在QAM、OFDM等非恒包络通信系统中,功率放大器在追求高效率的同时也会带来严重的失真.针对非线性失真问题,笔者提出MBER优化算法训练非线性均衡器,采用预失真器与均衡器联合对功放进行线性化补偿.预失真器主要用于减少非线性失真引起的带外干扰;均衡器用于减少残余的失真所引起的带内失真,进一步降低误码率.仿真结果表明,采用联合补偿的方法,可简化预失真的设计,进一步降低误码率,且相对基于MMSE准则的均衡器,MBER均衡器可获得更优的误码率性能.虽然联合补偿在降低预失真器复杂度的同时可进一步优化误码率性能,但如何协调预失真与均衡器这2个模块还需要进一步研究和探讨.
| [1] |
刘海涛, 尹志胜, 张学军. 频率选择性瑞利衰落信道脉冲熄灭OFDM接收机差错性能分析[J]. 北京邮电大学学报, 2015, 38(4): 28–32.
Liu Haitao, Yin Zhisheng, Zhang Xuejun. Performance analysis of OFDM receiver with pulse blanking in frequency selective Rayleigh fading channel[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(4): 28–32. |
| [2] | Chen Sheng, Hanzo L, Livingstone A. MBER space-time decision feedback equalization assisted multiuser detection for multiple antenna aided SDMA systems[J]. Trans on Signal Processing, IEEE, 2006, 54(8): 3090–3098. doi: 10.1109/TSP.2006.877666 |
| [3] | Martin R K, Ysebaert G, Vanbleu K. Bit error rate minimizing channel shortening equalizers for cyclic prefixed systems[J]. IEEE Trans on Signal Processing, 2007, 55(6): 2605–2616. doi: 10.1109/TSP.2007.893913 |
| [4] |
邬正义, 朱仁祥, 吴乐南. 复值的MBER非线性均衡器用于QAM信号[J]. 信号处理, 2009, 25(12): 1956–1961.
Wu Zhengyi, Zhu Renxiang, Wu Lenan. Complex-valued minimum bit error rate nonlinear equalizers for QAM signals[J]. Signal Processing, 2009, 25(12): 1956–1961. |
| [5] | Schetzen M. The Volterra and Wiener theories of nonlinear systems[M]. New York: John Wiley and Sons, 1980: 85-116. |
| [6] | Zhou Dayong, Brunner D. Novel adaptive nonlinear predistorters based on the direct learning algorithm[J]. IEEE Transactions on Signal Processing, 2007, 55(1): 120–133. doi: 10.1109/TSP.2006.882058 |
| [7] | Eun C, Powers E J. A new Volterra pre-distorter based on the indirect learning architecture[J]. IEEE Trans on Signal Processing, 1997, 45(1): 223–227. doi: 10.1109/78.552219 |
| [8] | Laster D, Reed H, Tranter W H. Bit error rate estimation using probability density function estimators[J]. IEEE Trans on Vehicular Technology, 2003, 52(1): 260–267. doi: 10.1109/TVT.2002.807229 |


