提出了改进Polar码的最小和译码算法,修正了最小和译码算法中的节点更新公式,即利用分段线性函数来逼近置信度传播译码算法中的函数lncosh(x).相比于最小和译码算法,改进的算法在增加少许复杂度的情况下,增强了译码性能.相比于置信度传播译码算法,该算法在几乎不损失性能的情况下,大大降低了算法的计算复杂度,更易于硬件实现.该算法是基于最小和算法和置信度传播算法提出的,是在复杂度和性能上的一种折中.仿真结果表明,改进的最小和译码算法与置信度传播译码算法的性能几乎相同,比最小和译码算法的性能好.
In order to enhance the performance of the min-sum decoding algorithm for polar codes, an improved min-sum decoding algorithm was proposed. The improved method corrects the node update formulas of the min-sum decoding algorithm which replaces the function lncosh (x) in the belief propagation (BP) decoding algorithm with the piecewise linear approximation functions. Compared with the min-sum decoding algorithm, the modified decoding algorithm has better performance in case of increasing a little complexity. Compared with the BP decoding algorithm, the algorithm greatly reduces the computational complexity in case of almost no performance loss, and simplifies hardware implementation. The modified algorithm is based on the min-sum and the BP algorithms, and it is a compromise between the complexity and performance. Simulations show that the performance of the improved min-sum decoding algorithm is almost the same as the BP decoding algorithm, and better than the min-sum decoding algorithm.
Arikan[1]基于信道极化现象提出了Polar码的信道编码方法,该码是目前唯一被证明能达到容量限的码. Polar码在长码时性能良好,但是在中短码长时性能比低密度奇偶校验(LDPC,low density parity check) 码和Turbo码差,为了改善Polar码在有限码长时的性能,学者们提出了许多有效的改进方法[2-4].虽然置信度传播(BP,belief propagation) 译码算法具有较好的性能,但是其算法的复杂度较高,硬件实现较为复杂. Leroux等[5]提出了硬件上便于实现的Polar码最小和近似方法. Balatsoukas-Stimming等[6]也提到了这种最小和的近似方式来降低算法的复杂度.
最小和译码算法简化了BP译码算法的迭代更新公式,在性能方面有一定的退化,但是最小和译码算法计算复杂度低,硬件实现简单.笔者基于LDPC码的最小和译码算法的一些改进方案,提出了一种Polar码的改进的最小和译码算法,该算法修正了最小和译码算法中的迭代更新公式,用分段线性函数来代替最小和算法中的近似函数,即利用分段线性函数来逼近BP译码算法中的函数ln cosh (x),以减少最小和译码算法在简化BP译码算法后的性能损失,该算法在增加少许计算复杂度的条件下提高了算法的性能,是性能与计算复杂度的一个折中.
1 Polar码及其译码算法Polar码可看成是一个GN陪集码,可表示为(N, K, A, uAC),其中N为码长,可表示为N=2n,n为正整数,K为维数,也可看成是信息集合A的大小,A⊂{1, 2, …, N}.信息集合A的选取由信道极化决定,uAC表示固定比特,uAC∈XN-K.
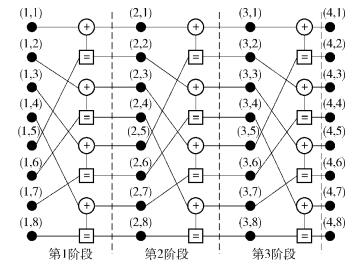
1.1 Polar码的BP译码算法Polar码的BP译码算法是基于Forney提出的码的因子图表示.一个(N, K) Polar码由一个n-阶段的因子图来迭代译码,因子图包括N(n+1) 个节点,每个节点由整数对(i, j) 表示,每个阶段包括N/2个处理单元(PE,processing element).节点(i, j) 的第1个元素表示阶层,第2个元素表示行,第1阶层的节点与信源矢量u有关,第n+1阶层的节点与码字有关.在整个译码器中,i和j的取值范围为0≤i≤n,0≤j≤N,在每个PE中,0≤i≤n,0≤j≤N/2. 图 1描述了n=3时Polar码的因子图表示,图 1中共有3个阶段,每个阶段包括4个PE,每个PE的信息传递过程如图 2所示.
|
图 1 n=3时Polar码的因子图表示 |
|
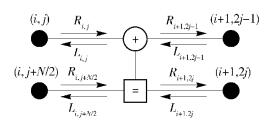
图 2 BP算法中PE的信息传递过程 |
在译码器的每个PE中,节点(i, j) 与2种类型的信息相关:从右到左的信息Li, j和从左到右的信息Ri, j. Li, j和Ri, j都是在相邻的节点间传递和迭代更新的,信息更新过程与文献[4]相同,信息首先从最右边的节点传到最左边的节点,然后从最左边的节点传到最右边的节点,这个过程就是BP译码算法中的一轮迭代.在迭代中,传递的信息都是对数似然比形式的,迭代公式为
| $ \begin{array}{l} {L_{i,j}} = g({L_{i + 1,2j - 1}},{L_{i + 1,2j}} + {R_{i,j + N/2}})\\ {L_{i,j + N/2}} = g({R_{i,j}},{L_{i + 1,2j - 1}}) + {L_{i + 1,2j}}\\ {R_{i + 1,2j - 1}} = g({R_{i,j}},{L_{i + 1,2j}} + {R_{i,j + N/2}})\\ {R_{i + 1,2j}} = g({R_{i,j}},{L_{i + 1,2j - 1}}) + {R_{i,j + N/2}}) \end{array} $ | (1) |
其中0≤i≤n, 0≤j≤N/2,且
| $ g({x_1},{x_2}) = 2{\rm{tan}}{{\rm{h}}^{ - 1}}({\rm{tanh}}({x_1}/2){\rm{tanh}}({x_2}/2)) $ |
或
| $ g({x_1},{x_2}) = {\rm{ln}}\;{\rm{cosh}}\left( {\frac{{{x_1} + {x_2}}}{2}} \right) - {\rm{ln}}\;{\rm{cosh}}\left( {\frac{{{x_1} - {x_2}}}{2}} \right) $ | (2) |
初始信息R1, j(0≤j≤N) 定义为
| $ {R_{1,j}} = \left\{ {\begin{array}{*{20}{c}} {0,}&{j \in A}\\ {\infty ,}&{j \in {A^C}} \end{array}} \right. $ | (3) |
来自于信道的信息Ln+1, j(0≤j≤N) 为
| $ {L_{n + 1,j}} = {\rm{ln}}\;\frac{{P({y_j}|{x_j} = 0)}}{{P({y_j}|{x_j} = 1)}} $ | (4) |
最小和译码算法是在BP译码算法的基础上改进的,其基础思想是对BP译码算法中更新规则中的式(2) 进行简化.当|x| > > 1时,ln cosh (x)≈|x|-ln 2,将其代入式(2),则式(2) 可简化为
| $ g({x_1},{x_2}) \approx {\rm{sgn}}({x_1}){\rm{sgn}}({x_2}){\rm{min}}(|{x_1}\left| , \right|{x_2}|) $ | (5) |
其中x1、x2为来自信道的对数似然比信息.从这个更新公式可以看出,最小和译码算法和BP译码算法的不同源于函数g(x1, x2) 的定义不同.
2 改进的最小和译码算法在文献[7]中,Park等修正了LDPC码的最小和译码算法,提高了算法的性能.笔者主要是基于这种思想,并改进了计算过程,将其应用到Polar码中,提出了一种改进的Polar码的最小和译码算法.
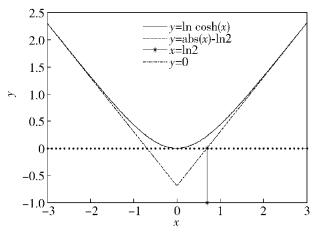
在BP译码算法中,令ln cosh (x)≈|x|-ln 2得出了最小和译码算法,但当|x| < 1时,ln cosh (x) 与|x|-ln 2的差别比较大,尤其当|x|=0时,ln cosh (x) 与|x|-ln 2的差值达到了ln 2(≈0.693),具体如图 3所示.
|
图 3 ln cosh (x) 的分段线性近似 |
由图 3可知,最小和算法在|x1+x2| < 2ln 2或|x1-x2| < 2ln 2时,将会导致性能的严重退化,为了增强最小和算法的性能,笔者提出了替代最小和算法中ln cosh (x)≈|x|-ln 2的分段函数为
| $ {\rm{ln}}\;{\rm{cosh}}\left( x \right) \approx \left\{ {\begin{array}{*{20}{l}} {0,{\rm{ }}\left| x \right| < {\rm{ln}}\;2}\\ {\left| x \right| - {\rm{ln}}\;2,{\rm{ }}\left| x \right| \ge {\rm{ln}}\;2} \end{array}} \right. $ | (6) |
将式(2) 中的函数ln cosh (x) 用式(6) 替代,则式(2) 转化为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g({x_1},{x_2}) \approx \\ \left\{ {\begin{array}{*{20}{l}} {0,{\rm{ }}|{x_1} + {x_2}| < 2{\rm{ln}}\;2,|{x_1} - {x_2}| < 2{\rm{ln}}\;2}\\ {{\rm{ln}}\;2 - \frac{{\left| {{x_1} - {x_2}} \right|}}{2},|{x_1} + {x_2}| < 2{\rm{ln}}\;2,|{x_1} - {x_2}| \ge 2{\rm{ln}}\;2}\\ {\frac{{|{x_1} + {x_2}|}}{2} - {\rm{ln}}\;2,{\rm{ }}|{x_1} + {x_2}| \ge 2{\rm{ln}}\;2,|{x_1} - {x_2}| < 2{\rm{ln}}\;2}\\ {{\rm{sgn}}({x_1}){\rm{sgn}}({x_2}){\rm{min}}(|{x_1}\left| , \right|{x_2}|),}\\ {|{x_1} + {x_2}| \ge 2{\rm{ln}}\;2,|{x_1} - {x_2}| \ge 2{\rm{ln}}\;2} \end{array}} \right. \end{array} $ | (7) |
其中x1, x2为来自信道的对数似然比信息,式(7) 即为改进的最小和译码算法的节点的更新公式.
笔者提出的Polar码的改进的最小和译码算法与BP及最小和译码算法的不同处只是迭代更新公式的计算方法不同,在改进的最小和译码算法中的节点更新规则传递信息的更新公式为
| $ {L_{i,j}} = g({L_{i + 1,2j - 1}},{L_{i + 1,2j}} + {R_{i,j + N/2}}) $ | (8a) |
| $ {L_{i,j + N/2}} = g({R_{i,j}},{L_{i + 1,2j - 1}}) + {L_{i + 1,2j}}) $ | (8b) |
| $ {R_{i + 1,2j - 1}} = g({R_{i,j}},{L_{i + 1,2j}} + {R_{i,j + N/2}}) $ | (8c) |
| $ {R_{i + 1,2j}} = g({R_{i,j}},{L_{i + 1,2j - 1}}) + {R_{i,j + N/2}}) $ | (8d) |
其中0≤i≤n,0≤j≤N/2,g(x1, x2) 由式(7) 定义.
改进的Polar码最小和译码算法的迭代方式和节点之间的迭代更新信息规则均与最小和译码算法及BP译码算法相同,其详细步骤如下.
1) 初始化:计算式(4) 中Ln+1, j的值作为初始信道信息,其中0≤j≤N;设定迭代次数T.
2) 当迭代次数小于T时:在每轮迭代中,首先,从因子图(见图 1) 中的第n阶段到第1阶段,在每个阶段的每个PEs (见图 2) 中,根据式(8a) 和式(8b) 更新每个节点的左信息Li, j;然后,从第1阶段到第n阶段,利用式(8c) 和式(8d) 更新各阶段中每个PEs的节点的右信息Ri, j.
3) 当达到迭代次数T时,进行比特判决,判决的依据是最后一轮迭代更新的左信息的值的大小.对于译码码字
笔者提出的Polar码的改进的最小和译码算法与最小和及BP译码算法相比,对ln cosh (x) 进行了替代,没有改变节点之间迭代更新规则以及算法的迭代次数等影响复杂度的因素,因此,改进的最小和译码算法与最小和译码算法及BP译码算法的时间复杂度一样,它们的计算复杂度的不同主要是由于节点的迭代更新公式的计算方法不同.因此对3种算法的计算复杂度的比较主要是对其迭代更新公式中函数g(x1, x2) 在计算复杂度上的比较.
从几个算法的更新公式g(x1, x2) 的定义中可以看出,在BP译码算法中,g(x1, x2) 的计算需要2次对数运算、2次双曲余弦函数计算、2次乘法运算和3次加法运算,运算复杂度是指数的,造成的时延较大,硬件实现上相对复杂;最小和译码算法中g(x1, x2) 的计算是最简单的,仅需要2次符号运算、2次取绝对值和1次比较得出最小值;而改进的最小和译码算法中最多需要2次加法、4次取绝对值、2次比较运算、2次符号运算,其运算复杂度低,时延较小,硬件实现上比较简单.
在以上3种译码算法的每轮迭代中的核心计算是节点更新公式的计算,且3种算法的译码流程是相同的,所以g(x1, x2) 的计算复杂度越低,则节点更新公式的计算复杂度也越低,其整个译码算法的计算复杂度也相应的越低.综上所述,笔者提出的译码算法的计算复杂度要比最小和译码算法略高,但比BP译码算法的计算复杂度低.
3.2 算法的仿真分析为了验证算法的性能,分别对改进的最小和译码算法、最小和译码算法和BP译码算法进行了对比性仿真实验.仿真中采用的信道都是二进制输入的加性高斯白噪声信道,调制方式是二进制相移键控调制,Polar码的码长N选取为256和1 024,码率为0.5,迭代次数设置为60次. Polar码的信息集合A是利用Tal-Vardy的方法来选取的[8].
表 1为在不同的信噪比下,改进的算法和最小和算法在节点更新公式中调用分段函数g(x1, x2) 各段所占的百分比.在表 1中,对于改进的算法的更新式(7),令调用g(x1, x2)=0时表示为情况1,调用g(x1, x2)=ln 2-|x1-x2|/2时表示为情况2,调用g(x1, x2)=|x1+x2|/2-ln 2时表示为情况3,调用g(x1, x2)=sgn (x1) sgn (x2) min (|x1|, |x2|) 时表示为情况4;在最小和算法的更新式(5) 中,相当于只调用了情况4.
|
|
表 1 改进算法及最小和算法调用g(x1, x2) 各段占比 |
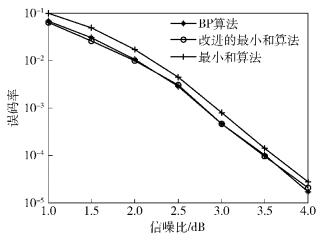
图 4比较了码长N为256时,Polar码的改进的最小和译码算法、最小和译码算法和BP译码算法的误码率性能.如图 4所示,相比于BP译码算法,当信噪比小于3 dB时,在相同的误码率下改进的最小和译码算法与BP译码算法的性能差距最多为0.05 dB,当信噪比大于3 dB时,改进的BP译码算法比BP译码算法的BER性能略差;改进的译码算法比最小和译码算法的性能好,当误码率为10-2时,改进的译码算法比最小和译码算法的性能好0.25 dB左右.当误码率为10-4时,改进的译码算法比最小和译码算法的性能好0.15 dB左右.
|
图 4 N=256 Polar码的3种译码算法的性能比较 |
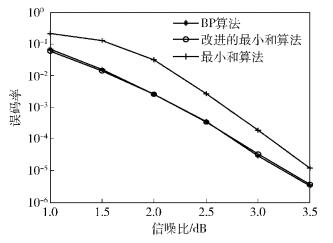
图 5比较了在码长N为1 024时,Polar码的改进的最小和译码算法、最小和译码算法和BP译码算法的误码率性能.从图 5可以看出,改进的算法与BP译码算法的性能差距最多在0.05 dB左右;改进的算法比最小和译码算法的性能要好,当误码率达到10-3时,改进的译码算法比最小和译码算法的性能好0.5 dB左右,当误码率达到10-5时,改进的译码算法比最小和译码算法的性能好0.25 dB左右.
|
图 5 N=1 024 Polar码的3种译码算法的性能比较 |
如表 1所示,在低信噪比时,改进的最小和算法调用情况1、情况2、情况3这3种情况所占的比例较高,而从图 4和图 5可知,在低信噪比时改进算法的性能明显优于最小和算法;随着信噪比的增加,改进的最小和算法调用情况4的比例在增加,从图 4和图 5可以看出,笔者提出的改进算法与最小和算法相比性能差别趋于变小,但仍具有明显优势.结合表 1、图 4和图 5可以得出,在改进迭代更新公式后,改进的算法相比于最小和译码算法,其性能有很大的提升,几乎与BP译码算法的性能相同.
4 结束语笔者提出了一种Polar码的改进的最小和译码算法,该算法修正了最小和算法中的迭代更新公式,用线性逼近函数来代替最小和算法中的近似函数,即利用分段线性逼近函数来代替BP译码算法中的函数ln cosh (x),以减少最小和译码算法近似后的性能损失.仿真结果表明,改进的算法相比于最小和算法增加了少许复杂度,但增强了算法的性能,且改进的算法与BP译码算法的性能几乎相同,而其计算复杂度大大低于BP译码算法.
| [1] | Arikan E. Channel polarization:a method for constructing capacity achieving codes for symmetric binary-input memoryless channels[J]. IEEE Trans Inf Theory, 2009, 55(7): 3051–3073. doi: 10.1109/TIT.2009.2021379 |
| [2] | Niu Kai, Chen Kai. Stack decoding of polar codes[J]. Electron Lett, 2012, 48(12): 695–696. doi: 10.1049/el.2012.1459 |
| [3] |
樊婷婷, 杨维, 许昌龙. Polar码SC译码算法的量化问题[J]. 北京邮电大学学报, 2015, 38(4): 95–100.
Fan Tingting, Yang Wei, Xu Changlong. The quantification problems for polar code with successive cancellation decoder algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(4): 95–100. |
| [4] | Zhang Yingxian, Liu Aijun, Pan Xiaofei, et al. A modified belief propagation polar decoder[J]. IEEE Commun Lett, 2014, 18(7): 1091–1094. doi: 10.1109/LCOMM.2014.2316365 |
| [5] | Leroux C, Raymond A J, Sarkis G, et al. Hardware implementation of successive cancellation decoders for polar codes[J]. J Sign Process Syst, 2012, 69(3): 305–315. doi: 10.1007/s11265-012-0685-3 |
| [6] | Balatsoukas-Stimming A, Parizi M B, Burg A. LLR-based successive cancellation list decoding of polar codes[J]. IEEE Trans Signal Process, 2015, 63(19): 5165–5179. doi: 10.1109/TSP.2015.2439211 |
| [7] | Park S I, Kim H M, Kim J. Enhanced min-sum decoding for DVB-T2 LDPC codes[C]//ICCE 2013. Las Vegas:IEEE, 2013:576-577. |
| [8] | Tal I, Vardy A. How to construct Polar code[J]. IEEE Trans Inf Theory, 2013, 59(10): 6562–6582. doi: 10.1109/TIT.2013.2272694 |


