2. 北京邮电大学 自动化学院, 北京 100876
为解决具有灰度不均匀、低对比度以及边缘模糊等缺陷的粘连细胞分割问题,提出结合水平集方法的轮廓提取和凹点区域检测的细胞分割方法.利用水平集方法可很好地解决曲线演化过程中的拓扑变化问题,结合细胞图像的区域信息和边缘信息,能有效提取细胞的边缘轮廓.该方法可最大限度地保留细胞边缘轮廓的几何特征.根据多边形的凹凸性,循环迭代检测粘连细胞轮廓上的凹点区域,确定细胞的粘连位置,最后确定粘连位置的分割连接线.对几十幅不同粘连细胞图像的分割实验结果表明,该方法易于实现,鲁棒性强,效果明显,细胞分割的平均准确率达到83.01%,优于分水岭及聚类分割方法.
2. Automation School, Beijing University of Posts and Telecommunications, Beijing 100876, China
Overlapping cell images with inhomogeneity intensity, low contrast and edge blurring are difficult to be segmented. The author proposes a new cell segmentation algorithm combining level set method and concave area detection. First, the level set method can easily handle topology changes of the evolving contour. And it can be employed to obtain the cell profile, combined with the regional information and edge information. This step keeps the geometric characteristics of the cell profile effectively. Second, the concave area of overlapping contour location based on the concave and convex of polygons was searched for. Finally, the splitting line of overlapping cells at the location of concave area was determined. Experiments on dozens of different overlapping cell images segmentation show that the algorithm is robust, effective and easy to implement. The average accuracy of cell segmentation reaches to 83.01%, which is superior to the results of the watershed and k-means clustering methods.
图像分割是医学图像处理和分析的关键,而粘连细胞图像的分割是其中的难点和热点问题.由于图像中常常存在灰度不均匀、低对比度以及边缘模糊等缺陷[1],给粘连细胞的分割带来困难,也对算法的鲁棒性提出了挑战.
基于细胞图像的边缘、纹理、灰度等视觉特征,学者们提出了诸如分水岭[2]、链码法、聚类[3]、水平集方法[4]和凹点法[5]等算法.凹点法是细胞分割中比较常见的分割算法,主要是将检测细胞粘连处的凹陷点作为分割依据,其主要存在两个缺陷:① 不能有效提取粘连细胞图像的边缘轮廓,常用算法针对单像素的边缘,影响凹点位置检测;② 不能准确找到细胞粘连的凹点位置.
针对凹点法的缺陷,笔者提出了基于水平集方法的边缘轮廓提取和凹点区域检测相结合的细胞图像分割方法.采用基于亚像素级的细胞边缘轮廓,利用边缘轮廓循环迭代搜索能够有效克服噪声点对凹点检测准确度的影响.首先,针对图像的灰度不均匀、低对比度以及边缘模糊等特征,使用基于区域信息与边缘信息相结合的水平集方法,在最大限度地保留细胞几何特征的情况下,有效提取细胞的边缘轮廓;然后,根据多边形的凹凸性,循环迭代搜索检测粘连细胞轮廓上的凹点区域,确定细胞的粘连位置;最后,应用路径匹配规则,确定分割凹点位置,实现粘连细胞分割.
1 轮廓提取由于乳腺显微组织细胞图像在制作过程中受到光照、设备精度等因素影响,存在灰度不均匀、低对比度以及边缘模糊等缺陷,传统基于边缘检测类的算法无法有效提取细胞的边缘轮廓.因此,采用基于水平集方法的活动轮廓模型,利用其可以灵活地添加正则化项进行约束的优势,将基于区域信息和边缘信息的轮廓检测算法结合在一起.该算法在充分保留细胞边缘几何特征的情况下,有效提取细胞的边缘轮廓,同时,在一定程度上保持细胞轮廓的平滑性.
水平集方法的基本思想是引入偏微分方程,利用水平集方法将n维空间的演化问题表达为n+1维空间的高维演化问题.将活动轮廓模型转化为求解最小化能量泛函的形式,可以有效解决在曲线演化过程中拓扑结构变化的问题.将闭合曲线C∈Ω用水平集表示:C(t)={(x, y)∈Ω|φ(x, y, t)=0}.那么,初始化的零水平集函数所对应的符号距离函数表示为
| $ \phi \left( {x,y,t = 0} \right) = \pm d $ | (1) |
通常定义闭合曲线里面为负数,外面为正数. d表示的是点(x, y) 到曲线C的最短距离.
将图像看作分段常数模型,并引入正则化项Heaviside函数和Dirac函数,表达式为
| $ {H_\varepsilon }\left( \phi \right) = \frac{1}{2}\left( {1 + \frac{2}{{\rm{\pi }}}{\rm{arctan}}\left( {\frac{\phi }{\varepsilon }} \right)} \right) $ | (2) |
| $ {\delta _\varepsilon }\left( \phi \right) = \frac{{\rm{d}}}{{{\rm{d}}\phi }}{H_\varepsilon }\left( \phi \right) = \frac{1}{{\rm{\pi }}}\frac{\varepsilon }{{{\varepsilon ^2} + {\phi ^2}}} $ | (3) |
其中ε为Heaviside函数的调节参数,在本算法中取值为1.
结合图像的区域信息和边缘信息,对细胞边缘轮廓的提取等价于求解如下能量泛函关于φ(x, y) 的最小值:
| $ \begin{align} & E={{\lambda }_{a}}\iint_{\Omega }{|I\left( x,y \right)-{{c}_{a}}{{|}^{2}}}H\left( \phi \left( x,y \right) \right)\text{d}x\text{d}y+ \\ & {{\lambda }_{b}}\iint_{\Omega }{|I\left( x,y \right)-{{c}_{b}}{{|}^{2}}}\left( 1-H\left( \phi \left( x,y \right) \right) \right)\text{d}x\text{d}y+ \\ & \ \ \ \mu \iint_{\Omega }{g\delta \left( \phi \left( x,y \right) \right)}|\nabla \phi \left( x,y \right)|\text{d}x\text{d}y \\ \end{align} $ | (4) |
其中:λa、λb和μ为取值为正的常数,一般情况下可固定λa=λb=1. ca为曲线内的灰度均值,cb为曲线外的灰度均值,g为边缘检测算子函数,I(x, y) 为分段光滑图像.在演化过程中,曲线C会不断地发生变化,每次演化后,固定函数φ,重新计算曲线内外的灰度均值ca和cb,其更新方程为
| $ {{c}_{a}}=\frac{\iint_{\Omega }{I\left( x,y \right)}H\left( \phi \left( x,y \right) \right)\text{d}x\text{d}y}{\iint_{\Omega }{H\left( \phi \left( x,y \right) \right)}\text{d}x\text{d}y} $ | (5) |
| $ {{c}_{b}}=\frac{\iint_{\Omega }{I\left( x,y \right)}\left( 1-H\left( \phi \left( x,y \right) \right) \right)\text{d}x\text{d}y}{\iint_{\Omega }{H\left( \phi \left( x,y \right) \right)}\text{d}x\text{d}y} $ | (6) |
固定ca和cb的值,利用梯度下降流法求解能量泛函的数值解,其偏微分方程的表达式为
| $ \begin{array}{l} \frac{{\partial \phi }}{{\partial t}} = \delta \left( \phi \right)\left\{ {{\lambda _a}} \right.{(I - {c_a})^2} - {\lambda _b}{(I - {c_b})^2} + \\ \mu \nabla g\frac{{\nabla \phi }}{{|\nabla \phi |}} + \gamma g{\rm{div}}\left. {\left( {\frac{{\nabla \phi }}{{|\nabla \phi |}}} \right)} \right\} \end{array} $ | (7) |
其中γ是常数,为0.2.采用水平集方法的活动轮廓模型提取细胞边缘轮廓,实质是构造基于边缘与区域信息相结合的能量函数.通过梯度下降流求解最小化能量泛函,驱使曲线逐渐演化到细胞的边缘轮廓位置.利用水平集方法的活动轮廓模型使得演化后的边缘是闭合且平滑的轮廓,这对粘连细胞的凹点区域检测很有利.
2 凹点区域检测轮廓上的凹凸点是多边形十分重要的特征信息.通常,2个细胞的粘连位置会有明显的深度凹点区域,寻找并定位这些凹点区域,可以作为粘连细胞分割的重要依据.谢忠红等[6]通过计算N点方向编码差定位分割凹点群,利用凹点群中凹点凹度最深的点来确定分割凹点位置,该算法中步长N选取的大小会对精度产生一定的影响.
针对N点方向编码差寻找粘连处最凹点可能不准确的问题,提出一种凹点区域检测方法,其基本思想:首先,将封闭细胞轮廓视作多边形,并将细胞轮廓描述为有序的坐标点集;然后,判断轮廓上各点的凹凸性,提取轮廓上的所有凹点构成新的多边形,对新的多边形再判断凹点并提取凹点集,如此循环搜索,直到找到可用于分割的凹点区域;最后,寻找最佳的粘连分割线.凹点区域检测过程回避了步长设置,采用循环搜索的方法,精度上有较大提高.
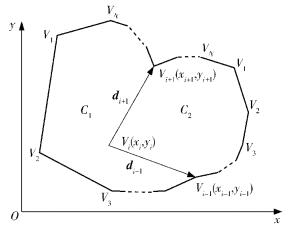
判断细胞轮廓多边形上点的凹凸性的方法如下.按照逆时针方向,定义粘连细胞轮廓Ck上的描述点依序为{V1, …Vi, …, VN},i为轮廓上像素点的索引值.则Vi=(xi, yi) 与其前序点Vi-1=(xi-1, yi-1) 和后序点Vi+1=(xi+1, yi+1) 构成的方向向量分别为di-1与di+1,如图 1所示.
| $ \left. \begin{array}{l} {\boldsymbol{d}_{i - 1}} = {V_{i - 1}} - {V_i} = ({x_{i - 1}} - {x_i},{y_{i - 1}} - {y_i})\\ {\boldsymbol{d}_{i + 1}} = {V_{i + 1}} - {V_i} = ({x_{i + 1}} - {x_i},{y_{i + 1}} - {y_i}) \end{array} \right\} $ | (8) |
|
图 1 细胞轮廓多边形上点的凹凸性判断示意图 |
根据多边形的凹凸性,在凹点和凸点处存在不同的符号函数sign (Di),从而利用符号函数来判定凹点和凸点.其中:
| $ {\rm{sign}}({D_i}) = \left\{ {\begin{array}{*{20}{c}} {1,}&{{D_i} > 0}\\ {0,}&{{D_i} \le 0} \end{array}} \right. $ | (9) |
Di值的计算方法为
| $ {D_i} = ({\boldsymbol{d}_{i - 1}} \times {\boldsymbol{d}_{i + 1}})\cdot n,{\rm{ }}i = \left( {1,2, \ldots ,N} \right) $ | (10) |
其中n为平面法向量.当sign (Di)=1时,Vi表示多边形的凹点;当sign (Di)=0时,Vi表示多边形的凸点.从而,多边形轮廓上所有点的凹凸性均可根据式(9) 判断.举例说明,如图 1所示,在多边形轮廓C1上,Di=(di-1×di+1)·n的值大于0,表示Vi点为凹点;而在多边形轮廓C2上,Di=(di+1×di-1)·n的值小于0,表示Vi点为凸点.
通过对大量实际细胞图像的分割实验发现了细胞粘连最常出现的5种情形,如图 2所示.下面重点讨论这5种凹点区域的检测情况.

|
图 2 5种常见的细胞粘连情况 |
凹点区检测和细胞分割可利用细胞面积的先验知识有效降低算法的计算量,同时提高细胞分割的准确率.通过面积约束,可以滤除部分单细胞轮廓上的凹点搜索.由水平集提取的细胞边缘轮廓为平滑边缘轮廓,轮廓包含单个细胞的边缘轮廓和粘连细胞的边缘轮廓.根据细胞面积的统计特性设定单个细胞面积阈值为AC(或者设定单细胞周长阈值).当轮廓C包围的面积小于AC时,认为其为单细胞;当轮廓C包围的面积大于AC时,便认为其为粘连细胞.
利用循环搜索的方法检测细胞粘连的凹点区域.经过若干轮凹点区域循环搜索后,粘连细胞轮廓的凹点会集中在深凹区域内.凹点区域内的凹点是沿着边缘轮廓线集中分布在某一段相邻像素点内,因此,通过设定轮廓线上相邻T个像素点所具有的凹点数不小于GT作为判断凹点区域的依据.凹点区域检测算法的迭代求解过程如下:
1) 单幅图像经过水平集演化后,提取每个细胞轮廓,记作Cs (s=1, …, s, …, S).
2) 计算每个细胞轮廓的面积,提取面积大于阈值AC的K(K≤S) 个细胞轮廓,则任一粘连细胞轮廓Ck的点集依逆时针序描述为Ck={V1, …, Vi, …, VN},i为轮廓上像素点的索引值.
3) 对多边形轮廓上的每一像素点i,求取其符号函数sign (Di) 值,当sign (Di)=1时Vi为凹点,当sign (Di)=0时Vi为凸点.
4) 存储多边形上所有凹点,将其表示为M={m1, …, mj, …, mL},L < N.
5) 判断轮廓线上T个相邻像素点中的凹点数是否大于GT,当检测的凹点个数大于GT时,表示该点集为凹点区域;否则为非凹点区域.
6) 统计轮廓上凹点区域数量,当检测到凹点区域个数为0时,停止迭代,默认为单细胞,不分割.当满足表 1所示的任何一种情况时,终止迭代,凹点区域检测完成;否则,用凹点集M构建新的多边形轮廓,跳转至第3) 步.
|
|
表 1 粘连细胞凹区数及可分割细胞数 |
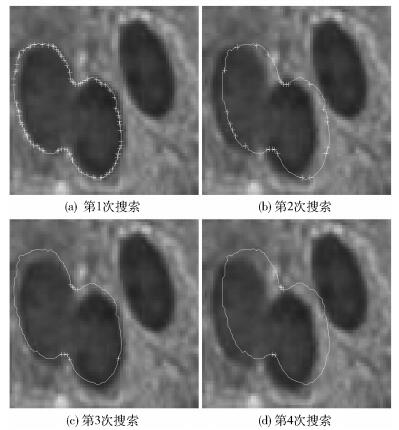
通过以上步骤迭代寻找细胞轮廓上的凹点区域,如图 3所示.经过4次迭代搜索,可以检测出有2个凹点区域并精确定位.
1) 图 2(a)情况:当有1个凹点区域时,选取凹点区域所在轮廓线上的中间点位置,计算其与轮廓上每个点的欧氏距离,选取其中最长的分割线作为粘连分割线.
|
图 3 凹点区域检测及定位的迭代搜索过程示意图(“+”表示凹点) |
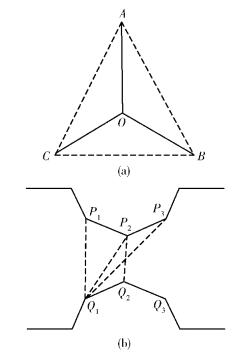
2) 图 2(c)情况:由3个凹点区域所在轮廓线上的中间点位置构成三角形,计算这个三角形重心,然后将三角形区域的重心与凹点区域所在轮廓线上的中间点相连接构成粘连细胞的轮廓分割线,如图 (4a)所示.
|
图 4 典型粘连情况下细胞分割线的确定示意图 |
3) 图 2(b)(d)(e)情况可视作同一类分割问题.笔者认为在粘连处,距离最短的凹点对就是分割粘连细胞的最佳位点.如图 4(b)所示,P1、P2、P3和Q1、Q2、Q3分别为对应的凹点区域的凹点,分别计算P1、P2、P3到Q1、Q2、Q3三个点的欧氏距离,然后取9条线段中最短的路径定义为分割线.显然,P2到Q2的距离最短,从而P2Q2即为分割线.
3 实验结果与分析 3.1 实验数据实验数据分为两部分:第1部分为合成图像数据,主要是验证图像对噪声干扰的鲁棒性,并展示多粘连情况下的分割效果;第2部分采用乳腺显微组织细胞图像,该图像存在灰度不均匀性、低对比度以及边缘模糊等特性,传统基于边缘检测类算法无法准确提取细胞的边缘轮廓.下面分别用合成图像和真实细胞图像对所提出的方法进行验证.
3.2 合成图像分割合成图像分割主要是验证新方法对噪声和多粘连图像的分割效果. 图 5(a)是多粘连、灰度不均匀的合成图像,实验过程中的面积阈值AC设置为100. 图 5(b)是用水平集方法迭代70步提取的边缘轮廓,轮廓具有良好的光滑性,这对凹点的准确提取十分有利.尽管细胞粘连数量多,但在凹点搜索时只进行4次循环搜索,分割效果如图 5(c)所示.

|
图 5 粘连图像的局部分割效果图 |
由于真实细胞图像在制作过程中受到光照、设备精度等因素影响,常常出现灰度不均匀、低对比度以及边缘模糊等特性,下面利用所提方法对乳腺显微组织细胞图像进行分割,从而验证算法的有效性和鲁棒性. 图 5(d)是3个细胞粘连图像,存在灰度不均匀、低对比度以及边缘模糊等缺陷. 图 5(e)是利用所提出的方法得到的粘连细胞轮廓,实验过程中,水平集迭代次数为300步.由于本实验中图像的分辨率高,面积阈值AC设置为400.凹点搜索迭代的次数为6次,再确定细胞的最佳分割位置,如图 5(f)所示,粘连细胞分割效果十分明显.
为进一步说明所提方法的有效性,对真实细胞图像进行分割,将所提方法与常用的聚类算法和分水岭算法进行对比.在实验中,对40幅真实的粘连细胞子图进行分割,然后与基准图(由病理学家手工标记) 进行对照,根据专家经验统计准确分割细胞的数量.计算每种分割算法在实验过程中所得准确率的最大值和最小值.最后统计3种算法在分割40幅子图共1 943个细胞时的平均准确率.细胞分割的准确率计算公式为
| $ 准确率 = \frac{单幅子图上准确分割细胞数量}{单幅子图上的细胞总数} \times 100\% $ | (11) |
实验统计结果如表 2所示.由表 2可见,对于细胞粘连位置处有明显凹陷区域的子图,所提方法准确率可达90.91%,对于粘连严重、边缘模糊的子图,所提方法准确率降低为76.11%,但均优于对比方法.这是因为聚类算法基于像素点按照一定规则进行分类进而实现分割,对于粘连细胞容易引起欠分割且对噪声敏感.由于图像灰度不均匀,分水岭算法也易导致欠分割,从而使得准确性较低.
|
|
表 2 3种算法分割粘连图像的准确率对比 |
提出一种结合水平集轮廓提取和凹点区域检测的粘连细胞分割新方法.与传统的边缘检测方法相比,基于水平集的轮廓提取方法可有效克服图像的灰度不均匀、低对比度和边缘模糊等因素的影响.凹点区域检测算法则通过判断细胞轮廓点集的凹凸性以及多轮凹点区域搜索,从而检测并定位分割粘连细胞的凹点对,最终准确、有效地分割粘连细胞.
| [1] |
李叶舟, 胡静, 牛少彰, 等. 基于光照方向不一致的图像盲取技术[J]. 北京邮电大学学报, 2011, 34(3): 26–30.
Li Yezhou, Hu Jing, Niu Shaozhang, et al. Exposing digital image forgeries by detecting inconsistence in light source direction[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(3): 26–30. |
| [2] | Felix B, Carsten M, Michael S, et al. An automatic method for robust and fast cell detection in bright field images from high-throughput microscopy[J]. BMC Bioinformatics, 2013(14): 297–310. |
| [3] | Chitade A Z, Katiyar S K. Colour based image segmentation using k-means clustering[J]. International Journal of Engineering Science and Technology, 2010, 2(10): 5319–5325. |
| [4] | Dzyubachyk O, Van Cappellen W, Essers J, et al. Advanced level set-based cell tracking in time-lapse fluorescence microscopy[J]. IEEE Transactions on Medical Imaging, 2010(29): 852–867. |
| [5] | Duartea M, Alvarenga A, Azevedo C, et al. Evaluating geodesic active contours in microcal-cifications segmentation on mammograms[J]. Computer Methods Programs Biomedical, 2015(3968): 1–12. |
| [6] |
谢忠红, 姬长英, 郭小清, 等. 基于凹点搜索的重叠果实定位检测算法研究[J]. 农业机械学报, 2011, 42(12): 191–196.
Xie Zhonghong, Ji Changying, Guo Xiaoqing, et al. Detection and location algorithm for overlapped fruits based on concave spots searching[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(12): 191–196. |


