为建立超大容量通信系统提供全新的理论依据,证明了在高斯白噪声干扰环境下,当信道传输函数H(f)的单边带宽限定为B时,仙侬仅利用时间域间隔为1/2B的独立样点荷载信息是不够的,还应该根据重叠复用原理,同时使用频率域间隔为B/K独立样点的重叠频域复用技术,使系统容量与K成正比.由于带宽为B信道冲击响应的持续时间T趋近于无穷,频率域独立样点间隔1/T为0,K不受限制;同理,当信道冲激响应函数h(t)的持续时间限定为T时,像正交频分复用那样仅利用频率域间隔为1/T的独立样点去荷载信息是不够的,还应该根据重叠复用原理,用时间域间隔为T/K独立样点的重叠时域复用技术,使系统容量与K成正比.由于冲击响应持续时间为T信道的带宽B趋近于无穷,时间域独立样点间隔1/2B为0,所以K不受限制.此外,还证明了重叠复用的实质是建立超大容量的独立并联高斯信道.
In order to offer a new theoretical foundation for constructing huge capacity communication system without increasing system bandwidth, it has been verified that under additive white Gaussian noise environment, if the transfer function H(f) of the channel has a limited bandwidth B (single side), the duration T of the impulse response function h(t) goes to infinite, the space between independent samples are 1/2B and 0 respectively in time and frequency domain. It is not sufficient to only employ independent signaling samples separated by 1/2B Sec in time domain like Shannon, it should be also to employ independent signaling samples separated by B/K Hz in frequency domain. In this way, the channel capacity is proportional to K. Since the space between independent samples is 0 in frequency domain, K has no limited. The Shannon capacity is only a special case of ignoring the independent signaling samples in frequency domain (K=1). Similarly if the impose response function h(t) of the channel has a limited time duration T, the bandwidth B of the transfer function H(f) goes to infinite, the space between independent samples are 0 and 1/T respectively in time and frequency domain. It is not sufficient to only employ independent signaling samples separated by 1/T Hz in frequency domain like orthogonal frequency division multiplexing, it should be also to employ independent signaling samples separated by T/K Sec in time domain. Similarly, the channel capacity is proportional to K. Since the space between independent samples is 0 in time domain, K has no limited. And the essential of overlapped multiplexing principle is to construct independent parallel Gaussian channels.
通信系统与运输系统的实质是一致的,只不过通信系统搬运的是数据比特,运输系统搬运的是货物.在给定搬运速度和道路的条件下,运输系统的牵引功率至多随其搬运“容量”(单位为t/h) 呈线性关系.但根据仙侬(Shannon 1948) 信息论,单信道通信系统的发射功率在给定带宽和噪声环境下(相当于运输系统的道路条件) 却至少要随其搬运容量(单位为bit/s) 呈指数关系(其搬运速度在真空与大气中为光速).为什么实质相同的2个系统间会有如此巨大差异?
基本信息论[1]告诉我们:在高斯噪声环境下,独立并联高斯信道具有最大的容量和频谱效率,其系统容量和频谱效率等于各子信道之和,其容量、频谱效率与接收信噪比(正比于总发射功率) 呈线性关系.多输入多输出(MIMO, multiple input and multiple output) 系统是至今为止唯一发现的独立并联高斯信道传输系统,但它不是单信道传输系统.有没有只使用单信道传输但本质却是独立并联高斯信道的传输系统呢?笔者将试图解决这个问题,并给出其信道容量.
在高斯噪声干扰环境下,现有复用技术都形成不了独立并联高斯信道传输系统,如时分复用(TDM, time division multiplexing)、正交时分复用(OTDM, orthogonal time division multiplexing)、频分复用(FDM, frequency division multiplexing)、正交频分复用(OFDM, orthogonal frequency division multiplexing) 等.因为它们的子信道高斯噪声的独立性是因处于不同时频空间所形成的.虽然它们的系统容量都等于各子信道系统容量之和,但却是依赖分配信道容量的正交分解而来,系统容量与频谱效率毫无变化,当然不属于真正的独立并联高斯信道传输系统;另外,虽然码分复用(CDM, code division multiplexing) 与码分多址(CDMA, code division multiple access) 的子信道占据的是相同的时频空间,但它们的高斯噪声不独立.子信道容量和频谱效率随着其子信道数增加反而下降,系统容量和频谱效率只稍有增长.它们基本也属于分配信道容量与频谱效率的并行传输系统,也不是真正的独立并联高斯信道传输系统.真正独立并联高斯信道必须具有以下2个最基本的特点:
1) 各子信道有独立的高斯噪声;
2) 全部子信道占据相同的时频空间.
此外还必须具有以下4个特点:
1) 接收信扰比等于各子信道信扰比之和;
2) 系统容量(频谱效率) 等于各子信道的之和;
3) 系统容量(频谱效率) 随接收信噪比线性增长;
4) 系统有极高的容量(频谱效率).
重叠复用原理(overlapped multiplexing principle) 是笔者发现的一个新原理,笔者认为:在数据通信系统中,相连与相邻数据符号间的重叠绝不是干扰而是有益的编码约束关系,重叠越严重,编码增益越高.只有系统外部来的破坏性因素才是干扰.根据该原理,笔者摈弃了全部基于正交分解分配信道容量的复用理论和技术,改用全新的重叠复用理论和技术,在文献[2-3, 5]中分别提出了时间域的重叠复用理论与技术(OVTDM, overlapped time domain multiplexing) 及频率域的重叠复用理论与技术(OVFDM, overlapped frequency domain multiplexing). OVTDM利用持续时间T有限的信道冲击响应函数h(t) 作移位重叠复用(并行传输),其移位间隔可以远小于T,这样虽然在其传输信号中造成严重的重叠,但却极大提高了系统容量和频谱效率;OVFDM利用带宽B有限的信道传输函数h(t) 作移位重叠复用(并行传输),其移位间隔可以远小于带宽B,这样,虽然在其系统传输信号中造成严重重叠,但却极大提高了系统容量与频谱效率.由于时间域与频率域是对偶关系,当h(t) 与H(f) 波形相同时,二者的性能完全一致,故统称之为OVXDM.显然,X除了可以代表时间域T、频率域F以外,也可扩展到其他域.文献[2-3, 5]中的理论分析与长达十余年数百人次的大量独立反复验证发现,OVXDM的确有极为优良的性能,其信扰比与系统容量(频谱效率) 间不是仙侬指出的指数而是线性关系.那么OVXDM是否属于单信道传输的独立并联高斯信道传输技术呢?
众所周知,信道的传输函数H(f) 与对应的冲击响应函数h(t) 是一对傅氏变换关系,表示为H(f)↔h(t).在高斯噪声环境下,当信道传输函数H(f) 的带宽严格限定为B (单边) 时,其对应信道冲击响应函数h(f) 可被间隔为1/2B的独立样点序列所描述,著名仙侬信道容量公式C=Blb (1+SNR) 就是在此条件下导出的,OTDM与FTN (fast than Nyguist) 也是在此条件下建立起来的.同样,当信道冲击响应函数H(f) 的持续时间严格限定为T时,其对应信道传输函数H(f) 可被间隔为1/T Hz的独立样点序列所描述,OFDM与非正交频率分割复用(NOFDM, non-orthogonal frequency division multiplexing) 就是在此条件下建立的.
OVFDM的建立条件也是假定信道传输函数H(f) 的带宽严格限定为B赫兹(单边),但与OTDM和FTN仅使用时间域样点有本质不同,因为带宽B有限信道传输函数H(f) 所对应的信道冲击响应函数h(t) 的持续时间T一定趋近无穷. OVFDM除了利用间隔为1/2B的时间域独立样点传输数据以外,还主要利用了频率域移位的H(f) 作为传输数据的载体.由于此时频率域独立样点的间隔1/T趋近于零,所以尽管众多频率域移位的H(f) 造成了严重的重叠,但却等效于频率域独立采样,恰恰正是这种增加的频率域独立样点大幅度提高了OVFDM的系统容量与频谱效率.而且由于频率域独立样点的间隔1/T趋近于零,无论多高的频率域采样率都属于欠采样.
OVTDM的建立条件也是假定信道冲击响应函数h(t) 的持续时间严格限定为T s,但与OFDM及NOFDM仅使用频率域样点有本质不同,因为持续时间严格有限的信道冲击响应h(t)) 所对应的信道传输函数H(f) 的占据带宽B一定趋近无穷. OVTDM除了利用间隔为1/T的频率域独立样点传输数据以外,还主要利用了时间域移位的h(t)) 作为传输数据的载体,由于此时时间域独立样点的间隔1/2B趋近于零,所以尽管众多时间域移位的h(t)) 造成了严重的重叠,但却等效于在时间域独立采样,恰恰是这增加的时间域独立样点大幅度提高了OVTDM的系统容量和频谱效率.而且由于时间域独立样点的间隔1/2B趋近于零,无论多高的时间域采样率都属于欠采样.
OVXDM是否在实质上属于单信道传输的独立并联高斯信道?文献[2-3, 5]中的理论分析和大量独立仿真结果都证明了OVXDM有极高的系统容量与频谱效率,OVXDM系统的门限信扰比只大体随信道容量与频谱效率线性增长,其系统容量与频谱效率只受接收总信扰比的限制,这些都与独立并联高斯信道或MIMO一致.在高斯白噪声环境下,OVXDM的性质的确是一种独立并联高斯信道传输系统. MIMO子信道的独立性主要是由子信道的独立复高斯衰落与独立高斯噪声形成,OVXDM子信道的独立高斯性是从何而来的呢?笔者首先证明OVXDM隐含多个并行独立高斯子信道,其各子信道的独立性,是由其输入数据的独立性与其子信道高斯噪声独立性共同形成的.最后利用信道输出输入之间的最大互信息求解出了重叠复用原理下OVTDM与OVFDM在加性白高斯噪声(AWGN, additive white gaussian noise) 信道的容量,可发现:根据重叠复用原理建立的OVXDM重叠复用信道容量的确只随接收信噪比呈线性而不是仙侬指出的对数关系!这就为建立超大容量的通信系统提供了全新的理论基础[6].
1 经典独立并联高斯信道模型与若干基本关系回顾 1.1 经典独立并联高斯信道模型根据Cover[1],经典独立并联高斯信道的模型如图 1所示.各子信道的输出Yk是其输入Xk与高斯随机噪声Zk之和.对于第k(k=0, 1, …, K-1) 子信道,其输出Yk为Yk=Xk+Zk.其中Zk是均值为0、方差(功率) 为PN, k的独立高斯噪声,即
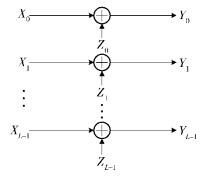
|
图 1 并联高斯信道模型 |
| $ E\{ {Z_k}\} = 0,{\rm{ }}E\{ {Z_k}{Z_{k\prime }}\} = {P_{N,k}}{\delta _{k,k\prime }} $ | (1) |
Xk是均值为0,相互独立,并与Zk独立的信道输入随机变量,其功率为Ps, k=E{Xk2}.
| $ E\{ {X_k}\} = 0,{\rm{ }}E\{ {X_k}{X_{k\prime }}\} = {P_{s,k}}{\delta _{k,k\prime }},{\rm{ }}E\{ {X_k}{Z_{k\prime }}\} = 0 $ | (2) |
则信道容量CK为最大互信息:
| $ {C_K} = \mathop {{\rm{max}}}\limits_{P({X_0},{X_1}, \cdots ,{X_{K - 1}})} I({X_0},{X_1}, \cdots ,{X_{K - 1}};{Y_0},{Y_1}, \cdots ,{Y_{K - 1}}) $ | (3) |
其中P(X0, X1, …, XK-1) 是(X0, X1, …, XK-1) 的联合分布.
独立并联高斯信道容量CL的证明除了仅仅利用了独立性外,其他步骤与证明单一高斯信道容量时完全类似[1],现简略证明如下:
令I(X0, X1, …, XK-1; Y0, Y1, …, YK-1) 表示2个随机序列(X0, X1, …, XK-1) 和(Y0, Y1, …, YK-1) 之间的互信息.
h(X0, X1, …, XK-1) 表示随机序列X0, X1, …, XK-1的熵.
h(Y0, Y1, …, YK-1/X0, X1, …, XK-1) 表示序列Y0, Y1, …, YK-1的条件熵.
两随机序列(X0, X1, …, XK-1), (Y0, Y1, …, YK-1) 之间的互信息为
| $ \begin{array}{l} I({X_0},{X_1}, \cdots ,{X_{K - 1}};{Y_0},{Y_1}, \cdots ,{Y_{K - 1}}) = {\rm{ }}h({Y_0},{Y_1}, \cdots ,\\ \;\;\;{Y_{K - 1}}) - h({Y_0},{Y_1}, \cdots ,{Y_{K - 1}}/{X_0},{X_1}, \cdots ,{X_{K - 1}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;h({Y_0},{Y_1}, \ldots ,{Y_{K - 1}}) - \\ \;\;\;\;\;\;\;\;\;\;\;h({Z_0},{Z_1}, \cdots ,{Z_{K - 1}}/{X_0},{X_1}, \cdots ,{X_{K - 1}}) \end{array} $ | (3) |
根据随机变量Xk与Zk的独立性,有
| $ \begin{array}{l} h({Z_0},{Z_1}, \cdots ,{Z_{K - 1}}/{X_0},{X_1}, \cdots ,{X_{K - 1}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;h({Z_0},{Z_1}, \cdots ,{Z_{K - 1}}) \end{array} $ | (4) |
| $ \begin{array}{l} \;\;\;\;I({X_0},{X_1}, \cdots ,{X_{L - 1}};{Y_0},{Y_1}, \cdots ,{Y_{L - 1}}) = \\ \;\;h({Y_0},{Y_1}, \cdots ,{Y_{L - 1}}) - h({Z_0},{Z_1}, \cdots ,{Z_{L - 1}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 0}^{L - 1} {h({Y_l})} - \sum\limits_{l = 0}^{L - 1} {h({Z_l})} \le \\ \frac{1}{2}\sum\limits_{l = 0}^{L - 1} {{\rm{lb}}} (2{\rm{\pi }}e({P_{s,l}} + {P_{N,l}})) - \frac{1}{2}\sum\limits_{l = 0}^{L - 1} {{\rm{lb}}} (2{\rm{\pi }}e{P_{n,l}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 0}^{L - 1} {\frac{1}{2}{\rm{lb}}} \left( {1 + \frac{{{P_{s,l}}}}{{{P_{n,l}}}}} \right) \end{array} $ | (5) |
根据仙侬原始论文(Shannon 1948) 与文献[1, 4, 7],等式成立即达到信道容量(最大互信息) 的条件,除Xk是相互独立的随机变量以外,Xk还必须是高斯分布.
特别是在各子信道的带宽分别为Bl,噪声均为功率谱密度为N0的独立白色高斯噪声时.各子信道可分别被其2Bl符号/s的离散无记忆(不相关,也就是独立) 样值序列所描述,则独立并联高斯信道的容量CK为
| $ {C_K} = \sum\limits_{k = 0}^{K - 1} {{B_k}} {\rm{lb}}\left( {1 + \frac{{{P_{s,k}}}}{{{N_0}{B_k}}}} \right) $ | (6) |
当各子信道均占据相同带宽B,系统各子信道的接收信号功率均为Ps/K时,该独立并联信道的容量CK为
| $ {C_K} = KB{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}BK}}} \right) $ | (7) |
显然只需证明OVXDM可以被分解成多个具有独立高斯噪声的并行子信道,则它就能形成独立并联高斯信道的传输系统.
1.2 白高斯噪声及其通过限频与限时信道的样值表示 1.2.1 定义众所周知,所谓白高斯噪声n(t)↔N(f) 是指除了其在频率域与时间域都是均值为零的高斯分布外,其频率域的功率谱密度是白色的,即
| $ {G_f}\left( f \right) = E\{ {\left| {N\left( f \right)} \right|^2}\} = {N_0}/2, - \infty < f < + \infty $ | (8) |
其时间域的功率谱密度也是白色的,即
| $ {G_t}\left( t \right) = E\{ {\left| {n\left( t \right)} \right|^2}\} = {N_0},{\rm{ }}0 \le t \le + \infty $ | (9) |
因为在频率域需要考虑负频率或者是调制后的上下边带,两边带形状对称且荷载相同的信息.而在物理可实现条件下,在时间域就没有对应的荷载相同信息的“负时间”或对称的“边带时间”.噪声在时间域与频率域的总功率(能量) 尽管都是无限大,但也必须相等.频率域有单边带宽与双边带宽之分,其单边带宽含义上的功率谱密度与时间域的功率谱密度在数值上应该相等(量纲不同),为方便起见不再分别表示.利用功率谱与相关函数之间的傅氏变换关系,容易求出白高斯噪声在时间域上的相关(协方差) 函数为
| $ E\left\{ {n\left( t \right)n\left( t \right)\prime } \right\} = \frac{{{N_0}}}{2}\delta \left( \tau \right),{\rm{ }}\tau = \left| {t - t\prime } \right| $ | (10) |
在频率域上的相关(协方差) 函数为
| $ E\left\{ {N\left( f \right)N\left( f \right)\prime } \right\} = {N_0}\delta \left(\mathit \Omega \right),{\rm{ }}\mathit {\Omega} = \left| {f - f\prime } \right| $ | (11) |
若信道传输函数的绝对带宽为B (单边),则白噪声经过这样的信道传输后,其输出噪声可以用其间隔为tB=1/2B的离散无记忆(不相关) 样值来描述:
| $ \sum\limits_l {{n_l}} {\rm{sinc}}[2{\rm{\pi }}B(t - l{t_B})] $ | (11) |
其中
| $ {\rm{sinc}}\;x = \frac{{{\rm{sin}}\;x}}{x},{\rm{ }}{t_B} = 1/2B $ | (12) |
| $ \begin{array}{l} {n_l} = \int_{ - \infty }^{ + \infty } {\sum\limits_l {n\left( t \right)} } {\rm{sinc}}[2{\rm{\pi }}B(t - l{t_B})],\\ \;\;\;\;\;\;l = 0, \pm 1, \pm 2 \cdots \pm \infty \end{array} $ | (13) |
{nl}为带宽为B的零均值独立高斯随机变量,它们的协方差为
| $ \begin{array}{l} E\{ {n_l}{n_{l\prime }}\} = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty E } \left\{ {n\left( t \right)n\left( {t\prime } \right)} \right\}{\rm{sinc}}[2{\rm{\pi }}B(t - \\ \;\;\;\;\;\;l{t_B})]{\rm{sinc}}[2{\rm{\pi }}B(t\prime - l\prime {t_B})]{\rm{d}}t{\rm{d}}t\prime = \frac{{{N_0}}}{2}{\delta _{l,l\prime }},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;l,l\prime \in \left\{ {0, \pm 1, \pm 2, \cdots , \pm \infty } \right\} \end{array} $ | (14) |
显然nl的分布为
| $ P({n_l}) = \frac{1}{{\sqrt {\pi {N_0}} }}{{\rm{e}}^{ - n_l^2/{N_0}}} $ | (15) |
若信道的冲击响应函数的绝对持续时间为T,则经过这样的信道传输后,其频率域输出噪声H(f)=0, ∀f∉[-B/2, +B/2), h(t))=0, ∀t∉[0, T) 可以用间隔为f=1/T的离散无记忆(不相关) 样值来描述:
| $ N\left( f \right) = \sum\limits_l {{N_l}} {\rm{sinc}}\left[ {{\rm{\pi }}T(f - l{f_T})} \right] $ | (16) |
| $ {N_l} = \int_{ - \infty }^{ + \infty } {\sum\limits_l {N\left( f \right)} } {\rm{sinc}}[{\rm{\pi }}T(f - l{f_T})]{\rm{d}}f $ | (17) |
Nl为持续时间为T的零均值独立高斯随机变量,其协方差为
| $ \begin{array}{l} \;\;\;\;\;E\{ {N_l}{N_{l\prime }}\} = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } E } \left\{ {N\left( f \right)N\left( {f\prime } \right)} \right\} \times \\ {\rm{sinc}}[{\rm{\pi }}T(f - l{f_T})]{\rm{sinc}}\{ {\rm{\pi }}T[f - \left( {l + k} \right){f_T}]\} {\rm{d}}f{\rm{d}}f\prime = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{N_0}{\delta _{l,l\prime }} \end{array} $ | (18) |
显然Nl的分布为
| $ P({N_l}) = \frac{1}{{\sqrt {{\rm{\pi }}{N_0}} }}{{\rm{e}}^{ - N_l^2/{N_0}}} $ |
图 2所示为利用重叠复用原理下的OVXDM系统模型,它是一个并行传输系统.由于移位间隔远小于复用波形的宽度,其输出波形会产生严重的重叠,其性能分析见文献[2-3, 5].下面将分析这种系统在AWGN信道中的重叠复用容量.
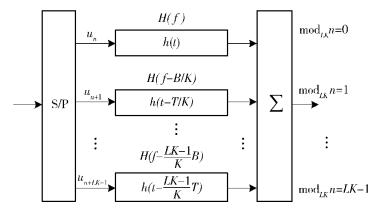
|
图 2 OVXDM系统模型 |
当信道传输函数H(f) 的单边带宽严格限定为B时,仙侬经典地仅利用信道时间域间隔为1/2B独立样值实施正交时分复用(OTDM, orthogonal time division multiplexing),得到了众所周知的AWGN信道容量C:
| $ C = B{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}B}}} \right) $ | (19) |
其中:Ps为信号的平均功率,N0为白高斯噪声的单边频谱密度.
OVFDM的做法完全不同,OVFDM虽然也充分利用信道在时间域的独立样值,但主要是利用信道在频率域的独立样值.由于此时对应信道冲击响应h(t)) 的持续时间T趋近于无穷,其频率域独立样点的间隔1/T必然趋近于零. OVFDM在频率域安排了K个独立样点,而且由于频率域独立样点的间隔1/T趋近于零,K无论取多大都属于欠采样.只要OVFDM的重叠重数K有限,其K个子信道的高斯噪声就是相互独立的.
众所周知,FTN也利用限带的信道传输函数H(f),但与仙侬的做法一样,FTN仍在时间域采样,FTN仅仅钻了滚降H(f) 绝对带宽宽于其奈奎斯特带宽的空子,得到点可怜的过采样增益,H(f) 滚降越小,FTN的增益越小.当H(f) 没有滚降,其绝对带宽等于奈奎斯特带宽时,FTN的增益将丧失殆尽.
下面就推导OVFDM的OV信道容量,与FTN截然不同,OVFDM主要在频率域采样,这里的唯一限制条件是信道传输函数H(f) 的单边带宽严格限定为B.至于复用波形是随机或非随机的,是随机或非随机编码或非编码序列,是随机或非随机编码矩阵等不做任何限制,关键是求出单位带宽单位时间的理论最大传信率C信道容量,理论只解决存在性,解决不了构造性.根据仙侬关于信道容量C的定义为
| $ C = \mathop {{\rm{max}}}\limits_{P\left( x \right)} = I\left( {X,Y} \right) $ | (20) |
在AWGN信道的OVFDM系统中,信道的输入为x(t),信道的输出为y(t)=x(t)+n(t),加性白高斯噪声为n(t),噪声时间域与频率域的谱密度均为N0.
由于信道传输函数H(f) 的单边带宽严格限定为B,在每秒时间内x(t)、y(t)、n(t) 可分别以其带宽为B的Nt=2B个时间域独立样点波形所描述,每个时间样点又有K个频率域独立样点,如前所述,K是不受限制的.这样,在单位时间内x(t)、y(t)、n(t) 分别由N=2KB个独立样点所描述,可分为两部分:第一部分为时间域样点序列:x(t)⇒XN=[x0, x1, …, x2B-1],y(t)⇒YN=[y0, y1, …, y2B-1], 对其中的每个时间域样点,又有K个独立的频率域样点序列:Xnt=[Xnt, 0, Xnt, 1, …, Xnt, K-1], Ynt=[Ynt, 0, Ynt, 1, …, Ynt, K-1], nt=0, 1, …, 2B-1.其中元素{Xnt, k}, {Ynt, k}均为频率域样点.先计算AWGN信道中每个时间域样点Xnt与Ynt(nt=0, 1, …, K-1) 之间的互信息为
| $ \begin{array}{l} \;\;\boldsymbol{I}({\boldsymbol{X}_{{n_t}}},{\boldsymbol{Y}_{{n_t}}}) = {\rm{ }}{\smallint _{{X_0}}} \cdots {\smallint _{{X_{K - 1}}}}{\smallint _{{Y_0}}} \cdots {\smallint _{{Y_{K - 1}}}}P({\boldsymbol{Y}_{{n_t}}}/{\boldsymbol{X}_{{n_t}}})P({\boldsymbol{X}_{{n_t}}}) \times \\ \;\;\;\;\;\;{\rm{lg}}\frac{{P({\boldsymbol{Y}_{{n_t}}}/{\boldsymbol{X}_{{n_t}}})}}{{P({\boldsymbol{Y}_{{n_t}}})}}{\rm{d}}{X_{{n_t},0}} \cdots {\rm{d}}{X_{{n_t},K - 1}}{\rm{d}}{Y_{{n_t},0}} \cdots {\rm{d}}{Y_{{n_t},K - 1}} = \\ \sum\limits_{k = 0}^{K - 1} {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty P } } ({Y_{{n_t},k}}/{X_{{n_t},k}})P({X_{{n_t},k}}){\rm{lg}}\frac{{P({Y_{{n_t},k}}/{X_{{n_t},k}})}}{{P({Y_{{n_t},k}})}}{\rm{d}}{X_{{n_t},k}}{\rm{d}}{Y_{{n_t},k}} \end{array} $ | (21) |
根据式(13) 可知:
| $ P({Y_{{n_t},k}}/{X_{{n_t},k}}) = \frac{1}{{\sqrt {{\rm{\pi }}{N_0}} }}{{\rm{e}}^{ - {{({Y_{{n_t}}} - {X_{{n_t}}})}^2}/{N_0}}} $ | (22) |
| $ P({Y_{{n_t},k}}) = \int_{ - \infty }^{ + \infty } P ({X_{{n_t},k}})P({Y_{{n_t},k}}/{X_{{n_t},k}}){\rm{d}}{X_{{n_t},k}} $ | (23) |
仙侬已经证明了当Xnt, k是统计独立的零均值高斯随机变量时,上述互信息最大,即
| $ P({\boldsymbol{X}_{{n_t}}}) = \prod\limits_{k = 0}^{K - 1} P ({X_{{n_t},k}}) = \frac{1}{{\sqrt {2{\rm{\pi }}{\sigma _x}} }}{{\rm{e}}^{ - {X_{{n_t}}}X_{{n_t}}^{\rm{T}}/2{\sigma ^2}}} $ | (24) |
这里σx2是每个Xnt, k的方差,即单个样点的平均功率,由于共有2KB个样点,必有
| $ {P_{\rm{s}}} = 2KB\sigma _x^2 $ | (25) |
这样,每个时间域Xnt与Ynt(nt=0, 1, …, K-1) 之间的最大互信息最终为
| $ \begin{array}{l} \mathop {{\rm{max}}}\limits_{P({X_{{n_t}}})} \boldsymbol{I}({\boldsymbol{X}_{{n_t}}},{\boldsymbol{Y}_{{n_t}}}) = \frac{1}{2}\sum\limits_{k = 0}^{K - 1} {{\rm{lb}}} \left( {1 + \frac{{2\sigma _x^2}}{{{N_0}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}K{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KB}}} \right) \end{array} $ | (26) |
OVFDM系统容量为每秒全部2B个时间域样点最大互信息之和,得
| $ \begin{array}{l} {\boldsymbol{C}_{{\rm{OVFDM}}}} = \sum\limits_{{n_t} = 0}^{2B - 1} {\mathop {{\rm{max}}}\limits_{P({X_{{n_t}}})} \boldsymbol{I}} ({\boldsymbol{X}_{{n_t}}},{\boldsymbol{Y}_{{n_t}}}) = B\sum\limits_{k = 0}^{K - 1} {{\rm{log}}} \left( {1 + \frac{{2\sigma _x^2}}{{{N_0}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;BK{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KB}}} \right) \end{array} $ | (27) |
如果仅仅利用时间域的独立样点,不利用频率域的独立样点,式(27) 将退化为众所周知的仙侬容量公式.
当K=1时,有
| $ \boldsymbol{C}_{{\rm{OVFDM}}}^\infty = \mathop {{\rm{lim}}}\limits_{K = 1} KB{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KB}}} \right) = \frac{{{P_{\rm{s}}}}}{{{N_0}}}{\rm{lb}}\;{\rm{e}} $ | (28) |
当信道冲击响应函数h(t)) 的持续时间严格限定为T时,经典方法是利用信道频率域间隔为1/T独立样值,实施正交频分复用OFDM. OVTDM的做法完全不同,OVTDM虽然也充分利用信道在频率域的独立样值,但主要是利用信道在时间域的独立样值.由于此时对应信道传输函数H(f) 的带宽B趋近于无穷,其时间域独立样点的间隔1/2B必然趋近于零. OVTDM在时间域安排了K个独立样点,而且由于时间域独立样点的间隔1/2B趋近于零,K无论取多大都属于欠采样.只要OVTDM的重叠重数K有限,其K个子信道的高斯噪声就是相互独立的.
下面推导OVTDM的重叠复用信道容量,这里的唯一限制条件是信道传输函数h(t)) 的持续时间严格限定为T.至于复用波形是随机或非随机的,是随机或非随机编码或非编码序列,是随机或非随机编码矩阵等不做任何限制,关键是求出单位带宽单位时间的理论最大传信率C-信道容量,理论只解决存在性,解决不了构造性.根据仙侬关于信道容量C的定义为
| $ \boldsymbol{C} = \mathop {{\rm{max}}}\limits_{P\left( x \right)} = \boldsymbol{I}\left( {\boldsymbol{X},\boldsymbol{Y}} \right) $ | (29) |
在AWGN信道的OVTDM系统中,信道的输入为x(t),信道的输出为y(t)=x(t)+n(t),加性白高斯噪声为n(t),噪声时间域与频率域的谱密度均为N0.
由于信道冲击响应函数h(t)) 的持续时间严格限定为T,在每赫兹带宽内x(t)、y(t)、n(t) 可分别以其宽度为T的Nf=T个频率域独立样点波形所描述,每个频率样点又有K个时间域独立样点,如前所述,K是不受限制的.这样,在单位带宽内x(t)、y(t)、n(t) 分别由N=KT个独立样点所描述,可分为两部分:第一部分为单位带宽内频率域样点序列:x(t)⇒XN=[x0, x1, …, xT-1],y(t)⇒YN=[y0, y1, …, yT-1],对其中的每个频率域样点,又有K个独立的时间域样点序列:Xnf=[Xnf, 0, Xnf, 1, …, Xnt, K-1],Ynf=[Ynf, 0, Ynf, 1, …, Ynt, K-1], nf=0, 1, 2…, T-1.其中元素{xnt, k}、{ynt, k}均为时间域样点.先计算AWGN信道中每个频率域样点Xnf与Ynf(nf=0, 1, …, K-1) 之间的互信息为
| $ \begin{array}{l} I({X_{{n_f}}},{Y_{{n_f}}}) = {\smallint _{{x_0}}} \cdots {\smallint _{{x_{K - 1}}}}{\smallint _{{y_0}}} \cdots {\smallint _{{y_{K - 1}}}}P({Y_{{n_f}}}/{X_{{n_f}}})P({X_{{n_t}}}) \times \\ \;\;\;\;\;\;{\rm{lg}}\;\frac{{P({Y_{{n_f}}}/{X_{{n_f}}})}}{{P({Y_{{n_f}}})}}{\rm{d}}{x_{{n_f},0}} \cdots {\rm{d}}{x_{{n_f},K - 1}}{\rm{d}}{y_{{n_f},0}} \cdots {\rm{d}}{y_{{n_f},K - 1}} = \\ \sum\limits_{k = 0}^{K - 1} {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty P } } ({y_{{n_f},k}}/{x_{{n_f},k}})P({x_{{n_f},k}}){\rm{lg}}\frac{{P({y_{{n_t},k}}/{x_{{n_f},k}})}}{{P({y_{{n_f},k}})}}{\rm{d}}{x_{{n_f},k}}{\rm{d}}{y_{{n_f},k}} \end{array} $ | (30) |
根据式(18) 可知:
| $ P({Y_{{n_f},k}}/{X_{{n_t},k}}) = \frac{1}{{\sqrt {{\rm{\pi }}{N_0}} }}{{\rm{e}}^{ - {{({Y_{{n_f}}} - {X_{{n_f}}})}^2}/{N_0}}} $ | (31) |
| $ P({Y_{{n_f},k}}) = \int_{ - \infty }^{ + \infty } P ({X_{{n_f},k}})P({Y_{{n_f},k}}/{X_{{n_f},k}}){\rm{d}}{X_{{n_f},k}} $ | (32) |
仙侬已经证明了当Xnf, k是统计独立的零均值高斯随机变量时,上述互信息最大,即
| $ P({\boldsymbol{X}_{{n_f}}}) = \prod\limits_{k = 0}^{K - 1} P ({X_{{n_f},k}}) = \frac{1}{{\sqrt {2{\rm{\pi }}{\sigma _x}} }}{{\rm{e}}^{ - {X_{{n_f}}}X_{{n_f}}^T/2{\sigma ^2}}} $ | (33) |
| $ P({\boldsymbol{X}_{{n_f}}}) = \prod\limits_{k = 0}^{K - 1} P ({x_{{n_f},k}}) = \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _x}}}{{\rm{e}}^{ - {X_{{n_f}}}X_{{n_f}}^T/2{\sigma ^2}}} $ | (34) |
这里σx2是每个Xnf, k的方差,即单个样点的平均功率,由于共有KT个样点,必有
| $ {P_{\rm{s}}} = KT\sigma _x^2 $ | (35) |
这样,每个频率域Xnf与Ynf(nf=0, 1, …, K-1) 之间的最大互信息最终为
| $ \mathop {{\rm{max}}}\limits_{P({X_{{n_f}}})} \boldsymbol{I}({\boldsymbol{X}_{{n_f}}},{\boldsymbol{Y}_{{n_f}}}) = {\rm{ }}\sum\limits_{k = 0}^{K - 1} {{\rm{lb}}} \left( {1 + \frac{{2\sigma _x^2}}{{{N_0}}}} \right) = K{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KT}}} \right) $ | (36) |
OVTDM系统容量为每赫兹全部T个频率域样点最大互信息之和,得
| $ \begin{array}{l} {\boldsymbol{C}_{{\rm{OVTDM}}}} = \sum\limits_{{n_f} = 0}^{T - 1} {\mathop {{\rm{max}}}\limits_{P({X_{{n_t}}})} } \boldsymbol{I}({\boldsymbol{X}_{{n_f}}},{\boldsymbol{Y}_{{n_f}}}) = B\sum\limits_{k = 0}^{K - 1} {{\rm{lb}}} \left( {1 + \frac{{2\sigma _x^2}}{{{N_0}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;K{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KT}}} \right) \end{array} $ | (37) |
可见OVTDM与OVFDM系统的容量在形式上是完全一致的,只是OVTDM系统容量全部以时间域参数表示,而OVTDM的系统容量则全部以与频率域对偶的时间域参数表示.噪声功率谱密度在时间域与频率域都为N0(数值相等,量纲不同).
3 重叠复用信道容量的物理意义 3.1 限时信道(OVTDM) 的重叠复用容量OVTDM要求系统冲击响应h(t)) 的持续时间T有限,与传统做法不同,它不在频率域反而在时间域独立采样.此时由于其独立样点间隔对应系统带宽B趋近于无穷而趋近于零,在时间域就可安排更多的独立样点.只要OVTDM各子信道的相对时间移位非零,它们子信道的高斯噪声就是相互独立的.加上OVTDM对其输入数据的独立高斯化处理,就得到了大容量的独立并联高斯信道-OVTDM.
基本条件与运算:
1) 系统冲击响应h(t)) 为实数,持续时间为T;
2) 系统接收信号总功率为Ps,K重重叠的OVTDM每支路接收信号功率为Ps, k,
3) 每一独立OVTDM支路在时间域的容量为
| $ {\boldsymbol{C}_{T,k}} = \frac{1}{2}{\rm{lb}}\left( {1 + \frac{{{P_{s,k}}}}{{{N_0}T}}} \right) $ | (38) |
OVTDM利用持续时间有限的冲击响应函数h(t)) 作移位重叠复用,由于移位噪声具有独立性,K重重叠的OVTDM系统相当于K元独立并联高斯信道,系统频谱效率相当于K个独立并行信道之和,容量达到
| $ {\boldsymbol{C}_{\rm{T}}} = \frac{1}{2}\sum\limits_{k = 0}^{K - 1} {{\rm{lb}}} \left( {1 + \frac{{{P_{s,k}}}}{{{N_0}T}}} \right) $ | (39) |
另外,不要忘了在频率域每赫兹还有T个独立样点以及当信道的冲击响应函数h(t)) 为实数时,还可以利用I和Q两信道的正交性传输. OVTDM的最终容量应比式(39) 再增加2T倍,达到
| $ {\boldsymbol{C}_{{\rm{OVTDM}}}} = T\sum\limits_{k = 0}^{K - 1} {K{\rm{lb}}} \left( {1 + \frac{{{P_{s,k}}}}{{{N_0}T}}} \right) $ | (40) |
特别是当各支路接收信号功率相等时,Ps, k=Ps/K:
| $ {\boldsymbol{C}_{{\rm{OVTDM}}}} = TK{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KT}}} \right) $ | (41) |
当K=1时,有
| $ \boldsymbol{C}_{{\rm{OVTDM}}}^\infty = \mathop {{\rm{lim}}}\limits_{K = 1} KT{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KT}}} \right) = \frac{{{P_{\rm{s}}}}}{{{N_0}}}{\rm{lb}}\;{\rm{e}} $ | (42) |
OVFDM要求系统传输函数H(f) 的单边带宽B有限,不在时间域反而在频率域独立采样.此时其独立样点间隔由于对应系统冲击响应的持续时间T趋近于无穷而趋近于零,在频率域就可安排更多的独立样点.只要OVFDM各子信道的相对频率移位非零,它们子信道的高斯噪声就是相互独立的.加上OVFDM对其输入数据的独立高斯化处理,得到了大容量的独立并联高斯信道-OVFDM.
基本条件与运算:
1) 系统传输函数H(f) 的单边带宽为B;
2) 系统接收信号总功率为Ps,K重重叠的OVFDM,每支路的接收信号功率为Ps, k,
3) 每一独立OVFDM支路在频率域的容量为
| $ {C_{F,k}} = \frac{1}{2}{\rm{lb}}\left( {1 + \frac{{{P_{{\rm{s}},k}}}}{{{N_0}B}}} \right) $ | (43) |
OVFDM利用单边带宽有限的传输函数为H(f) 作移位重叠复用,由于噪声具有独立性,K重重叠OVFDM系统相当于K元独立并联高斯信道,系统容量将达到
| $ C = \frac{1}{2}\sum\limits_{k = 0}^{K - 1} {{\rm{lb}}} \left( {1 + \frac{{{P_{s,k}}}}{{{N_0}B}}} \right) $ | (44) |
另外,不要忘了在时间域每秒还有2B个独立样点,因此OVFDM系统最终容量应比式(44) 再增大2B倍,达到
| $ C = B\sum\limits_{k = 0}^{K - 1} {K{\rm{lb}}} \left( {1 + \frac{{{P_{{\rm{s}},k}}}}{{{N_0}B}}} \right) $ | (45) |
特别是当各支路接收信号功率相等时,Ps, k=Ps/K:
| $ {\boldsymbol{C}_{{\rm{OVFDM}}}} = BK{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KT}}} \right) $ | (46) |
如果仅仅利用时间域的独立样点,不利用频率域的独立样点,式(46) 将退化为众所周知的仙侬容量.
当K=1时,有
| $ C_{{\rm{OVTDM}}}^\infty = \mathop {{\rm{lim}}}\limits_{K = 1} KB{\rm{lb}}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_0}KT}}} \right) = \frac{{{P_{\rm{s}}}}}{{{N_0}}}{\rm{lb}}\;{\rm{e}} $ | (47) |
可见,限频与限时信道的OV容量在形式上完全一致,只是限时信道的OV容量全部以时间域参数表示,而限频信道的OV容量则全部以与时间域对偶的频率域参数表示.噪声功率谱密度在时间域与频率域都为N0(数值相等,量纲不同).
3.3 系统频谱效率由于OVFDM是K元独立并联高斯信道,其系统容量、频谱效率、归一化信噪比均为各子信道之和,即
| $ \begin{array}{l} \eta = C/B,C = \sum\limits_{k = 0}^{K - 1} {{C_k},{\rm{ }}\eta } = \sum\limits_{k = 0}^{K - 1} {{\eta _k}} ,\\ \frac{{{E_{\rm{b}}}}}{{{N_0}}} = \sum\limits_{k = 0}^{K - 1} {\frac{{{E_{b,k}}}}{{{N_0}}}} ,{\rm{ }}k = 0,1, \cdots ,K - 1 \end{array} $ | (48) |
由式(45),在各个子信道中,有
| $ {2^{{\eta _k}}} = \left( {1 + \frac{{{P_{s,k}}}}{{{N_0}B}}} \right) = \left( {1 + \frac{{{E_{b,k}}{\eta _k}}}{{{N_0}}}} \right), \Rightarrow \frac{{{E_{b,k}}}}{{{N_0}}} = \frac{{{2^{{\eta _k} - 1}}}}{{{\eta _k}}} $ | (48) |
最终得
| $ {E_{\rm{b}}}/{N_0} = \sum\limits_{k = 0}^{K - 1} {{E_{b,k}}/{N_0}} = \sum\limits_{k = 0}^{K - 1} {\frac{{{2^{{\eta _k} - 1}}}}{{{\eta _k}}}} $ | (49) |
特别是:
1) 各独立并行支路都是二元(+1,-1) 数据输入子信道时,各子信道的频谱效率为ηk=1, ∀k=0, 1, 2, …K-1,有
| $ {E_{\rm{b}}}/{N_0} = \sum\limits_{k = 0}^{K - 1} {{E_{b,k}}/{N_0}} = \sum\limits_{k = 0}^{K - 1} {\frac{{{2^1} - 1}}{1}} = K,\eta = K $ | (50) |
这时的系统频谱效率与归一化门限信噪比都等于OVXDM的重叠重数K!
2) 各独立并行支路都是四元(+1, -1, +j, -j) 数据输入信道时,各子信道的频谱效率为ηk=2, ∀k=0, 1, 2, …K-1,有
| $ {E_{\rm{b}}}/{N_0} = \sum\limits_{k = 0}^{K - 1} {{E_{b,k}}/{N_0}} = \sum\limits_{k = 0}^{K - 1} {\frac{{{2^2} - 1}}{2}} = 1.5K,\eta = 2K $ | (51) |
这时系统的归一化门限信噪比等于1.5K, 系统频谱效率为2K.
图 3、图 4所示为各种理论界与OVXDM实际仿真结果比较.在频谱效率为2 kbit/symbol时,利用蒙特卡洛(Monte Carlo) 序列树图搜索算法,在Pb=10-5时仿真门限信噪比为42 dB.在频谱效率为200 bit/symbol时,利用滑动分组干扰抵消算法,在Pb=10-5时仿真门限信噪比为32 dB.由于采用了快速算法,性能有所损失,比OVXDM理论界恶化约6~8 dB.而对应的仙侬界分别为2 980 dB和579 dB,可见OVXDM的优越性!但是简单复用波形OVXDM的性能距其OV容量界还有相当距离,还有大量的特别是编码结构的重叠复用工作要做!
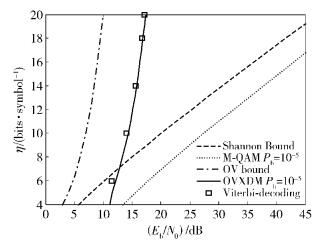
|
图 3 仙侬界、重叠复用容量界、OVXDM差错概率理论界与OVXDM仿真曲线比较1 |
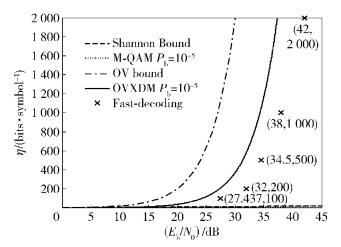
|
图 4 仙侬界、重叠复用容量界、OVXDM差错概率理论界与OVXDM仿真曲线比较2 |
笔者证明了在高斯白噪声干扰环境下,当信道传输函数H(f) 的单边带宽限定为B时,仅利用其时间域间隔为1/2B的独立样点处理是不够的,还可根据重叠复用原理,用频率域间隔为B/K独立样点的K重OVFDM,使系统容量达到KBlb
需要特别指出的是:仙侬是当之无愧的伟大科学家与先驱者,是他所创立的信息论一直在指导着通信事业的发展.但智者也会有些疏漏,甚至重大疏漏,例如:在限频信道中,仙侬只考虑了利用时间域独立样点去荷载数据,忽略了频率域独立样点也能荷载数据;仙侬还忽略了导出限时信道的容量.笔者虽然大幅度地提高了仙侬所导出的限频信道容量,但分析方法仍然是仙侬的基本方法.
致谢: 重叠复用原理与OVXDM是一项颠覆性的基础创新理论,与传统通信理论及人们的习惯性思维完全相悖.回想21年前我初步得出OVTDM差错概率的上界时,连我自己也不相信系统频谱效率会随信噪比线性增长,肯定我在什么地方搞错了.正是我的百余位研究生经过十多年反复不断地验证,证明了其正确性后,才最终使我坚定了信心,并发现了重叠复用原理.在这里,向辛勤劳作不断进取的研究生们表示衷心的感谢!另外对一贯支持本工作,不断提出指导性和修正完善建议的前辈和同事们表示衷心感谢!他们是我的已故恩师周炯槃院士、童志鹏院士、Prakis J G、Omura J K、已故吴佑寿院士、陈俊璧、杨千里、樊昌信、范平治、台湾陈晓华教授等.笔者特别感谢以深圳光启研究院季春霖副院长为首的OVXDM研发团队在OVXDM软硬件研究中的辛勤工作,OVXDM的频谱效率已被他们成功地在可实现信噪比条件下提升到千比特/符号的数量级.最后由衷地感谢北京邮电大学乔建永校长、任晓敏副校长等对本研究的重视,是他们给我创造了良好的研究环境,是他们组建了有多位教授分工合作的OVXDM后续研发梯队,使这项颠覆性创新基础理论研究能够持续不断地发展.还要感谢林鹏同学在本文发表过程中给予的帮助.| [1] | Thomas M Cover, Joy A Thomas. Elements of information theory[M].[S.l.]:John Wiley & Sons, 2006. |
| [2] | 李道本. 高频谱效率的波形编码理论--OVTDM及其应用[M]. 北京: 科学出版社, 2013. |
| [3] | Li Daoben. A novel high spectral efficiency waveform coding-OVFDM[J]. China Communications, 2015, 12(2): 61–73. doi: 10.1109/CC.2015.7084402 |
| [4] | Stephen G Wilson. Digital modulation and coding[M].[S.l.]:Prentice Hall Inc, 1996. |
| [5] | Li Daoben. A novel high spectral efficiency waveform coding-OVTDM, special issue on 5G wireless communication systems[J]. International Journal of Wireless Communications and Mobile Computing Systems, 2014(4-1): 11–26. |
| [6] | 李道本. 信号的统计检测与估计理论[M]. 2版. 北京: 科学出版社, 2005. |
| [7] | John G Proakis. Digital communications[M].[S.l.]:McGraw-Hill Communications Inc, 2001. |


