2. 中国民航大学 中国民航信息技术科研基地, 天津 300300
在综合管理X-软件系统测试数据生成中,针对遗传算法不能利用系统提供的信息,需要迭代多次才可找到测试数据,而蚁群算法在搜索初期信息素匮乏的情况下测试效率很低等问题,提出了基于混合遗传蚁群算法的测试数据自动生成方法,通过运行一定次数的遗传算法,产生优化解并作用于信息素的分布,再利用蚁群算法精确求解.在三角形程序和综合管理X-软件系统上的实验表明,该方法在保持性能不变的情况下,大幅降低了迭代次数和消耗时间,提升了测试效率.
2. Information Technology Research Base of CAAC, Civil Aviation University of China, Tianjin 300300, China
In integrated management X-software (IMX) system, genetic algorithm and ant colony algorithm have been used to generate the test data automatically. However, for genetic algorithm, it cannot use the information that provided by the system, thus it will iterate many times to generate the test data. For ant colony algorithm, there is little information pheromone on the path early, so it will take a long time to make it. Accordinly, a method based on hybrid genetic algorithm was proposed. First, execute the genetic algorithm for a few times. Second, use the optimization solution to make distribution for information pheromone. Finally, use ant colony algorithm to give the precision of the solution. Experiments on IMX and triangle program show that the hybrid algorithm has the characteristics of high efficiency, high quality, also it take fewer iterations to find the test data correctly and efficiently.
综合管理X-软件(IMX,integrated management X-software)系统是一套用于管理航空公司运行质量和安全审计的软件,系统开发周期非常短,且对运行质量和后期维护要求极高,研究IMX系统测试数据自动生成,实现其高效测试十分必要. 近年来,利用遗传算法(GA,genetic algorithm)、蚁群算法(ACO,ant colony optimization)等智能算法实现测试数据自动生成、提高测试效率的研究受到普遍关注,但GA自身无法利用系统中的反馈信息,且容易早熟收敛[1-2],往往需要迭代多次才可找到最优测试数据,而ACO又未能解决其在搜索初期由于信息素匮乏带来的求解效率慢等问题[3]. 笔者首先利用GA快速、全局收敛性等生成测试数据问题的优化解,再根据该优化解初始化信息素的分布,最后利用ACO求解精确解.
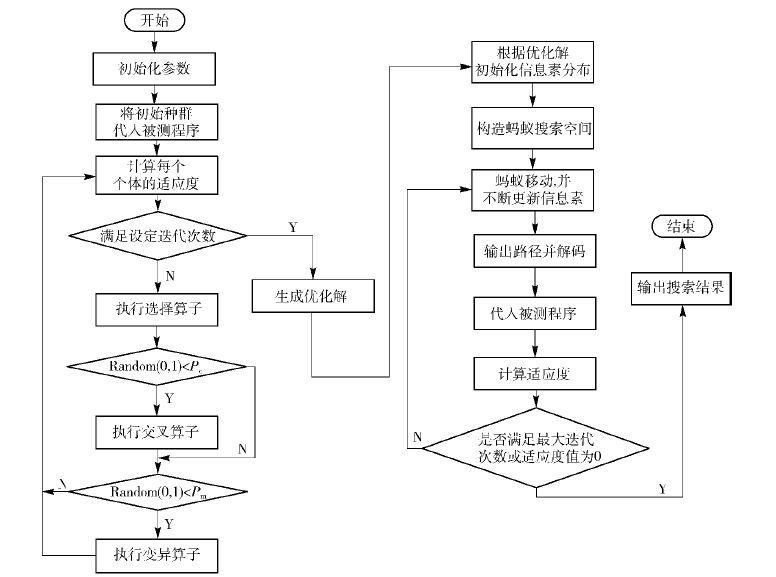
1 GA-ACO算法的提出在测试数据生成中,GA收敛性较好,但局部搜索能力较差,且由于无法利用系统中的反馈信息易导致大量的冗余迭代;而ACO则适应性好,局部搜索能力较强,但在搜索初期由于信息素的匮乏,求解效率低. 考虑到GA,ACO算法具有的互补性,可在ACO搜索前期,利用GA的全局收敛性实现对信息素的初始化分布,在GA搜索效率降低之前采用ACO进行精确求解. 笔者采用GA-ACO算法实现测试数据的自动生成,其基本思想为:利用GA的全局收敛性首先进行一定次数的迭代,搜索当前的优化解,并将此作为ACO初始信息素分布的依据,再利用ACO的正反馈机制进行精确求解. 两者的融合使算法优势互补,在求解效率上优于ACO,在求解精度上优于GA. 利用GA-ACO算法实现测试数据自动生成的流程图如图 1所示.
|
图 1 GA-ACO实现测试数据自动生成流程图 |
GA-ACO算法的时间复杂度主要取决于选择运算、交叉/变异操作和ACO操作,详述如下.
1) 选择运算:笔者采用轮盘赌选择策略,需与每一个体对应的角度值进行比较,其时间复杂度为O(i2),i为种群大小.
2) 交叉/变异操作:交叉、变异操作的时间复杂度为O(ni),其中n为个体染色体中基因位数.
3) ACO:ACO的整体复杂度为O(n4),n为节点的数量.
在最坏情况下,进化达到最大迭代次数为M,此时GA-ACO算法的时间复杂度为
OGA-ACO=max{O(Mi2),O(Mni),O(Mn4)}
与ACO算法相比,当n逐渐增大时,算法的复杂度也逐渐趋于O(n4),但由于GA-ACO算法避免了ACO算法初始信息素匮乏等问题,在实际应用中,其时间复杂度要远小于O(n4). 与GA算法相比,由于GA存在陷入局部最优的缺陷,会反复调度选择、交叉、变异等同一运算操作,大大增加了算法的时间复杂度,而GA-ACO算法会避免陷入局部最优,从而改善时间性能.
2 GA-ACO算法的实现 2.1 信息素的初始化在GA-ACO算法中,首先运行一定次数GA,生成问题的优化解,并对优化解对应的所有路径分支进行信息素的初始化,从而加大优化解路径上的信息素浓度,使ACO在搜索时能更有效地收敛于最优解.
优化解的确定依据为
| $S({{I}_{1}},{{I}_{2}})=\frac{N({{I}_{1}},{{I}_{2}})}{N({{I}_{2}})}~$ | (1) |
其中:I1为覆盖路径,I2为目标路径,N(I1,I2)为按节点序列匹配方法[4]寻找到的共同子路径的节点个数,N(I2)为目标路径的节点个数. 这里的覆盖路径是指测试数据所对应的路径,笔者选取的测试路径为目标路径. 覆盖路径与目标路径的相似度取值越大,表明测试数据质量越优.
初始化信息素的公式为
| $\tau ={{\tau }_{G}}+{{\tau }_{0}}$ | (2) |
其中:τG 为根据GA求解结果转换后的信息素的值[5],τ0为常量.
2.2 利用信息素寻找最优路径在GA-ACO算法中对参数采用二进制编码,假设共需N位二进制码,则蚂蚁的搜索空间大小也为N,其空间表示如图 2所示.

|
图 2 蚂蚁搜索空间 |
设蚂蚁的个数为n≤N,初始时每个节点的信息素浓度相等,记为τ0=C,C为常数. τ0取值不宜过大,为降低该参数对算法效率的影响,可利用C=n/Cnn求解,其中Cnn为被测程序中目标路径的距离.
每只蚂蚁在选择下一节点时,依据的移动规则计算公式为
| ${{P}_{ij}}^{k}\left( t \right)=\text{ }\left\{ \begin{align} & 0,其他 \\ & \frac{{{[{{\tau }_{ij}}(t)]}^{\alpha }}{{[{{\eta }_{ij}}(t)]}^{\beta }}}{\underset{s\in k\prime }{\mathop{\sum }}\,{{[{{\tau }_{is}}(t)]}^{\alpha }}{{[{{\eta }_{is}}(t)]}^{\beta }}},若\in k\prime ~ \\ \end{align} \right.$ | (3) |
其中:i、 j分别为起点和终点,k为第k只蚂蚁在进行搜索,τij(t)为在第t次迭代后由i到j的信息素强度,ηij为能见度,是i、 j两点之间距离的倒数,α、β分别为信息素和能见度的加权值,这里分别取值为1和2,k′为第k只蚂蚁尚未访问的节点集合. 根据式(3)即可求出尚未访问的节点被选择成为下一节点的概率,继续搜索蚂蚁空间,直到最后1个节点为止.
在求解过程中,蚂蚁按式(4)不断更新搜索过的每条边上的信息素为
| ${{\tau }_{ij}}(t)=\left( 1-\rho \right){{\tau }_{ij}}+\underset{k=1}{\overset{n}{\mathop{\sum }}}\,\Delta {{\tau }_{ij}}^{k}$ | (4) |
其中:ρ为信息素的蒸发率,在0和1之间取值. Δτijk计算公式为
| $\Delta {{\tau }_{ij}}^{k}=\left\{ \begin{align} & 0,其他 \\ & \frac{1}{{{C}_{k}}},若{{C}_{k}}包含e\left( i,j \right) \\ \end{align} \right.$ | (5) |
其中:Ck为第k只蚂蚁走完整条路径后所得总路径长度,e(i,j)为i到j这条边.
规范化后的适应度函数为分支距离与层接近度之和,计算公式为
| $F({{x}_{l}},t)=A({{x}_{l}},t)+(1-{{1.001}^{-B({{x}_{l}},t)}})~$ | (6) |
其中:F为适应度函数,A为层接近度,B为分支距离,xl为测试数据,l=1,2,…,L,L为基础数据的总个数,t为迭代的次数.
3 实验 3.1 实验数据和实验参数设置实验分别在三角形程序和IMX系统程序上展开,以验证笔者所提方法的有效性.
对于三角形被测程序选取了等边三角形作为目标路径. 在IMX系统中,笔者选取了审计模块中的审计状态变化过程,其中审计状态包括SCHEDULED、CONDUCTED、READY FOR CLOSE、CLOSED.
将算法的初始种群规模设为50,最大迭代次数为1 000,运行次数为20,交叉概率为Pc=0.8,变异概率为Pm=0.2,蚂蚁的个数设为10.
基于GA-ACO算法的测试数据自动生成,需要首先运行一定次数GA,迭代次数选择过小或过大均影响算法的收敛速度和求解效率[6]. 在实际应用中,应依据问题规模的大小来合理设置迭代的次数[5]. 笔者分别选取迭代次数为10、30、50进行了实验,图 3给出了不同迭代次数下所需GA迭代次数和GA-ACO生成测试数据所需代数的关系.

|
图 3 GA代数设定 |
图 3表明,将GA迭代次数选为30次为最佳.
3.2 实验结果与分析为了对比说明笔者算法的有效性,分别采用GA、ACO、GA-ACO和GA-ACO混合算法[7]这4种算法进行实验. GA-ACO混合算法是指在ACO搜索一定代数后,加入GA中的交叉思想,对搜索路径进行的交叉.
三角形中实验结果如表 1所示.
|
|
表 1 4种算法对比试验 |
由表 1可知,采用GA-ACO算法平均仅需迭代34.580次即可找到满足要求的数据,表现出很好的时间性能. 同时相比于传统的ACO,笔者所提方法增加了数据的多样性,且扩大了搜索空间.
对IMX系统程序,为验证笔者方法对输入参数不同取值范围的影响,分别取输入参数范围为(1,100),(1,400),(1,700),(1,1 000)进行实验. 实验结果如表 2~5所示.
|
|
表 2 取值范围(1,100)3种算法对比实验 |
|
|
表 3 取值范围(1,400)3种算法对比实验 |
|
|
表 4 取值范围(1,700)3种算法对比实验 |
|
|
表 5 取值范围(1,1 000)3种算法对比实验 |
从上述实验结果可以看出,1) 利用GA-ACO算法生成的测试数据能满足测试需求,可完全覆盖IMX系统中选取的被测程序,既能找到问题的最优解,又可保证测试数据的多样性;2) 随着参数取值范围的增加,GA-ACO算法均可在50代以内找到最优测试数据,有效避免了传统GA因无法利用系统中的反馈信息而导致的冗余迭代,同时解决传统ACO求解效率低下、消耗时间多等问题. 综上,GA-ACO算法在保持性能不变的前提下有效地提高了对IMX系统的测试效率,满足了IMX系统对自身测试的要求.
4 结束语在对IMX系统测试时,考虑到GA和ACO存在的互补性,笔者提出采用GA-ACO算法,即将GA运行一定次数后,产生问题的相关解,依此初始化信息素,再利用ACO求精确解. 在三角形程序和IMX系统上进行的实验表明,笔者方法可规避传统GA和传统ACO各自的缺陷,在更短的时间内通过更少的迭代次数搜索到符合要求的测试数据.
在利用GA实现测试数据自动生成时,编码方式不规范或选择不适当,会导致算法难以收敛于最优解,影响算法性能;在初期对初始种群选取时,采用轮盘赌选择策略,容易抛弃适应度低的个体,导致有可能产生最优解的个体也被丢弃. 因此,在利用GA实现测试数据自动生成时,如何选用合适的编码方式和选择策略仍需进一步的研究.
| [1] | 张岩, 巩敦卫. 基于稀有数据扑捉的路径覆盖测试数据进化生成方法[J]. 计算机学报 , 2013, 36 (12) :2429–2440. Zhang Yan, Gong Dunwei. Evolutionary generation of test data for paths coverage based on scarce data capturing[J]. Chinese Journal of Computers , 2013, 36 (12) :2429–2440. |
| [2] | 李剑, 牛少彰. 一种基于混合遗传算法的双多边多议题协商[J]. 北京邮电大学学报 , 2009, 32 (2) :1–4. Li Jian, Niu Shaozhang. A bilateral multi-issue negotiation based on hybrid genetic algorithm[J]. Journal of Beijing University of Posts and Telecommunications , 2009, 32 (2) :1–4. |
| [3] | Mao Chengying, Yu Xinxin, Chen Jifu, et al. Generating test data for structural testing based on ant colony optimization[C]//Quality Software (QSIC), 201212th International Conference on. IEEE, 2012: 98-101. |
| [4] | Xie Xiaoyuan, Xu Baowen, Shi Liang, et al. Genetic test case generation for path-oriented testing[J]. Journal of Software , 2009, 20 (12) :3117–3136. doi:10.3724/SP.J.1001.2009.00580 |
| [5] | 丁建立, 陈增强, 袁著祉. 遗传算法与蚂蚁算法的融合[J]. 计算机研究与发展 , 2003, 40 (9) :1351–1356. Ding Jianli, Chen Zengqiang, Yuan Zhezhi. On the combination of generation algorithm and ant algorithm[J]. Journal of Comouter Research and Development , 2003, 40 (9) :1351–1356. |
| [6] | 李剑, 景博. 自适应遗传算法在多边多议题协商中的应用[J]. 北京邮电大学学报 , 2008, 31 (6) :67–70. Li Jian, Jing Bo. Adaptive genetic algorithm and its application in multi-lateral multi-issue negotiation[J]. Journal of Beijing University of Posts and Telecommunications , 2008, 31 (6) :67–70. |
| [7] | 李克文, 张自鲁. 基于遗传-蚁群混合算法的软件测试数据自动生成方法[J]. 计算机工程与科学 , 2010, 32 (5) :51–53. Li Kewen, Zhang Zilu. A method for the automaitc test data generation based on the genetic-ant colony hybrid algorithm[J]. Computer Engineering and Science , 2010, 32 (5) :51–53. |


