2. 中国铁道科学研究院 电子计算技术研究所, 北京 100081
针对无线传感器网络中传感器节点的初始位置未知的问题,提出一种基于插值和规划算法的无线传感器网络三维节点定位算法.该算法利用锚节点坐标将节点所在空间曲面建立,并利用接收信号强度指示(RSSI)值和无线信号传播模型推导出所有可通信节点间相对距离.最后,利用0-1规划在空间曲面上选出满足距离约束且与未知节点数量相同的插值节点,从而估计出未知节点的空间位置.该算法设计简单,通信开销少.仿真结果表明,该算法具有较小的节点定位误差,并具有良好的稳定性和扩展性.
2. Institute of Computing Technology, China Academy of Railway Sciences, Beijing 100081, China
A new algorithm based on interpolation and 0-1 programming was presented for three-dimensional localization in wireless sensor networks. In this algorithm, the spatial interpolation surface of the nodes is established by the anchor nodes coordinates, and the distances of all the communication nodes are derived from the received signal strength indication (RSSI) and empirical radio propagation model. The 0-1 program is used to select the interpolation nodes with the same number of unknown nodes on the space surface. These selected interpolation nodes will meet the distance constraint so as to estimate the unknown node location. The algorithm is simple in design and the communication overhead is low. Simulation indicates that this algorithm has less error in the node localization. It also has good stability and extensibility.
未知节点定位是无线传感器网络研究中的重要技术之一,也是许多传感器网络研究开展的基础. 定位算法主要分为基于测距的定位算法和非测距定位算法两种. 基于测距的定位通过测量节点间的距离或角度信息,典型的距离测量技术包括利用到达时间(TOA,time of arrival)或到达时间差(TDOA,time difference of arrival)测距、利用到达角度(AOA,angle of arrival)测距以及利用接收信号强度指示(RSSI,received signal strength indicator)测距[1-2]. 非测距定位法则无需距离和角度信息,但得到的通常只是节点的粗定位.
在无线传感器网络的实际应用中,由于地形或者环境的限制,无线传感器往往在空间上分布,所以需要把定位研究扩展到三维空间中去. 吕等[3]提出一种基于球壳交集的APIS(approximate point in sphere)三维定位算法. 该算法不需要测距,但需要较高的节点密度来保证定位效果. Zhang 等[4]提出一种Landscape-3D空间定位算法. Shu等 [5]将体积测算引入APIT-3D定位的方法中,使得节点的定位精度有了一定的提升. 但当节点数量较多时,计算复杂度高. Wei等[6]对于三维节点定位使用了惯性权重的粒子群算法,取得了一定的效果. Yang等[7]将数字地形模型(DTM,digital terrain model)转换为三角网格,将每个传感器节点的网络与DTM的定位参考网格点对照来计算自己的地理位置.
提出一种基于部分节点空间位置已知(如通过GPS定位)的情况下,利用插值和规划算法的无线传感器网络三维节点定位算法.
1 算法模型 1.1 无向图模型用无向图模型代替对传感器网络的讨论. 设无向图G=(V,E),V为网络中传感器节点的集合. 若节点u,v∈V可以通信,则存在一条边e(u,v)∈E,E为边的集合. 图G中共有n个节点,其中有m个位置已知的锚节点. 对每一条边e(u,v)∈E都赋予一个权值r(u,v)∈R,在本算法中r为节点间的RSSI值.
设u,v间的距离为d(u,v),利用r(u,v)与d(u,v)之间的关系,可估算出可通信节点间的距离,进而用插值及规划算法进行定位.
1.2 利用RSSI值估算距离基于RSSI的测距技术利用无线电信号随距离增大而有规律地衰减的原理来测量节点间的距离的,其功率与距离之间的关系符合对数-常态分布模型[8].
设Pij为节点i接收到节点j发送信号后所测得的接收能量.
| ${{P}_{ij}}={{P}_{0}}-10nlg~({{d}_{ij}}/{{d}_{0}})$ | (1) |
其中:dij为i,j两节点间的真实距离,P0为相对于参考距离d0的接收能量,可由自由空间路径损耗公式计算,n为路径损耗指数,可取2~4. 考虑图G中的另一条边e(k,l),则有
| ${{P}_{kl}}={{P}_{0}}-10nlg~({{d}_{kl}}/{{d}_{0}})$ | (2) |
联立式(1),(2),取d0=1 m,得到
| $\frac{{{P}_{0}}-{{P}_{ij}}}{{{P}_{0}}-{{P}_{kl}}}=\frac{lg~{{d}_{ij}}}{lg~{{d}_{kl}}~}$ | (3) |
于是,就可得e(i,j)和e(k,l)两条边的距离的关系为
| ${{d}_{ij}}={{d}_{_{kl}}}{{~}^{\frac{{{P}_{ij}}-{{P}_{0}}}{{{P}_{kl}}-{{P}_{0}}}}}$ | (4) |
其中:Pij、Pkl可由测量得到;P0为已知量.
理想情况下,2点间距离与所接收到的信号强度成反比. 找出整个网络的全部RSSI值{r(i,j)}中的最小值为
| ${{r}_{min}}={{P}_{min}}=\underset{\left( i,j \right)\in E}{\mathop{mine}}\,r\left( i,j \right)$ | (5) |
将与Pmin对应的2点间最长距离记为dmax. 于是由式(4)可得
| ${{d}_{ij}}={{d}_{max}}^{\frac{{{P}_{ij}}-{{P}_{0}}}{{{P}_{min}}-{{P}_{0}}}}$ | (6) |
在实际中,由于节点随机分布,所以dmax趋近于节点的通信半径R. 本算法中近似地取dmax=R,代入式(6)中可得
| ${{d}_{ijEST}}={{R}^{\frac{{{P}_{ij}}-{{P}_{0}}}{{{P}_{min}}-{{P}_{0}}}~}}$ | (7) |
此外在实际环境中,无线信道受环境影响存在反射、折射、干扰等问题所产生的传播损耗. 为了模拟的真实性,在仿真部分对式(1)引入高斯噪声Xσ,Xσ表示均值为0、方差为σ的高斯随机变量.
1.3 空间插值算法实际应用中,传感器节点多被随机投放在三维空间内. 此时若提前对此处空间地面的地形地貌有所了解,那么对提高传感节点的定位精度将有极大帮助. 但之前的三维传感器定位过程的讨论中几乎都没有考虑到这一点. 笔者将利用已知位置的锚节点的三维坐标,通过基于三角形的线性插值方法得到一张与原始地形相近的一张插值曲面.
1.3.1 基于三角形的线性插值方法设在空间区域X×Y×ZR3(X,Y,Z分别为节点x,y,z坐标的取值范围)内有m个已知坐标的节点pi(xi,yi,zi)(i=1,2,…,m).
按以下步骤构造插值曲面近似代替曲面.
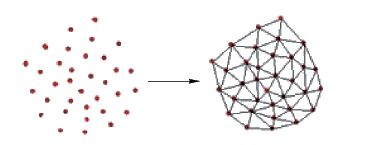
步骤1 使用最佳Delaunay三角形,可将节点所在区域由一张三角形拼接起来的网所覆盖,其中所有三角形的边都不能与另外的三角形相交. 而每一个三角形定义了一个覆盖该三角形内网格节点的面,如图 1所示.
|
图 1 Delaunay三角剖分 |
步骤2 选取一个待插值节点,找到此节点所属的三角形面. 由于三角形面由这个三角形的3个顶点数据确定,所以可用此数据求出三角面上任意节点的坐标.
设三角形3顶点的坐标分别为p1(x1,y1,z1),p2(x2,y2,z2),p3(x3,y3,z3),三角面上未知插的值节点坐标为p(x0,y0,z),x0,y0作为待插值节点位置是已知的. 由于p,p1,p2,p3四点共面,所以
| $\left| {\matrix{ {{x_0} - {x_1}} & {{y_0} - {y_1}} & {z - {z_1}} \cr {{x_0} - {x_2}} & {{y_0} - {y_2}} & {z - {z_2}} \cr {{x_0} - {x_3}} & {{y_0} - {y_3}} & {z - {z_3}} \cr } } \right| = 0$ |
解之可得待插值节点p的坐标p(x0,y0,z).
步骤3 对每一个待插值节点重复步骤2,可求出所有待插值节点坐标.
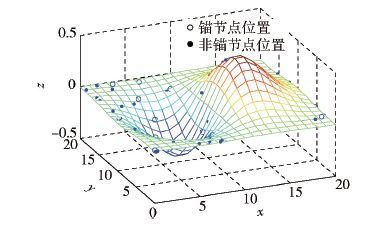
1.3.2 基于三角形线性插值方法的改进选择函数z=(0.2x-2)e-(0.2x-2)2-(0.2y-2)2,在一个20×20×2的区域随机生成100个随机点,从中再随机选择出20个节点作为锚节点,如图 2所示. 从图 2中可看出节点均匀地分布在三维曲面上.
|
图 2 所有节点在曲面上的分布情况 |
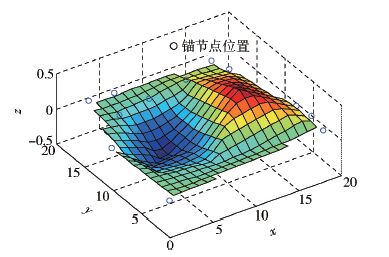
利用锚节点坐标已知的条件,使用基于三角形的线性插值方法可得插值曲面,如图 3所示.
|
图 3 插值曲面 |
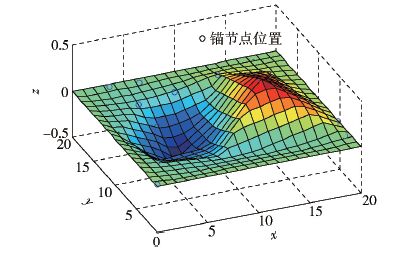
从图 3可以看出,对曲面插值运算时,4个边角都出现大片空白区域. 这是因为基于三角形的线性插值方法只能插值出空间节点网络的内部区域. 为了弥补这一缺陷,对此讨论区域首先补充4个边界点(0,0,z1),(20,0,z2),(20,20,z3),(0,20,z4)作为已知锚节点. 其次由连续曲面性质,分别选择与4个边界点水平距离最为相近的点的竖坐标作为该边界点的竖坐标值,这样插值效果有了明显提升. 如图 4所示,插值曲面完整覆盖了所有节点所在区域.
|
图 4 改进后插值曲面 |
设在所投节点区域内有m个锚节点(已知坐标的节点),n个非锚节点.
建立适当的三维坐标系,将所有节点放置于[0,a]×[0,b]×[c,d]的空间区域内. 在[0,a],[0,b]内等距插入点列
0=x1<x2<…<xk1=a
0=y1<y2<…<yk2=b
节点间距为λ,则
xk1=a+(k1-1)λ
yk2=b+(k2-1)λ
其中λ为分割细度. 这样就可在X×Y平面内插入k1×k2个节点,将这些插值节点称为伪节点. 令t=k1×k2,定位时伪节点的数量要求大于非锚节点数量,因此有t>n.
下边首先通过RSSI和式(7)计算所有非锚节点与锚节点间的估计距离矩阵Dij=(dijEST),其中i=1,2,…,n,j=1,2,…,m. 那么Dij中每一个行向量di代表其对应的非锚节点与所有锚节点的对应距离. 其次将伪节点以与其他节点相同的通信半径计算出伪节点与所有锚节点间的距离,得距离矩阵DljF=(dljF),其中l=1,2,…,t,j=1,2,…,m . 那么DljF中每一个行向量dlF代表其对应的伪节点与所有锚节点的相互距离. 最后,用0-1规划从所有t个dljF中选出n个构成矩阵DF,使之与Dij的距离‖DF-Dij‖2最小. 那么这n个伪节点就是非锚节点的估计位置. 设Xlj为0、1变量,具体0-1规划为
| $\eqalign{ & minJ = \mathop {\mathop \sum \limits^{{k_1} \times {k_2}} }\limits_{l = 1} {\mkern 1mu} \mathop {\mathop \sum \limits^m }\limits_{j = 1} {\mkern 1mu} {X_{lj}}{d_{lF}} - {d_j}{_2} \cr & s.t.{\rm{ }}\left. \matrix{ \mathop {\mathop \sum \limits^{{k_1} \times {k_2}} }\limits_{l = 1} {\mkern 1mu} {X_{lj}} = 1 \hfill \cr \mathop {\mathop \sum \limits^m }\limits_{j = 1} {\mkern 1mu} {X_{lj}} \le 1 \hfill \cr} \right\} \cr} $ | (8) |
为了求解此规划问题给出如下的定义.
定义 称原0-1规划为IP,而取消其相应整数约束的线性规划为LP.
因为整数规划问题的最优目标值不会优于线性规划问题的最优值,所以采用分支定界法来求解此问题. 具体求解步骤如下.
步骤1 求解LP,如果LP无解,则停止计算,这时IP也无解.
步骤2 如果求得LP的最优解且符合整数条件,则它就是IP的最优解,停止计算. 否则,转步骤3.
步骤3 在LP的解中任选一个不符合整数条件的变量xj,把原问题分解成2支,各支分别增加一个约束条件:1) xj=0;2) xj=1.
不考虑整数条件,分别称为问题LP1和LP2. 解LP1和LP2.
步骤4 在现有的,且还没有分解出分支问题的各可行解问题中,选目标函数值为最优的问题. 重新称这问题为LP,回到步骤2,重复进行.
下面对此算法的复杂度进行分析. 将此算法中所有变量的个数记为w,易知w=t×n. 对此问题进行一次线性规划计算的复杂度上界为O(w2),从算法中可知为了得到最终结果,最坏情形下需要做的分支次数也不超过w2次. 综合分析得出,此算法的复杂度为O(w3). 因此,给出的算法是多项式算法,本算法是有效的.
2 实验结果 2.1 定位误差实验在Matlab环境下进行. 设传感器节点的通信半径R=50,实验首先在4R×4R的感知区域内均匀分存100个传感器节点,节点间的RSSI值使用经验的无线信号传播模型进行模拟[8]为
Pij=P0-10nlg (dij/d0)+Xσ
在式中加入Xσ表示均值为0、方差为σ的高斯随机变量. 在实际环境中,无线信道受环境影响会产生不同的传播损耗,为模拟真实性引入高斯噪声Xσ. 实验中取P0=-30 dBm,d0=1 m,n=3,σ=2.
将未知节点i的真实坐标记为 preali=(xreali,yreali,zreali),估算得到的坐标表示为pesti=(xesti,yesti,zesti),那么
| $E=\frac{1}{n}\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\|{{p}_{est}}^{i}-{{p}_{real}}^{i}{{\|}_{2}}$ | (9) |
其中E为节点的平均定位误差. 此外,一般用E与节点通信半径R的比值来表示定位精度.
实验随机生成100个网络,平均网络连通度为15. 将20个锚节点与80个非锚节点随机散布在区域内(出于成本的考虑,锚节点数量一般不会超过总节点数量的20%),曲面为z=(0.2x-2)e-(0.2x-2)2-(0.2y-2)2. 在100次定位中的平均定位误差为16.5%,对比同类问题的处理结果[6],提出的方法定位精度更高.
2.2 定位精度分析 2.2.1 锚节点个数及通信半径对节点定位的影响实验在Matlab环境下进行,在200×200的感知区域内随机均匀分存100个传感器节点.
1) 设通信半径R=50,分割细度λ=1.
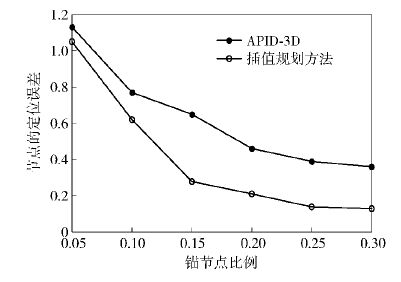
图 5表明锚节点个数对节点定位精度的影响.
|
图 5 锚节点比例对定位误差的影响 |
从图 5可看出,随着锚节点比例的增加,定位误差不断缩小. 与APIT-3D定位法比较提出的方法定位误差更小. 在2.2.2节中将讨论到随着分割细度的缩小,误差在一定程度上还可进一步缩小.
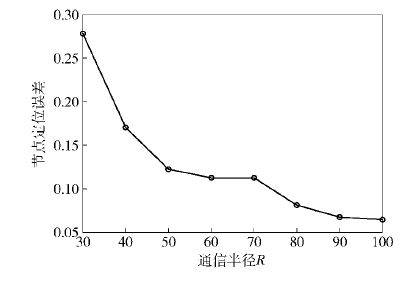
2) 设锚节点个数为20,图 6表明不同的通信半径对节点定位精度的影响.
|
图 6 不同通信半径R下的节点定位精度 |
从图 6可以看出,随着通信半径的增加,节点的定位精度不断缩小. 综合图 5、图 6的仿真结果可以看出,提出的算法对于不同节点数量和有不同的节点通信半径的无线传感器网络都有较好的定位精度和良好的可扩展性.
2.2.2 分割细度对节点定位精度的影响在200×200的区域内对同一组节点,用不同细度进行分割,分别讨论其定位精度,如表 1所示.
|
|
表 1 分割细度对节点定位精度的影响 |
通过表 1可以看出,随着分割细度λ的减小,定位误差不断减小,使得在定位非锚节点时的误差可控. 但减小分割细度,相应的也会增加伪节点的数量,从而使得计算的复杂程度提高. 且还发现,当伪节点的数量增加到一定程度的时候,定位误差很难再缩小,这主要是由于在利用锚节点坐标进行曲面插值及RSSI测距的过程中产生的误差不能由增加伪节点的数量来弥补.
3 结束语提出一种在部分节点空间位置已知(如通过GPS定位)的情况下,基于插值和规划算法的无线传感器网络三维节点定位算法. 该算法充分考虑了地形对传感器节点定位的辅助作用,且设计简单,节点间只需广播一次,通信开销少. 另外,对比可知提出的方法定位误差更小,且定位误差可通过插值节点的密度在一定范围内实现可控. 所以此方法更适用于实际.
对于此算法,考虑到实际中影响RSSI值的因素较多,下一步将考虑如何利用算法对可通信节点间距离进行校正,提高测距精度,从而提高定位算法的精度. 且还考虑利用锚节点建立插值曲面时可尝试使用不同的插值方法,进一步降低计算复杂程度和提高节点定位精度.
| [1] | Awad A, Frunzke T, Dressler F. Adaptive distance estimation and localization in WSN using RSSI measures[C]//10th Euromicro Conference on Digital System Design Architectures, Methods and Tools. Lubeck: IEEE Computer Society, 2007: 471-478. |
| [2] | Patwari N, Alfred O. Using proximity and quantized RSS for sensor localization in wireless networks[C]//Proceedings of the Second ACM International Workshop on Wireless Sensor Networks and Applications. New York: Association for Computing Machinery, 2003: 20-29. |
| [3] | 吕良彬, 曹阳, 高洵, 等. 基于球壳交集的传感器网络三维定位算法[J]. 北京邮电大学学报 , 2006, 29 (S1) :48–51. Lv Liangbin, Cao Yang, Gao Xun, et al. Three dimensional localization schemes based on sphere intersections in wireless sensor network[J]. Journal of Beijing University of Posts and Telecommunications , 2006, 29 (S1) :48–51. |
| [4] | Zhang Liqiang, Zhou Xiaobo, Cheng Qiang. Landscape-3D: a robust localization scheme for sensor networks over complex 3D terrains[C]//Proceedings of the 31st Annual IEEE Conference on Local Computer Networks. Washington D C,[S.l.]: IEEE Press, 2006: 239-246. |
| [5] | Shu Jian, Yan Chuan, Liu Linlan. Improved three-dimensional localization algorithm based on volume-test scan for wireless sensor networks[J]. The Journal of China Universities of Posts and Telecommunications , 2012, 19 (2) :1–6. doi:10.1016/S1005-8885(11)60238-0 |
| [6] | Wei Nuo, Guo Qiang, Shu Minglei, et al. Three-dimensional localization algorithm of wireless sensor networks base on particle swarm optimization[J]. The Journal of China Universities of Posts and Telecommunications , 2012, 19 (2) :7–12. |
| [7] | Yang Yang, Jin Miao, Wu Hongyi. 3D surface localization with terrain model[C]//Proc of the 33rd Annual IEEE Int Conf on Computer Communications. Toronto: IEEE, 2014: 46-54. |
| [8] | Rappaport T S. Wireless communications: principles and practice[M]. Englewood Cliffs: Prentice-Hall , 2002 : 107 -109. |


