已有的位置隐私保护下的连续最近邻查询往往采用snapshot方式进行,导致较高的中央处理器开销.为此,研究了基于位置隐私的连续最近邻查询,提出了基于重用技术的位置隐私保护的连续最近邻查询算法.该算法利用相邻时刻查询结果集的相似性来减少计算成本,从而实现答案集的快速更新,可大大加快系统响应时间.实验结果表明了该算法的有效性.
Enjoying the location-based service (LBS), the mobile subscribers may threaten the disclosure of location privacy. To protect location privacy, an effective method for location privacy preserving was proposed to cloak the user's exact coordinates into a spatial region and turn the location-based query into region-based query. Existing continuous nearest-neighbor query algorithms with privacy-aware are based on snapshot, which incur higher central processing unit (CPU) cost. The location privacy-based continuous nearest-neighbor query was studied and an algorithm named reusing-based location privacy-preserving continuous nearest-neighbor query (RLPCNN) which is based on reusing technique query updating was proposed. The algorithm can reduce the cost of computation by using the similarity between the two adjacent time and make the answer set updated quickly, which can quicken the response time markedly. The experiments show that the algorithm is effective and efficient.
在基于位置的服务中,移动用户必须向服务方提供地理位置,这势必造成移动用户位置隐私的泄露,其安全受到威胁. 位置隐私保护中一个重要的方法是将移动用户的精确位置匿名成一个空间区域[1]. 请求服务时,移动用户将该区域提交给位置数据库服务器,服务器根据移动用户提交的区域进行查询并将结果返回给移动用户. K-匿名模型最早由Gruteser等[1]引入位置隐私保护领域. Tao等[2]首次提出一种有效处理连续最近邻查询算法,以增量方式获取查询点的最近邻点. Hu等[3-7]相继提出了位置隐私保护下的最近邻查询算法.
位置服务的使用者往往处于移动状态,其位置的变化导致查询结果的变化. 现在算法多以snapshot方式处理查询,对连续最近邻查询要求每时每刻都重新计算答案集,延缓了响应时间,加剧了系统的负担. 笔者提出了基于重用技术的位置隐私保护的连续最近邻查询算法(RLPCNN,reusing-based location privacy-preserving continuous nearest-neighbor query). 该算法在不失查询准确性的条件下,充分利用连续查询相邻时刻匿名区域的相似性来实现答案集的快速更新,减少计算成本,加快响应时间,很好地解决连续最近邻查询处理问题.
1 位置隐私查询匿名器采用quad-tree动态管理移动用户地理位置,整个空间被划分成面积相等的单元区域,quad-tree每层管理大小不一致的空间区域,叶子节点管理细粒度的子空间,根节点管理粗粒度的整个空间. 矩形空间为Rect(L,B,R,T),(L,B)为矩形的左下角点的坐标,(R,T)为矩形的右上角点的坐标.
1.1 相异度函数相异度函数是描述不同时刻匿名区域相似程度的度量函数,在不同时刻i,j,系统为移动用户生成的匿名区域为Bcl(mti),Bcl(mtj),令vk(1≤k≤4)为匿名区域的顶点,ek(1≤k≤4)为边界,令Bi=Bcl(mti),Bj=B(mtj).
定义1 不同时刻的相异度函数定义为
| $\eqalign{ & D\left( {{B_i},{B_j}} \right) = \cr & \left\{ \matrix{ 0,{B_i} = {B_j} \hfill \cr 1/4,\exists {e_k} \in \{ {B_i}{e_k},{B_j}{e_k}\} \left( {1 \le k \le 4} \right),{e_k} = {B_i} \cap {B_j} \hfill \cr 1/2,\exists {e_k} \in \{ {B_i}{v_k},{B_j}{v_k}\} \left( {1 \le k \le 4} \right),{v_k} = {B_i} \cap {B_j} \hfill \cr 1,{\rm{其他}} \hfill \cr} \right. \cr} $ |
如图 1所示,计算t0、t1时刻的匿名相异度D(B0,B1)=1/2,可重用t0时刻对于顶点v1的最近邻点. 计算t2、t3时刻匿名相异度D(B2,B3)=1/4,可重用相交区域最下面的2个顶点,即t2时刻e1上面的扩展边. t4、t5时刻形成的匿名区域完全重合,D(B4,B5)=0,故在t5时刻可完全重用t4时刻的结果集.
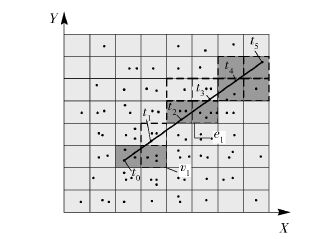
|
图 1 移动用户在不同时刻产生的匿名区域 |
移动用户提出连续最近邻查询,相邻时刻得到的查询集存在一定的相似性,RLPCNN算法的思想就是利用这些相似性来减少计算成本. Casper算法[3]采用自底向上搜索quad-tree的方式来为移动用户搜查满足匿名要求的矩形区域,在quad-tree的底层,节点是一些大小相等的矩形区域. 移动用户成功匿名后将得到一个匿名区域,位置数据库服务器接收该匿名区域进行查询处理得到候选答案集. 对于基于区域的最近邻查询,Rbulk算法[3]能一次性获得匿名区域的所有最近邻点,提出了Rbulk的变种ARbulk算法,一方面获得匿名区域的所有最近邻点,另一方面存储各个时刻的候选答案集.
ARbulk算法中3个Set变量preCA、preNT、preED分别用来存储初始时刻的答案集、匿名区域4个顶点的最近邻(ti. NN)集和匿名区域4条边上的扩展距离集(edij). RLPCNN算法先调用ARbulk得到上一时刻的匿名区域最近邻目标对象点的答案集,通过计算当前匿名区域与上一时刻匿名区域的相异度来决定重用答案集的力度. RLPCNN算法的表述如下.
算法1 RLPCNN
Input: Region(Cid,L,B,R,T) //输入匿名区域
Output: CAS //得到候选答案集
1 ARbulk(C′id) //Cid为上一时刻的匿名区域
2 flag=D(preRegion,Region) //计算相邻时刻匿名区域的相似性
3 if flag=0
4 return CAS←preCA //完全重用上一时刻答案集
5 else if flag=1/4
6 edij←preED //重用匿名区域上的扩展边集
7 computer the rest edij and form the expand region
8 return CAS←All target objects inside the new region //扫描得到答案集
9 else if flag=1/2
10 ti. NN←preNT //重用匿名区域顶点的最近邻目标对象集
11 computer the rest ti. NN,then get the edij of each edge and form the expand region
12 return CAS←All target objects inside the new region
13 else AlterativeRbulk(Cid) //重新计算得到答案集
14 return CAS←preCA
1.3 RLPCNN时间性能分析令Nt为目标对象的数目,Tquery为查询时间,Rcloak为匿名区域,Rclock.h和Rclock.w分别为匿名区域的长度和宽度,h和w为整个空间区域的长度和宽度,α、β为单元格的长度和宽度,M、N为系统区域逻辑行和列. 假定目标对象服从均匀分布,可得查询处理时间为
| $\begin{align} & {{T}_{query}}={{a}_{0}}MN+{{a}_{1}}\frac{{{R}_{clock}}.h\times {{R}_{clock}}.w}{\alpha \beta }+ \\ & {{a}_{2}}\frac{{{R}_{clock}}.h\times {{R}_{clock}}.w}{hw}{{N}_{t}} \\ \end{align}$ |
其中a0、a1、a2为常系数.
在给定系统逻辑空间后,查询处理时间正比于目标对象点的数目,即可得查询处理时间复杂度为O(kNt).
1.4 RLPCNN有效性证明相比snapshot方式的连续最近邻查询,笔者采用重用技术进行连续最近邻查询的答案集的更新,大大加快了查询的速度.
定理1 给定匿名区域Rcloak,用户u位于Rcloak的任何位置,则RLPCNN返回的候选答案集一定包含u的最近邻目标对象.
定理2 给定匿名区域Rcloak,用户u可位于Rcloak任何位置,RLPCNN得到的扩展区域是最小的,即得到的候选答案集是最小的.
定理1和定理2证明略.
由定理1和定理2可知,RLPCNN在降低查询处理成本的情况下,能保证移动用户最近邻点一定在候选答案中,验证了RLPCNN的准确性;同时又能保证所得的候选答案集最小,显示了RLPCNN算法的优越性.
2 实验及分析使用C++语言实现上述算法,实验环境为Intel Pentium(R) Dual-Core E5700 3.00 GHz,2 G RAM,Windows XP的PC. 实验中所有的移动用户是由基于网络的移动对象生成器[8]生成,输入端为美国明尼苏达州亨内平县(Hennepin County,MN,USA)道路地图. 输出为一系列位于道路上的移动用户. 移动用户在该地图上随机地移动,在某个固定的区域内,不同时刻移动用户的数目很大程度上是不同的.
该实验着重在不同数据规模、不同K值范围等情形下,RLPCNN算法与Rbulk算法[3]的平均中央处理器处理时间(CPT,central processing unit processing time)性能对比和在不同参数下RLPCNN算法的性能变化. 实验中目标对象点的分布有高斯(Gaussian)分布和均匀(Uniform)分布2种,实验中的算法名称表示如下.
U-Rbulk算法为Uniform分布下Rbulk算法,U-RLPCNN算法为Uniform分布下RLPCNN算法,G-Rbulk算法为Gaussian分布下Rbulk算法,G-RLPCNN算法为Gaussian分布下RLPCNN算法.
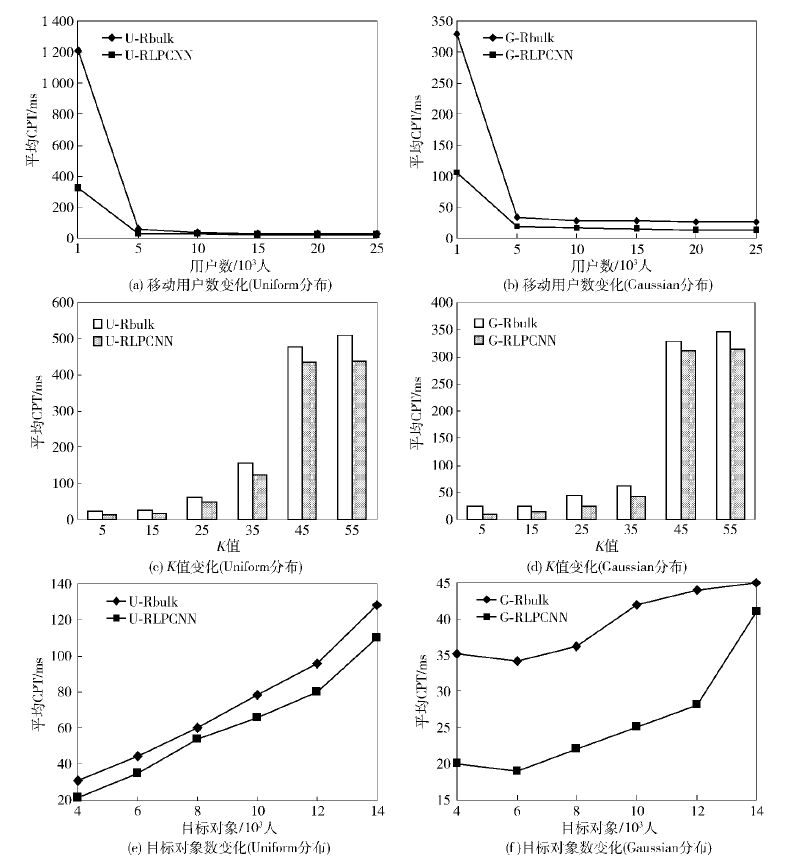
2.1 移动用户数、K值和目标对象数对算法效率的影响当移动用户数较少时,匿名算法为了满足移动用户的隐私要求形成一个较大的匿名区域,在目标对象数一定时形成扩展区域随之增大,导致较高的计算成本;当移动用户数增大时,匿名区域会变小,随之而来的扩展空间减小,导致较低的计算成本. 图 2(a)和图 2(b)显示了移动用户数发生变化时,RLPCNN算法与Rbulk算法的性能对比. 当移动用户数目较少时,RLPCNN算法消耗时间较少,性能较佳;当移动用户数目增大时,RLPCNN算法时间性能趋同Rbulk算法. 在Gaussian分布情况下,RLPCNN算法也表现出相似的性能优势. 因为RLPCNN算法利用了相邻匿名区域的相似性,可快速更新答案集,时间成本小于Rbulk算法. Guassian分布使目标对象较集中,RLPCNN在此情况下表现出的性能优势更明显.
当K值变化时,RLPCNN算法也显示出较佳的性能,如图 2(c)和图 2(d)所示. 随着K值变大,移动用户的隐私要求变高,匿名算法为满足移动用户不断变高的隐私要求产生的匿名区域将变大,造成的扩展空间随之增大,计算成本增高. RLPCNN利用了相邻时刻匿名区域的相似性,可快速更新答案集,降低计算成本.
|
图 2 移动用户数、K值和目标对象数对算法效率的影响 |
当目标对象数发生变化时,RLPCNN算法同样表现出较好的时间优势. 如图 2(e)和图 2(f),在移动用户数和K值不变的情况下,目标对象数增大时,2种算法消耗时间逐步增大,这是由于目标对象的增加导致扫描时间的增加,导致时间成本增加. 但RLPCNN算法由于保留了前一时刻的答案集,并利用相似性快速更新答案集,降低了时间成本.
2.2 数据分布对候选答案集和结果集的影响候选答案集是指扩展区域内所有目标对象的集合. 移动用户请求最近邻查询时,候选答案集区域越小,体现算法性能越好. 图 3显示了在不同数据分布的情形下,RLPCNN算法的性能. 显而易见,在Gaussian分布下,RLPCNN算法性能更佳. 随着移动用户数增加,满足用户隐私要求的匿名区域越来越小,形成的扩展区域随之减小,因此形成的候选答案集也减小. 在Gaussian分布的情况下,目标对象形成的扩展区域较小,故候选答案集较少. 当移动用户数目和目标对象数目不变时,随着K值变大,移动用户的隐私要求变高,形成的匿名区域和扩展区域变大,故候选答案集变小. 当移动用户数目和K值不变时,目标对象增加,促使落在扩展区域中目标对象数目的增加,故候选答案集变大.
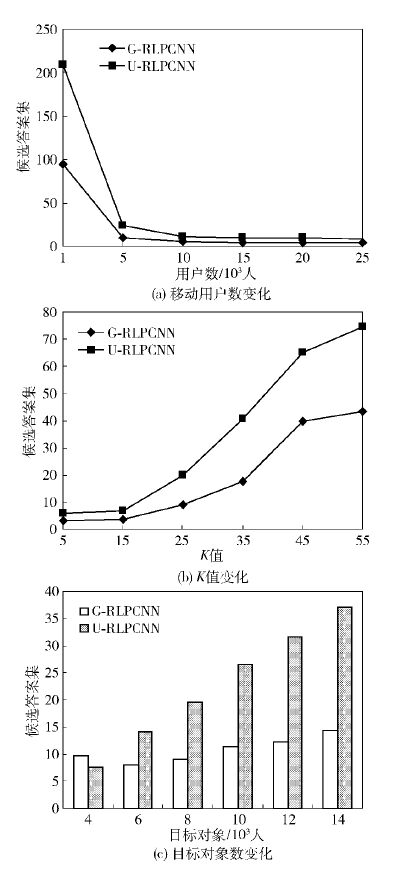
|
图 3 不同分布对候选答案集的影响 |
最终结果集是指位置数据库服务器将候选答案集返回给匿名器后,匿名器经过精细化处理,最后将最终结果集返回给用户. 最终结果集过大会给传输带来负担,且导致响应时间过长. 最终结果集越小,越能减少用户请求服务的响应时间. RLPCNN算法在2种不同分布下表现出的性能有所差异,在同等条件下,RLPCNN算法Gaussian分布产生的最终结果集要少于Uniform分布,如图 4所示. 随着移动用户数的增加,匿名算法产生的匿名区域变小,随之产生的扩展区域变小,导致的候选答案集变小,结果集也变小. 随着K值变大,匿名算法产生的匿名区域变大,导致的最终结果集变大. 随着目标对象数目的增加,在匿名区域不变时,落在扩展区域中目标对象的数目将增加,导致的最终结果集增加. 当目标对象服从Gaussian分布时,目标对象分布更集中,导致相邻时刻产生的候选答案集有很大的交集,故产生的最终结果集少于Uniform分布的情况.
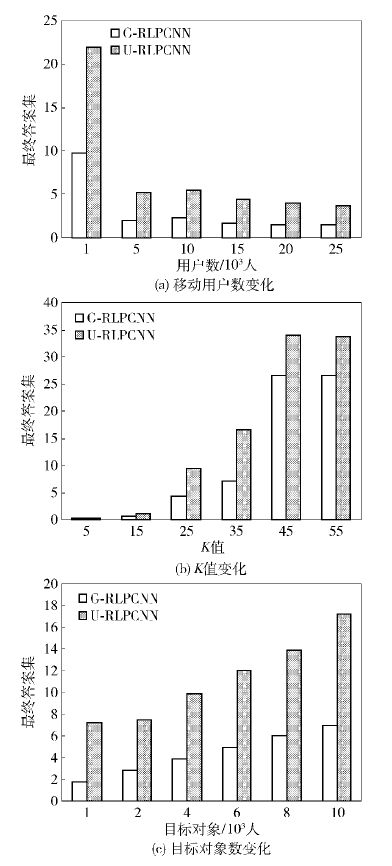
|
图 4 不同分布对最终答案集的影响 |
探讨了位置隐私保护中连续最近邻查询的问题,提出RLPCNN算法能有效处理位置隐私保护中连续最近邻查询. 主要思想为相邻查询时刻定义了相异度函数,通过计算相邻时刻产生的匿名区域的相似程度来决定如何重用上一时刻结果集,从而实现快速更新答案集,减少计算成本. 最后通过实验验证,RLPCNN算法表现出优越的性能.
| [1] | Gruteser M, Grunwald D. Anonymous usage of location-based services through spatial and temporal cloaking[C]//Proceedings of the International Conference on Mobile Systems, Application, and Services (MobiSys'03). Scan Francisco:[s.n.], 2003: 163-168. |
| [2] | Tao Yufei, Papadias D, Shen Qiongmao. Continuous nearest neighbor search[C]//VLDB Conference. Hongkong:[s.n.], 2002: 287-298. |
| [3] | Hu Haibo, Lee D L. Range nearest-neighbor query[J]. IEEE Trans Knowledge and Date Eng , 2006, 18 (1) :78–91. doi:10.1109/TKDE.2006.15 |
| [4] | Mokbel M F, Chow C, Aref W G. The new casper: query processing for location services without compromising privacy[C]//Proceedings of the 33rd International Conference on Very Large Data Bases (VLDB'06). Seoul:[s.n.], 2006: 736-774. |
| [5] | Ghinita G, Kalnis P, Skiadopoulos S. PRIVE: anonymous location-based queries in distributed mobile systems[C]//Proceedings of International Conference on World Wide Web (WWW'07) Banff. Alberta:[s.n.], 2007: 371-380. |
| [6] | Cheng Reynold, Chen Jinchuan, Mokbel M F, et al. Probabilistic verifiers: ebaluating constrained nearest-neighbor queires over uncertain data[C]//Proceedings of the IEEE 24th Conference on Data Engineering (ICDE'08). Cancún: IEEE, 2008. |
| [7] | 朱怀杰, 王佳英, 王斌, 等. 障碍空间中保持位置隐私的最近邻查询方法[J]. 计算机研究与发展 , 2014, 51 (1) :115–125. Zhu Huaijie, Wang Jiaying, Wang Bin, et al. Location privacy preserving obstructed nearest neighbor queries[J]. Journal of Computer Research and Development , 2014, 51 (1) :115–125. |
| [8] | Brinkho T. A framework for generating network-based moving objects[J]. GeoInformatica , 2002, 6 (2) :153–180. doi:10.1023/A:1015231126594 |


