为了研究大口径反射镜紧缩场系统中板间缝隙对静区特性的影响,先采用空域法进行分析,根据空域仿真结果选择合适的拼接方式,并以此方式再进行时域和角域仿真.时域和角域中可做到主波与干扰波的分离,比较不同观察点的时域图和不同观察平面的角域图中的干扰波,最后得到较理想的静区范围.这种分析方法对于分析大型紧缩场中板间缝隙对静区特性的影响是有效的.
In order to study the impact of the the panel gap on quiet zone characteristics in the large compact antenna test range (CATR) systems, spatial domain method is adopted firstly, and an appropriate means of joining together is chosen according to the spatial simulation results, in this way, time and angular domain results are simulated then. Time and angular domain simulation can separate interference wave from main wave, comparing the interference wave of different points in the time and angular domain the reasonable range of ideal quiet zone can be obtained. This kind of analysis is efficient for analyzing the impact of the panel gap on quiet zone characteristics in the large CATR.
紧缩场(CR,compact range)系统能在较小的空间内产生准平面波,不仅没有远场测量的长距离要求,而且解决了大气吸收的问题,同时在室内建造紧缩场系统,可有效地控制背景辐射,且还能控制温度等一系列的参数,满足不同的工作系统要求. 然而随着太赫兹技术的发展,高频电大尺寸天线系统的辐射特性测试迫使紧缩场朝着高频率、大口径方向发展. 大口径紧缩场一般由多块反射面板拼接而成,面板拼接必然会产生板间缝隙,直接影响反射面的面形精度. 对于有限大的小面板,在面板间必然会产生额外的衍射波,这将影响紧缩场静区性能[1]. 为分析拼接缝隙对静区的影响,葛俊祥等[2]采用等效磁流法和菲涅尔近似积分法对大型双柱面紧缩场的拼缝进行分析,结果显示,当拼接缝隙宽度小于最小工作波长的十分之一时,缝隙对静区的影响可忽略. 周国锋等[3]针对典型的紧缩场反射面分割形式,在评价边缘轮廓度的基础上提出了统一的边缘干涉误差的计算模型,并对紧缩场整体拼缝进行预估和修正.
笔者针对三反射镜紧缩场天线测量系统,研究大口径主镜中的拼接缝隙对紧缩场静区特性的影响,以拼接缝隙宽度为1 mm为例,根据静区空域图的幅度波动找出最佳拼接方式,以此方式在时域中进行主波与干扰波分离以比较不同观察点时域图中的干扰波,同时在角域中比较不同观察平面的波谱特性,为合理的选择较理想静区作指导.
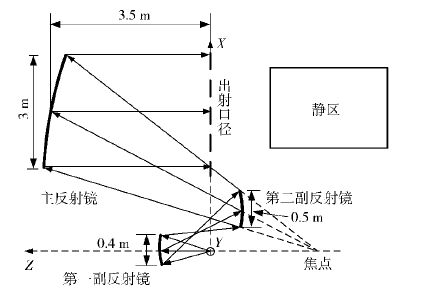
1 主镜为3 m口径的三反射镜紧缩场天线测量系统3 m口径三反射镜紧缩场系统[4]的结构如图 1所示. 整套系统由2个口径较小赋形反射面和1个口径为3 m的抛物面组成. 整套系统在商业软件通用反射面天线软件包(GRASP,general reflector antenna software package)里运用物理光学(PO,physical optics)和物理绕射理论(PTD,physical theory of diffraction)算法仿真,馈源照射赋形镜1,形成表面电流,接着赋形镜1又作为发射源将电磁波辐射到赋形镜2上,依次进行,直到得出出射静区. 图 2为这套紧缩场系统在仿真频率为70 GHz时的静区空域幅度. 从图 2可以看出,2.1 m口径静区内幅度波动为0.58 dB.
|
图 1 3 m口径三反射镜紧缩场结构图 |

|
图 2 3 m口径三反紧缩场静区空域幅度 |
由于抛物面口径已经达到了3 m,这对于加工整块板子来说难度很大且面形精度也很难达到要求. 这里可采用多块面板拼接形成3 m口径反射面,又由于反射面在XOY平面投影为矩形,所以可将反射面分割为若干个矩形小面板. 在面板间必然会产生额外的衍射波,这将影响三反射镜紧缩场静区性能,如何分析来自板间缝隙的衍射波对静区的影响是下面工作的重点.
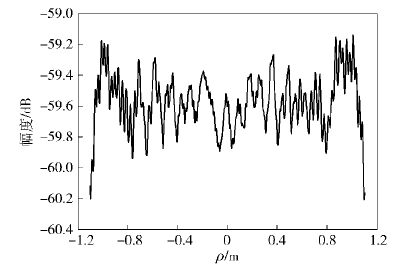
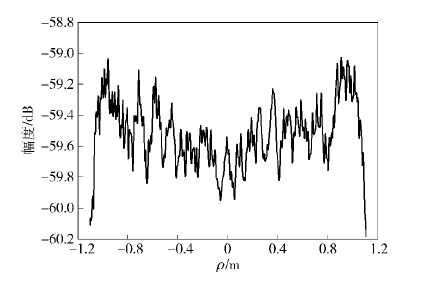
为了分析缝隙衍射波对静区的影响,首先要考虑合理的反射面分割方式. 通常,反射面可被分割为4块、9块或16块. 这3种分割方法的XOY面投影图分别为4块1.5 m×1.5 m,9块1 m×1 m,16块0.75 m×0.75 m的小矩形. 取各个面板间缝隙均为1 mm,静区距离口径中心6 m,工作频率70 GHz时,3种分割方式的静区空域幅度仿真图如图 3~图 5所示.
|
图 3 4块面板的静区空域幅度 |

|
图 4 9块面板的静区空域幅度 |
|
图 5 16块面板的静区空域幅度 |
从图 3~图 5可以看出,在2.1 m口径静区内,4块、9块、16块面板的静区幅度波动分别为0.8 dB、0.89 dB、0.92 dB. 与图 2中的整块反射面仿真结果对比可以得到,在静区范围相同时,随着面板数、板间缝隙数的增加,静区幅度波动不断增大,而这正是由于面板间的复杂衍射波引起的.
对于反射面分块方式,若反射面分为4块面板,则每块面板的半径太大因而加工困难,若反射面分为16块,虽然每块面板口径变小,但会增加板间缝隙个数,进而增加衍射波. 因此,结合实际加工,分为9块面板的可行性最高.
鉴于必然存在的衍射波,在空域图中已经看到衍射波对静区幅度波动的干扰,接下来以9块面板的分块方式继续在时域和角域中分别分析板间衍射波对静区的影响.
3 时域分析缝隙对静区的影响根据衍射理论,辐射场可看作口径直射波与面板间衍射波的综合. 为了区分直射波和衍射波[5-7],将空域谱转换到时域谱. 空域中任意一点的场都可表示为E(f). 可通过逆向傅里叶变换得到时域场[8]为
| $e\left( \tau \right)={{\int }_{-\infty }}^{\infty }E(f)exp~(j2\pi f\tau )df~$ | (1) |
其中:c为自由空间光速,τ为经过距离r后的延迟时间,即从辐射源到静区观察点的延迟时间.
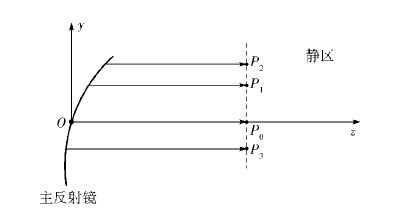
选取的静区观察点为P0、P1、P2、P3,如图 6所示. P0O为6 m. P1,P2在P0的正上方,P3在P0的正下方. P1P0、P2P0、P3P0分别为1 m、1.2 m、1 m. 频率范围为70~100 GHz,频域的采样点数为301. 缝隙宽度分别取0、1 mm. 这里,为了降低旁瓣波动,更直观地分辨出主波和干扰波,选取反变换的时域点数为310.
|
图 6 静区时域观察点 |
图 7和图 8分别为P0点和P1点的时域谱. 可清晰看到主波在0.02 μs到达P0点. 有干扰波在主波之前到达,一般只可能是由于馈源的直漏场造成的. 在0.13 μs时刻,缝隙宽度为1 mm的波形明显出现几路干扰波,这正是由于面板间缝隙衍射引起的. 然而干扰波幅度小于主波幅度30 dB,这可能是1 mm的缝隙相对于3 m口径过小的缘故.

|
图 7 P0点的时域谱 |
|
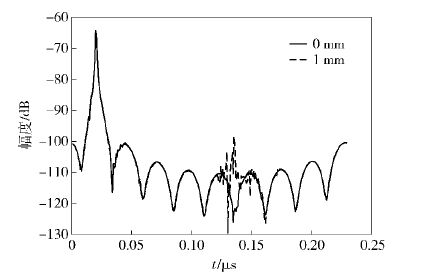
图 8 P1点的时域谱 |
图 9为P2点的时域谱. 由于三反紧缩场静区利用率一般为70%,而此时的P2点已经在静区之外,从图 9可以看到板间缝隙引起的干扰波明显增大.

|
图 9 P2点的时域谱 |
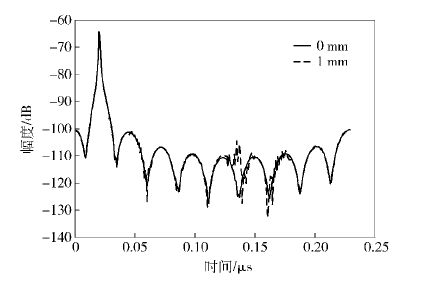
图 10为P3点的时域谱. 波形与P0点类似,主波在0.02 μs处,在主波前到达的由于馈源直漏场造成的干扰波并没有变化,面板间缝隙衍射引起的干扰波在0.125 μs处.
|
图 10 P3点的时域谱 |
根据平面波谱理论,观察面的场也可看作是由口径不同辐射方向的平面波的综合[8]. 假设观察平面相应的平面波角谱为G(kx,ky),它可表示为
| $G({{k}_{x}},{{k}_{y}})={{\int }_{-\infty }}^{+\infty }{{\int }_{-\infty }}^{+\infty }E\left( x,y \right)exp~[j({{k}_{x}}x+{{k}_{y}}y)]dxdy$ | (2) |
其中:kx=k0sin θcos Φ,ky=k0sin θsin Φ. G可看作E的逆向傅里叶变换.
图 11为9块面板在6 m静区处XOY面的投影图. 首先要在投影平面做2维近场空域-角域转换. 横向范围为一个由P1P2限制的正方形区域,沿x轴、y轴对称分布. P1、P2、P3、P4、P5、P6沿x轴对称分布,且P1P2、P3P4、P5P6分别为4 m、3 m、2.1 m,仿真频率为70 GHz. 缝隙宽度分别取0、1 mm.

|
图 11 口径XOY投影图 |
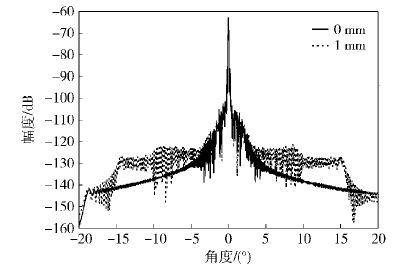
图 12为从2维结果中提取出的沿着P1P2的1维平面波角谱. 通带角估测为29°,大约就是口径边缘到静区观察中心的角度. 同时可以看到,在通带内因板间缝隙的存在,使波谱成分增加.
|
图 12 P1P2的角域图 |
图 13为从2维结果中提取出的沿着P3P4的1维平面波角谱. 可以看到波谱变得集中,且口径边缘衍射波被抑制. 但在±5°范围内产生了较多成分的干扰波,这个角度范围正是中心面板周围板间缝隙和观察平面中心夹角的范围.

|
图 13 P3P4的角域图 |
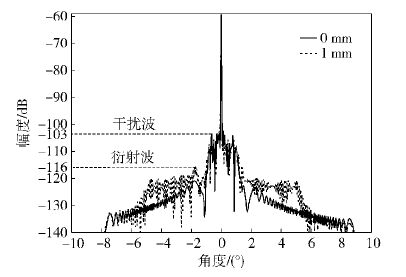
对于三反紧缩场,口径利用率通常为70%,这块区域用于放置被测天线. 因此,最后分析2.1 m口径的静区观察面. 图 14为从2维结果中提取出的沿着P5P6的1维平面波角谱. 可以看出,尽管波谱更加集中,但主波附近增生了很多干扰波,在缝隙宽度为1 mm时,最大增生干扰波、边缘衍射波相对于主波分别为-43 dB、-56 dB.
|
图 14 P5P6的角域图 |
分析缝隙对于静区性能特性影响,有利于了解大型三反紧缩场的整体性能. 用空域的分析方法可获得合适的分块方式,用时域和角域的分析方法,根据主波与干扰波到达静区的时间差异和角度差异,可分离主波和干扰波. 比较不同观察点的时域图和不同观察平面的角域图中干扰波的大小,对于合理选择理想静区有着指导意义. 笔者以主反射面为9块面板、板间缝隙取1 mm为例,从时域图和角域图中估算到此套紧缩场静区利用率为68%,这为实际反射面板拼接中的缝隙大小的控制起参考作用.
| [1] | Hüschelrath J. The electromagnetic problem of interpanel gaps inreflector antennas[J]. Acta Astronautica , 2005, 57 (2-8) :356–371. doi:10.1016/j.actaastro.2005.03.022 |
| [2] | 葛俊祥, 何国瑜, 江贤柞. 大型双柱面紧缩场天线缝隙的近场扰动[J]. 电子学报 , 1997, 25 (3) :25–28. Ge Junxiang, He Guoyu, Jiang Xianzuo. The gaps scattering effect in a two-cylindrical compact antenna range[J]. Acta Electronica Sinica , 1997, 25 (3) :25–28. |
| [3] | 周国锋, 李晓星, 栾京东, 等. 大型紧缩场边缘干涉误差检测及拼缝修正[J]. 北京航空航天大学学报 , 2014 (2) :166–171. Zhou Guofeng, Li Xiaoxing, Luan Jingdong, et al. Edges interference errordetection and reflector gaps correction for large-scale compact range[J]. Journal of Beijing University of Aeronautics and Astronautics , 2014 (2) :166–171. |
| [4] | Yang Cheng, Yu Junsheng, Yao Yuan, et al. Numerical synthesis of tri-reflector CATR with high cross-polarization isolation[J]. Electronics Letters , 2016 . |
| [5] | Quan Shaohui, Liu Qinghui. Near-field radiation characteristics of shaped electrically large apertures in the spatial and angular domains[J]. IET Microw, Antennas, Propag , 2010, 4 (11) :1838–1846. doi:10.1049/iet-map.2009.0423 |
| [6] | Quan Shaohui. Spatial and angular domain analysis of the near-field radiation of electrically large apertures with non-uniform field[J]. IET Microwaves, Antennas and Propagation , 2012, 6 (2) :178–185. doi:10.1049/iet-map.2011.0133 |
| [7] | Quan Shaohui. Time domain analysis of the near-field radiation of shaped electrically large apertures[J]. IEEE Trans Antennas Propag , 2010, 58 (2) :300–306. doi:10.1109/TAP.2009.2037705 |
| [8] | 全绍辉, 何国瑜, 徐永斌. 紧缩场干扰波的时域分析[J]. 电波科学学报 , 2003 (4) :389–392. Quan Shaohui, He Guoyu, Xu Yongbin. CATR extraneous waves analysis using time domain approach[J]. Chinese Journal of Radio Science , 2003 (4) :389–392. |


