2. 西南石油大学 计算机科学学院, 成都 610500
提出了一种基于蝙蝠算法的目标跟踪新方法.首先描述了基于蝙蝠算法的目标跟踪流程,在此基础上研究了蝙蝠算法的迭代终止条件、蝙蝠种群数、脉冲频率因子和脉冲音强衰减因子对跟踪性能的影响,并通过实验确定了以上参数,最后与粒子滤波、均值漂移和粒子群优化3种跟踪算法进行了比较.实验结果表明,基于蝙蝠算法的视频目标跟踪方法的跟踪效果优于其他3种算法.
2. School of Computer Science, Southwest Petroleum University, Chengdu 610500, China
A new visual tracking method based on bat algorithm (BA) was presented, in which, the BA-based tracking architecture is proposed. Then, the impact of the iterative termination condition, population size, pulse frequency increasing coefficient and pulse amplitude attenuation coefficient on the tracking performance are studied and these parameters are determined. To demonstrate the tracking ability of the proposed tracker, comparative studies of tracking accuracy and speed of the BA-based tracker with three representative trackers, namely, particle filter, meanshift, particle swarm optimization are given. Comparative results show that the proposed algorithm outperforms the other three trackers.
目标跟踪在智能视频监控、人机交互、机器人视觉导航等领域中具有广阔的应用前景. 虽然研究人员对视觉跟踪的理论开展过大量研究[1-2],但由于复杂多变的外界环境,目标跟踪仍然是计算机视觉领域的研究热点和难点问题之一.
运动目标的特征建模和搜索策略是目标跟踪算法的2个关键因素. 近年来,特征建模技术获得了很大的发展[3]. 相比较目标建模,目标的搜索策略没有得到足够的重视. 根据目标搜索策略的不同,目标跟踪方法可分为基于确定性和概率性2种跟踪方法[4]. 基于确定性的跟踪方法以均值漂移[5]为代表. 基于概率性跟踪方法以粒子滤波为代表[6].
受均值漂移算法的启发,有学者采用智能优化算法来解决目标跟踪问题. Zhang等[7]将粒子群优化(PSO,particle swarm optimization)算法引入目标跟踪过程中,通过提高粒子的适应值,不断更新每个粒子自身的状态来控制粒子群的运动. Park等[8]提出了一种进化粒子滤波算法,通过交叉和变异算子解决粒子滤波中存在的粒子匮乏问题. Minami等[9]设计了一套基于遗传算法的目标跟踪算法,能实时地跟踪目标.
蝙蝠算法是由Yang提出的一种模拟蝙蝠回声定位行为的群智能优化算法[10]. 该算法具有模型简单、收敛速度快、可并行处理等特点,正在逐步被应用到优化领域. 笔者提出了一种基于蝙蝠算法的目标跟踪方法. 首先描述了基于蝙蝠算法的目标跟踪流程,在此基础上研究了蝙蝠算法的参数的敏感性和迭代终止条件,最后通过实验验证了笔者算法的有效性.
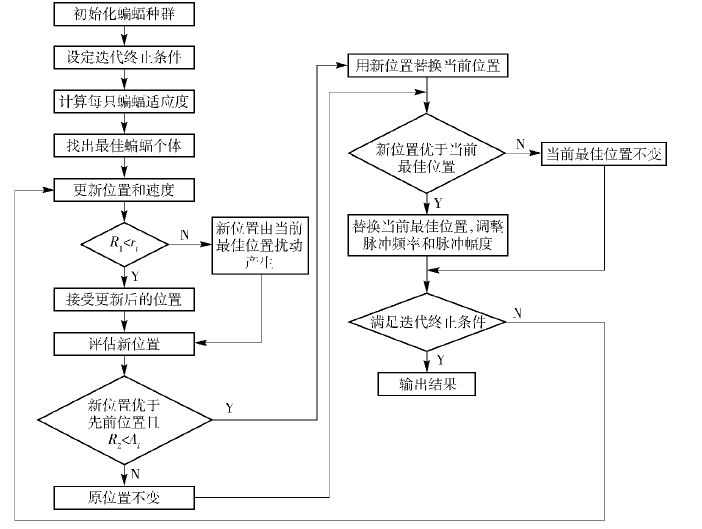
1 理论基础 1.1 蝙蝠算法通过模拟蝙蝠借助超声波搜索、捕食猎物的生物学特性,Yang提出一种基于随机优化的蝙蝠算法[10],具体流程如图 1所示.
|
图 1 蝙蝠算法流程 |
1) 初始化蝙蝠群. 包括种群大小N、蝙蝠个体飞行速度vi、脉冲频率ri0和脉冲音强Ai0.
2) 设置迭代终止条件.
3) 计算蝙蝠个体的适应度值.
4) 根据适应度对蝙蝠群排序,找出最优蝙蝠个体.
5) 对第i只蝙蝠的位置和速度进行更新为
| $~{{v}_{i}}^{t}={{v}_{i}}^{t-1}+({{x}_{i}}^{t}-{{x}^{*}}){{f}_{i}}$ | (1) |
| ${{x}_{i}}^{t}={{x}_{i}}^{t-1}+{{v}_{i}}^{t-1}$ | (2) |
其中:vit和vit-1分别为蝙蝠i在t-1和t时刻的飞行速度;xit为蝙蝠i在t时刻的空间位置,x*为在当前群体中最佳蝙蝠所处位置;fi∈[fmin ,fmax ]为搜索脉冲频率范围.
6) 判断条件R1<ri. 其中R1∈[0, 1]为满足均匀分布的随机数. 如果满足条件,接受更新后的位置. 否则,执行步骤7).
7) 新位置由当前最佳位置扰动产生,表示为
| ${{x}_{new}}~=~{{x}_{old}}+\varepsilon {{A}_{t}}$ | (3) |
其中:ε∈[-1,1]为一个服从均匀分布的随机数,At=〈Ait〉为在t时刻所有蝙蝠的平均响度.
8) 计算新位置的适应度值.
9) 判断新位置是否优于先前位置且满足R2<Ai,其中R2∈[0, 1]为满足均匀分布的随机数. 如果满足条件,新位置替换原来位置,否则,原位置不变.
10) 判断新位置是否优于当前最佳位置. 如果不满足条件,则当前最佳位置不变,否则,新位置替换当前最佳位置,并执行步骤11).
11) 调整脉冲频率和幅度为
| ${{r}_{i}}^{t+1}={{r}_{i}}^{0}[1-exp~\left( -\gamma t \right)]$ | (4) |
| ${{A}_{i}}^{t+1}=\alpha {{A}_{i}}^{t}$ | (5) |
其中:ri0为蝙蝠i的初始脉冲频率;rit+1为t+1时刻蝙蝠i的脉冲频率;γ为脉冲频度增加因子;Ait为t时刻蝙蝠i发射脉冲的音强;α为脉冲音强衰减因子.
12) 判断是否满足迭代终止条件. 如果满足,优化搜索结束,否则,继续执行步骤4).
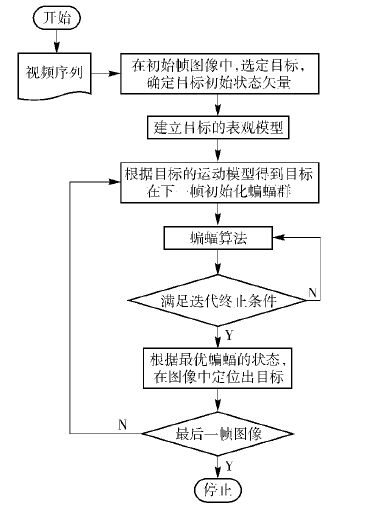
1.2 基于蝙蝠算法的目标跟踪笔者将视频目标跟踪看做蝙蝠群体捕捉食物的过程. 蝙蝠群对应图像中的候选目标区域,变量空间对应目标的状态空间,蝙蝠飞行速度对应目标状态的变化量,蝙蝠的搜索脉冲频率范围对应目标状态的变化范围,脉冲频率对应目标新状态由当前最佳状态产生的概率,脉冲音强对应目标新状态替换当前最佳状态的概率,蝙蝠个体的适应度值对应候选区域与目标的相似度,最佳蝙蝠状态对应目标状态. 基于此,笔者建立基于蝙蝠算法的目标跟踪方法. 具体流程如图 2所示.
|
图 2 基于蝙蝠算法的目标跟踪算法流程 |
1) 跟踪初始化
在视频图像中确定目标,并得到目标的初始状态矢量x=[x,y,s],其中(x,y)为目标外接框的中心点坐标,s为目标外接矩的缩放尺度.
2) 建立目标的表观模型
笔者的运动目标属于扩展目标,与传统的点目标跟踪的区别在于需要同时对运动目标的表观特征和质心运动学状态进行估计. 因此,首先需要对目标的表观特征进行建模. 笔者提取目标的核函数加权空间颜色模型[5]为
| ${{{\hat{p}}}_{c}}^{(u)}({{X}_{k}})=C\sum\limits_{i=1}^{M}{k}{{\left\| \frac{c-{{c}_{i}}}{r} \right\|}^{2}}\delta [b(ci)-u]$ | (6) |
其中:δ(·)为Delta函数;b(ci)为颜色量化函数,表示将位于ci处的像素颜色值量化并将其分配到颜色直方图相应的颜色等级索引中;u为直方图中颜色等级索引;C为归一化因子;k(·)为核函数,表示为
| $k\left( \|r\| \right)=\text{ }\left\{ \begin{align} & 1-\|r{{\|}^{2}},\|r\|<1 \\ & \text{ }0,其他 \\ \end{align} \right.$ | (7) |
其中:‖r‖为像素距离目标中心的距离.
3) 根据目标运动模型,初始化蝙蝠群.
考虑到目标运动具有随机性特点,笔者采用随机游走运动模型为
| $x{{\prime }_{i}}=x+{{s}_{k}}\left( r-0.5 \right)$ | (8) |
其中:x为目标的状态矢量,x′i为蝙蝠群中第i只蝙蝠的状态矢量,sk为步长因子,r为满足[0, 1]均匀分布的随机数. sk对应的各分量分别取20,20,0.4.
计算目标区域和候选区域的Bhattacharyya系数,得到蝙蝠个体的适应度值为
| ${{\rho }_{BC}}\left( p,q \right)=\underset{i=1}{\overset{m}{\mathop{\sum }}}\,\sqrt{{{p}_{i}}{{q}_{i}}~}$ | (9) |
其中:p和q为目标和候选区域的核函数加权空间颜色直方图,m=512为颜色分块数.
4) 通过蝙蝠算法不断地优化蝙蝠个体的状态
在不满足迭代终止条件情况下,采用2.1节描述的蝙蝠算法不断地优化蝙蝠个体的状态. 蝙蝠个体的状态矢量按照式(1)~式(3)进行更新. 其中,搜索脉冲频率范围fi的(x,y)分量的取值范围为[-10, 10],s的取值范围为[0.8,1.2]. 脉冲频率和幅度按照式(4)和式(5)进行调整.
5) 定位目标
得到适应度最大(最优)的蝙蝠个体,并根据最优蝙蝠个体状态矢量,在图像中定位出目标位置.
6) 判断视频中是否有新图像输入,如果有,则继续执行步骤3),否则,跟踪结束.
2 参数设定 2.1 迭代终止条件迭代终止条件包括以下3种方式,如果其中任何1个条件成立,迭代优化过程终止. 3个迭代终止条件定义如下.
条件1 总迭代次数达到设定的最大迭代次数. 该条件确保目标跟踪结果的准确性,笔者设定最大的迭代次数为500.
条件2 蝙蝠群体中最优个体的适应值好于某一设定的阈值T1,且群体中最优和最差的个体的距离小于设定的阈值T2. 该条件中T1和T2两个阈值同时作用,可使蝙蝠群体的所有个体聚集到最优解附近. 取T1=0.8,T2=5.
条件3 连续无效迭代次数超过设定的阈值. 如果连续无效迭代的次数超过某一限制,说明整个迭代收敛速度过慢,或目标已经丢失. 在这种情况下,为了节省时间,迭代提前终止. 假设连续无效迭代次数为总迭代次数的1/3.
2.2 优化参数确定笔者选取一段具挑战性的测试视频,如图 5(b)所示,研究蝙蝠种群大小、脉冲频率因子和脉冲音强衰减因子对目标跟踪性能的影响,并确定在最少的迭代次数获得最精确解的参数值.
首先分析蝙蝠种群大小对目标跟踪性能的影响. 笔者将种群数从5增加到50. 图 3描述了蝙蝠群体大小对目标跟踪准确度和消耗时间的影响.

|
图 3 蝙蝠种群数对跟踪性能的影响 |
通过分析图 3可以发现,跟踪消耗的时间随着种群数的增加而不断增加. 但跟踪过程中目标丢失的个数,存在2个不同的阶段. 当种群数在[5, 20]区间,随着种群数的增加,目标丢失的数目逐渐减少,表明跟踪精度逐渐提高. 当种群数在[20, 50]区间,跟踪精度趋于稳定. 综合考虑跟踪精度和消耗时间,蝙蝠种群数为20.
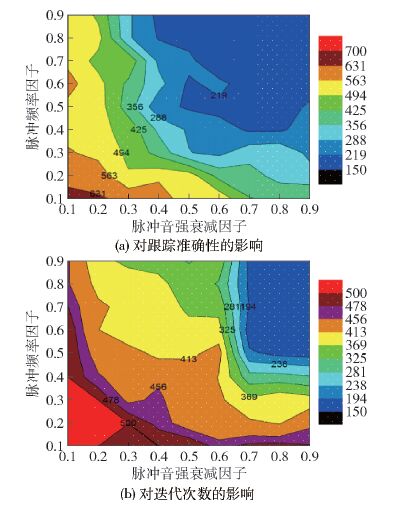
其次,分析脉冲频率因子γ,脉冲音强衰减因子α对目标跟踪性能的影响. 笔者将γ和α分别在范围(0,1)内采样,采样间隔均为0.1. 在测试过程中,首先考虑目标跟踪的准确性,再考虑跟踪过程需要的时间. 图 4描述了γ和α对目标跟踪的影响.
|
图 4 脉冲频率因子和音强衰减因子对目标跟踪的影响 |
通过图 4可以看出,当γ∈[0.4,0.9],α∈[0.5,0.9]时,目标丢失数目较少,跟踪准确度较高. 当γ∈[0.5,0.9],α∈[0.7,0.9]时,迭代次数较少,跟踪速度较快. 综合考虑跟踪准确度和消耗时间,取γ =0.8,α =0.8.
3 实验结果与分析为了验证笔者算法的有效性,将笔者方法与均值漂移算法[5]、粒子滤波算法[6]和粒子群优化算法[7]进行比较. 笔者选取了6个具有挑战性的测试视频,如图 5所示.

|
图 5 跟踪测试序列中的典型图像 |
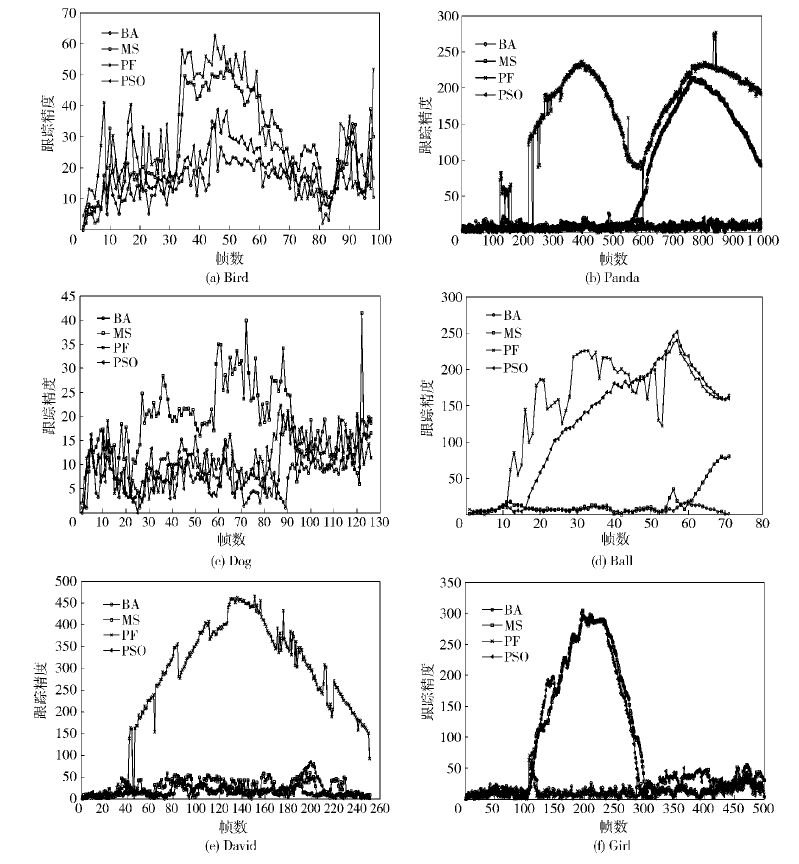
计算出几种跟踪方法的跟踪结果与真实目标的欧氏距离(单位:像素)衡量跟踪的精度. 实验结果如图 6所示.
|
图 6 算法在不同视频序列的跟踪结果 |
通过图 6可以看出,笔者方法能在上述难点因素下成功地跟踪上目标. 基于粒子群优化的跟踪算法在“Girl”和“Ball”测试视频中丢失了目标. 均值漂移算法在“David”测试视频中能成功跟踪目标,但在其余测试序列中目标出现了丢失. 粒子滤波算法能在“Girl”和“Dog”测试视频中跟踪较为理想,但在其余测试视频中跟踪效果较差.
为了验证算法的时间性能,统计了4种算法在跟踪过程中的平均时间消耗,结果如表 1所示.
从表 1可以看出,对于“Girl”、“Panda”和“Ball”视频,笔者算法的平均时间消耗略多于均值漂移算法. 但相比较粒子滤波和粒子群优化算法,笔者算法速度较快.
|
|
表 1 算法的平均时间消耗 |
提出了一种基于蝙蝠算法的视觉跟踪方法,在图像序列中快速准确地跟踪目标. 实验结果表明,笔者方法计算量小,抗干扰能力强,跟踪效果优于粒子滤波算法、均值漂移算法和粒子群优化算法. 在基于蝙蝠算法的目标跟踪框架下,融合更加有效的特征和相应的特征度量方法,并实现多目标跟踪是后续研究的重点.
| [1] | Wu Yi, Lim Jongwoo, Yang Minghsuan. Object tracking benchmark[J]. IEEE T Pattern Anal , 2015, 37 (9) :1834–1848. doi:10.1109/TPAMI.2014.2388226 |
| [2] | 侯志强, 韩崇昭. 视觉跟踪技术综述[J]. 自动化学报 , 2006, 32 (2) :603–617. Hou Zhiqiang, Han Chongzhao. A survey on visual tracking[J]. Acta Automatica Sinica , 2006, 32 (2) :603–617. |
| [3] | Li Xi, Hu Weiming, Shen Chunhua, et al. A survey of appearance models in visual object tracking[J]. ACM T Intel Syst Tec , 2013, 4 (4) :58. |
| [4] | Gao Mingliang, He Xiaohai, Luo Daisheng, et al. Object tracking based on harmony search: comparative study[J]. J Electron Imaging , 2012, 1 (4) :43001. |
| [5] | Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking[J]. IEEE T Pattern Anal , 2003, 25 (5) :564–577. doi:10.1109/TPAMI.2003.1195991 |
| [6] | Isard M, Blake A. Condensation-conditional density propagation for visual tracking[J]. INT J Comput Vision , 1998, 29 (1) :5–28. doi:10.1023/A:1008078328650 |
| [7] | Zhang Xiaoqin, Hu Weiming, Maybank S, et al. Sequential particle swarm optimization for visual tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Anchorage. 2008: 1-8. |
| [8] | Park S, Hwang J P, Kim E, et al. A new evolutionary particle filter for the prevention of sample impoverishment[J]. IEEE T Evolut Comput , 2009, 13 (4) :801–809. doi:10.1109/TEVC.2008.2011729 |
| [9] | Minami M, Agbanhan J, Asakura T. Manipulator visual servoing and tracking of fish using a genetic algorithm[J]. Industrial Robot-an International Journal , 1999, 26 (4) :278–289. doi:10.1108/01439919910277549 |
| [10] | Yang Xinshe. A new metaheuristic bat-inspired algorithm[C]//Nature Inspired Cooperative Strategies for Optimization. Berlin: Springer Verlag, 2010, 284: 65-74. |


