针对室内无线传感器网络通信传输不稳定和定位精度较差的情况,提出了一种移动机器人自主动态定位系统,通过实时选择邻近信标节点,确定节点坐标构成的边界,绘制局部网格空间,实现机器人动态定位.利用接收信号强度指标实现测距,然后采用基于测距的改进近似三角形内点测试(APIT)算法完成定位,再使用卡尔曼算法修正定位误差.该方法适用于室内网络传输不稳定的实际情况,采用卡尔曼滤波器获得最优数据.实验结果表明,该移动机器人自主动态定位方法比基于网格的极大似然方法具有更好的精度和适应性.
According to the communication instability and poor localization accuracy in indoor wireless sensor networks, a dynamic localization of mobile robot was proposed which dynamically chooses neighbor beacon nodes and establish grid space based on boundary of beacon node location in real time. This method applies the receive signal strength index for distance measurement. Furthermore, the range-based improved approximate point in triangle test (APIT) was used to realize the localization. Finally, the localization error-correct is implemented by the classical Kalman filter. The method is adaptable for the communication instability of indoor wireless sensor networks, the Kalman filter provides optimal data. Experiments show that the accuracy and adaptability of the dynamic localization of the mobile robot are better than Kalman filter grid-based improved maximum likelihood estimation algorithm.
移动机器人动态定位是无线传感器网络技术中的重要研究领域. 无线传感器网络能够在部分节点损毁的情况下实现动态自组织[1-2],可以在灾难救援系统中,为机器人提供不间断的实时环境数据,有效保障机器人的感知和救援能力. 无线传感器网络定位算法按照是否需要测量距离信息可以分为基于测距[3-5]和距离无关[6-7]2种. 前者计算实际距离信息,定位精度较高;后者相对定位误差较大,但是节点能耗较小.
近似三角形内点测试(APIT,approximate point in triangle test)定位算法在大规模传感器网络中得到广泛应用[7]. 由于传感器节点的成本和硬件设备的限制,通过点到点的距离估计完成基于测距的定位算法是一种成本代价较高的解决方案. 对于精度要求不高的传感器网络应用,APIT是一种成本有效的替代方案. 然而,在室内灾难救援系统中,房间空间较小,通道狭小,定位精度要求较高;并且,由于移动机器人硬件设备完善,能量充足,能够承担主要的计算任务. 因此,以机器人为中心的实时集中式计算任务分发成为可行方案. 为了更好地扩充移动机器人自主动态定位算法,在已有的极大似然定位算法的基础上[3-4],笔者针对距离无关的APIT算法进行改进,实现由距离无关到基于点对点测距的定位算法,有效提高了定位精度,成为极大似然定位算法之外,一种有效的移动机器人实时自主动态定位算法.
针对室内网络环境复杂多变的情况,采用基于接收信号强度指标(RSSI,receive signal strength index)的测距方法,引入信标节点辅助定位,能量充沛的移动机器人集中完成所有定位计算. 针对距离无关的APIT定位算法误差较大、计算成本较高的情况,提出实时遴选邻近信标节点对网格空间进行改进. 针对RSSI易受室内环境影响的情况,采用卡尔曼滤波算法修正定位误差. 实验结果表明,所提算法有效降低了测量噪声和定位误差,尤其在网络通信不稳定的室内环境中保证定位结果的准确性.
1 RSSI测距模型利用无线传感器周期性发射的无线信号强度随着传播距离增加而衰减的特性,在已知发送信号强度和接收信号强度的前提下,通过数学模型将损耗转换为距离,从而确定发送节点和接收节点之间的估计距离.
根据实际应用的环境不同,RSSI测距表现出不同的变化特性,特别是密集部署的无线传感器网络中,反射、多径传播等复杂问题层出不穷. 在仿真过程中,采用经验公式[4]为
| ${{P}_{t}}(d)={{P}_{0}}({{d}_{0}})-10\eta lg\left( \frac{d}{{{d}_{0}}} \right)+{{X}_{\sigma }}$ | (1) |
其中:d为无线信号从发射节点到接收节点之间的传播距离;Pt(d)为RSSI数值,随着d的变化而变化;P0(d0)为距发射机d0处的参考信号强度;η为信号传播路径衰落系数,与特定环境相关;Xσ为由遮蔽效应引起的正态分布的随机变量.
根据本实验的场景要求,设置P0(d0)为-41.1 dBm;η取值为3;d0为1 m;Xσ为均值为0,方差为4的高斯白噪声分布随机噪声.
2 最佳三角形内点测试数学模型APIT定位算法是一种自主定位的非测距定位算法. 首先判断机器人与3个信标节点之间的相对位置,再获取3个信标节点的质心位置. 其相对位置判断依据是最佳三角形内点测试(PIT,prefect point-in-triangulation test)法.
1) 机器人在三角形内部
假设机器人处于三角形的内部. 从机器人角度观测,自己向任何方向移动时,会产生接近一个三角形顶点,而同时远离三角形其他顶点的情况.
2) 机器人在三角形外部
假设机器人处于三角形的外部. 从机器人角度观测,自己向某个特定方向移动时,会同时接近或远离三角形所有顶点.
根据上述分析,可以将机器人同时接近或远离顶点节点作为判断与三角形相对位置的条件. 通过遍历三角形顶点节点之外的所有邻近节点,搜索任何节点满足同时接近或远离三角形情况. 一旦存在一个节点实现从机器人当前位置移动到该节点位置,同时接近或者远离三角形顶点,就可以断定机器人位于三角形外部. 否则,机器人一定处于三角形内部.
3 基于测距的改进APIT算法基于测距的改进APIT定位算法实现了移动机器人实时动态定位. 移动机器人在运动过程中,周期性收集所有邻近信标节点的RSSI射频信号强度和坐标.通过RSSI测距数学模型转换成机器人与信标节点之间的距离. 然后穷尽搜索所有包含移动机器人的三角形区域,判断机器人是否处于三角形内部. 根据信标节点之间已知的坐标值,通过欧氏距离公式计算所有信标节点与构成三角形的信标节点之间的距离,从而确定机器人与三角形相对位置关系,并确定重叠次数最多的多边形区域,寻找该多边形的质心坐标作为移动机器人的估计位置.
按照每3个节点构成一组三角形的所有组合方式,基于PIT模型,搜索图中所有包含机器人的三角形数目. 然后,在包含机器人的三角形中,通过获取不规则交集区域缩小机器人出现的可能区域. 最后,通过计算交集区域质心估计机器人的位置.
在室内无线传感器网络中,信标节点周期性广播自身坐标,机器人通过邻近节点坐标与组成三角形的信标节点的坐标计算出邻近节点与三角形信标节点之间的距离,判断机器人自身是否在三角形内部,从而估计移动机器人可能的位置区域. APIT寻找所有三角形重叠区域缩小机器人可能存在的区域面积,通过估计重叠区域质心的位置作为移动机器人估计坐标.
1) APIT核心算法
融合邻近信标节点坐标和RSSI信息的APIT核心算法如图 1所示,通过遍历所有CN3种不同的三角形组合,计算机器人的估计位置.
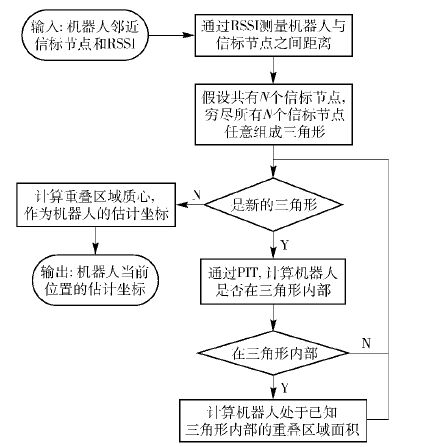
|
图 1 APIT核心算法流程 |
2) 改进APIT算法
APIT算法中使用的主要数学工具是建立无线传感器网络的矩阵网格区域,信标节点组成的三角形镶嵌到矩形网格区域中. 被占据的网格标注为特定数值,通过累计每个网格中标记的数值大小,确定重叠多边形区域,然后计算多边形区域的质心坐标作为估计节点坐标.
本算法以移动机器人为中心,探测以阈值为半径的区域内的所有信标节点;然后通过判断移动机器人是否在信标节点构成的三角形区域中,确定是否启动APIT算法. 在APIT算法启动的初始阶段,通过遍历机器人周围阈值区域内的信标节点坐标,寻找横坐标最小值和纵坐标最小值,以及横坐标最大值和纵坐标最大值,从而确定矩阵网格区域范围为
| ${{V}_{min~}}=[min\text{ }({{x}_{1}},{{x}_{2}},\ldots ,{{x}_{n}})min\text{ }({{y}_{1}},{{y}_{2}},\ldots ,{{y}_{n}})]$ | (2) |
| ${{V}_{max~}}=[max\text{ }({{x}_{1}},{{x}_{2}},\ldots ,{{x}_{n}})max\text{ }({{y}_{1}},{{y}_{2}},\ldots ,{{y}_{n}})]$ | (3) |
其中:Vmin为移动机器人周边动态矩阵网格区域左下角坐标,Vmax为矩阵区域右上角坐标,min(x1,x2,…,xn)为所有通信区域内信标节点横坐标最小值,min(y1,y2,…,yn)为纵坐标最小值,max(x1,x2,…,xn)为横坐标最大值,max(y1,y2,…,yn)为纵坐标最大值.
以左下角坐标和右上角坐标确定行数为100、列数为100的网格矩阵,计算每个网格的质心坐标为
| ${{D}_{i,j}}=\left[ {{x}_{min~}}+\frac{1.5}{100}i({{x}_{max~}}-{{x}_{min~}}){{y}_{min~}}+\frac{1.5}{100}j({{y}_{max~}}-{{y}_{min~}}) \right]$ | (4) |
其中:Di,j为第i行第j列网格质心坐标,i和j为1~100整数,xmin、ymin、xmax、ymax分别为横坐标和纵坐标的最小值和最大值.
网格质心的权值以0为基数. 如果网格质心所在区域与包含机器人在内的三角形区域重合,则网格质心的权值自加1. 如果网格质心与不包含机器人的三角形区域重合,则网格质心的权值自减1. 公式为
| ${{V}_{i,j}}=\text{ }\left\{ \begin{align} & {{V}_{i,j}}+1,若{{D}_{i,j}}\cap {{I}_{a,b,c}}=true \\ & {{V}_{i,j}}-1,若{{D}_{i,j}}\cap {{O}_{a,b,c}}=true \\ \end{align} \right.$ | (5) |
其中:Vi,j为第i行第j列网格质心的权值,Ia,b,c为由a、b、c信标节点构成的三角形中涵盖机器人位置的集合,Oa,b,c为由a、b、c信标节点构成的三角形中不包含机器人位置的集合.
移动机器人的估计坐标为网格质心权值最大的网格区域构成的多边形中的质心坐标,即获取网格质心权值最大的所有网格的集合. 然后,遍历集合中每个网格质心坐标的平均值. 该加权后的计算结果,就是机器人的近似位置,即
| ${{P}_{robot}}=\left[ \frac{1}{h}\underset{i=m}{\overset{m+h}{\mathop{\sum }}}\,{{D}_{i}}^{x}\frac{1}{h}\underset{j=n}{\overset{n+h}{\mathop{\sum }}}\,{{D}_{j}}^{y} \right]|max\text{ }({{V}_{a,b}})$ | (6) |
其中:Probort为移动机器人在基于测距的改进APIT (IAPIT,improved APIT)算法中的估计坐标点,max(Va,b)为所有网格中权值最大的所有网格质心的集合,h为最大权值质心的总数,Dix和Djy为权值最大的网格质心横坐标和纵坐标,m为集合中左下角网格的在x轴方向的起始下标,n为该网格在y轴方向的起始下标.
图 2描述了权值的计算方法. 所有网格初始权值为0. 三角形由网格构成. 如果机器人出现在三角形内部,则对应三角形的所有网格权值加1;否则,相应网格权值减1. 通过遍历所有三角形区域,如图 2最高区域所示,确定最大网格集合的权值为3. 然后,计算该网格集合的质心,就是机器人的估计位置.
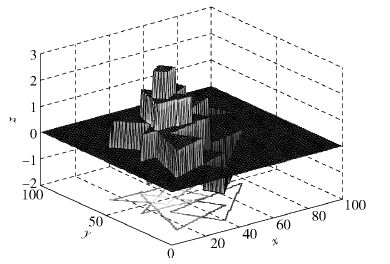
|
图 2 APIT算法的网格权重 |
如图 2所示,机器人当前时刻的IAPIT算法估计值只与机器人当前位置的无线传感器网络环境有关,与机器人前一时刻的网络环境无关. 机器人实时收集当前时刻相邻信标节点到达机器人无线传播信号的RSSI数值和信标节点坐标. 穷尽所有信标节点任意组成三角形,通过PIT数学模型首先计算机器人是否处于三角形内部,然后计算机器人处于三角形内部的所有三角形重叠区域面积,最后计算重叠区域的质心,作为计算机的估计坐标. 该计算过程只与机器人当前时刻周围信标节点的网络情况有关,而与机器人前一时刻的网络情况无关,所以不存在定位算法的累积误差情况.
4 适用于网络盲区的卡尔曼滤波算法当移动机器人运动在信标节点充足的无线传感器网络环境中时,基于测距的IAPIT定位算法可以提供误差微小的高精度定位. 但是,当移动机器人进入到信标节点贫乏的无线传感器网络时,基于测距的IAPIT定位算法将严重失真,甚至会导致整个定位估计严重偏离真实位置. 为此,采用针对网络盲区的卡尔曼滤波算法[4]提高定位精度.
其中,卡尔曼滤波的观测方程为所提出的IAPIT定位算法得到的估计坐标Zk. 首先,通过卡尔曼滤波预测方法估计下一时刻的机器人出现的估计位置 AX^U2 k+1/k,再使用状态更新方程完成卡尔曼增益Kk+1的更新;其次,为了防止定位算法出现严重偏离实际位置的情况,采用误差控制方程严格限定噪声uk+1/k的波动幅度,实现运动轨迹的平滑;最后,采用虚拟信标节点方法,实现机器人在网络盲区中的位置估计,保证定位算法的适应性.
5 移动机器人动态定位实验 5.1 仿真实验与结果分析在室内环境中的20 m×20 m的区域内,以2 m间距按照网格结构部署信标节点,部署过程中存在小于0.2 m的随机误差. 移动机器人在网络空间随机运动,以0.1 s的周期进行采样.
机器人以0.5 m/s的速度随机移动,对100个采样点,计算IAPIT定位估计值. 100个采样点中最大运行时间为4.284 2 s,最小运行时间为1.613 3 s,平均时间为2.440 1 s. 在搭载较好计算装置的移动机器人上,IAPIT定位算法可以完成实时位置估计.
图 3描述了2种算法的定位误差累积分布概率情况. 基于测距的IAPIT算法可以控制50%的定位结果的误差范围在4 m以内,且90%以上的定位误差不超过8 m. 由于基于测距的IAPIT算法能够针对大型无线传感器网络环境中传感器节点密度较大情况进行充分的信息融化,因此其最大定位误差能控制在10 m以内. 而三边测量(TE,trilateration estimation)法则远远超出了这一界限.

|
图 3 随机网络中定位误差的累积分布概率 |
图 4描述了基于测距和距离无关的APIT定位算法的定位误差. 在随机部署40个信标节点的无线传感器网络中,信标节点的通信半径R=50 m,所提出的IAPIT定位算法误差为0.1R,而Li等[7]提出的距离无关的FIAPIT定位算法误差达到0.6R. 可见将距离无关定位算法改进为基于测距的定位算法,可以有效提升定位精度,适应室内机器人动态定位所需的精度要求.

|
图 4 基于测距和距离无关的APIT定位误差比较 |
实验环境为1 020 cm×630 cm的教学实验室房间. 室内人员较多,桌椅围绕墙壁摆放,仪器设备和无线设备较为丰富,各种信号交互叠加效果明显. 为了实验数据准确,预先在天棚固定网格区域位置悬挂CC2530信标节点. 地面特点区域标注了自主定位节点将会到达的位置标识. 为了避免地面反射效果的严重影响,CC2530自主定位节点选择在距离地面50 cm高度采集测量数据. 自主定位节点与信标节点之间的垂直距离为112 cm.
针对室内无线传感器网络通信不稳定的问题,采用Feng等[4]的卡尔曼滤波方法修正定位误差,提出了卡尔曼滤波的IAPIT (KIAPIT,Kalman filter IAPIT)算法,适应室内环境对RSSI的影响,并与Feng等[4]的卡尔曼滤波的改进极大似然(KIMLE,Kalman filter improved maximum likelihood estimation)算法、经过卡尔曼优化RSSI测距精度的KIMLE (KRKIMLE,Kalman filter optimizing RSSI ranging and Kalman filter improved maximum likelihood estimation)算法和卡尔曼滤波的基于网格的改进极大似然(KGIML,Kalman filter grid-based improved maximum likelihood estimation)算法进行比较. 而经过卡尔曼优化RSSI测距精度的KIAPIT (KRKIAPIT)算法融合了KRKIMLE算法中的测距平滑思想,希望改进定位精度.
在实际应用中,房间内一般部署4个信标节点. 本实验设计了网格部署4个信标节点的场景. 图 5描述了4个信标节点场景中卡尔曼滤波算法的误差累积分布情况. 由于KIAPIT算法中的PIT算法对于网格部署4个信标节点场景效果最好,因而定位精度最高. KRKIAPIT算法反而会增加定位误差,而其他算法虽然定位效果较好,都不能达到KIAPIT算法的定位精度水平.

|
图 5 卡尔曼滤波算法在4个信标节点中的误差累积分布 |
针对复杂多变的室内无线传感器网络环境进行研究,提出了基于测距的APIT实时动态定位算法. 该方法有效融合了邻近信标节点的位置信息,实现了移动机器人的自主定位. 实验结果表明,该方法具有定位精度高和现场实现简单等特点,可以扩展用于真实环境下的灾害救援体系.
| [1] | 任倩倩, 孙蓓蓓, 刘勇, 等. 无线传感器网络动态环结构下目标信息收集方法[J]. 北京邮电大学学报 , 2016, 39 (1) :58–62. Ren Qianqian, Sun Beibei, Liu Yong, et al. A circular structure based information collection algorithm in wireless sensor networks[J]. Journal of Beijing University of Posts and Telecommunication , 2016, 39 (1) :58–62. |
| [2] | 章曙光, 周学海, 杨峰, 等. 无线传感器网络中防范选择性丢弃的途中过滤策略[J]. 北京邮电大学学报 , 2016, 39 (1) :68–73. Zhang Shuguang, Zhou Xuehai, Yang Feng, et al. En-route filtering strategy against selective discarding in wireless sensor networks[J]. Journal of Beijing University of Posts and Telecommunication , 2016, 39 (1) :68–73. |
| [3] | 吴成东, 冯晟, 张云洲. 基于异步卡尔曼滤波的移动机器人动态定位[J]. 东北大学学报(自然科学版) , 2013, 34 (3) :312–316. Wu Chengdong, Feng Sheng, Zhang Yunzhou. Dynamic localization of mobile robot based on asynchronous Kalman filter[J]. Journal of Northeastern University (Natural Science) , 2013, 34 (3) :312–316. |
| [4] | Feng Sheng, Wu Chengdong, Zhang Yunzhou, et al. Grid-based improved maximum likelihood estimation for dynamic localization of mobile robots[J]. International Journal of Distributed Sensor Networks , 2014, 11 (2014) :1–15. |
| [5] | Chu Hao, Wu Chengdong. A Kalman framework based mobile mode localization in rough environment using wireless sensor network[J]. International Journal of Distributed Sensor Networks , 2015 :1–9. |
| [6] | Ji Changpeng, Chen Meiling, Liu Qiao. Modified localization algorithm of APIT for WSN[J]. Instrument Technique and Sensor , 2012, 61 (8) :84–902. |
| [7] | Li Xiaofeng, Chen Liangfeng, Wang Jianping, et al. Fuzzy system and improved APIT (FIAPIT) combined range-free localization method for WSN[J]. KSII Transactions on Internet and Information Systems , 2015, 9 :2414–2434. |


