为了解决腹腔软组织电子计算机断层扫描影像难于分割的难题,提出一种基于格式塔认知框架的多目标分割算法.通过借鉴格式塔认知框架中“邻近度、相似度”的思想,引入超像素算法处理电子计算机断层扫描图像处理,生成可视块.进一步地,在可视块粒度描述有向邻接关系,以软组织的相对空间位置约束聚类分割过程.在公开数据库上的实验结果表明,该算法降低了聚类的计算量,其结果比当前流行的算法准确率更高.
In order to acquire better organ segmentation from abdominal computed tomography (CT) images, a multi-object segmentation algorithm based on cognitive framework is proposed. Inspired by the proximity and similarity idea in gestalt, super pixel concept of CT image processing has been produced. Specifically, by establishing the directed adjacency relationship of super-pixel, the spatial relationships of abdominal organs are modeled as prior knowledge to improve the classification accuracy. Experiments in public datasets illustrate that the proposed algorithm achieves better performance in either speed or accuracy than that of the state-of-art methods.
分割电子计算机断层扫描(CT,computed tomography)影像,识别目标器官是构造计算机辅助诊断系统的首要步骤[1]. 单纯利用形状、灰度等统计特性,难以获得良好的多目标分割结果[3-6]. 结合认知规律,利用计算机算法模仿医生识别软组织(肝、肾、胆囊、脾和动、静脉血管等)的行为过程,减少计算机因“图像灰度范围重叠、灰度不一致和人体器官生理蠕动”而受到的干扰[2].
笔者引入格式塔认知准则,通过综合形状、灰度特征[7],指导像素聚类过程. 将CT影像像素聚类结果定义为可视块. 结合相对空间约束关系,在可视块的粒度上进一步聚类,解决了腹腔软组织的多目标分类难题. 实验结果表明,笔者算法减少了分割迭代次数,和主流算法对比提高了准确率.
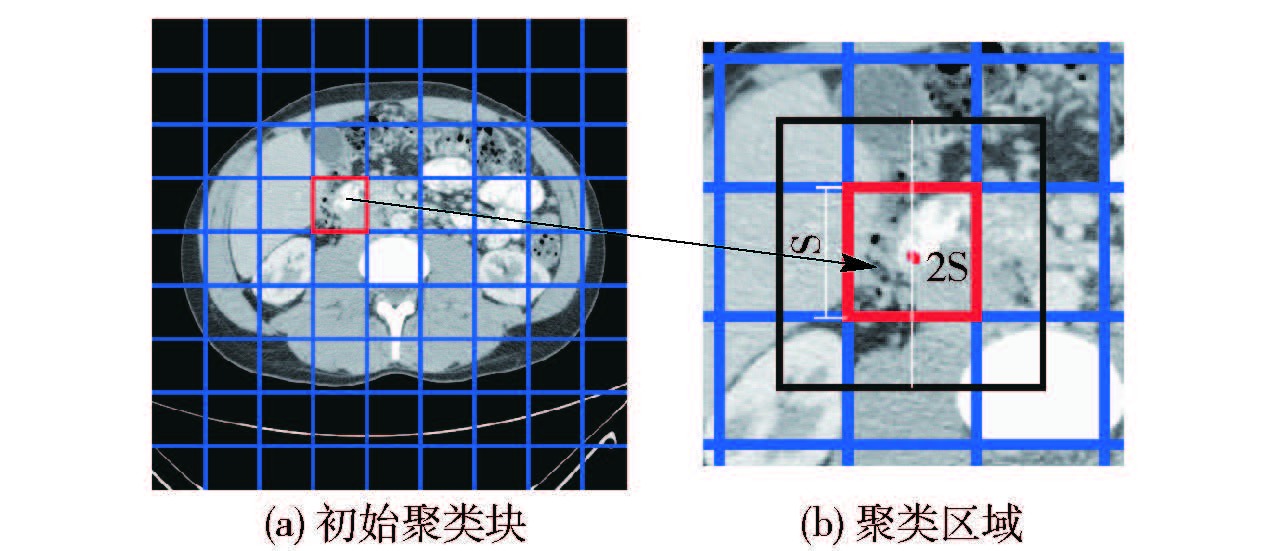
1 可视块的生成可视块是指影像中灰度相似、距离相近的像素集合. 要生成可视块,首先根据图像复杂的程度,设定K作为初始聚类中心数,生成如图 1(a)所示的K个初始矩形区域. 如果图像的分辨率为NM,每个可视块就包含了NM/K个像素. 每个矩形块的边长为S,$S=\sqrt{NN/K}$,即聚类范围为2S×2S,具体如图 1(b)所示.
|
图 1 可视块矩形区域生成规则图示 |
笔者采用的欧氏距离度量像素位置的邻近性,如式(1)所示. 采用像素灰度差的绝对值描述灰度相似性,如式(2)所示. 式(1)中的(x,y)分别代表像素点的横纵坐标,g为像素的灰度值,通过计算获得邻近度dxy和相似度dg.
综合邻近度、相似度,构成如式(3)所示的度量准则Ds,描述可视块的特征距离. 其中μ为控制像素紧密度的参数,μ越大,空间相似度贡献值越大,聚类也越紧密,通常将μ设置为影像中像素点亮度特征的标准差.
| ${{d}_{xy}}=\sqrt{{{({{x}_{i}}-{{x}_{j}})}^{2}}+{{({{y}_{i}}-{{y}_{j}})}^{2}}}$ | (1) |
| ${{d}_{g}}=|{{g}_{i}}-{{g}_{j}}|$ | (2) |
| ${{D}_{s}}=\frac{\mu }{S}{{d}_{xy}}+{{d}_{\text{Gray}}}$ | (3) |
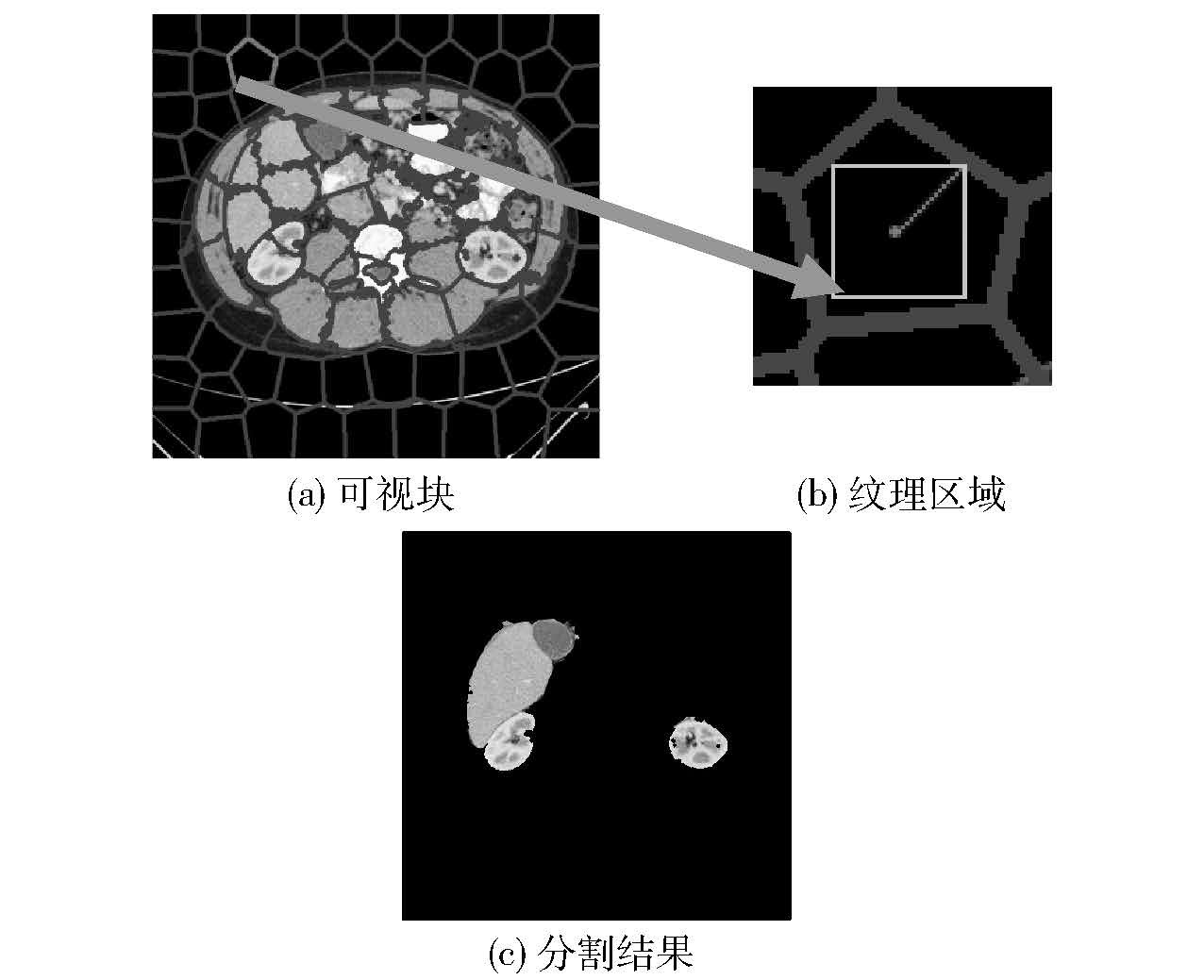
此外,笔者将初始矩形内梯度最小的像素点作为初始聚类中心,预设K=81,迭代上限次数为10. 基于可视块的特征距离,使用K-means聚类算法,迭代更新可视块轮廓,最终生成的可视块如图 2(a)所示.
|
图 2 生成可视块步骤 |
在格式塔心理学理论中,邻近度、相似度不仅能在像素点的粒度产生作用,使之聚合形成可视块,还能作用于可视块粒度,指导多目标分割. 而在可视块的粒度上,相似性度量的标准还增加了可视块的纹理特征及其相对空间位置. 在图 2(a)中,每个可视块内部像素隶属于同种组织,而每一个器官由若干可视块组成. 笔者以可视块作为基本单元描述有向邻接关系,用以描述软组织之间的相对空间关系;以灰度共生矩阵[8]提取可视块最大内接矩形区域的纹理特征,描述其可视块之间的相似度关系. 在此基础上,提出有监督学习算法的框架训练模型,对可视块进行分类.
为了获得灰度和纹理信息,首先定位可视块的中心点;然后在可视块边缘上找到距可视块中心最短距离的点,以该距离为定值找到可视块中面积最大的矩形,如图 2(b)所示;最后,采用灰度共生矩阵提取可视块的纹理特征. 与此同时,计算出可视块的灰度平均值作为代表灰度的值.
为了描述人体组织固有的空间相对关系,首先标记获得的可视块. 将肝、右肾、脾、胆囊、左肾、脊椎、背景分别标记为(1,2,3,4,5,6,0). 除了双肾外,具有相同标签的可视块彼此相连. 右肾与肝脏、胆囊较接近. 脾接近左肾,这两者都远离肝脏. 式(5)和式(6)的距离由式(4)定义,用来定义距离的远近. 由文献[5]和文献[7]可知,肝脏和脾脏位置比较稳定,且容易被定位. 因此,首先就能更精准地定位它们. 右肾、左肾的位置可由肝、脾的相对位置进行确定. 通过建立有向邻接关系,如图 3(c)所示,描述可视块之间的空间相对关系.

|
图 3 多目标分割示意 |
手动标记器官(肝脏、右肾、脾脏、胆囊、左肾)和脊椎的超像素块的标签,作为训练数据集. 它们的Label分别为自然数1~6,如图 3(b)所示. 规定其他区域标记为0. 可见,同一脏器的可视块相邻,肝脏与胆囊也是相邻;而右肾与肝脏相近,左右肾与脊椎相近. 通过式(4)描述可视块之间的邻近性.
| ${{d}_{\text{patch}}}=\|{{p}_{1}}-{{p}_{2}}{{\|}^{2}}$ | (4) |
| ${{d}_{\text{Neighbor}}}<2S$ | (5) |
| ${{d}_{\text{Close}}}<3S$ | (6) |
其中:dpatch为可视化块之间的距离,p1,p2分别为可视块中心像素点为(x1,y1),(x2,y2)的坐标,‖·‖为L2范式,S为可视块分割时初始聚类矩形块的边长,且满足式(5)就称可视块相邻,满足式(6)就称可视块相近.
在标记好的训练数据集基础上,以可视块粒度的邻近度、相似度,执行K-means算法对可视块进行分类,获得可视块的标签. 进一步地,利用空间相对关系修正可视块的标签信息. 算法分割图 2(a)和图 3(a)的结果如图 2(c)和图 3(d)所示. 以超像素块作为聚类单位,从512×512像素的图像变为大约9×9个的超像素块,聚类速度得到提升.
3 实验结果和分析为了验证笔者算法的适用性,特在公开数据集肿瘤影像档案(TCIA,the cancer imaging archive)验证相关算法,对比算法性能. 笔者选用了当前性能最好的阈值和梯度参数的函数(TG,function of threshold and gradient parameters)[5]、增强CT基于最大后验概率和最小体积重叠的定位(LVP,localization on contrast enhanced CT based on maximum a posteriori probability and minimum volume overlap)[6]算法作为对照实验组.
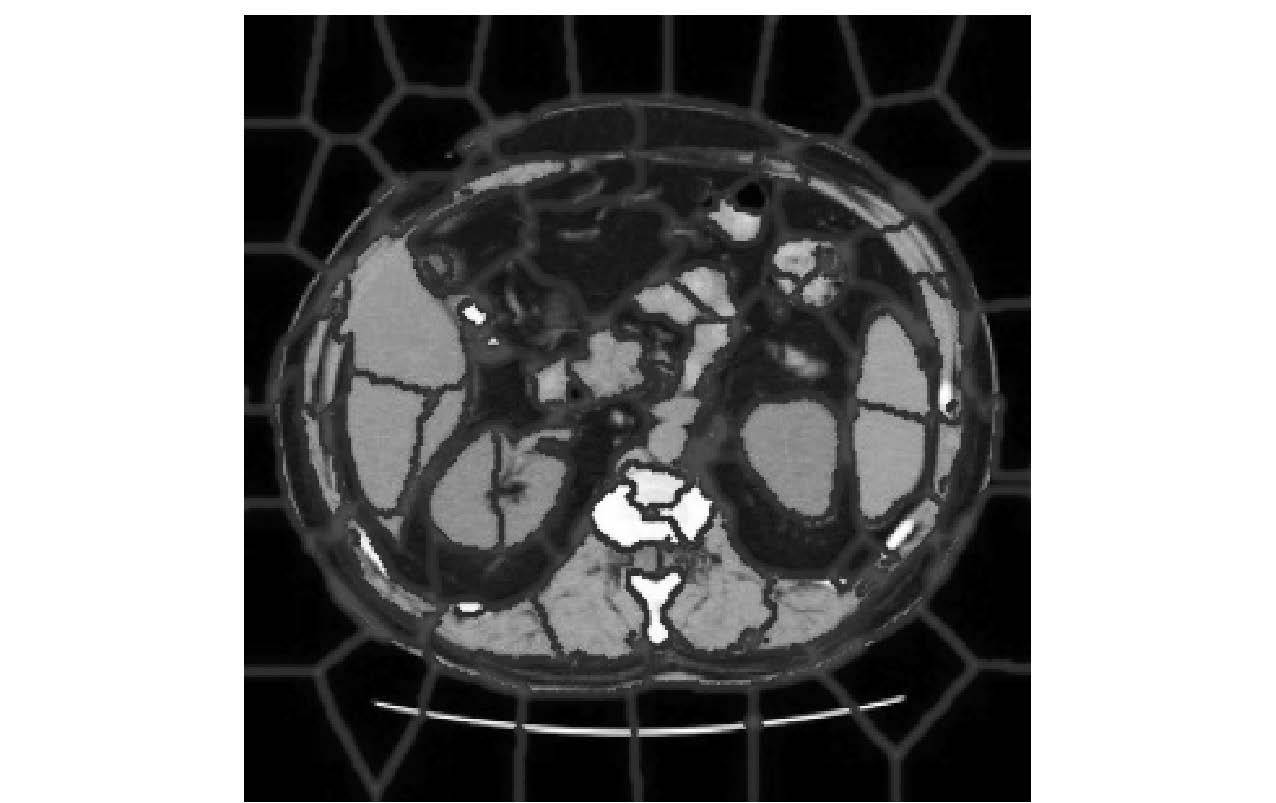
3.1 可视块的生成和单目标分割生成可视块的算法执行结果如图 4所示. 观察可知,利用邻近度、相似度作为标准生成的可视块,较好地聚类了像素点,分割结果较符合人观察所形成的感知.
|
图 4 可视块分割 |
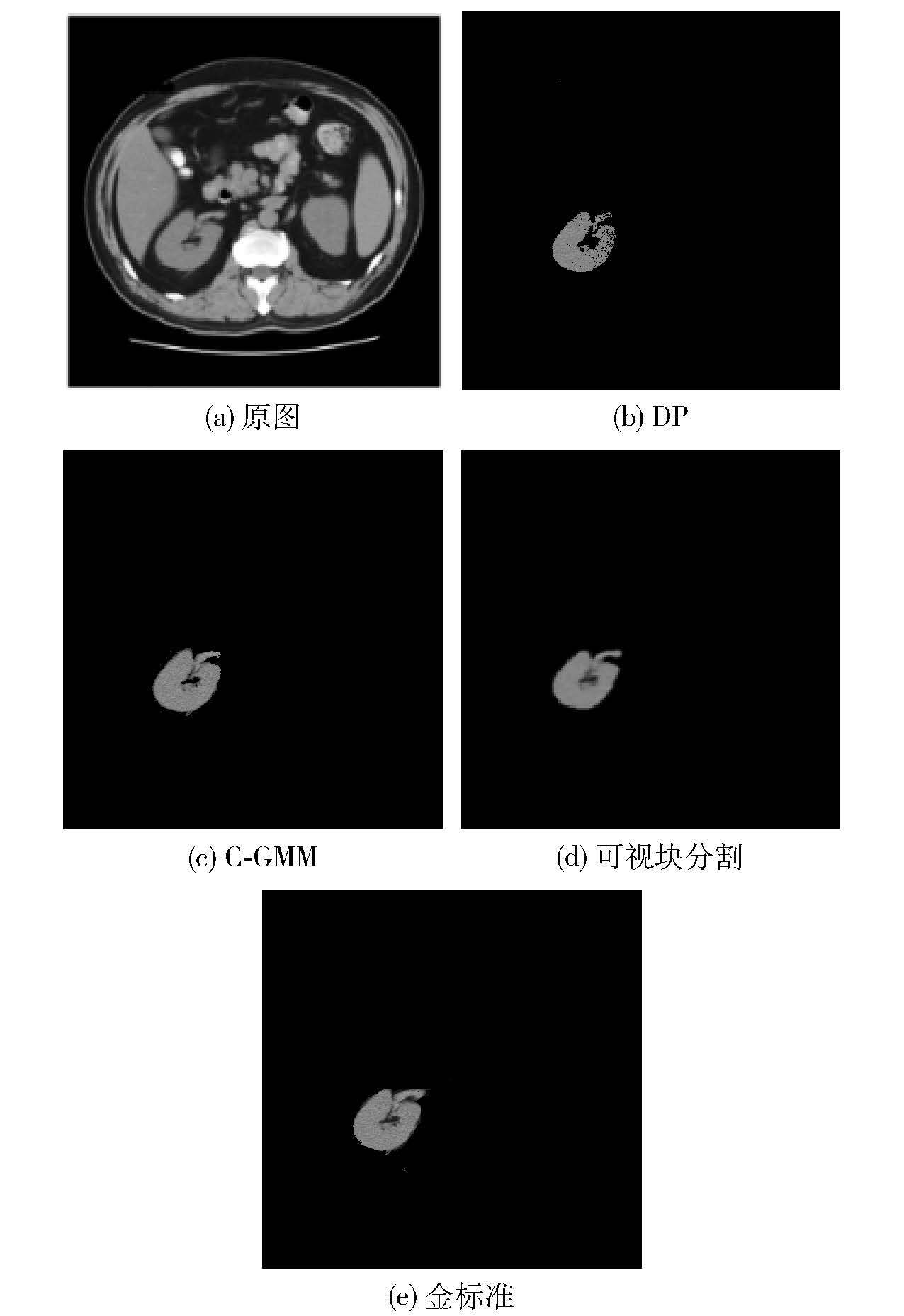
基于可视块,首先验证其分割单目标的能力. 以分割右肾为例,实验结果如图 5所示.
|
图 5 右肾分割实验结果对比 |
狄利克雷过程(DP,Dirichlet process)混合模型利用马尔可夫链采样技术估计区域数量,通过贝叶斯算法估计样本概率,从而完成分类分割的任务. 该算法依赖样本模型,并忽视了像素空间关系对聚类的影响,容易导致欠分割[8]. 高斯混合模型的特征函数(C-GMMs,characteristic function of Gaussian mixture models)算法在每次迭代聚类时利用高斯混合模型的特征函数进行分割,通过期望最大化(EM,expectation maximization)算法估计GMMs所需参数[9]. 另外,笔者的方法选择了梯度最低点作为初始聚类中心,与传统手动标记的方法对比能明显避免噪声影响. 在聚类过程加入空间关系,能有效抑制过分割、欠分割,还能保持原始图像中所有目标区域的信息. 因此,可视块生成可提供良好的计算机辅助诊断基础.
为了评价可视块理论在医学图像上分割结果的有效性,笔者采用同质性准则,同质性表示的是图像局部区域纹理变化大小,取值范围为[0, 1]. 同质性值越大,表示图像局部纹理的变化越小,也就是说局部纹理越均匀. 图 6为度量图 4的同质性的结果展示. 可以看出,80%以上的可视块的同质性值都大于0.8,即纹理较为均匀;而其余的可视块尽管同质性值较低,但在聚类分割时由于空间邻近度的限制,相邻像素被聚类成块,有力地证明了空间邻近度在可视块分割中的关键作用. 由此可见,可视块的分割理论完全适用于医学图像分割,并得到了较好的分割结果.

|
图 6 同质性评价 |
笔者提出的多目标是指腹部CT影像中的肝、肾、脾、胆囊这4种脏器,算法以可视块为单位分割聚类,参考了图像的灰度、空间距离、相对位置和纹理关系.
在多目标分割实验中,选择了TCIA数据集中20个病人,约为14 000幅腹部CT图像序列作为测试样本. 图 7展示了笔者算法和各对照算法执行多目标分割任务的准确率. 从图 7可以看出,随着腹部CT样本切片数量的不断增加,各个器官的分类分割准确率也随之升高,最后趋于稳定. 由于胆囊所占腹腔体积比例较小,因此一套CT序列切片中出现胆囊的几率较小,即样本数较少. 脾脏与相邻的组织密度比较相似,很难区分. 因此,脾脏比其他几个器官的分割准确率相对也较低.

|
图 7 基于可视块分类的分割准确率 |
为了对比试验分割结果,由式(6)定义分割准确率评价分割效果. 其中,T为分割正确的像素点个数,F为分割错误的像素点个数,A为分割准确率. 表 1说明了笔者提出的分类分割算法相对于传统的分类分割和多目标分割方法,是一种有效的多目标腹部CT图像分割方法.
| $A=\frac{T}{T+F}$ | (7) |
|
|
表 1 不同算法下腹部CT图像器官分割准确率 |
表 1所示为笔者验证试验中所有算法准确率结果对比,其中各项值由式(6)计算求得.
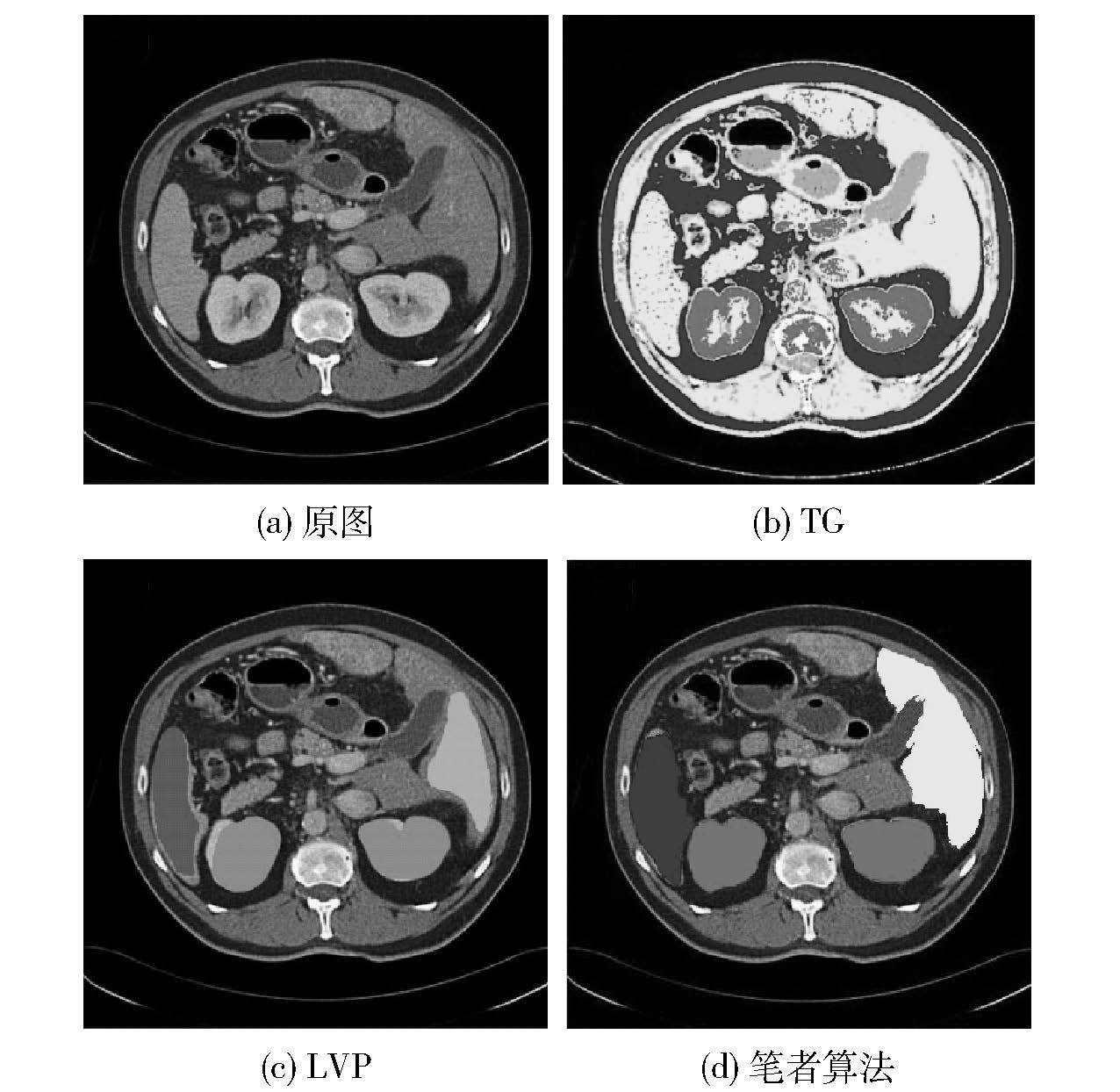
通过对比表 1中数据,在分割准确率的表现方面,可以看出,笔者提出的多目标分割算法效果最好. 图 8为相应算法的分割结果展示.
|
图 8 分割算法的实验结果对比 |
通过分析可知,TG算法利用了全局像素点迭代,使用阈值和梯度方法,不可避免地受到了噪声和灰度不均匀的影响. 此外,该算法以像素的灰度作为分割的唯一特征,忽略了器官之间的相关性,很容易造成过分割现象. 虽然LVP算法考虑到了器官的空间相关性,但却依赖于通过全局像素点的相似性计算. 这种方法对器官多而复杂的腹部分割得到的模型并不完全准确,且个体差异较大的器官和组织也不适用. 笔者提出算法在可视块分割的基础上,降低了人体的各异性,并将器官的底层特征和空间相关性结合起来,是视觉特征和物理特征的融合,通过多分类的原理将多个器官对象分割开来. 综上,在TCIA数据集上的实验和分析,验证了笔者算法的有效性.
4 结束语基于格式塔认知理论,提出了一种结合自底向上聚类和自顶向下分类的可视块分割算法. 笔者算法以腹部器官的纹理、平均灰度为特征,吸收器官之间的空间相关性的先验知识,实现了腹腔CT软组织的多目标分割算法. 算法分为2个步骤,第1步生成可视块,利用结合了相似度、邻近度度量标准Ds聚类可视块,最终生成表现一致的可视块;第2步以可视块为单元,通过结合高层次的相似度、邻近度进一步聚类. 实验结果表明,笔者算法具有更好的分类效率和准确率. 可以肯定的是,基于可视块的多目标分类分割方法不但提高了分割的精度和效率,还具有更一般的适用性.
| [1] | Withey D J, Koles Z J. Medical image segmentation: methods and software[C]//Noninvasive Functional Source Imaging of the Brain and Heart and the International Conference on Functional Biomedical Imaging, 2007. NFSI-ICFBI 2007. Joint Meeting of the 6th International Symposium on. IEEE, 2007: 140-143. |
| [2] | Wolz R, Chu Chengwen, Misawa K, et al. Automated abdominal multi-organ segmentation with subject-specific atlas generation[J]. Medical Imaging, IEEE Transactions on , 2013, 32 (9) :1723–1730. doi:10.1109/TMI.2013.2265805 |
| [3] | Okada T, Linguraru M G, Hori M, et al. Multi-organ segmentation in abdominal CT images[C]//Engineering in Medicine and Biology Society (EMBC), 2012 Annual International Conference of the IEEE. IEEE, 2012: 3986-3989. |
| [4] | Liu Yinxiao, Liang Guoyuan, Saha P K. A new multi-object image thresholding method based on correlation between object class uncertainty and intensity gradient[J]. Medical Physics , 2012, 39 (1) :514–532. doi:10.1118/1.3668058 |
| [5] | Liu Xiaofeng, Linguraru M G, Yao Jianhua, et al. Abdominal multi-organ localization on contrast-enhanced CT based on maximum a posteriori probability and minimum volume overlap[C]//Biomedical Imaging: from Nano to Macro, 2011 IEEE International Symposium on. IEEE, 2011: 2083-2086. |
| [6] | Selver M A, Kocao Ağlu A, Akyar H, et al. Patient oriented neural networks to overcome challenges of abdominal organ segmentation in CT angiography studies[C]//Electrical and Electronics Engineering, 2009. ELECO 2009.[S.l.]: IEEE, 2009: 177-181. |
| [7] | Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on , 2012, 34 (11) :2274–2282. doi:10.1109/TPAMI.2012.120 |
| [8] | Bo Hua, Ma Fulong, Jiao Licheng. Research on computation of GLCM of image texture[J]. Acta Electronica Sinica , 2006, 1 (1) :155–158. |


