为了更好地解决高冲突证据的融合问题,提出一种3条证据直接融合的改进D-S算法.该算法首先根据证据支持贴近度函数给出识别框架下各焦元支持度的计算方法;其次根据三维证据直接融合产生的冲突因子的性质及各焦元的支持度,提出一种基于D-S证据组合规则的冲突信息加权分配算法;最后以多传感器多目标识别系统为背景进行仿真实验.理论分析和仿真结果表明,基于三维证据直接融合的改进D-S算法具有较强的抗干扰性能,能有效融合各种冲突信息,提高目标识别概率.
In order to better solve the fusion problem of high conflict evidence, an improved D-S algorithm fusing three pieces of evidence directly was proposed. Firstly, the calculation method of the support of each focal element under the identification framework is given according to the function of evidence supporting measurement of similarity. Secondly, a weighted assignment algorithm of conflicting information based on D-S evidence combination rule is put forward according to the properties of the conflicting factor generated in the direct fusion process of three-dimensional evidence and the support degree of each focal element. Finally, simulation is implemented under the background of multi-sensor multi-target recognition system. Analysis and simulation show that the improved D-S algorithm based on direct fusion of three-dimensional evidence has a strong anti-interference performance, and it can fuse various types of conflicting information effectively and improve the target recognition probability.
在证据之间存在高度冲突时,利用D-S证据组合规则得到的信息融合结果往往有悖常理[1]. 为解决这一问题,学者们给出了诸多的改进算法[2-5]. 曹洁等[6]提出从分析焦元可信度出发给出局部冲突信息再分配的准则,该算法充分考虑了证据源中各焦元的重要性,提高了融合结果的准确性. Dezert等[7]根据D-S证据理论的局限性提出DSmT证据理论,由于DSmT保留了矛盾焦元,主焦元信度赋值收敛速度较慢,推理相对复杂. 胡丽芳等[8]在DSmT组合规则的基础上,提出将支持证据的冲突信息按照一定的比例在涉及的焦元及其并集间进行分配,加快了算法的收敛速度,也使算法的计算量得以大大减少.
上述改进算法分别在不同程度上提高了目标识别的准确性,但其多是针对两组证据之间的融合规则进行改进. 为提高多源信息的利用率,笔者针对三维(3-D,three-dimensional)证据进行直接融合,并根据3-D冲突信息的结构特点和各焦元被各证据所支持的度量将矛盾信息在相关焦元间进行加权分配.
1 D-S证据组合规则假设有一包含n个穷举和相互排斥焦元的识别框架Θ,即$\Theta =\{{{\theta }_{1}},{{\theta }_{2}},\ldots ,{{\theta }_{n}}\}$. 定义Θ上的基本信度赋值函数$m:{{2}^{\Theta }}\to [0,~1]$,满足条件:$m\left( \varnothing \right)=0\sum\limits_{A\in {{2}^{\Theta }}}{m\left( A \right)=1}0\le m\left( A \right)\le 1$. 这里,m(A)表示对焦元A的信任程度.
定义1 (D-S证据组合规则):如果m1,m2是识别框架Θ上2个相互独立的基本信度赋值函数,其焦元分别为Ai(i=1,2,…,n),则这2个证据共同作用下各焦元的基本信度赋值为
| $m\left( X \right)=\left\{ \begin{align} & 0,X=\varnothing \\ & \frac{\sum\limits_{{{A}_{i}}\in {{2}^{\Theta }},\cap {{A}_{i}}=X}{\prod\limits_{j=1}^{2}{{{m}_{j}}({{A}_{i}})}}}{1-K},X\ne \varnothing \\ \end{align} \right.$ | (1) |
其中$K=\sum\limits_{{{A}_{i}}\in {{2}^{\Theta }},\cap {{A}_{i}}=\varnothing }{\prod\limits_{j=1}^{2}{{{m}_{j}}({{A}_{i}})}}$,称K为不一致因子,1-K为归一化因子.
对于多条证据源的融合,相关研究大多是利用D-S证据组合规则进行两两融合,那么多条证据两两融合与多条证据共同融合在信息融合效果和2种算法的计算复杂度方面有什么区别呢?下面针对该问题进行简单分析.
当有J(J≥2)条证据需要融合时,D-S证据理论组合规则的融合公式为m
| $m\left( X \right)=\left\{ \begin{align} & 0,X=\varnothing \\ & \frac{\sum\limits_{\cap {{A}_{i}}=X}{\prod\limits_{j=1}^{J}{{{m}_{j}}({{A}_{i}})}}}{1-{{K}^{1}}},X\ne \varnothing \\ \end{align} \right.$ | (2) |
其中
| ${{K}^{1}}=\sum\limits_{\cap {{A}_{i}}=\varnothing }{\prod\limits_{j=1}^{J}{{{m}_{j}}({{A}_{i}})}}$ | (3) |
下面以3条证据为例,证明利用式(2)对3条证据进行直接融合与利用式(1)将其进行两两顺序融合所得融合结果是一致的.
假设识别框架U={A,B,C},有以下3组证据:
| ${{m}_{u}}:{{m}_{u}}\left( A \right)\text{ }{{m}_{u}}\left( B \right)\text{ }{{m}_{u}}\left( C \right),u=1,2,3$ |
为方便计算,假设各证据中不知道部分U = 0,并将归一化因子记为S.
1.1 3条证据直接融合根据多组证据组合式(2)可知,3条证据共同融合的一致性因子S可表示为
| $\begin{align} & S={{m}_{1}}\left( A \right){{m}_{2}}\left( A \right){{m}_{3}}\left( A \right)+{{m}_{1}}\left( B \right){{m}_{2}}\left( B \right){{m}_{3}}\left( B \right)+ \\ & {{m}_{1}}\left( C \right){{m}_{2}}\left( C \right){{m}_{3}}\left( C \right) \\ \end{align}$ | (4) |
则3条证据直接融合的结果为
| $m\left( A \right)=({{m}_{1}}\oplus {{m}_{2}}\oplus {{m}_{3}})\left( A \right)=\frac{{{m}_{1}}\left( A \right){{m}_{2}}\left( A \right){{m}_{3}}\left( A \right)}{S}$ | (5) |
| $m\left( B \right)=({{m}_{1}}\oplus {{m}_{2}}\oplus {{m}_{3}})\left( B \right)=\frac{{{m}_{1}}\left( B \right){{m}_{2}}\left( B \right){{m}_{3}}\left( B \right)}{S}$ | (6) |
| $m\left( C \right)=({{m}_{1}}\oplus {{m}_{2}}\oplus {{m}_{3}})\left( C \right)=\frac{{{m}_{1}}\left( C \right){{m}_{2}}\left( C \right){{m}_{3}}\left( C \right)}{S}$ | (7) |
首先,对于前2条证据,其一致性因子为
| ${{S}_{12}}={{m}_{1}}\left( A \right){{m}_{2}}\left( A \right)+{{m}_{1}}\left( B \right){{m}_{2}}\left( B \right)+{{m}_{1}}\left( C \right){{m}_{2}}\left( C \right)$ | (8) |
两两融合后的结果为
| ${{m}_{12}}\left( A \right)=({{m}_{1}}\oplus {{m}_{2}})\left( A \right)=\frac{{{m}_{1}}\left( A \right){{m}_{2}}\left( A \right)}{{{S}_{12}}}$ | (9) |
同理可得m12(B)和m12(C).
将前2条证据融合后的结果作为一条新证据与第3条证据利用式(1)进行两两融合,其一致性因子为
| $\begin{align} & {{S}_{123}}=\frac{{{m}_{1}}\left( A \right){{m}_{2}}\left( A \right){{m}_{3}}\left( A \right)}{{{S}_{12}}}+\frac{{{m}_{1}}\left( B \right){{m}_{2}}\left( B \right){{m}_{3}}\left( B \right)}{{{S}_{12}}}+ \\ & \frac{{{m}_{1}}\left( C \right){{m}_{2}}\left( C \right){{m}_{3}}\left( C \right)}{{{S}_{12}}}=\frac{S}{{{S}_{12}}~} \\ \end{align}$ | (10) |
融合结果为
| $\begin{align} & {{m}_{123}}\left( A \right)=({{m}_{12}}\oplus {{m}_{3}})\left( A \right)=\frac{{{m}_{1}}\left( A \right){{m}_{2}}\left( A \right){{m}_{3}}\left( A \right)/{{S}_{12}}}{{{S}_{123}}}= \\ & \frac{{{m}_{1}}\left( A \right){{m}_{2}}\left( A \right){{m}_{3}}\left( A \right)}{S} \\ \end{align}$ | (11) |
同理可得m123(B)和m123(C).
比较式(5)和式(11)可知,根据D-S证据组合规则,将3条证据进行直接融合和将其进行两两融合所得融合结果一致. 该结论不难推广到多条证据的情形.
3条证据共同融合没能改善证据融合效果. 其原因是在利用式(2)对3条证据进行直接融合时,形如(A,A,B)或者(B,B,C)结构的大量冲突信息,均被视为矛盾信息平分掉了,未加以充分利用. 为此,笔者考虑将K1中形如(A,A,B)的矛盾信息根据A、B两焦元被各证据支持程度的大小加权分配给相应焦元,以提高高冲突情况下矛盾信息的利用率.
2 3-D改进D-S算法为了计算各焦元被多条证据支持的度量,引入证据支持贴近度函数[3].
定义2 设J条证据源R1,R2,…,RJ在相同的识别框架Θ下相应的信度赋值分别为m1,m2,…,mJ,在Shafer模型下存在一个正定矩阵D,矩阵中的元素是由D(A,B)=|A∩B|/|A∪B|来确定,其中A,B∈2Θ,则2个证据源之间的证据支持贴近度函数定义为
| $\begin{align} & {{N}_{J}}({{m}_{{{j}_{1}}}},{{m}_{{{j}_{2}}}})=1-\frac{1}{\sqrt{2}}{{({{({{m}_{{{j}_{1}}}}-{{m}_{{{j}_{2}}}})}^{\text{T}}}D({{m}_{{{j}_{1}}}}-{{m}_{{{j}_{2}}}}))}^{1/2}}, \\ & \forall {{j}_{1}},{{j}_{2}}=1,2,\ldots ,J;\text{ }{{j}_{1}}\ne {{j}_{2}}~ \\ \end{align}$ | (12) |
定义3 对于定义2中的J条证据,其中一条证据被其他证据支持的程度可表示为
| $\sup {{~}_{{{j}_{1}}}}=\prod\limits_{{{j}_{2}}=1}^{J}{{{N}_{J}}({{m}_{{{j}_{1}}}},{{m}_{{{j}_{2}}}})},\forall {{j}_{1}},{{j}_{2}}=1,2,\cdots ,J$ | (13) |
将式(13)进行归一化,可得
| $\text{cre}{{\text{d}}_{{{j}_{1}}}}=\frac{\sup {{~}_{{{j}_{1}}}}}{\sum\limits_{{{j}_{1}}=1}^{J}{\sup {{~}_{{{j}_{1}}}}}},{{j}_{1}}=1,2,\cdots ,J$ | (14) |
定义4 对于定义2中的J条证据,焦元Ai被所有证据支持的度量总和为
| $\lambda ({{A}_{i}})=\sum\limits_{{{j}_{1}}=1}^{J}{\text{cred}{{~}_{{{j}_{1}}}}}m({{A}_{{{j}_{1}}}})\forall i=1,2,\cdots ,n$ | (15) |
根据上述定义,将形如(Ap,Ap,Aq)的冲突信息分配为
| $\omega ({{A}_{p}})=\frac{\lambda ({{A}_{p}})({{m}_{{{j}_{1}}}}({{A}_{p}})+{{m}_{{{j}_{2}}}}({{A}_{p}}))}{\lambda ({{A}_{p}})({{m}_{{{j}_{1}}}}({{A}_{p}})+{{m}_{{{j}_{2}}}}({{A}_{p}}))+\lambda ({{A}_{q}}){{m}_{{{j}_{3}}}}({{A}_{q}})}$ | (16) |
| $\omega ({{A}_{q}})=\frac{\lambda ({{A}_{q}}){{m}_{{{j}_{3}}}}({{A}_{q}})}{\lambda ({{A}_{p}})({{m}_{{{j}_{1}}}}({{A}_{p}})+{{m}_{{{j}_{2}}}}({{A}_{p}}))+\lambda ({{A}_{q}}){{m}_{{{j}_{3}}}}\left( {{A}_{q}} \right)}$ | (17) |
其中:$\forall p,q=1,2,\cdots ,n,p\ne q;\forall {{j}_{1}},{{j}_{2}},{{j}_{3}},{{j}_{1}}\ne {{j}_{2}}\ne {{j}_{3}}$.则基于3-D信息直接融合的D-S改进组合规则可以描述为
| $m\left( X \right)=\left\{ \begin{align} & 0,X=\varnothing \\ & \frac{\sum\limits_{\cap {{A}_{i}}=X}{\prod\limits_{j=1}^{3}{{{m}_{j}}({{A}_{i}})}}+\sum \omega \left( X \right)\eta }{1-{{K}^{2}}},X\ne \varnothing \\ \end{align} \right.$ | (18) |
其中
| $\begin{align} & \eta =\sum\limits_{{{A}_{r}}\cap {{A}_{h}}=\varnothing }{{{m}_{{{j}_{1}}}}({{A}_{r}}){{m}_{{{j}_{2}}}}({{A}_{r}}){{m}_{{{j}_{3}}}}({{A}_{h}})}, \\ & \forall {{j}_{1}},{{j}_{2}},{{j}_{3}}=1,2,3{{j}_{1}}\ne {{j}_{2}}\ne {{j}_{3}}\forall r,h=1,2,\cdots ,n \\ & {{K}^{2}}=\sum\limits_{{{A}_{{{i}_{1}}}}\cap {{A}_{{{i}_{2}}}}\cap {{A}_{{{i}_{3}}}}=\varnothing }{{{m}_{{{j}_{1}}}}({{A}_{{{i}_{1}}}}){{m}_{{{j}_{2}}}}({{A}_{{{i}_{2}}}}){{m}_{{{j}_{3}}}}({{A}_{{{i}_{3}}}})}, \\ & \forall {{i}_{1}},{{i}_{2}},{{i}_{3}}=1,2,\cdots ,n;\text{ }{{i}_{1}}\ne {{i}_{2}}\ne {{i}_{3}}; \\ & \forall {{j}_{1}},{{j}_{2}},{{j}_{3}}=1,2,\cdots ,J;\text{ }{{j}_{1}}\ne {{j}_{2}}\ne {{j}_{3}} \\ \end{align}$ | (19) |
与式(3)相比,式(19)要求${{A}_{{{i}_{1}}}}\cap {{A}_{{{i}_{2}}}}\cap {{A}_{{{i}_{3}}}}=\varnothing $中i1≠i2≠i3,即在3-D改进D-S算法中,不一致因子仅包含形如(A,B,C)的冲突信息,即改进算法将含有丰富目标信息的冲突信息在相关焦元上进行了加权分配,避免了经典D-S算法在处理高冲突证据时,由于有效信息量不足导致融合结果出错或组合规则失效的不足.
3 仿真及分析为验证所提改进算法的有效性,以多传感器多目标识别系统为背景进行仿真分析. 现假设有4部传感器对某一区域中3个未知目标进行观测识别,识别框架Θ={A,B,C},其中A为驱逐舰,B、C均为普通货船,4条证据的基本信度赋值为
| $\begin{align} & {{m}_{1}}\left( A \right)={{x}_{1}},{{m}_{1}}\left( B \right)={{x}_{2}},{{m}_{1}}\left( C \right)=1-{{x}_{1}}-{{x}_{2}}; \\ & {{m}_{v}}\left( A \right)={{y}_{1}},{{m}_{v}}\left( B \right)={{y}_{2}},{{m}_{v}}\left( C \right)=1-{{y}_{1}}0{{y}_{2}}; \\ & \forall {{x}_{1}},{{x}_{2}}\in [0,~1];\forall {{y}_{1}},{{y}_{2}}\in [0,~1];v=2,3,4 \\ \end{align}$ |
3个目标A、B、C均在与传感器识别系统相距100 km处相对均匀航行,舰船的相对速度均为1 000 m/s. 传感器1正确判断3个目标的舰船种类的置信度始终分别为x1、x2、1-x1-x2,传感器2、3、4在100 km处对目标A舰型的置信度均为0.43,在10 km处对A舰型进行准确识别的可能性均为0.7,在此期间对A舰型的识别准确程度与其实时距离成反比;在整个过程中,除干扰阶段外,传感器2、3、4正确判断B船类型的置信度始终为0.1. 在2舰船相距30~20 km处,传感器3受到干扰,正确判断A、B两船类型的可能性为0.
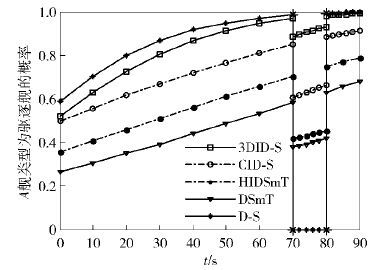
图 1和图 2分别给出了在探测环境相对较好和探测环境比较恶劣2种情况下,所提3-D改进D-S(3DID-S)算法、 D-S算法、基于证据加权融合的改进D-S(CID-S)算法[6]、 DSmT算法和改进DSmT(HIDSmT)算法[8]正确判断A舰舰型概率的比较.
|
图 1 x1=0.7,x2=0.05 |
|
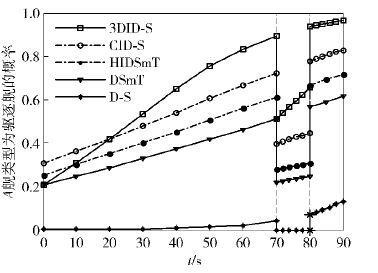
图 2 x1=0.001,x2=0.499 |
由图 1和图 2可以看出,在多传感器系统探测环境比较好且各证据没有发生高度冲突的情况下,D-S算法的证据融合效果明显比其他4种算法都要好,其他4种算法中,以所提3DID-S算法效果最好. 而在探测环境变差或受到干扰时,D-S组合规则中不一致因子接近于1或等于1,D-S证据组合算法效果变差甚至失效. 这时3DID-S算法和CID-S算法识别效果较好,而DSmT算法和HIDSmT算法的识别效果不及上述2种算法. 原因是由于3DID-S算法充分利用了3-D冲突信息中的有用信息,减少了信息的不确定性;CID-S算法不仅考虑了证据源的可信度,还考虑了不同证据源中的同一焦元在冲突信息再分配中的权重,因此,尽管采用的是两两融合算法,其信息的有效利用率相对较高;DSmT由于保留了矛盾焦元,收敛速度较慢;HIDSmT算法将支持证据的冲突信息按照一定的比例在涉及的焦元及其并集间分配,使主焦元的收敛速度加快,但该算法没考虑证据源之间的关联程度,影响了信息的利用效果.
4 结束语探讨了一种基于3-D证据直接融合的D-S改进算法,该算法将有2个测量来源于同一目标的三元冲突信息在涉及的焦元间根据其被证据支持的程度进行合理分配. 实验结果表明,即使在多传感器系统探测能力非常差的情况下,所提改进算法也能快速识别出目标,表现出较强的抗干扰性能. 因此,所提基于改进D-S证据组合规则的目标识别算法是一种能较好融合高冲突信息的目标识别算法.
| [1] | Dezert J, Smarandache F. Advances and applications of DSmT for information fusion (Vol 3)[M]. Rehoboth: American Research Press , 2009 . |
| [2] | 韩德强, 杨艺, 韩崇昭. DS证据理论研究进展及相关问题探讨[J]. 控制与决策 , 2014, 29 (1) :1–11. Han Deqiang, Yang Yi, Han Chongzhao. Advances in DS evidence theory and related discussions[J]. Control and Decision , 2014, 29 (1) :1–11. |
| [3] | 李新德. 多源不完善信息融合方法及其应用研究[D]. 武汉: 华中科技大学, 2007. Li Xinde. Research on fusion method of imperfect information from multi-source and its application[D]. Wuhan: Huazhong University of Science and Technology, 2007. |
| [4] | 江涛. 基于D-S证据理论的信息融合算法[J]. 计算机科学 , 2013, 40 (11) :120–124. Jiang Tao. Information fusion algorithm based on D-S evidence theory[J]. Computer Science , 2013, 40 (11) :120–124. |
| [5] | Duanmu Dejie, Jiang Wen, Fan Xin, et al. A novel weighted combination method of conflicting evidences[J]. ICIC Express Letters , 2013, 7 (2) :499–504. |
| [6] | 曹洁, 郭雷雷. 一种基于局部冲突分配的证据组合规则[J]. 计算机应用研究 , 2013, 30 (7) :2033–2035. Cao Jie, Guo Leilei. Evidence combination rule based on local conflict distribution strategy[J]. Application Research of Computers , 2013, 30 (7) :2033–2035. |
| [7] | Dezert J, Smarandache F. Advances and application of DSmT for information fusion (Vol 1)[M]. Rehoboth: American Research Press , 2004 . |
| [8] | 胡丽芳, 关欣, 何友. 一种新的基于DSmT的合成公式[J]. 火力与指挥控制 , 2009, 34 (7) :9–11. Hu Lifang, Guan Xin, He You. A new combination rule based on DSmT[J]. Fire Control and Command Control , 2009, 34 (7) :9–11. |


