针对货车滚动轴承轨边声学诊断中高速移动带来的声信号频移和频带扩展问题,提出一种基于到达时差和时域插值的多普勒畸变信号矫正方法.通过对轴承运动特性与故障特征频率分析,建立轨边传声器阵列的布放准则,在此基础上通过对阵列检测声信号进行分帧加窗和互相关分析,计算传声器间时延差;引入到达时差技术实时估计故障轴承的移动位置和传播时延,通过时域插值,获得以移动轴承发声时间序列为基准的无时延接收声信号.仿真结果表明,该方法在低信噪比时仍可有效矫正多普勒畸变的声信号,且适用于定转速及变转速场合.
For problems of frequency shift and bandwidth extension of high-speed movement in wayside wheel-bearing acoustic diagnosis, a Doppler effect removal method was proposed based on time difference of arrival and time-domain interpolation. Based on the defect of characteristic frequencies and moving characters of bearings, the placement rules of the trackside microphone array was designed. Through framing, windowing and cross-correlation, the time delay differences among microphones are calculated. The time difference of arrival technique was introduced to estimate the moving position and propagation delay of fault bearings in real time. Through the time domain interpolation, the acoustic signal is received without extension based on the time series of moving bearings. Simulation demonstrates that the algorithm can remove the Doppler effect of acoustic signal effectively in low signal to noise ratio. It is suitable for both constant and variable speed.
滚动轴承是铁路货车走行部中最重要的机械零件之一,由于长期高速重载运行而极易发生表面剥离等故障,导致切轴、脱轨等恶性事故,造成重大经济损失,因此对其实施在线故障检测至关重要. 声学诊断技术具有非接触测量、可对移动目标在线监测、传声器安装灵活等优点,是一种较为有效的诊断方法. 实际应用中,轴承高速移动导致传声器接收声信号产生多普勒畸变,出现频移与频带扩展等现象,造成虚警或误诊断.
针对信号的多普勒畸变问题,Stojanovic等[1]提出用锁相环技术进行多普勒相位补偿,并运用在潜水器与水面舰艇声呐通信中;随后,Sharif等[2]将相关分析技术用于传输信号的多普勒估计. 但是,上述方法主要解决通信级别信号畸变问题,并不适用于轨边轴承声信号多普勒矫正. 近年来,国内外一些学者开展了有针对性的相关研究,初步取得了一些研究成果. 例如,2012年吴强等[3]引入重采样技术矫正多普勒畸变信号,该方法主要适用于低转速场合. 随后,Hu等[4]提出一种基于时频脊线提取和重采样技术的多普勒矫正方法,但是,在背景噪声较强时存在时频脊线难以提取的问题. 针对高速移动和强噪声场合,Liu等[5]改进了基于瞬时频率的重采样技术,提出参数自动估计方法,建立一种自适应多普勒矫正策略,该方法在最优参数选取过程中需要对多个未知参数进行遍历和相似度匹配,计算量较大.
笔者提出一种基于到达时差(TDOA,time difference of arrival)和时域插值的检测声信号多普勒效应矫正方法. 通过对轴承运动特性和故障特征频率的综合分析,建立轨边传声器阵列的布放准则,给出接收信号的时间模型,在此基础上对阵列检测声信号进行分帧加窗和互相关分析,获取移动轴承的实时位置和传播时延,结合以移动轴承发声时间序列为参考基准的收声传感器的时间序列,矫正阵列检测传感器的多普勒畸变信号.
1 轨边阵列传声器布放准则货车在高速运动和强背景噪声下,单个传声器采集的声信号可能具有不完整性、不确定性(仅是一个周期的片段信息),因此,考虑采用线型传声器阵列检测方式,通过多传声器检测信号融合,以获得故障轴承完整周期的声信号. 传声器阵列布置需要综合考虑阵列的高度、距离轨道的垂直距离以及阵列长度等.
为了获取高信噪比的故障声信号,阵列传声器采用指向性安装方式,直接朝向货车轴承的中心. 阵列长度则应满足大于等于轴承最大故障周期内货车运行距离,以获得任意故障类轴承的完整周期信号. 下面对传声器阵列长度公式进行推导.
假设货车运行速度V和单个故障周期内行车距离E分别为
| $V=n\pi {{D}_{\text{w}}}~$ | (1a) |
| $E=V/{{f}_{\text{e}}}~$ | (1b) |
其中:n为转速,Dw为车轮直径,fe为轴承的故障特征频率,具体计算公式可参照文献[6]. 则外圈、内圈、滚子和保持架的单故障周期内货车运行距离可分别表示为
| ${{E}_{\text{ORE}}}=\frac{-2\pi {{D}_{\text{w}}}D}{N(d\cos ~\alpha -D)}$ | (2a) |
| ${{E}_{\text{IRE}}}=\frac{2\pi {{D}_{\text{w}}}D}{N(d\cos ~\alpha +D)}\text{ }$ | (2b) |
| ${{E}_{\text{BF}}}=\frac{-2\pi d{{D}_{\text{w}}}D}{{{d}^{2}}\cos ~{{\alpha }^{2}}-{{D}^{2}}}$ | (2c) |
| ${{E}_{\text{CF}}}=\frac{-2\pi d{{D}_{\text{w}}}D}{d\cos ~\alpha -D}$ | (2d) |
其中N、d、D和α分别为轴承的滚子数、内径、节径和滚子接触角. 可见,单故障周期内货车运行距离与转速无关,可根据轴承尺寸和车轮直径信息计算所需阵列长度.
下面以常用的SKF197726货车滚动轴承为例,计算轨边阵列的长度. d=0.023 8 m,D=0.18 m,α=10°,N=20,Dw=0.8 m,计算可得EORF=0.29 m,EIRF=0.22 m,EBF=0.676 m,ECF=5.8 m. 为了能够获取不同种类故障的完整周期声信号,则阵列接收声信号的有效范围至少为ECF. 考虑到背景噪声以及声信号在空气中衰减等因素,单个传声器接收轴承声信号的有效范围并非无限远,当车速运行在40~60 km/h时,实测范围约为1.5 m,则至少需要4个传声器组成线型传声器阵列,实时拾取运行货车轴承声信号.
引入TDOA和时域插值技术,设计给出一种高速移动下阵列检测声信号的多普勒效应去除算法,主要包括接收信号时间模型、故障轴承实时定位和时域插值矫正.
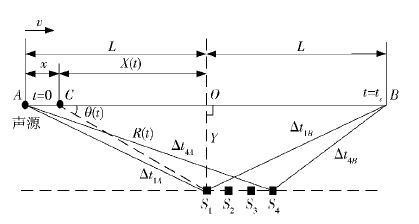
1.1 接收信号时间模型参照货车滚动轴承轨边声学诊断中阵列传声器的布放准则,假设货车沿轨道(AB)以速度v运行,可得阵列接收轴承声信号的时间模型,如图 1所示. 其中,圆点表示声源,方块表示传声器,Si(i=1,2,3,4)表示接收传声器.
|
图 1 阵列接收信号的时间模型 |
设S1与轨道垂直相交于O点,距离为Y. 货车运动到起始点A的时刻为零点,到达终止点B的时刻为tB,总运行距离为2L,O为AB的中点. 声源从A、B传播到S1、S4的时延分别为Δt1A、Δt4A、Δt1B、Δt4B.
各接收传声器信号组成如图 2所示,可表示为

|
图 2 传声器信号组成时间 |
| ${{S}_{i}}=\left\{ \begin{align} & {{a}_{i}}+{{b}_{i}},i=1 \\ & {{a}_{i}}+{{b}_{i}}+{{c}_{i}},i=2,3,4~ \\ \end{align} \right.$ | (3) |
其中:bi为接收有效轴承声信号的时间片段,ai、ci为无轴承声信号的时间片段. 由于终止点B位于阵列的右侧,显然Δt1B>ΔtiB(i≠1),即各传声器的接收时长并非相等.
1.2 故障轴承实时定位基于传声器的接收信号时间模型,引入互相关与TDOA方法实时定位移动轴承的位置,以获得传声器与轴承间的时延. 具体计算步骤如下.
第1步 计算时延差. 由于相邻传声器采集的声信号存在一定程度的重叠或者说均采集到了故障声信号片段,可通过分帧、加窗和互相关分析,当相关函数取最大值时,计算得到二者时延差. 对于有限长的信号a(n)和b(n),互相关函数计算方法为
| ${{r}_{ab}}\left( m \right)=\frac{1}{N}\sum\limits_{N=0}^{N-1}{a\left( n \right)b\left( n+m \right)~}$ | (4) |
其中:N为a(n)、b(n)数据点数的一半,m为0~N-1.
需要说明的是,考虑到各传声器接收信号时长不相等,在进行互相关分析前,以1号传声器为基准,采用补零方式将各传声器信号转化成等时长.
第2步 依据传声器阵列几何位置关系和所得时延差,实时估计故障轴承的位置. 在货车运动过程中,因滚动轴承距离地面高度一定、轴承与传声器阵列间垂直距离已知,且轴承沿直线运动,则声源定位问题就可简化为二维平面上直线运动轨迹计算.
假设传声器及故障轴承坐标分别为$({{x}_{i}},{{y}_{i}})\left( x,y \right)$,声源到传声器i与j之间距离差${{r}_{i,j}}={{r}_{i}}-{{r}_{j}}$,其中ri为声源到传声器i的距离,由位置关系有
| $r_{i}^{2}={{({{r}_{i,j}}+{{r}_{j}})}^{2}}={{({{x}_{i}}-x)}^{2}}+{{({{y}_{i}}-y)}^{2}}$ | (5) |
设i=1、j=2,将已知条件y=b代入,化简可得
| ${{x}^{2}}+\frac{(x_{2}^{3}-{{x}_{2}}r_{1,2}^{2})}{(r_{1,2}^{2}-x_{2}^{2})}x+\frac{4r_{1,2}^{2}(x_{2}^{2}+{{b}^{2}})-{{(x_{2}^{2}+r_{1,2}^{2})}^{2}}}{4(r_{1,2}^{2}-{{x}^{2}}_{2})}=0$ | (6) |
该二项式的解即为声源位置.
1.3 时域插值矫正轴承运动过程中,传声器的接收时延不断变化. 依据滚动轴承的实时位置信息,采用改进的时域插值方法,将接收声信号还原为无时延或等时延,矫正多普勒畸变信号.
以S1接收信号矫正过程为例,如图 1所示,轴承声信号为m(t),在某时刻t (0≤t
| $\Delta t=\sqrt{{{\left( L-x \right)}^{2}}+{{Y}^{2}}/c}$ | (7) |
其中c为声速.
传声器的接收时间为${{t}_{\text{r}}}=t+\Delta t$,采用三次样条插值对接收信号进行插值采样,得到幅值K. 需要说明的是,插值过程中会出现接收时间的最大值大于接收信号的总时长,若直接根据外推法去估计会产生较大误差,为此,采取减小插值序列长度或增加收声序列长度的方法来解决,使得$\max ({{t}_{\text{r}}})\le \Delta {{t}_{1B}}+{{t}_{B}}$. 最后,由发声时间t(n)与插值幅值序列K(n)组成离散序列即为多普勒矫正后时域信号.
综上所述,算法整体流程概括如下:
1) 对阵列传声器检测声信号进行分帧加窗和互相关计算,实时估计滚动轴承的位置;
2) 假设采样频率f,发声的时间序列即为t$t\left( n \right)=\left\{ 0,1/f,2/f,\ldots ,\left( N-1 \right)/f \right\}$,依据传播距离序列$R\left( n \right)=\left\{ 0,{{R}_{1}},{{R}_{2}},\ldots ,{{R}_{N-1}} \right\}$,可得移动轴承的传播时延序列$\Delta t\left( n \right)=\{0,\Delta {{t}_{1}},\Delta {{t}_{2}},\ldots ,\Delta {{t}_{N-1}}\}$;
3) 依据传播时延,计算收声时间序列${{t}_{\text{r}}}\left( n \right)=t\left( n \right)+\Delta t\left( n \right)$,以此对收声信号进行插值得到幅值序列K(n),即为以t(n)为参考时间的矫正信号.
2 仿真验证仿真参数具体设置如下:轴承故障频率f1=100Hz,发声信号$m\left( t \right)=\sin (2\pi {{f}_{1}}t)$,L=7m,初速度v=30 m/s,加速度a=20m/s2,阵列传声器数n=4,采样率f=40 kHz,发声时间序列t={0,1/f,2/f,…,(N-1)/f},轴承起始点到各传声器的垂直距离为[7 8.5 10 11.5],铁轨与阵列垂直距离Y=2m. 在互相关分析时,帧长w=40 ms,帧移p=0.2w,窗函数为Hamming窗.
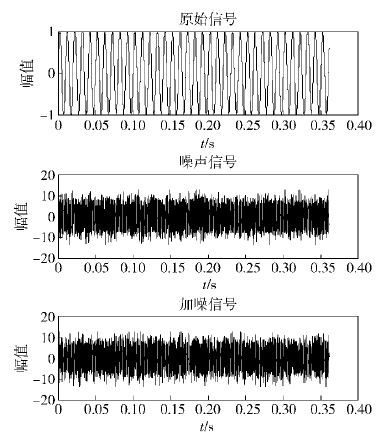
当货车高速运行(如60~100 km/h)时,存在风噪以及轮轨撞击等复杂的背景噪声,受实验条件限制,难以采集到真实的背景噪声,因此通过在轴承故障仿真信号中加入高斯白噪来模拟,信噪比为-20 dB. 轴承故障、噪声及混合信号的时域波形如图 3所示,可以看出,原始轴承故障信号完全淹没在背景噪声中.
|
图 3 轴承故障、噪声及混合信号的时域波形 |
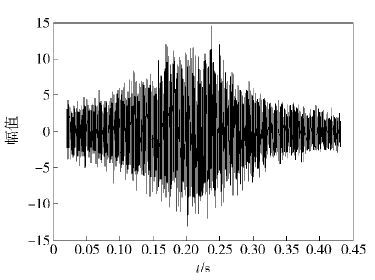
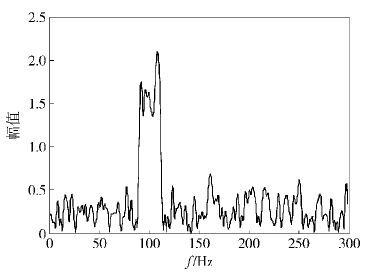
距离声源起始位置最近端的传声器所接收的原始声信号及矫正前频谱曲线分别如图 4、图 5所示. 可以看出,随着轴承向检测传声器移动,时域信号的幅值逐渐增大,频域曲线在以100 Hz为中心点附近出现了明显的展宽现象.
|
图 4 传声器接收的原始信号 |
|
图 5 矫正前频谱曲线 |
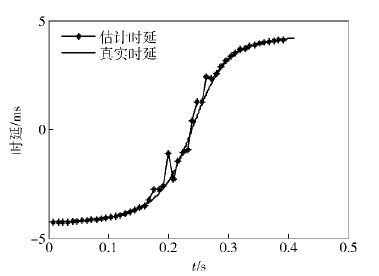
通过互相关计算和TDOA分析,可得阵列传声器的时延差及滚动轴承位置曲线,如图 6、图 7所示.
|
图 6 时延差曲线 |
|
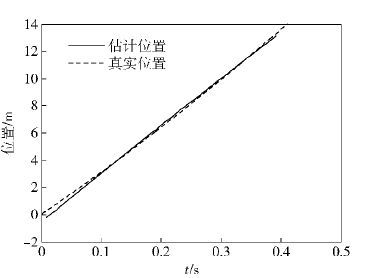
图 7 轴承位置估计 |
1) 传声器1、3间时延差的估计值与理论值在[0 s,0.18 s]与[0.25 s,0.4 s] 时间段内吻合度较高,但是在 (0.18 s,0.25 s)的吻合度较低,出现了比较大的波动. 原因有两方面,一是随着声源与传声器间相对位置的改变,受多普勒效应的影响,传声器间接收信号的相似度存在较大差异,尤其在两接收传声器中垂线与运动轨迹交点处,导致互相关的计算时延精度较低. 对于运动轨迹不在声源与传声器连线上的情况,多普勒频移f′与源信号频率fs的关系为$f\prime ={{f}_{s}}\frac{1}{1-M\cos \alpha }$,其中M为马赫数,α为声源、传声器连线与声源运动轨迹间夹角. 可知,当声源与阵列距离较远时,声源与各传声器的α角之间差异较小,f′差异几乎为零,此时各传声器接收信号相似,基于互相关的时延计算精度较高. 当声源运行在传声器阵列中间时,声源与两接收传声器的α角之间差异较大,f′差异变大,此时,一个接收信号频率压缩. 另外一个原因是频率展宽,导致信号间存在本质差异,难以通过互相关准确计算时延差,产生如图 6所示的时延剧烈波动现象. 二是低信噪比情况下,广义互相关准确度受到影响,增大了时延估计误差. 针对上述问题,采用对位置曲线二阶拟合的方法减小误差.
2) 拟合后轴承移动位置曲线与理论值曲线基本重合,在初始以及终止时刻误差相对较大(约5%),原因在于轴承位置估计过程中,尽管图 6显示时延偏差在首尾部分要小于中间区域,但是,算法的估计精度在不同位置受时延误差的影响程度不同,在相同误差下,位置偏差随着轴承远离检测传声器而增大,因此,在起始时刻尽管时延差较小,但却造成较大的位移估计误差.
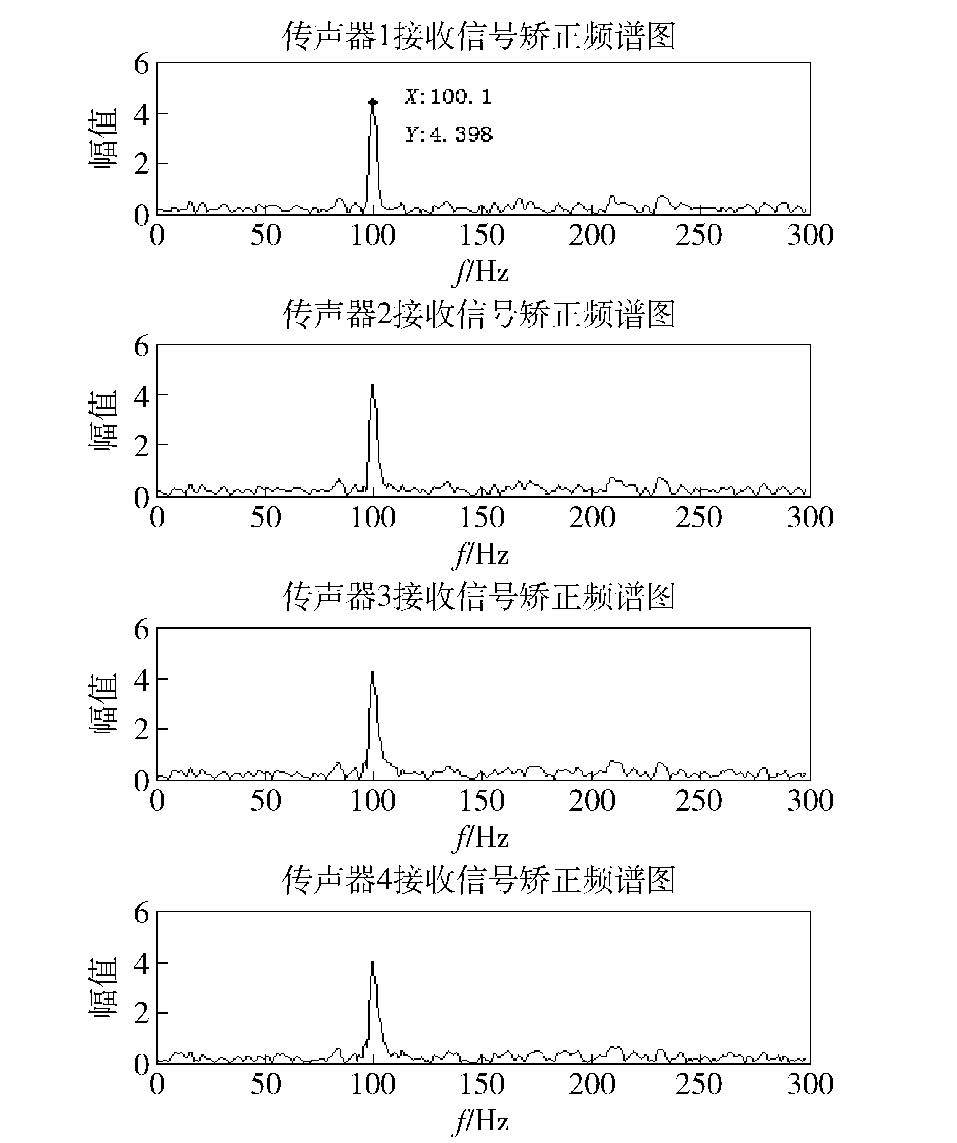
依据时延差以及轴承位置信息,采用时域插值对检测声信号进行矫正,结果如图 8所示. 可以看出,各传声器的接收信号频率展宽现象明显消失,仅在100 Hz处有较强能量,幅值远大于噪声幅值. 这说明,所提出算法能够有效去除检测声信号的多普勒畸变问题,并且该方法可适用于变转速情形.
|
图 8 矫正后信号的频谱曲线 |
给出了适用于货车轴承轨边声学检测的传声器阵列部署准则,在此基础上提出一种基于TDOA和时域插值的多普勒矫正算法. 该方法不仅可以准确估计出传声器间时延差以及轴承实时位置,而且能够在较低信噪比的情况下有效去除检测声信号的多普勒畸变现象,凸显轴承的故障特征频率,对于促进轴承故障诊断技术的发展具有重要理论意义.目前主要基于仿真信号验证算法有效性,下一步将对实测信号加以验证并进行算法改进设计.
| [1] | Stojanovic M, Catipovie J A, Proakis J G. Phase-coherent digital communications for underwater acoustic channels[J]. Oceanic Engineering , 1994, 19 (1) :100–111. doi:10.1109/48.289455 |
| [2] | Sharif B S, Neasham J, Hinton O R, et al. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering , 2000, 25 (1) :52–61. doi:10.1109/48.820736 |
| [3] | 吴强, 孔凡让, 何清波, 等. 基于重采样技术的声学信号多普勒畸变矫正[J]. 信号处理 , 2012, 28 (9) :1308–1313. Wu Qiang, Kong Fanrang, He Qingbo, et al. Doppler shift correction for acoustic signals using resampling technique[J]. Signal Processing , 2012, 28 (9) :1308–1313. |
| [4] | Hu Fei, Shen Changqing, Liu Fang, et al. Doppler shift elimination methods based on instantaneous frequency estimation for the wayside acoustic signal[J]. Applied Mechanics and Materials , 2013, 333-335 :510–515. doi:10.4028/www.scientific.net/AMM.333-335 |
| [5] | Liu Fang, He Qingbo, Kong Fanrang, et al. Doppler effect reduction based on time-domain interpolation resampling for wayside acoustic defective bearing detector system[J]. Mechanical Systems and Signal Processing , 2014, 26 (2) :253–271. |
| [6] | Chen Bin, Yan Zhaoli, Chen Wei. Defect detection for wheel-bearings with time-spectral kurtosis and entropy[J]. Entropy , 2014, 16 (1) :607–626. doi:10.3390/e16010607 |


