2. 西安交通大学 电子与信息工程学院, 西安 710054
针对l1范数下奇异值分解的l1-SVD稀疏信号重建的波达方向估计方法存在求解量的稀疏性较差且空间谱中存在较多的伪峰,不能准确估计波达方向的问题,对接收信号矩阵进行预处理,并使用信号子空间设计权值矢量得到更好的稀疏性和更好地逼近l0范数,利用得到的权值矢量对l1-SVD算法中解矢量的各个元素进行加权,以得到的加权l1范数作为最小化的目标函数进行优化.仿真结果表明,提出的算法在快拍数、正则化参数和信噪比等条件改变的情况下能有效抑制伪峰,并准确稳定地估计出波达方向.
2. The School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710054, China
When l1-SVD algorithm is used for direction of arrival (DoA) estimation with few snapshots and low signal noise ratio (SNR), there appear pseudo peaks in spatial spectrum, which lead to inaccurately DoA estimation results. To deal with this problem, the article proposes a DoA estimation method based on sparse signal recovery utilizing weighted 1 norm. Based on the sparse recovery, the weight vector is chosen from the signal subspace and received signal matrix is multiplied. Then the product between weights and elements in the result is made to get weighted 1 norm is taken as target function for minimization. Simulations demonstrate that the proposed algorithm could effectively restrain the pseudo peak and accurately estimate the DoA under the different snapshots, regularization parameter and SNR.
波达方向(DoA,direction of arrival)估计一直以来都是阵列信号处理领域的研究热点,诸多的算法,如极大似然[1-2](ML,maximum likehood)、多重信号分类[3](MUSIC,multiple signal classification)、旋转不变子空间[4](ESPRIT,estimation of signal parameters via rotational invariance techniques)等被提出来. 以上算法在实际应用中需要解决一些特殊问题,如算法的鲁棒性、实时性和实现复杂度等. 如多重信号分类算法通过特征值分解(EVD,eigen value decomposition)或奇异值分解(SVD,singular value decomposition)计算信号子空间或噪声子空间,求解时存在谱峰搜索过程,这些过程涉及的运算量巨大.
近些年,基于稀疏信号重构的新型方法相继出现[5-8],用稀疏信号表示框架下的DoA估计算法不同于子空间类算法,不需要事先知道信源个数,不要求信号源独立,不管相干信源或非相干信源均能处理,且对阵列误差敏感度低. Fuchs[5]提出利用全局匹配滤波器白化稀疏协方差矩阵的模型来估计波达方向,增加了计算复杂度. Malioutov等[6]提出基于奇异值分解的稀疏重构估计DoA方法免去谱峰搜索的烦琐过程,但在低快拍数、低信噪比和正则化参数改变的情况下,会出现伪峰和估计不准确的问题. Zheng等[7]提出用噪声子空间来设计权值矢量,韩树楠等[8]提出用信号傅里叶变换后的空间谱来设计权值矢量,但两者都面临在低快拍数、低信噪比情况下如何选择合适的正则化参数保证算法稳定的问题.
为了解决在低快拍数、低信噪比和正则化参数改变的情况下,l1-SVD算法出现伪峰和估计不准确的问题,笔者提出稀疏信号重建的新方法,基于l1范数在时域对信号模型进行稀疏重构,将原本的DoA估计问题转化为稀疏信号重构的问题,用信号模型的协方差函数对接收信号矩阵进行预处理,利用信号子空间设计加权矢量,用得到的权值矢量对l1-SVD算法中解矢量的各个元素进行加权,以得到的加权l1范数作为最小化的目标函数进行优化,从而实现DoA估计. 计算时通过二阶锥规划问题[9]实现DoA估计. 仿真结果证明,在低快拍数和低信噪比下算法能有效抑制伪峰和在正则化参数改变时算法的稳定性.
1 稀疏信号模型假设K个远场窄带信号入射到M(M>K)个阵元的均匀线阵(ULA,uniform linear array)上,阵元间距为半个波长,每个信号sk(t)来自功率为σk2的不同方向θk,输出M×1信号矢量为
| $x\left( t \right)=\sum\limits_{k=1}^{K}{a({{\theta }_{k}}){{s}_{k}}\left( t \right)+n\left( t \right)}=A\left( \theta \right)s\left( t \right)+n\left( t \right)$ | (1) |
其中:$a({{\theta }_{k}})={{[1,\cdots ,{{e}^{-j2\pi \left( M-1 \right)dsin~\left( {{\theta }_{k}} \right)/\lambda }}]}^{\text{T}}}$,$A\left[ \left( \theta \right)=a({{\theta }_{1}}),\ldots ,a({{\theta }_{k}}) \right]$,$s\left( t \right)={{\left[ {{s}_{1}}\left( t \right),\ldots ,{{s}_{K}}\left( t \right) \right]}^{\text{T}}}$,n(t)为M×1维的矩阵,噪声功率为σn2. 假设输入的s(t)和n(t)都为零均值广义平稳随机信号,且信号的噪声之间不相关. 由式(1)获得M×M的协方差矩阵为
| ${{R}_{x}}=E\{x\left( t \right){{x}^{\text{H}}}\left( t \right)\}=A\left( \theta \right){{R}_{S}}{{A}^{\text{H}}}\left( \theta \right)+\sigma _{n}^{2}{{I}_{M}}$ | (2) |
| ${{R}_{s}}=E\{s\left( t \right){{s}^{\text{H}}}\left( t \right)\}=\text{diag}(\sigma _{1}^{2},\ldots ,\sigma _{K}^{2})$ | (3) |
其中:(·)*,(·)T,(·)H,(·)-1,E(·)分别为矩阵的共轭、转置、共轭转置、求逆和求均值.
为了在实际应用中更好地确定信源位置,利用稀疏信号表示的形式处理信号,稀疏信号模型表示为
| $X=BS+N$ | (4) |
其中:$X=[x({{t}_{1}}),\cdots ,x({{t}_{L}})\left] B= \right[{{b}_{1}},\cdots ,{{b}_{{\bar{K}}}}]$,bi为对应角度θi的方向矢量,$\Theta =\{{{{\bar{\theta }}}_{1}},\cdots ,{{{\bar{\theta }}}_{{\bar{K}}}}\}$为空间域中所有可能角度的范围,S$S=[\bar{s}({{t}_{1}}),\cdots ,\bar{s}({{t}_{L}})\left] N= \right[n({{t}_{1}}),\cdots ,n({{t}_{L}})],\bar{K}\gg M>K.\text{ }B$是由所有可能角度的范围决定,并不需要知道实际信号,这就意味着只要找到s(tl)中的非零元素也就估计出了信号方向. 此时DoA估计问题就转化为式(4)中的稀疏重构问题.
2 信号子空间加权l1范数法稀疏信号重构l1-SVD算法[6]中快拍数为K的信号模型为
| ${{X}_{\text{SV}}}=B{{S}_{\text{SV}}}+{{N}_{\text{SV}}}$ | (5) |
其中:XSV、SSV、NSV分别为减小快拍数后的输出信号、输入信号和噪声.
为了让求解量达到更好的稀疏性,对式(5)中的信号矩阵矢量进行预处理,令${{X}_{\text{SVW}}}=R_{x}^{-1/2}{{X}_{\text{SV}}}{{B}_{\text{w}}}=R_{x}^{-1/2}B,{{R}_{x}}$为原信号矢量的协方差矩阵. 此时式(7)中的问题变为
| $\min ~\frac{\|{{X}_{\text{SVW}}}{{B}_{\text{w}}}{{S}_{\text{SV}}}\|_{2}^{2}}{2}+\lambda \|{{s}^{({{l}_{2}})}}{{\|}_{1}}~$ | (6) |
但是,在多数情况下,s(l2)并不满足s(l2)≤1,这就意味着l1范数并不是l0范数的凸包络. 因此式(10)没有达到较好规划的效果. 在低信噪比情况下,l1-SVD算法结果的稀疏性难以保证,因此对解矢量s(l2)各个元素进行加权处理,得到加权的l1范数,以此来促进解矢量的稀疏性,抑制伪峰,得到更好的效果.
具体做法是对原信号模型的协方差矩阵Rx进行特征值分解(EVD,eigen value decomposition),其中大特征值对应的特征向量组成信号子空间为Us,小特征值对应的特征向量组成噪声子空间为Un,根据文献[6],利用信号子空间设计的权值为
| ${{\omega }_{i}}=\sqrt{\frac{b_{i}^{\text{H}}{{U}_{\text{s}}}U_{\text{s}}^{\text{H}}{{b}_{i}}}{LK}}$ | (7) |
其中涵盖所需方向最大的信息,此时有不等式为
| $s_{i}^{{{l}_{2}}}\le \frac{LK}{b_{i}^{\text{H}}{{U}_{\text{s}}}U_{\text{s}}^{\text{H}}{{b}_{i}}}$ | (8) |
这时如果sil2中的矢量元素来自实际信号,那么${{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}$趋近于1,否则趋近于0. 这时在处理实际问题时可将其转化为优化问题为
| $\min ~\frac{\|{{X}_{\text{SVW}}}-{{B}_{\text{w}}}{{S}_{\text{SV}}}\|_{2}^{2}}{2}+\lambda \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}}$ | (9) |
用二阶锥规划问题表示为
| $\left. \begin{align} & ~\min p+\lambda q \\ & \text{s}.\text{t}.~\frac{\|{{X}_{\text{SV}}}-B{{S}_{\text{SV}}}{{\|}_{2}}}{2}\le p \\ & \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}} \\ \end{align} \right\}$ | (10) |
通过用子空间设计权值处理问题后再对以上二阶锥规划问题[9]进行操作就可达到算法的要求. 利用CVX优化工具包[10]来处理式(10)中的最优化问题.
3 正则化参数正则化参数λ对性能的影响是很重要的,如果λ的值取太大,那么在l1形式下有可能造成错误的波达方向估计,如果λ的值取太小,那么在l1形式下会有伪峰出现. 所以需要根据理论指导来正确选择λ[11]. 将式(13)向量化,得到
| $\begin{align} & \underset{s}{\mathop{\min }}\,\frac{\|y\|_{2}^{2}}{2}+\lambda \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}} \\ & \text{s}.\text{t}.y={{{\bar{x}}}_{\text{w}}}-{{{\bar{B}}}_{\text{w}}} \\ \end{align}$ | (11) |
其中:${{{\bar{x}}}_{\text{w}}}$,s分别为对XSVW和SSV的矢量化,Bw=blkdiag{Bw,…,Bw}为MK×KK维的块对角化矩阵. 写成拉格朗日双重标准式为
| $\underset{s,y}{\mathop{\min }}\,~\frac{\|y\|_{2}^{2}}{2}+\lambda \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}}+{{\mu }^{\text{T}}}(y-{{{\bar{x}}}_{\text{w}}}+{{{\bar{B}}}_{\text{w}}}s)$ | (12) |
首先最小化y,当y=-μ时达到最小,此时式(16)变为
| $\underset{s,y}{\mathop{\min }}\,~-\frac{\|\mu \|_{2}^{2}}{2}-{{\mu }^{\text{T}}}{{{\bar{x}}}_{\text{w}}}+\lambda \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}}+{{\mu }^{\text{T}}}{{{\bar{B}}}_{\text{w}}}s$ | (13) |
然后最小化s,这时相当于最小化$\lambda \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}}+{{\mu }^{\text{T}}}{{{\bar{B}}}_{\text{w}}}s$,有
| $\lambda \sum\limits_{i=1}^{{\bar{K}}}{{{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}}+{{\mu }^{\text{T}}}{{{\bar{B}}}_{\text{w}}}s=\sum\limits_{i=1}^{{\bar{K}}}{(\lambda {{\omega }_{i}}s_{i}^{\left( {{l}_{2}} \right)}+\bar{\beta }_{i}^{\text{T}}{{s}_{i}})_{i}^{\left( {{l}_{2}} \right)}}$ | (14) |
这时等号右边等式达到最小即可,也就是si=0时等号右边函数达到最小,这时式(15)可写为
| $\begin{align} & \underset{\mu }{\mathop{\min }}\,\frac{\|\mu \|_{2}^{2}}{2}+{{\mu }^{\text{T}}}{{{\bar{x}}}_{\text{w}}} \\ & \text{s}.\text{t}.~\|{{{\bar{\beta }}}_{i}}{{\|}_{2}}\le \lambda {{\omega }_{i}},i=1,\ldots ,\bar{K} \\ \end{align}$ | (15) |
选择的正则化参数满足$\sum\limits_{j=1}^{K}{{{(\bar{b}_{ij}^{\text{T}}({{{\bar{x}}}_{\text{w}}}-{{{\bar{B}}}_{\text{w}}}s))}^{2}}}\le \lambda \min ~\left\{ W \right\},i=1,\ldots ,\bar{K}W={{[{{\omega }_{1}},\ldots ,{{\omega }_{{\bar{K}}}}]}^{\text{T}}}$即可.
4 仿真结果及分析仿真结果对笔者提出的算法和经典的Capon算法[12]、MUSIC算法[3]和l1-SVD算法[8]在不同快拍数、不同信噪比和正则化参数改变时分别进行比较. 实验中2个远场窄带非相干信号从20°,30°方向上入射到8个阵元的均匀线阵上,阵元间距为半波长. 角度变化范围为-90°~90°,间隔为1°.
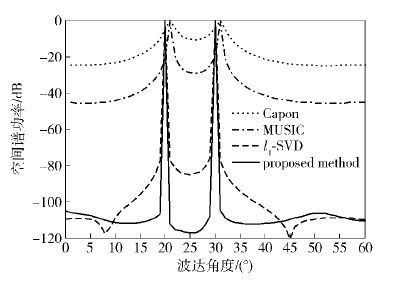
实验1对传统经典的DoA估计算法、l1-SVD算法和提出的加权l1-SVD算法在不同快拍数下进行对比. 其中信噪比为20 dB,正则化参数为2,快拍数分别为200和50,如图 1和图 2所示.
|
图 1 快拍数为200的加权l1-SVD算法 |
|
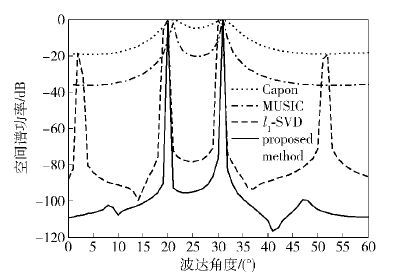
图 2 快拍数为50的加权l1-SVD算法 |
由图 1和图 2可以看出,在快拍数变少的情况下,l1-SVD算法出现伪峰,提出的加权l1-SVD算法能有效抑制伪峰的出现,得到更好的DoA估计结果.
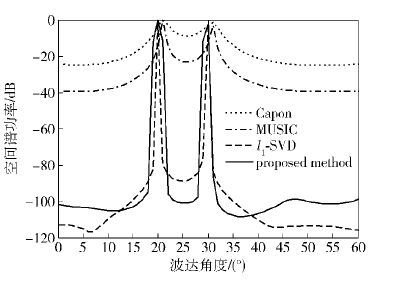
实验2验证了加权l1-SVD算法在低信噪比下估计DoA的情况,其中快拍数为200,正则参数为2,信噪比分别为20 dB和-20 dB,如图 3和图 4所示.
|
图 3 信噪比SNR=20 dB时的加权l1-SVD算法 |

|
图 4 信噪比SNR=-20 dB时的加权l1-SVD算法 |
由图 3和图 4可以看出,在降低信噪比的情况下,l1-SVD算法出现伪峰,提出的方法能有效抑制伪峰的出现且稳定有效地估计出波达方向.
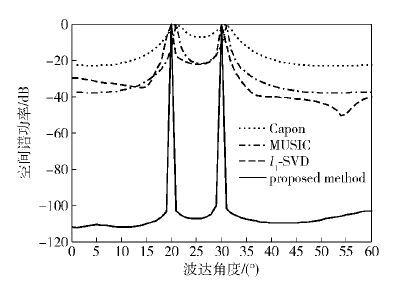
实验3对比实验1和实验2在降低正则化参数下,提出的加权l1-SVD算法估计波达方向的情况,其中快拍数为200,信噪比为20 dB,正则化参数降为1,如图 5所示.
|
图 5 正则化参数为1的加权l1-SVD算法 |
由图 5可以看出,在正则化参数改变的情况下,l1-SVD算法不能准确地估计出DoA,而提出的方法有较好的鲁棒性和稳定性,能有效准确地估计出波达方向,针对正则化参数在稀疏重建的DoA估计方法中有较大影响的情况下,笔者算法有突出的稳定性. 仿真也验证了正则化参数为1时,快拍数降为50,信噪比为-20 dB的情况,且算法性能依然有较好的鲁棒性和稳定性.
5 结束语笔者提出了基于加权1范数稀疏重建的DoA估计方法,通过对接收信号模型矩阵进行预处理和使用信号子空间设计权值矢量后,达到了更好的稀疏性和更好地逼近了l0范数,最后将得到的加权l1范数作为最小化目标函数来进行处理,达到对波达方向的估计. 仿真结果表明,得到权值的过程计算量小,在少快拍数和低信噪比情况下提出的算法对伪峰有良好的抑制,且表现出较好的稳定性和准确性,正则化参数的选取也是非常重要的,在改变正则化参数的情况下,提出的算法在稳定性方面表现突出.
| [1] | Ziskind I, Wax M. Maximum likelihood localization of multiple source by alternating projection[J]. IEEE Transaction on Acoustics, Speech and Signal Processing , 1998, 36 (10) :1533–1560. |
| [2] | Stoica P, Sharman K C. Maximum likelihood methods for direction-of-arrival estimation[J]. IEEE Transactions on Acoustics, Speech and Signal Processing , 1990, 38 (7) :1132–1143. doi:10.1109/29.57542 |
| [3] | Swindlehurst A, Kailath T. A performance analysis of subspace-baced methods in the presence of model errors, part I: the MUSIC algorithm[J]. IEEE Transactions on Signal Processing , 1992, 40 (7) :1758–1774. doi:10.1109/78.143447 |
| [4] | Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech and Signal Processing , 1989, 37 (7) :984–995. doi:10.1109/29.32276 |
| [5] | Fuchs J J. Identification of real sinusoids in noise, the global matched filter approach[J]. 42nd Asilomar Conference Signals, System and Computers, Pacific Grove, CA , 2008 :269–273. |
| [6] | Malioutov D, Cetin M, Willsky A S. A sparce signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing , 2005, 53 (8) :3010–3022. doi:10.1109/TSP.2005.850882 |
| [7] | Zheng Chundi, Li Gang, Zhang Hao, et al. An approach of DoA estimation using subspace weighted l1 minimization[J]. IEEE International Conference on Acoustics, Speech and Signal Processing , 2011 :2856–2859. |
| [8] | 韩树楠, 李东生, 张浩, 等. 基于加权1范数的稀疏重构波达方向估计算法[J]. 探测与控制学报 , 2015, 37 (2) :82–85. Han Shunan, Li Dongsheng, Zhang Hao, et al. A DoA estimation algorithm based on weighted 1 norm through sparse reconstruction[J]. Journal of Detection and Control , 2015, 37 (2) :82–85. |
| [9] | Lobo M, Vandenberghe L, Boyd S, et al. Applications of second-order cone programming[J]. Linear Algebra Application, Special Issue on Linear Algebra on Control, Signals, and Image Processing , 1998 :193–228. |
| [10] | Grant M, Boyd S. CVX: Matlab software for disciplined convex programming[EB/OL]. 2014.[10] http://cvxr.com/cvx.2014. |
| [11] | Xu Xu, Wei Xiaohan, Ye Zhongfu. DoA estimation based on sparse signal recovery utilizing weighted l1-norm penalty[J]. IEEE Signal Processing Letters , 2012, 19 (3) :155–157. doi:10.1109/LSP.2012.2183592 |
| [12] | Rahmat S, Nurul H N, Ahmed O E R, et al. Capon-like DoA estimation algorithm for directional antenna arrays[J]. Loughborough Antenna and Propagation Conference, UK , 2011 :1–4. |


