2. 北京工业大学 电子信息与控制工程, 北京 100124
为了进一步提高超密集无线网络(UDN)性能,提出一种同时考虑收发信机射频损伤的协同波束形成方法.首先,建立了包含射频损伤的UDN协同波束形成模型,并利用凸优化方法求解得到其最优解;然后,针对此最优解的结构特征,结合其在实际系统中难以实现的局限,设计了由信号泄漏噪声比波束形成导向矢量和最优功率分配构成的线性次优波束形成器.仿真结果表明,收发信机射频损伤的协同波束形成器能有效降低干扰,并且可提高UDN的系统容量.
2. College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China
The coordination beamforming scheme with transceiver radio frequency impairments was proposed to improve the performance of ultra-dense wireless network (UDN). Firstly, the coordination beamforming model based on the residual radio frequency impairments is presented, and the convex optimization algorithm is utilized to achieve the optimal solution. Then, considering the limitations of the implementation of the optimal beamformer, the signal leakage noise ratio based the linear suboptimal beamformer is designed by beamforming steering vector and optimal power allocation. Simulations show that the proposed suboptimal beamformer with radio frequency impairments can effectively reduce interference and improve the sum rate of UDN.
未来无线网络中,为了提高频谱资源的空间复用率,需要在宏基站覆盖区域内,高密度地部署各类低功率无线节点,从而形成超密集无线网络(UDN,ultra-dense wireless networks),这是支持移动互联业务量不断增长的关键. 虽然UDN中小区结构的微型化可大幅度提高系统容量,但同时也带来了更为严重的小区间干扰.
考虑到UDN小区半径的减少易于处理协同波束形成存在的如小区间同步和接收端信息反馈等问题,方正等[1]提出了基于空域协同波束形成的干扰消除方法,但该研究中采用了理想信号模型,没有考虑到实际波束形成系统中收发信机射频损伤对UDN性能的影响.
针对收发信机端射频损伤对协同波束形成系统性能的影响问题,Jose等[2]通过研究补偿后残留射频损伤的聚合效应,提出了残留射频损伤的模型. Du等[3]的研究表明残留射频损伤使得高信噪比时点到点系统容量受限. Li等[4]研究了考虑射频损伤时的多小区加权和速率问题. 这些研究主要从单独发送/接收端器件射频损伤或宏小区部署的角度进行分析,而较少同时考虑收发信机射频损伤对密集部署的UDN系统性能的影响,特别是UDN采用协同波束形成来降低小区间干扰的情况.
为了准确地研究协同波束形成的UDN系统性能,笔者考虑到收发信机端存在的射频损伤,提出一种能够提高UDN容量的低复杂度协同波束形成方法,克服了最优波束形成器难以工程实现的局限.
1 系统模型假设UDN中有Kt个基站,每个基站安装Nm幅天线,总发射天线$N=\sum\limits_{m=1}^{{{K}_{\text{t}}}}{{{N}_{m}}}$. 基站覆盖区内有Kr个用户,且每个用户安装单幅天线. 根据用户终端的位置,将其动态划分为需要进行干扰协调的所有用户集${{C}_{m}}\subseteq \{1,2,\ldots ,{{K}_{\text{r}}}\}$和位于小区中心的用户子集${{D}_{m}}\subseteq {{C}_{m}}$.
假设经过补偿和校准后,发送、接收端残留射频损伤分别为Zm(t)和Zk(r),基站对用户k的发送信号sk~CN(0,1),则用户k的接收信号为
| $\begin{align} & {{y}_{k}}=\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}\left( \sum\limits_{n=1}^{{{K}_{\text{r}}}}{{{D}_{mn}}{{w}_{mn}}{{s}_{n}}+Z_{m}^{\left( \text{t} \right)}} \right)}+ \\ & {{n}_{k}}+Z_{k}^{\left( \text{r} \right)} \\ \end{align}$ | (1) |
其中:协同基站对用户k的波束成形矢量为wk=[w1kT…wKtkT]T,wmk为mth基站对kth用户的Nm×1维波束成形矢量;hk=[h1kT…hKtkT]T∈$\mathbb{C}$N×N为用户k的瑞利信道衰落系数,hmk∈$\mathbb{C}$Nm×1;nk~CN(0,σk2)为用户k接收的高斯噪声;矩阵Dk∈$\mathbb{C}$N×N,其元素${{D}_{mk}}=\left\{ \begin{align} & \text{ }{{I}_{{{N}_{m}}}},k\in {{D}_{m}} \\ & {{0}_{{{N}_{m}}}},其他 \\ \end{align} \right.$;矩阵${{C}_{k}}\in {{\mathbb{C}}^{N\times N}}$,其元素${{C}_{mk}}=\left\{ \begin{align} & \text{ }{{I}_{{{N}_{m}}}},k\in {{D}_{m}} \\ & {{0}_{{{N}_{m}}}},其他 \\ \end{align} \right..$
收发信机的射频损伤可建模为高斯分布的畸变噪声,其中基站发送端射频损伤为$Z_{m}^{\left( \text{t} \right)}\sim CN(0,\xi _{m}^{\left( \text{t} \right)})\xi _{m}^{\left( \text{t} \right)}=diag(\xi _{m,1}^{\left( \text{t} \right),2},\ldots ,\xi _{m,{{N}_{m}}}^{\left( \text{t} \right),2})\text{ }\xi _{m,j}^{\left( \text{t} \right),2}={{\eta }_{j}}\left( \sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|{{[{{D}_{mn}}{{w}_{mn}}]}_{j,:}}\|_{\text{F}}^{2}} \right)$为基站m端天线j的射频损伤,[·]j,:表示矩阵的第j行,ηj(·)为非负的递增凸函数,表示把基站j发送信号映射到射频损伤的函数. 为便于分析,定义矩阵$T\in {{\mathbb{C}}^{N\times N}}$,其中Tn表示仅第n个对角线元素为非零元素的矩阵,则ξm,j(t),2可表示为$\xi _{m,j}^{\left( \text{t} \right),2}={{\eta }_{j}}\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|{{T}_{j}}{{D}_{mn}}{{w}_{mn}}\|_{\text{F}}^{2}}$.
类似地,接收用户k端的射频损伤Zk(r)~ CN(0,ζk(r)),其中ζk(r)=diag(ζk(r),2),$\zeta _{k}^{\left( \text{t} \right),2}={{\nu }_{k}}\sum\limits_{l=1}^{{{K}_{\text{t}}}}{\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|h_{lk}^{\text{H}}{{C}_{lk}}{{D}_{ln}}{{w}_{ln}}\|_{\text{F}}^{2}}}{{\nu }_{k}}\left( \cdot \right)$为非负递增凸函数,表示把接收端用户k的信号映射为射频损伤的函数.
由上定义可得用户k端的接收信号干扰噪声比(SINR,signal to interference plus noise ratio)为
| ${{I}_{k}}=\frac{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mk}}{{w}_{mk}}} \right|}^{2}}}{\sigma _{k}^{2}+\sum\limits_{i\ne k}{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mi}}{{w}_{mi}}} \right|}^{2}}+Z_{k}^{\left( \text{t,r} \right)}}}$ | (2) |
其中Zk(t,r)为收发信机射频损伤的功率,且$Z_{k}^{\left( \text{t,r} \right)}=\zeta _{k}^{\left( \text{r} \right),2}+\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}\xi _{m}^{\left( \text{t} \right)}C_{mk}^{\text{H}}{{h}_{mk}}}$.
在考虑收发信机射频损伤的情况下,UDN协同波束形成可描述为如下单调优化问题:
| $\begin{align} & \underset{{{w}_{1}},\ldots ,{{w}_{{{K}_{\text{r}}}}}}{\mathop{\max }}\,~f({{g}_{1}}({{I}_{1}}),\ldots ,{{g}_{{{K}_{\text{r}}}}}({{I}_{{{K}_{\text{r}}}}})) \\ & s.t.~\text{tr}(\xi _{m}^{\left( \text{t} \right)})+\sum\limits_{k\in {{D}_{m}}}{\|{{w}_{mk}}{{\|}^{2}}}\le {{P}_{\text{tot}}}/\left| A \right| \\ & {{I}_{k}}=\frac{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{w}_{mk}}} \right|}^{2}}}{\sigma _{k}^{2}+\sum\limits_{i\ne k}{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mi}}{{w}_{mi}}} \right|}^{2}}+Z_{k}^{\left( \text{t,r} \right)}}} \\ \end{align}$ | (3) |
其中:gk(Ik)为以SINR为变量的连续、可微、严格单调递增函数,系统效用函数f(g1(I1),…,gKr(IKr))是以gk(Ik)为变量的严格单调递增函数,A为参与协同波束形成的基站集合,每个协同波束形成的基站发射功率和发送端射频损伤功率满足Pm+tr(ξm(t))≤Ptot/|A|,$\forall $m∈A,Ptot为所有协同波束形成基站的总发送功率.
2 协同波束形成器若已知用户的业务质量需求,即固定用户SINR值,则可把收发信机射频损伤的UDN空域协同波束形成模型式(3)转化为凸优化问题而获得全局最优解,即
| $\begin{align} & \text{find}~{{w}_{1}},\ldots ,{{w}_{{{K}_{\text{r}}}}} \\ & \text{s}.\text{t}.\text{tr}(\xi _{m}^{\left( \text{t} \right)})+\sum\limits_{k\in {{D}_{m}}}{\|{{w}_{mk}}{{\|}^{2}}}\le {{P}_{\text{tot}}}/\left| A \right| \\ & {{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{w}_{mk}}} \right|}^{2}}\ge g_{k}^{-1}\left( r_{k}^{*} \right)\times \\ & \left( \sigma _{k}^{2}+\sum\limits_{i\ne k}{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mi}}{{w}_{mi}}} \right|}^{2}}+Z_{k}^{\left( \text{t,r} \right)}} \right) \\ \end{align}$ | (4) |
其中rk*表示用户k的最佳性能rk*=gk(Ik),r1*≥0,…,rKr*≥0.
引入误差向量幅度(EVM,error vector magnitude)来描述发送端射频损伤$\xi _{m,j}^{\left( \text{t} \right),2}={{\eta }_{j}}\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|{{[{{D}_{mn}}{{w}_{mn}}]}_{j,:}}\|_{\text{F}}^{2}}$和收发信机射频损伤$Z_{k}^{\left( \text{t,r} \right)}=\zeta _{k}^{\left( \text{r} \right),2}+\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}\xi _{m}^{\left( \text{t} \right)}C_{mk}^{\text{H}}{{h}_{mk}}}$. 收发信机端射频损伤的EVM分别为
| $E_{j}^{\left( \text{t} \right)}=\frac{{{\eta }_{j}}\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|{{[{{D}_{mn}}{{w}_{mn}}]}_{j,:}}\|_{\text{F}}^{2}}}{\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|{{[{{D}_{mn}}{{w}_{mn}}]}_{j,:}}\|_{\text{F}}^{2}}}$ | (5) |
| $E_{k}^{\left( \text{r} \right)}=\frac{{{\nu }_{k}}\left( \sum\limits_{l=1}^{{{K}_{\text{t}}}}{\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|h_{lk}^{\text{H}}{{C}_{lk}}{{D}_{ln}}{{w}_{ln}}\|_{\text{F}}^{2}}} \right)}{\sum\limits_{l=1}^{{{K}_{\text{t}}}}{\sum\limits_{n=1}^{{{K}_{\text{r}}}}{\|h_{lk}^{\text{H}}{{C}_{lk}}{{D}_{ln}}{{w}_{ln}}\|_{\text{F}}^{2}}}}$ | (6) |
假设EVM为定值,则收发信机射频损伤可表示为线性函数${{\eta }_{j}}\left( x \right)={{a}_{j}}x$(aj为线性函数的常量因子)和νk(x)=bkx(bk为线性函数的常量因子),利用该函数可得式(4)的拉格朗日对偶问题为
| $\begin{align} & \underset{{{\lambda }_{k}}\forall k,{{\mu }_{l}}\forall l}{\mathop{\max }}\,\text{ }\sum\limits_{k=1}^{{{K}_{\text{r}}}}{{{\lambda }_{k}}}-\sum\limits_{m=1}^{{{K}_{\text{t}}}}{{{\mu }_{m}}} \\ & \text{s}.\text{t}.\text{ }{{\mu }_{m}}\ge 0,{{\lambda }_{k}}\ge 0\text{ }\forall k,m, \\ & \underset{{{{\bar{w}}}_{mk}}}{\mathop{\max }}\,\frac{\frac{{{\lambda }_{k}}}{\sigma _{k}^{2}}\bar{w}_{mk}^{\text{H}}h_{mk}^{\text{H}}{{D}_{mk}}\left( \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{D}_{mk}}{{w}_{mk}}} \right){{w}_{mk}}}{\bar{w}_{mk}^{\text{H}}\left( \varphi -\frac{{{\lambda }_{k}}}{\sigma _{k}^{2}}h_{mk}^{\text{H}}{{D}_{mk}}\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{D}_{mk}}{{w}_{mk}}} \right){{{\bar{w}}}_{mk}}}~\text{=} \\ & g_{k}^{-1}(r_{k}^{*}) \\ \end{align}$ | (7) |
其中
| $\begin{align} & \varphi =\frac{{{\mu }_{m}}\left| A \right|}{{{P}_{\text{tot}}}}\left( 1+\sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}D_{mk}^{\text{H}}{{T}_{j}}} \right){{w}_{mk}}+ \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{{{\lambda }_{k}}}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}{{w}_{mk}}}+ \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{{{\lambda }_{k}}}{\sigma _{i}^{2}}b_{k}^{2}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}D_{mk}^{\text{H}}C_{mi}^{\text{H}}{{h}_{mi}}{{w}_{mk}}+ \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{{{\lambda }_{k}}}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}\left( \sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{T}_{j}}{{D}_{mk}}D_{mk}^{\text{H}}} \right)C_{mi}^{\text{H}}{{h}_{mi}}{{w}_{mk}} \\ \end{align}$ |
根据拉格朗日对偶问题的卡罗需-库恩-塔克(KKT,Karush-Kuhn-Tucker)条件求解得到式(7)的最优波束形成矢量wmk及其对偶矢量为
| $w_{mk}^{*}=\sqrt{{{p}_{mk}}}~{{{\bar{v}}}_{mk}}$ | (8) |
其中:$~{{{\bar{v}}}_{mk}}=\frac{\Psi _{mk}^{\dagger }h_{mk}^{\text{H}}{{D}_{mk}}}{\left\| \Psi _{mk}^{\dagger }h_{mk}^{\text{H}}{{D}_{mk}} \right\|}$为基站m对用户k的归一化发送波束形成导向矢量,pmk为基站m分配给用户k的功率,其中
| $\begin{align} & {{\Psi }_{mk}}=\left( \frac{{{\mu }_{m}}\left| A \right|}{{{P}_{\text{tot}}}}\left( 1+\sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{D}_{mk}}D_{mk}^{\text{H}}{{T}_{j}}} \right)~+ \right. \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{{{\lambda }_{k}}}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}}+ \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{{{\lambda }_{k}}}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}\left( \sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{T}_{j}}{{D}_{mk}}D_{mk}^{\text{H}}{{T}_{j}}} \right)C_{mi}^{\text{H}}{{h}_{mi}}+ \\ & {{\left. \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{{{\lambda }_{k}}}{\sigma _{i}^{2}}b_{k}^{2}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}D_{mk}^{\text{H}}C_{mi}^{\text{H}}{{h}_{mi}} \right)}^{\dagger }}h_{mk}^{\text{H}}{{D}_{mk}} \\ \end{align}$ |
由于收发信机射频损伤的最优波束形成器存在拉格朗日因子λ,但通常难以找到一组最优λ参数实现最优波束形成. 因此,基于协同波束形成最优解式(8)的结构特征,下面采用线性次优波束形成导向矢量vmk和最优功率分配pmk来设计UDN协同波束形成器,以此逼近最优系统容量.
考虑到多用户波束形成系统中,基于信号泄漏噪声比(SLNR,signal-to-leakage noise ratio)的线性波束形成器在不同信噪比条件下均具有较好性能,故采用SLNR发送波束形成. UDN系统中用户k的SLNR定义为
| ${{L}_{k}}=\frac{\frac{1}{\sigma _{k}^{2}}{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mk}}{{{\bar{v}}}_{mk}}} \right|}^{2}}~}{\frac{1}{{{\eta }_{mk}}}+\sum\limits_{i\ne k}{\frac{1}{\sigma _{i}^{2}}}{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}{{{\bar{v}}}_{mk}}} \right|}^{2}}\frac{1}{\sigma _{k}^{2}}+Z_{k}^{\left( \text{t,r} \right)}}$ | (9) |
其中参数{ηj}j=1Kt为用户k的接收功率,且${{\eta }_{k}}=\frac{{{P}_{\text{tot}}}}{\left| A \right|\left| {{D}_{m}} \right|},\left| {{D}_{m}} \right|$为服务于用户k的协同基站m包含的用户数.
下面根据式(9)求解次优波束形成导向矢量. 令$a=D_{mk}^{\text{H}}C_{mk}^{\text{H}}{{h}_{mk}}\text{ }A=A\frac{1}{\sigma _{k}^{2}}\sum\limits_{m=1}^{{{K}_{\text{t}}}}{{{\left| h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mk}}{{{\bar{v}}}_{mk}} \right|}^{2}}}$,构建优化问题为
| $\begin{align} & \underset{{{{\bar{v}}}_{mk}}}{\mathop{\min }}\,~~\bar{v}_{mk}^{\text{H}}\frac{\left| .A \right||{{D}_{m}}|}{{{P}_{\text{tot}}}}{{{\bar{v}}}_{mk}}+A+ \\ & \sum\limits_{i\ne k}{\frac{1}{\sigma _{i}^{2}}}\sum\limits_{m=1}^{{{K}_{\text{t}}}}{{{\left| h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}{{{\bar{v}}}_{mk}} \right|}^{2}}}+\frac{1}{\sigma _{k}^{2}}Z_{k}^{\left( \text{t,r} \right)} \\ & \text{s}.\text{t}.\text{ }\bar{v}_{mk}^{\text{H}}a=1\text{ }\forall k,m \\ \end{align}$ | (10) |
由KKT条件得
| $\begin{align} & {{{\bar{v}}}_{mk}}=\left( \frac{\left| .A \right||{{D}_{m}}|}{{{P}_{\text{tot}}}}+\sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{1}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}\sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}}+ \right. \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{1}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}\left( \sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{T}_{j}}} \right)D_{mk}^{\text{H}}C_{mi}^{\text{H}}{{h}_{mi}}+ \\ & {{\left. \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{1}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}b_{k}^{2}D_{mk}^{\text{H}}C_{mi}^{\text{H}}{{h}_{mi}} \right)}^{\dagger }}D_{mk}^{\text{H}}{{h}_{m}} \\ \end{align}$ | (11) |
则收发信机射频损伤的SLNR次优波束形成矢量为
| $v_{mk}^{\left( \text{S} \right)}=\frac{{{{\bar{v}}}_{mk}}}{\|{{{\bar{v}}}_{mk}}{{\|}_{2}}~}$ | (12) |
选择加权算术平均的系统效用函数$\sum\limits_{k\in {{D}_{m}}}{{{\alpha }_{k}}{{g}_{k}}({{I}_{k}})}$(αk为加权因子)作为目标函数来求解分配给用户的功率. 由于采用SLNR波束形成器消除了来自其他用户的干扰,这时用户k的接收SINR为${{I}_{k}}\approx {{S}_{k}}=\frac{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mk}}}\sqrt{{{p}_{mk}}}v_{mk}^{\left( L \right)} \right|}^{2}}}{\sigma _{k}^{2}+Z_{k}^{\left( \text{t,r} \right)}}$,故总系统效用函数可写为$\sum\limits_{k\in {{D}_{m}}}{{{\alpha }_{k}}{{g}_{k}}({{S}_{k}})}$,由此构建功率分配的凸优化问题为
| $\begin{align} & \underset{~{{p}_{jk}}\ge 0\forall k\in {{D}_{j}}}{\mathop{\max }}\,\sum\limits_{k\in {{D}_{m}}}{{{\alpha }_{k}}{{g}_{k}}\left( S \right)} \\ & \text{s}.\text{t}.~\text{tr}(\xi _{E}^{\left( \text{t} \right)})+\sum\limits_{k\in {{D}_{m}}}{\|{{w}_{mk}}{{\|}^{2}}\le {{P}_{tot}}/\left| A \right|\forall m} \\ \end{align}$ | (13) |
其中$S=\frac{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mk}}}\sqrt{{{p}_{mk}}}{{{\bar{v}}}_{mk}} \right|}^{2}}}{\sigma _{k}^{2}+Z_{k}^{\left( \text{t,r} \right)}}$.
由凸优化理论知式(13)的拉格朗日函数为
| $\begin{align} & L=-\sum\limits_{k\in {{D}_{m}}}{{{\alpha }_{k}}{{g}_{k}}}\left( \frac{{{\left| \sum\limits_{m=1}^{{{K}_{\text{t}}}}{h_{mk}^{\text{H}}{{C}_{mk}}{{D}_{mk}}}\sqrt{{{p}_{mk}}}{{{\bar{v}}}_{mk}} \right|}^{2}}}{\sigma _{k}^{2}+Z_{k}^{\left( \text{t,r} \right)}} \right)+ \\ & \sum\limits_{m=1}^{{{K}_{\text{t}}}}{\frac{{{\tau }_{m}}\left| A \right|}{{{P}_{\text{tot}}}}}\left( \text{tr}(\xi _{m}^{\left( \text{t} \right)})+\sum\limits_{k\in {{D}_{m}}}{\|{{w}_{mk}}{{\|}^{2}}} \right)-1 \\ \end{align}$ | (14) |
其中τm为拉格朗日乘子. 由KKT条件,即对拉格朗日函数求偏导$\frac{\partial L}{\partial {{p}_{mk}}}=0$得
| $\begin{align} & {{p}_{mk}}=\frac{\sigma _{k}^{2}+Q}{{{\left| h_{k}^{\text{H}}{{C}_{k}}{{D}_{k}}{{{\bar{v}}}_{k}} \right|}^{2}}}g_{k}^{'-1}\left( \frac{\sigma _{k}^{2}+Q}{{{\alpha }_{k}}{{\left| h_{k}^{\text{H}}{{C}_{k}}{{D}_{k}}{{v}_{k}} \right|}^{2}}}\left( \frac{{{\tau }_{m}}\left| A \right|}{{{P}_{\text{tot}}}} \right.\times \right. \\ & \left. \left. {{{\bar{v}}}_{mk}}\bar{v}_{mk}^{\text{H}}+\frac{{{\tau }_{m}}\left| A \right|}{{{P}_{\text{tot}}}}\sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{D}_{mk}}{{{\bar{v}}}_{mk}}\bar{v}_{mk}^{\text{H}}D_{mk}^{\text{H}}{{T}_{j}}} \right) \right)/\left| A \right| \\ \end{align}$ | (15) |
其中
| $\begin{align} & Q=\sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{1}{\sigma _{i}^{2}}}b_{k}^{2}h_{mi}^{\text{H}}{{C}_{mi}}{{D}_{mk}}D_{mk}^{\text{H}}C_{mi}^{\text{H}}{{h}_{mi}}+ \\ & \sum\limits_{i=1}^{{{K}_{\text{r}}}}{\frac{1}{\sigma _{i}^{2}}}h_{mi}^{\text{H}}{{C}_{mi}}\left( \sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{D}_{mk}}D_{mk}^{\text{H}}{{T}_{j}}} \right)C_{mi}^{\text{H}}{{h}_{mi}} \\ \end{align}$ |
由上述分析可知,在计算出次优波束形成导向矢量$\bar{v}_{mk}^{\left( L \right)}$和功率分配pmk的基础上可设计SLNR波束形成器为
| $\begin{align} & w_{mk}^{\text{sub}}=\frac{{{{\bar{v}}}_{mk}}}{\|{{{\bar{v}}}_{mk}}{{\|}_{2}}}~\frac{\sigma _{k}^{2}+Q}{{{\left| h_{k}^{\text{H}}{{C}_{k}}{{D}_{k}}{{{\bar{v}}}_{k}} \right|}^{2}}}g_{k}^{'-1}\left( \frac{\sigma _{k}^{2}+Q}{{{\alpha }_{k}}|h_{k}^{\text{H}}{{C}_{k}}{{D}_{k}}{{{\bar{v}}}_{k}}{{|}^{2}}}\times \right. \\ & \frac{\left( \frac{{{\tau }_{m}}\left| A \right|}{{{P}_{\text{tot}}}}{{{\bar{v}}}_{mk}}\bar{v}_{mk}^{\text{H}}+\frac{{{\tau }_{m}}\left| A \right|}{{{P}_{\text{tot}}}}\sum\limits_{j=1}^{{{N}_{m}}}{a_{j}^{2}T_{j}^{\text{H}}{{D}_{mk}}{{{\bar{v}}}_{mk}}\bar{v}_{mk}^{\text{H}}D_{mk}^{\text{H}}{{T}_{j}}} \right)}{\left| A \right|} \\ \end{align}$ | (16) |
下面通过仿真来验证提出的计及收发信机射频损伤的UDN协同波束形成器的性能. 仿真参数设定:UDN中用户数Kr=4,基站数Kt=4,每个基站安装天线Nm=4(m=1,2,3,4),每个用户终端为单天线;系统效用函数采用加权最大/最小公平性函数$f\left( g \right)=\min ~\frac{{{g}_{k}}}{{{\beta }_{k}}},\forall k,k\in {{K}_{\text{r}}}$;用户性能函数gk(Ik)=lb(1+Ik);信道服从瑞利衰落,噪声方差σ2=1. 收发信机的射频损伤为${{\eta }_{j}}\left( x \right)=E_{j}^{\left( \text{t} \right)}x={{a}_{j}}x{{\nu }_{k}}\left( x \right)=E_{k}^{\left( \text{r} \right)}x={{b}_{k}}x$,假设$E_{j}^{\left( \text{t} \right)}=E_{k}^{\left( \text{r} \right)}=0.15$.
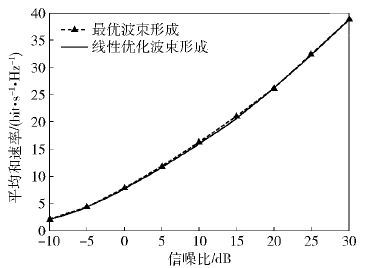
图 1比较了最优波束形成和次优波束形成方法的系统和速率. 可以看出,所提出的线性次优波束形成器所获得的和容量逼近最优容量.
|
图 1 最优和次优波束形成的和速率 |
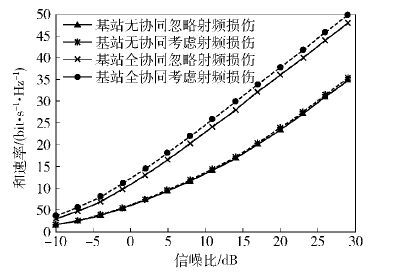
图 2给出了考虑和忽略收发信机射频损伤时,不同数量基站协同波束形成的和速率. 可以看到,基站间全部参与协同波束形成可消除小区间干扰而提高UDN和容量;且考虑收发信机射频损伤时,由于采用了更准确的协同波束形成模型,进一步减小射频损伤对信号的畸变,从而提高UDN容量.
|
图 2 基站间协同波束形成的和速率 |
图 3分别给出了忽略收发信机射频损伤、仅知接收端射频损伤、仅知发送端射频损伤以及已知收发信机射频损伤情况下,4基站协同波束形成的UDN和速率. 可以看到,若已知接收端/发送端射频损伤,UDN协同波束形成的和速率更高,特别地,当发送、接收端射频损伤均知的情况下,协同波束形成的UDN和速率最大.

|
图 3 不同射频损伤的系统和速率 |
研究了同时考虑收发信机射频损伤的UDN协同波束形成问题. 首先,建立了考虑射频损伤的UDN协同波束形成系统模型,并采用凸优化方法求解得到最优波束形成器;然后,基于最优波束形成器的结构特征,设计由SLNR波束形成导向矢量和功率分配构成的线性次优波束形成器. 仿真结果表明,由于同时考虑到收发信机射频损伤,可更准确地建立UDN协同波束形成模型,补偿射频损伤对收发信号的影响而提高UDN协同波束形成系统容量.
| [1] | 方正, 李艳, 黎海涛, 等. 超密集网络空域协同波束形成研究[J]. 电子科技大学学报 , 2015 . Fang Zheng, Li Yan, Li Haitao, et al. Spatial coordination beamforming for ultra-dense wireless networks[J]. Journal of University of Electronic Science and Technology of China , 2015 . |
| [2] | Jose J, Prasad N, Khojastepour M, et al. On robust weighted-sum rate maximization in MIMO interference networks[C]//International Conference on Communications. Kyoto: IEEE, 2011: 1-6. |
| [3] | Du Bo, Chen Ming, Zhang Wence, et al. Optimal beamforming for single group multicast systems based on weighted sum rate[C]//International Conference on Communications. Budapest: IEEE, 2013: 4921-4925. |
| [4] | Li Weichiang, Chang Tsunghui, Lin Che, et al. A convex approximation approach to weighted sum rate maximization of multiuser MISO interference channel under outage constraints[C]//ICASSP. Prague: IEEE, 2011: 3368-3371. |


