2. 北京邮电大学 信息与通信工程学院, 北京 100876
针对多输入多输出(MIMO)系统,提出了一种基于Tucker-2模型的联合信号检测与信道估计方法.所提方法在信源端对每个发送信息符号进行三维编码,该编码方式不仅能获得空间和时间分集,并且使得信源发送信号具备盲检测特性.在信宿端,所提方法通过对接收信号构造Tucker-2模型,并设计2种接收算法拟合该模型,从而实现了信息符号和信道的联合估计.理论分析与仿真结果表明,在未知信道状态信息的条件下,所提方法能有效地检测信号,并同时估计出信道状态信息;与传统的导频辅助信道估计方法相比,所提方法具有更好的信道估计精度.
2. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
A Tucker-2 model based scheme for joint signal detection and channel estimation in multiple-input multiple-output (MIMO) systems was presented. At the source node, the proposed scheme uses three-way coding for each information symbol. This coding approach can achieve space and time diversity, and it makes the transmitted signal built-in blind detection property. The received signal at the destination node is formulated as a Tucker-2 model, and then two receiver algorithms are proposed for joint signal detection and channel estimation. The theory analysis and computer simulation shows that the proposed scheme can jointly estimate the signal and the instantaneous channel state information. Compared with existing approach of pilot symbol-assisted channel estimation, the proposed scheme has higher estimation accuracy.
与单天线系统相比,多输入多输出(MIMO,multiple-input multiple-output)系统[1]在不增加传输带宽和功率的情况下,能大幅度提高传输速率和可靠性,已经得到了广泛的研究和应用. 多维信号处理技术[2-3]利用信号的空域、时域、频域和码域等维度间的特定结构,在分解唯一性的基础上,通过拟合所构造的多维矩阵模型,无需或仅需少量的信道状态信息(CSI,channel state information)和编码矩阵等信息,就能实现信号检测和信道估计. 已有研究表明,多维信号处理技术应用于MIMO系统能进一步提高通信系统的频谱效率和可靠性[4-8].
Sidiropoulos等[4]针对MIMO系统,利用所设计的Khatri-Rao空-时编码方案,提出了一种基于平行因子(PARAFAC)模型的联合接收机,该接收机能实现信号与信道的联合估计. De[5]通过利用时变Khatri-Rao空-频编码方案,提出了一种半盲接收机. De等[6]在文献[4-5]的基础上,提出了一种基于空-时-频编码的半盲接收机设计方案. Du等[7]针对MIMO中继系统,利用所设计的多组Khatri-Rao空-时编码方案,提出了一种半盲接收机,该半盲接收机能联合估计信息符号、信源-中继信道和中继-信宿信道的CSI. 在文献[7]的基础上,Ximenes等[8]考虑了中继编码方式,提出了一种基于内嵌式PARAFAC模型的联合接收机. 虽然上述多维信号处理方法都能有效地实现信号与信道的联合估计,但由于它们都基于PARAFAC模型,因此需要固定信息矩阵的某一列或某一行来消除尺度模糊[2]. 而且,上述文献中的方法要求发送数据流的数目必须等于信源端天线的数目.
在MIMO系统中,为了更好地实现信号与信道的联合估计,笔者提出了一种基于Tucker-2模型[9-10]的联合信号检测与信道估计方法. 所提方法在信源端对每一个信息符号进行编码,在信宿端对接收信号构造Tucker-2模型,并设计了迭代的Tucker-2交替最小二乘(T-ALS,Tucker-2 alternating least squares)算法与闭合的Tucker-2奇异值分解(T-SVD,Tucker-2 singular value decomposition)算法对该模型进行拟合,从而实现信号和信道的联合估计.
1 系统模型考虑如图 1所示的MIMO系统,发射端和接收端分别配置MS和MD根天线. 发射端传输的信息符号为sn,r,其中n=1,2,…,N,r=1,2,…,R. sn,r表示第r个数据流中的第n个信息符号,每一个数据流由N个信息符号构成.

|
图 1 系统模型框图 |
在发射端采用三维扩展码cms,r,p对每一个信息符号sn,r进行编码,其中ms=1,2,…,Ms,p=1,2,…,P. 对于第p个码片,第n个时隙中第ms根天线上的发射信号可表示为
| ${{x}_{{{m}_{s}},n,p}}=\sum\limits_{r=1}^{R}{{{c}_{{{m}_{s}},r,p}}{{s}_{n,r}}}$ | (1) |
其中:xms,n,p和cms,r,p分别为三维矩阵$X\in {{\mathbb{C}}^{{{M}_{S}}\times N\times P}}$和$C\in {{\mathbb{C}}^{{{M}_{S}}\times R\times P}}$中的典型元素[3],sn,r为矩阵$S\in {{\mathbb{C}}^{N\times P}}$中的对应元素.
对于第p个码片,第n个时隙中第mD根天线上的接收信号可表示为
| $\begin{align} & {{y}_{{{m}_{D}},n,p}}=\sum\limits_{{{m}_{S}}=1}^{{{M}_{S}}}{{{h}_{{{m}_{D}},{{m}_{S}}}}}{{x}_{{{m}_{S}},n,p}}+{{v}_{{{m}_{D}},n,p}}= \\ & \sum\limits_{{{m}_{S}}=1}^{{{M}_{S}}}{\sum\limits_{r=1}^{R}{{{h}_{{{m}_{D}},{{m}_{S}}}}}}{{c}_{{{m}_{S}},r,p}}{{s}_{n,r}}+{{v}_{{{m}_{D}},n,p}} \\ \end{align}$ | (2) |
其中:ymD,n,p和vmD,n,p分别为三维接收信号矩阵$Y\in {{\mathbb{C}}^{{{M}_{D}}\times N\times P}}$和三维噪声信号矩阵$V\in {{\mathbb{C}}^{{{M}_{D}}\times N\times P}}$中的典型元素,hmD,mS为信道矩阵$H\in {{\mathbb{C}}^{{{M}_{D}}\times {{M}_{S}}}}$中的对应元素.
2 Tucker-2模型式(2)构成了一个含有噪声vmD,n,p的Tucker-2模型[9]. 为了实现信号检测和信道估计,下面首先对所构造的Tucker-2模型进行剖面分析.
三维矩阵模型式(1)和式(2)可分别由2个等价二维矩阵表示. 定义${{C}_{\cdot \cdot p}}\in {{\mathbb{C}}^{{{M}_{S}}\times R}}$为三维扩展码矩阵C中的第p个切片,三维矩阵模型式(1)可表示为
| ${{X}_{\cdot \cdot p}}={{C}_{\cdot \cdot p}}{{S}^{\text{T}}}$ | (3) |
其中${{X}_{\cdot \cdot p}}\in {{\mathbb{C}}^{{{M}_{S}}\times N}}$为三维发射信号矩阵X中的第p个切片. 同理,三维矩阵模型式(2)可表示为
| ${{Y}_{\cdot \cdot p}}=H{{X}_{\cdot \cdot p}}+{{V}_{\cdot \cdot p}}$ | (4) |
其中:${{Y}_{\cdot \cdot p}}\in {{\mathbb{C}}^{{{M}_{D}}\times N}}$和${{V}_{\cdot \cdot p}}\in {{\mathbb{C}}^{{{M}_{D}}\times N}}$分别为三维接收信号矩阵Y和噪声矩阵V的第p个切片. 按列方向分别对矩阵切片集$\{{{Y}_{\cdot \cdot 1}},{{Y}_{\cdot \cdot 2}},\ldots ,{{Y}_{\cdot \cdot P}}\}$和$\{{{Y}^{\text{T}}}_{\cdot \cdot 1},{{Y}^{\text{T}}}_{\cdot \cdot 2},\ldots ,{{Y}^{\text{T}}}_{\cdot \cdot P}\}$进行堆叠,令${{Y}_{1}}={{[{{Y}^{\text{T}}}_{\cdot \cdot 1},{{Y}^{\text{T}}}_{\cdot \cdot 2},\ldots ,{{Y}^{\text{T}}}_{\cdot \cdot P}]}^{\text{T}}}$和${{Y}_{2}}={{[{{Y}_{\cdot \cdot 1}},{{Y}_{\cdot \cdot 2}},\ldots ,{{Y}_{\cdot \cdot P}}]}^{\text{T}}}$,即有
| ${{Y}_{1}}=({{I}_{P}}\otimes H)\left[ \begin{matrix} {{C}_{\cdot \cdot 1}} \\ \vdots \\ {{C}_{\cdot \cdot P}} \\ \end{matrix} \right]{{S}^{\text{T}}}+\left[ \begin{matrix} {{V}_{\cdot \cdot 1}} \\ \vdots \\ {{V}_{\cdot \cdot P}} \\ \end{matrix} \right]~$ | (5) |
| ${{Y}_{2}}=({{I}_{P}}\otimes S)\left[ \begin{matrix} C_{\cdot \cdot 1}^{\text{T}} \\ \vdots \\ C_{\cdot \cdot P}^{\text{T}} \\ \end{matrix} \right]{{H}^{\text{T}}}+\left[ \begin{matrix} V_{\cdot \cdot 1}^{\text{T}} \\ \vdots \\ V_{\cdot \cdot P}^{\text{T}} \\ \end{matrix} \right]$ | (6) |
其中⊗表示Kronecker乘积. 令${{F}_{1}}={{[C_{\cdot \cdot 1}^{\text{T}},C_{\cdot \cdot 2}^{\text{T}},\ldots ,\text{ }C_{\cdot \cdot P}^{\text{T}}]}^{\text{T}}}{{V}_{1}}={{[V_{\cdot \cdot 1}^{\text{T}},V_{\cdot \cdot 2}^{\text{T}},\ldots ,V_{\cdot \cdot P}^{\text{T}}]}^{\text{T}}}{{F}_{2}}={{[{{C}_{\cdot \cdot 1}},{{C}_{\cdot \cdot 2}},\ldots ,\text{ }{{C}_{\cdot \cdot P}}]}^{\text{T}}}$和${{V}_{2}}={{[{{V}_{\cdot \cdot 1}},{{V}_{\cdot \cdot 2}},\ldots ,{{V}_{\cdot \cdot P}}]}^{\text{T}}}$,则式(5)和式(6)可分别表示为
| ${{Y}_{1}}=({{I}_{P}}\otimes H){{F}_{1}}{{S}^{\text{T}}}+{{V}_{1}}~$ | (7) |
| ${{Y}_{2}}=({{I}_{P}}\otimes S){{F}_{2}}{{H}^{\text{T}}}+{{V}_{2}}~$ | (8) |
按行方向对切片向量集$\{\text{vec}({{Y}_{\cdot \cdot 1}}),\text{vec}({{Y}_{\cdot \cdot 2}}),\ldots ,~\text{vec}({{Y}_{\cdot \cdot P}})\}$进行堆叠,令${{Y}_{3}}=[\text{vec}({{Y}_{\cdot \cdot 1}}),\text{vec}({{Y}_{\cdot \cdot 2}}),\ldots ,\text{vec}({{Y}_{\cdot \cdot P}})]$,并利用Kronecker积特性$\text{vec}(AD{{B}^{\text{T}}})=\left( B\otimes A \right)\text{vec}\left( D \right)$,可得
| ${{Y}_{3}}=\left( S\otimes H \right){{\left[ \begin{matrix} {{(\text{vec}({{C}_{\cdot \cdot 1}}))}^{\text{T}}} \\ \vdots \\ {{(\text{vec}({{C}_{\cdot \cdot P}}))}^{\text{T}}} \\ \end{matrix} \right]}^{\text{T}}}+{{\left[ \begin{matrix} {{(\text{vec}({{V}_{\cdot \cdot 1}}))}^{\text{T}}} \\ \vdots \\ {{(\text{vec}({{V}_{\cdot \cdot P}}))}^{\text{T}}} \\ \end{matrix} \right]}^{\text{T}}}$ | (9) |
令${{F}_{3}}=[\text{vec}({{C}_{\cdot \cdot 1}}),\text{vec}({{C}_{\cdot \cdot 2}}),\ldots ,\text{vec}({{C}_{\cdot \cdot P}})]$和${{V}_{3}}=[\text{vec}({{V}_{\cdot \cdot 1}}),\text{vec}({{V}_{\cdot \cdot 2}}),\ldots ,\text{vec}({{V}_{\cdot \cdot P}})]$,式(9)可表示为
| ${{Y}_{3}}=\left( S\otimes H \right){{F}_{3}}+{{V}_{3}}$ | (10) |
式(7)、式(8)和式(10)分别为所构造的Tucker-2模型的3个剖面展开形式.
3 接收算法的设计本节设计了2种接收算法对Tucker-2模型进行拟合,这两种算法分别为迭代的T-ALS接收算法和非迭代的T-SVD接收算法.
3.1 T-ALS接收算法交替最小二乘(ALS,alternating least squares)算法[3]简单易行,且具有较高的拟合精度,因此通常用于拟合PARAFAC模型. 在本小节中,根据ALS算法的思想,设计了一种T-ALS算法对所构造的Tucker-2模型进行拟合.
根据式(7)和式(8),利用交替最小化下列条件最小二乘(LS,least squares)准则来联合估计S和H为
| ${{{\hat{S}}}_{(i)}}=\underset{S}{\mathop{\arg \min }}\,\left\| {{Y}_{1}}({{I}_{P}}\otimes {{H}_{(i-1)}}){{F}_{1}}{{S}^{T}} \right\|_{\text{F}}^{2}$ | (11) |
| ${{{\hat{H}}}_{(i)}}=\underset{H}{\mathop{\arg \min }}\,\left\| {{Y}_{2}}({{I}_{P}}\otimes {{S}_{(i)}}){{F}_{2}}{{H}^{T}} \right\|_{\text{F}}^{2}$ | (12) |
其中:‖·‖F表示Frobenius范数,i为迭代次数,${{{\hat{S}}}_{(i)}}$和${{{\hat{H}}}_{(i)}}$分别为S和H第i次迭代的估计值. 第i次迭代的代价函数表示为
| $\phi \left( i \right)=\|{{Y}_{1}}({{I}_{P}}\otimes {{H}_{(i)}}){{F}_{1}}S_{(i)}^{T}{{\|}_{\text{F}}}~$ | (13) |
所提T-ALS算法的步骤总结如下.
步骤1 初始化${{{\hat{H}}}_{(0)}}$,设i=1和Φ(0)=∞.
步骤2 根据Y1值,计算S的LS估计为
| ${{{\hat{S}}}_{(i)}}={{[{{(({{I}_{P}}\otimes {{H}_{(i\text{-}1)}}){{F}_{1}})}^{\dagger }}{{Y}_{1}}]}^{\text{T}}}$ |
步骤3 根据Y2值,计算H的LS估计为
| ${{{\hat{H}}}_{(i)}}={{[{{(({{I}_{P}}\otimes {{S}_{(i\text{-}1)}}){{F}_{2}})}^{\dagger }}{{Y}_{2}}]}^{\text{T}}}$ |
步骤4 若|Φ(i)-Φ(i-1)|/Φ(i)≤ε(ε=10-5),则迭代结束;否则令i=i+1,跳至步骤2.
该T-ALS算法单次迭代的计算复杂度为O(PMDR2+PNMS2). 所提T-ALS算法的可辨识性问题对于实现信号检测和信道矩阵估计非常重要,具体地说,T-ALS算法在LS意义上的可辨识性与从Y1 和Y2中估计出S和H直接相关.
定理1 (可辨识性条件) 假设信号矩阵S和信道矩阵H为列满秩矩阵,若F1和F2也为列满秩矩阵,则S和H在LS意义上是可辨识的.
证明 由式(7)和式(8)可知,若${{Z}_{1}}=({{I}_{P}}\otimes H){{F}_{1}}\in {{\mathbb{C}}^{P{{M}_{D}}\times R}}$和${{Z}_{2}}=({{I}_{P}}\otimes S){{F}_{2}}\in {{\mathbb{C}}^{PN\times {{M}_{S}}}}$为列满秩矩阵,则S和H在LS意义上是可辨识的. 因为S和H为列满秩矩阵,可知(IP⊗H)和(IP⊗S)也为列满秩矩阵. 此时rank(Z1)=rank(F1)和rank(Z2)=rank(F2),所以F1和F2为列满秩矩阵可确保S和H可辨识,证明完毕.
根据定理1,S、H、F1和F2都为列满秩矩阵可确保S和H是可辨识的,这意味着在系统设计中,扩展码片的长度应满足下列条件:
| $P\ge \max \left\lceil \frac{R}{{{M}_{S}}} \right\rceil ,\left\lceil \frac{{{M}_{S}}}{R} \right\rceil $ | (14) |
其中$\left\lceil \cdot \right\rceil $表示向上取整操作.
3.2 非迭代接收算法由于T-ALS算法采用了迭代的思想,当初始值较差或估计矩阵存在线性相关列时,迭代会陷入局部循环,该算法需要较多的迭代次数来达到收敛[7, 10]. 针对上述问题,本节提出了一种非迭代算法来拟合Tucker-2模型,所提算法具有较低的计算复杂度.
根据式(10)可知,若F3为行满秩矩阵,则有$(\hat{S}\otimes \hat{H})={{Y}_{3}}{{({{F}_{3}})}^{\dagger }}$,其中${\hat{S}}$和${\hat{H}}$为S和H的估计值. 设${{Z}_{3}}=(\hat{S}\otimes \hat{H})\in {{\mathbb{C}}^{N{{M}_{D}}\times R{{M}_{S}}}}$,可得如下向量化形式:
| $\begin{align} & \Gamma =\text{vec}(\hat{S})\otimes \text{vec}(\hat{H})= \\ & {{[{{(\text{vec}({{E}_{1,1}}))}^{\text{T}}},\cdots ,{{(\text{vec}({{E}_{N,R}}))}^{\text{T}}}]}^{\text{T}}} \\ \end{align}$ | (15) |
其中:$\Gamma \in {{\mathbb{C}}^{N{{M}_{D}}P{{M}_{S}}\times 1}}$,${{E}_{n,r}}={{{\hat{s}}}_{n,r}}\hat{H}\in {{\mathbb{C}}^{{{M}_{D}}\times {{M}_{S}}}}$. 因为
| $\begin{align} & \left\| {{Z}_{3}}-(\hat{S}\otimes \hat{H}) \right\|_{\text{F}}^{2}=\left\| \Gamma -\text{vec}(\hat{S})\otimes \text{vec}(\hat{H}) \right\|_{2}^{2}= \\ & \left\| \text{unvec}(\Gamma )\text{vec}(\hat{H}){{(\text{vec}(\hat{S}))}^{\text{T}}} \right\|_{\text{F}}^{2} \\ \end{align}$ | (16) |
所以,可根据式(16)的范数等价特性,对Kronecker乘积$(\hat{S}\otimes \hat{H})$进行重新排列,排列成秩1矩阵$\text{unvec}(\Gamma )\in {{\mathbb{C}}^{{{M}_{D}}{{M}_{S}}\times NP}}$. 对unvec(Γ)进行奇异值分解(SVD,singular value decomposition),可得
| $\text{unvec}\left( \Gamma \right)=U\Sigma {{V}^{\text{H}}}$ | (17) |
其中:$U\in {{\mathbb{C}}^{{{M}_{D}}{{M}_{S}}\times {{M}_{D}}{{M}_{S}}}}$和$V\in {{\mathbb{C}}^{NP\times NP}}$为酉矩阵,$\Sigma \in {{\mathbb{C}}^{{{M}_{D}}{{M}_{S}}\times NP}}$为对角矩阵. 由于nvec(Γ)为秩1矩阵,可得
| $\text{unvec}\left( \Gamma \right)\approx {{U}_{_{\cdot }1}}{{\sigma }_{1}}V_{_{\cdot }1}^{\text{H}}$ | (18) |
其中:σ1为最大奇异值,${{U}_{_{\cdot }1}}\in {{\mathbb{C}}^{{{M}_{D}}{{M}_{S}}\times 1}}$和${{V}_{_{\cdot }1}}\in {{\mathbb{C}}^{NP\times 1}}$分别为U和V的第1列. 在存在尺度模糊的情况下,可得$\text{vec}(\hat{S})\approx \alpha V_{.1}^{*}$和$\text{vec}(\hat{S})\approx \alpha V_{.1}^{*}\text{vec}(\hat{H})\approx (1/\alpha ){{\sigma }_{1}}{{U}_{_{\cdot }1}}$,其中α为尺度模糊因子. 在实际通信中,可以通过发射一个已知信息符号s1,1=1来消除这种尺度模糊. 此时α=1/v1,1* 即有
| $\left. \begin{align} & \text{vec}(\hat{S})\approx V_{.1}^{*}/v_{1.1}^{*} \\ & \text{vec}(\hat{H})\approx {{\sigma }_{1}}{{U}_{_{\cdot }1}}v_{1.1}^{*} \\ \end{align} \right\}$ | (19) |
由上述分析可知,所提T-SVD算法的总计算复杂度为O(MSRP2+MDMSNP),其中前一项为求取F3伪逆的计算复杂度,后一项为秩-1矩阵unvec(Γ)SVD的计算复杂度.
4 仿真分析为了验证所提算法的性能,通过Matlab对所提算法进行了蒙特卡罗仿真,并与传统的基于导频训练算法和非盲检测算法进行了比较. 所提算法的性能由信号检测的误比特率(BER,bit error rate)和信道估计的精度进行衡量. 假设信道H中的元素都是均值为0,方差为1的独立同分布的随机变量. 信道H的估计精度由归一化均方误差(NMSE,normalized mean square error)进行表征,发送符号采用正交相移键控调制方式.
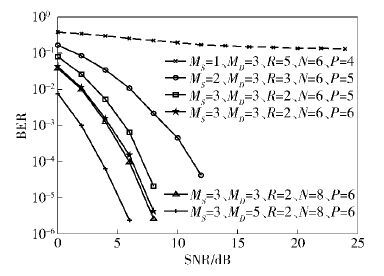
图 2给出了不同系统参数下,所提T-ALS算法的BER性能. 图 2显示,当MS=1,MD=3,R=3,N=6,P=5时,所提算法在不同信噪比(SNR,signal to noise ratio)下都具有较高的BER,这是因为该系统参数不满足T-ALS算法的可辨识条件,所以所提算法不能有效地进行信号检测. 图 2表明,对于满足T-ALS算法可辨识条件的其他系统参数,随着SNR的增加,所提算法的BER逐渐减小,其能有效地进行信号检测. 图 2还表明,当接收天线数目MD、信号长度N 或码片数目P增加时,所提算法的BER相应减小,其信号检测能力增强. 图 3给出了不同系统参数下,所提T-ALS算法的信道估计性能. 与图 2一致,图 3表明,对于满足可辨识条件的其他系统参数,所提T-ALS算法具有较好的信道估计性能. 此外,当M
|
图 2 不同系统参数下,所提T-ALS算法的BER性能 |

|
图 3 不同系统参数下,所提T-ALS算法的NMSE性能 |
图 4给出了所提T-SVD算法、所提T-ALS算法、传统的导频辅助算法和非盲检测算法的BER曲线,其中给定系统参数MS=MD=R=2,N=6. 图 4表明,当P=6时,上述4种算法都能有效地检测信号,其中非盲检测算法性能最好,所提T-ALS算法次之,导频辅助算法优于所提T-SVD算法. 然而值得注意的是,与导频辅助算法相比,所提T-SVD算法无须发送导频信号,因此具有更高的频谱效率;与所提T-ALS算法相比,由于T-SVD算法是一种非迭代算法,因此具有较低的复杂度. 图 4还表明,随着P值的增加,所提T-ALS算法的BER相应降低,具有更好的信号检测性能.

|
图 4 不同算法的BER性能比较 |
图 5给出了与图 4对应的NMSE性能曲线. 由于非盲检测算法信道的NMSE恒为0,因此没有出现于图 5中. 图 5表明,所提T-SVD算法、所提T-ALS算法、传统的导频辅助算法都能有效地估计信道. 当P=6时,所提T-ALS算法和所提T-SVD算法的信道估计性能都优于导频辅助算法. 图 5还表明,增加P值能有效地提高所提T-SVD算法的信道估计性能.

|
图 5 不同算法的NMSE性能比较 |
针对MIMO系统,提出了一种基于Tucker-2模型的联合信号检测与信道估计方法. 在未知CSI的条件下,所提方法能有效地检测信号,并同时估计出CSI;与已有方法相比,所提方法具有更好的信号检测性能和信道估计精度;所提方法设计灵活,可根据实际情况选择合适的算法. 仿真结果验证了所提方法的有效性.
| [1] | Zheng Lizhong, Tse D N C. Diversity and multiplexing: a fundamental tradeoff in multiple-antenna channels[J]. IEEE Transactions on Information Theory , 2003, 49 (5) :1073–1096. doi:10.1109/TIT.2003.810646 |
| [2] | Sidiropoulos N D, Giannakis G B, Bro R. Blind PARAFAC receivers for DS-CDMA systems[J]. IEEE Transactions on Signal Processing , 2000, 48 (3) :810–823. doi:10.1109/78.824675 |
| [3] | Lahat D, Adali T, Jutten C. Multimodal data fusion: an overview of methods, challenges, and prospects[J]. Proceedings of the IEEE , 2015, 103 (9) :1449–1477. doi:10.1109/JPROC.2015.2460697 |
| [4] | Sidiropoulos N D, Budampati R S. Khatri-Rao space-time codes[J]. IEEE Transactions on Signal Processing , 2002, 50 (10) :2396–2407. doi:10.1109/TSP.2002.803341 |
| [5] | De Almeida A L F. Blind joint detection and channel estimationin space-frequency diversity systems using time-varying linear constellation precoding[C]//Proc Brazilian Telecommun. Symp (SBrT'11). Brazil:[s. n. ], 2011: 1-5. |
| [6] | De Almeida A L F, Favier G. Double Khatri-Rao space-time-frequency coding using semi-blind PARAFAC based receiver[J]. IEEE Signal Processing Letters , 2013, 20 (5) :471–474. doi:10.1109/LSP.2013.2248149 |
| [7] | Du Jianhe, Yuan Chaowei, Zhang Jinbo. Semi-blind parallel factor based receiver for joint symbol and channel estimation in amplify-and-forward multiple-input multiple-output relay systems[J]. IET Communications , 2015, 9 (6) :737–744. doi:10.1049/iet-com.2014.0553 |
| [8] | Ximenes L R, Favier G, De Almeida A L F. Semi-blind receivers for non-regenerative cooperative MIMO communications based on nested PARAFAC modeling[J]. IEEE Transactions on Signal Processing , 2015, 63 (18) :4985–4998. doi:10.1109/TSP.2015.2454473 |
| [9] | Favier G, De Almeida A L F. Overview of constrained PARAFAC models[J]. EURASIP Journal on Advances in Signal Processing , 2014, 2014 (1) :1–25. doi:10.1186/1687-6180-2014-1 |
| [10] | Phan A H, Tichavsky P, Cichocki A. Tensor deflation for CANDECOMP/PARAFAC-part I: alternating subspace update algorithm[J]. IEEE Transactions on Signal Processing , 2015, 63 (22) :5924–5938. doi:10.1109/TSP.2015.2458785 |


