2. 南京师范大学 地理科学学院, 南京 210046
凸组合最小均方(CLMS)算法能够克服传统最小均方算法收敛速率、跟踪性能和稳态误差之间的矛盾.但传统CLMS算法使用最速下降法推导参数导致其搜索路径呈“之”字形而使收敛速率变慢,为了解决这个问题,采用共轭梯度法实现参数的更新,同时使用双曲正切函数拟合Sigmoid函数来降低算法的运算复杂度.为进一步提高算法性能,在所设计的基础上附加瞬时转移结构实现优化.仿真结果证明,改进算法与传统CLMS、变步长CLMS相比,在噪声、相关信号输入以及非平稳环境下能够保持较好的均方性能和跟踪性能.
2. School of Geography Science, Nanjing Normal University, Nanjing 210046, China
The convex combination of least mean square(CLMS) algorithm can overcome the contradiction between convergence rate, tracking performance and steady state error of traditional least mean square algorithm. However, in the normal adaptive CLMS algorithm, the rule for modifying mixing parameter is based on the steepest descent method. When the algorithm converges, it will generate zigzag phenomena, which can make the convergence speed become slowly. In order to solve this problem, a new rule based on the conjugate gradient method is proposed in this paper. At the same time, modified hyperbolic tangent function is used to reduce computational complexity. Meanwhile, instantaneous transfer scheme is used to further optimize the performance. Theoretical analysis and simulation results demonstrate that under different simulation environment, the proposed algorithm performs good property of mean square and tracking compared with the traditional CLMS and variable step-size CLMS algorithms.
自适应滤波[1-2]是信号处理的关键技术,能够自适应地调整滤波器的结构和参数,使得滤波器在未知环境中有效稳定的工作.
为了更好地解决滤波器收敛速率、跟踪性能和稳态误差之间的矛盾,GarCía提出了一种凸组合最小均方(CLMS,convex combination of least-mean-square)滤波器算法[3-8].在文献[4]中已经证明CLMS算法结构在稳态时至少能与性能较好的滤波器保持一致,在一定条件下要优于独立滤波器.
为了减小运算复杂度,笔者选取S型双曲正切函数,在拟合Sigmoid函数后对该Sigmoid函数进行替换,另外使用共轭梯度法重新设计混合参数的计算.在此基础上,再辅助瞬时转移[6-7]结构可以进一步优化算法性能.
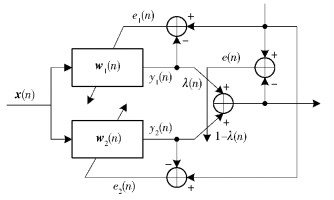
1 CLMS算法CLMS算法原理如图 1所示.其中,d(n)为期望响应,y(n)为滤波器的等效输出信号,e(n)为整个滤波器的等效误差,x(n)为输入信号,w1(n)和w2(n)分别为两个滤波器的权向量,y1(n)和y2(n)分别为两个滤波器的输出,e1(n)和e2(n)分别为两个滤波器产生的误差,λ(n)为CLMS算法的联合参数.为论述方便,假设第1个滤波器为大步长快速收敛的.
|
图 1 CLMS算法原理图 |
由算法图示和原理可以得出,CLMS的工作方式:当自适应刚开始或当系统刚发生时变时,大步长滤波器具备更好的工作特性,算法通过改变λ(n)取值趋近1使组合滤波器呈现更好的收敛速率;当系统处于稳态时,小步长滤波器有着更优的稳态性能,算法使λ(n)接近0来使组合滤波器有更低的稳态误差.通过这种改变联合参数的方式使CLMS的系统性能更好.
2 改进的CLMS算法 2.1 联合参数λ(n)的改进双曲正切函数的表达式为
| $f\left( x \right) = \tanh \left( x \right)$ | (1) |
使用该函数拟合CLMS算法的联合参数表达式,最终得到修正后的双曲正切函数表达式为
| $\lambda \left( n \right) = \frac{1}{2}\left[ {\tanh \left( {Aa\left( h \right)} \right) + 1} \right]$ | (2) |
其中:A为曲线控制参数,a(n)为控制联合参数λ(n)的混合参数.
图 2为当A分别取0.4、0.5、0.6时修正双曲正切函数与Sigmoid函数的对比图.可以看出,修正后的双曲正切函数可以很好地拟合Sigmoid函数,当A=0.5时完全与Sigmoid函数重合.同时,可以通过调整参数A的取值来适应不同的情况,当要求对均方误差有更快的响应速度时可以适当增大A的取值;若外界干扰较为严重,需要系统对外界干扰有更好的稳定性时,取较小的A值可以更好地满足要求.

|
图 2 A不同取值时修正双曲正切函数与Sigmoid函数的对比 |
从图 2的曲线中可以看出,Sigmoid函数在边界处有着更快收敛于边界值的特点,这使得CLMS算法实际效能有较大的损失,因此需要对a(n)进行限制.而修正后的双曲正切函数能够通过改变A的取值得到更加平稳趋于边界值的曲线,可以更好地趋近算法的平稳状态.
2.2 混合参数a(n)的改进依据共轭梯度原理推导参数a(n)的更新公式过程如下.
对a(n)取初始点e2(0),初始方向p(0)=-∇f(e2(0)),n=0;然后沿着已有的共轭方向p(n)进行一维搜索:
| $a\left( {n + 1} \right) = a\left( n \right) + p\left( n \right)$ | (3) |
得到下一个迭代点,并构造新的方向:
| $p\left( {n + 1} \right) = - \nabla f\left( {{e^2}\left( {n + 1} \right)} \right) + {\alpha _n}p\left( n \right),n = n + 1$ | (4) |
其中:
| $\begin{gathered} {\alpha _n} = \frac{{\nabla f\left( {{e^2}{{\left( {n + 1} \right)}^{\text{T}}}} \right)\nabla f\left( {{e^2}\left( {n + 1} \right)} \right)}}{{\nabla f{{\left( {{e^2}\left( n \right)} \right)}^{\text{T}}}\nabla f\left( {{e^2}\left( n \right)} \right)}} = \hfill \\ \frac{{{{\left\| {\nabla f\left( {{e^2}\left( {n + 1} \right)} \right)} \right\|}^2}}}{{{{\left\| {\nabla f\left( {{e^2}\left( n \right)} \right)} \right\|}^2}}} \hfill \\ \end{gathered} $ | (5) |
| $\begin{gathered} \nabla f\left( {{e^2}\left( n \right)} \right) = \hfill \\ - 2e\left( n \right)\left[ {{y_1}\left( n \right) - {y_2}\left( n \right)} \right]\lambda \left( n \right)\left[ {1 - \lambda \left( n \right)} \right] \hfill \\ \end{gathered} $ | (6) |
当初始点远离最优点时传统的共轭梯度法收敛效果可能会不理想.为了解决这个问题,对其改进后得到更新公式为
| $a\left( {n + 1} \right) = a\left( n \right) + {\mu _b}p\left( n \right)$ | (7) |
其中μb为一维搜索步长.
2.3 利用瞬时转移结构优化算法性能在传统CLMS算法的收敛过程中,当快速滤波器达到稳态时组合输出会停滞在此处直到慢速滤波器达到相同的稳态时才继续收敛.为了解决这个问题且使所提算法性能提升更为明显,附加以瞬时转移结构[6-7]优化算法性能.该结构的具体实现:当λ(n)的取值大于λ+,即组合滤波器的性能依赖于大步长快速滤波器的收敛性能时,定义一个N0的取值,使得在该阶段中系统每隔N0次迭代就令慢速滤波器的权值等于快速滤波器的权值,即w2(n+1)=w1(n+1).
瞬时转移结构的使用可以让慢速滤波器的均方误差性能紧跟快速滤波器,当系统在达到快速滤波器稳态后及时进入慢速滤波器的收敛阶段,克服等待的问题从而加快收敛提前进入平稳状态.对于N0的取值,为了使慢速滤波器能够实时地进行权值同步,N0的值越小越好,因此,为了达到良好效果通常取N0=2.
3 仿真实验为了验证算法的性能,现将传统CLMS算法、所提改进算法、文献[3]变步长算法、附加瞬时转移结构优化的改进算法进行比较.所有算法均同时作用于系统辨识过程中,使用的仿真环境参考文献[5].所有稳态超量均方误差(EMSE,the excess mean squared Error)学习曲线均是200次Monte-Carlo实验得到的平均结果.参数取值:μ1=0.025,μ2=0.0025,A=0.5,μa=80,μb=200.为方便标识及描述,各算法名代表如下.
算法1 传统CLMS算法;
算法2 所提改进的CLMS算法;
算法3 文献[3]采用瞬时转移结构后的算法;
算法4 辅助于瞬时转移结构的算法2.
3.1 高斯白噪声为输入的仿真某待测系统为10阶非递归型滤波器模型,设滤波器长度取模型阶次值.输入服从标准正态分布的高斯白噪声x(n),同时干扰信号与输入信号x(n)不相关,且信噪比为20 dB.
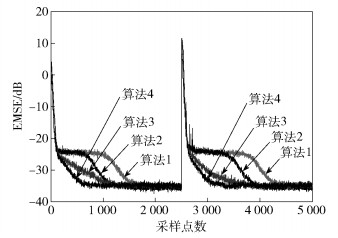
采样点数为5 000,令仿真在迭代至2 500点时权值发生突变以比较算法的跟踪性能.在上述条件下,比较4种算法的EMSE学习曲线如图 3所示.
|
图 3 4种算法在高斯白噪声输入时EMSE(dB)学习曲线 |
由图 3观察得出,通过算法1与算法2的比较表明传统CLMS算法由于最速下降法收敛成“之”字形的原因导致系统的收敛变慢,而由共轭梯度法推导出的参数更新公式使得系统拥有较快的收敛速率;算法3与算法4的比较表明所提进一步优化的CLMS算法继承了改进算法收敛快的特性,使得其固定步长CLMS算法的收敛速率优于文献[3]中变步长CLMS.
3.2 相关信号为输入的仿真设输入信号产生方程式为
| $\mathit{\boldsymbol{x}}\left( n \right) = 0.8\mathit{\boldsymbol{x}}\left( {n - 1} \right) + \mathit{\boldsymbol{r}}\left( n \right)$ | (8) |
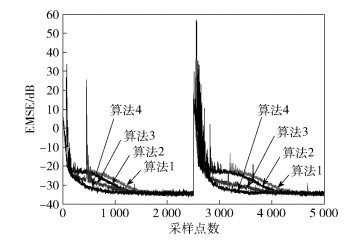
其中r(n)是方差为1的高斯白噪声且与系统的干扰信号独立.其他条件与3.1节中相同.比较4种算法的EMSE学习曲线如图 4所示.
|
图 4 4种算法在相关信号输入时EMSE(dB)的学习曲线 |
由图 4观察得出,当输入相关信号时,4种算法的输出均有相对明显的振荡现象;在收敛方面,各算法收敛速率均慢于3.1节中所述情况,但是算法的整体性能仍容易观测.算法2和算法4均表现出较快的收敛速率和跟踪性能,可以证明所提算法适用于非独立信号环境.
3.3 非平稳环境下的仿真让4种算法分别在非平稳时变系统中进行实验:
| $\mathit{\boldsymbol{w}}\left( {n + 1} \right) = \mathit{\boldsymbol{w}}\left( n \right) + \mathit{\boldsymbol{c}}\left( n \right)$ | (9) |
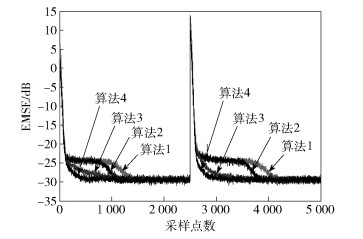
其中:c(n)为高斯白噪声,均值为0,方差为0.01.其他条件与3.1节中相同.比较4种算法的EMSE学习曲线如图 5所示.
|
图 5 4种算法在非平稳环境下时EMSE(dB)的学习曲线 |
由图 5观察得出,在非平稳系统下仿真时,稳态性能劣于3.1节和3.2节中所述的情况.但仍可以发现,所提算法要分别优于传统CLMS算法和文献[3]算法,说明所提算法也能很好地适用于非平稳系统下.
4 结束语采用共轭梯度法重构CLMS算法中混合参数的更新公式,同时利用双曲正切函数拟合Sigmoid函数对联合参数复杂的运算公式进行替换,有效克服了传统算法的缺陷.本算法还可以辅助于瞬时转移结构进一步提升算法的性能.理论分析和仿真结果表明,新算法很好地满足了不同条件下的性能要求,协调了收敛速率与稳态误差以及算法性能与运算复杂度间的矛盾,具有较高的实际应用价值.
| [1] | Huang Boyan, Xiao Yegui, Ma Yaping, et al. A simplified variable step-size LMS algorithm for Fourier analysis and its statistical properties[J]. Signal Processing , 2015, 117 (12) :69–81. |
| [2] | Lu Jing, Qiu Xiaojun, Zou Haishan. A modified frequency-domain block LMS algorithm with guaranteed optimal steady-state performance[J]. Signal Processing , 2014, 104 (6) :27–32. |
| [3] | 洪丹枫, 苗俊, 苏健, 等. 一种变步长凸组合LMS自适应滤波算法改进及分析[J]. 电子学报 , 2014, 42 (11) :2225–2230. Hong Danfeng, Miao Jun, Su Jian, et al. An improved variable step-size convex combination of LMS adaptive algorithm and its analysis[J]. Acta Electronica Sinica , 2014, 42 (11) :2225–2230. |
| [4] | Arenas-Garcia J, Figueiras-Vidal A R, Sayed A H. Mean-square performance of a convex combination of two adaptive filters[J]. IEEE Transactions on Signal Processing , 2006, 54 (3) :1078–1090. doi:10.1109/TSP.2005.863126 |
| [5] | 于霞, 刘建昌, 李鸿儒. 基于箕舌线函数的快速凸组合最小均方算法[J]. 系统仿真学报 , 2010, 22 :1097–1100. Yu Xia, Liu Jianchang, Li Hongru. Fast convex combination of least-mean-square algorithm based on versoria function[J]. Journal of System Simulation , 2010, 22 :1097–1100. |
| [6] | Nascimento V H, De Lamare R C. A low-complexity strategy for speeding up the convergence of convex combinations of adaptive filters[C]//Acoustics, Speech and Signal Processing(ICASSP), 2012 IEEE International Conference on.[S. l.]:IEEE, 2012:3553-3556. |
| [7] | 曾乐雅, 许华, 王天睿. 采用瞬时转移结构的凸组合最小均方算法[J]. 空军工程大学学报(自然科学版) , 2016, 17 (1) :66–71. Zeng Leya, Xu Hua, Wang Tianri. Convex combination of LMS adaptive filtering algorithm using instantaneous transfer scheme[J]. Journal of Air Force Engineering University(Natural Science Edition) , 2016, 17 (1) :66–71. |
| [8] | Sang M J, Seo J H, Park P G. A variable step-size diffusion normalized least-mean-square algorithm with a combination method based on mean-square deviation[J]. Circuits Systems and Signal Processing , 2015, 34 (10) :3291–3304. doi:10.1007/s00034-015-0005-9 |


