为了快速收集传感器节点数据,研究了最短时间聚集汇播的传输调度问题.针对聚集调度中的传输链路选择问题,提出了对数聚集树构造方法,仿照理想情况下的最优聚集树结构对传输链路进行了优化选择;针对聚集调度中的时间片分配问题,提出了基于链路效用的时间片分配方法,以发送节点对其竞争节点的影响作为链路效用,优先为效用值较大的链路分配时间片,增加并行传输.对比实验结果显示,该算法得到的数据收集时延在多数网络部署场景下比现有算法降低10%以上,且在网络密度较大、半径较小的场景中具有更好的相对性能.实验结果表明,新提出的算法是一种有效的快速聚集汇播调度算法.
Aggregation convergecast is an effective data collection pattern of wireless sensor networks. In order to collect sensor data fast, a shortest time aggregation convergecast scheduling problem was investigated. Following the structure of ideal optimal aggregation tree, a logarithmic aggregation tree construction algorithm was proposed for convergecast transmission link selection. For time slot allocation, a link effectiveness based algorithm was presented. In the algorithm, the effectiveness of a link was defined by the influence of the sender to its competitor nodes and time slot was preferentially allocated to those in-tree links with higher value of effectiveness, so as to increase the number of parallel transmission links. Experiments show that the proposed approach can reduce the data collection delay by more than 10% in most scenarios, which verifies the validity of the approach.
无线传感器网络的聚集汇播是指将数据从多个传感器节点向汇聚节点(sink)传输并在传输过程中对数据包进行合并的操作.为了降低聚集汇播的时延,需要对聚集汇播进行调度,从而优化选择数据传输的链路和时间片,使在同一时间片并行传输的链路不产生冲突,且收集网内数据所需的时间最短,该问题即为最短时间聚集汇播调度问题(以下简称聚集调度问题).
现有的聚集调度算法按聚集树的结构主要可分为2类:基于最短路树(SPT,shortest path tree)的算法[1-3]和基于连通支配集(CDS,connected dominating set)的算法[4-7]. 2类算法均存在传输链路向少数节点集中的问题.针对其不足,笔者设计了参照理想最优聚集树结构的聚集树构造方法和基于链路效用的时间片分配方法,避免了传输链路过于集中的问题,增加了并行传输,从而可得更低的数据收集平均时延.
1 网络模型笔者讨论的传感器网络由一个sink和多个传感器节点构成.节点部署在一个2维平面上并形成一个连通网络.每个传感器节点均需要通过多跳无线通信向sink节点传输其检测数据.所有节点均只有一个收发器且只能在单一信道进行半双工通信.
笔者采用协议模型作为节点干扰模型.节点的通信范围和干扰范围均视为以节点为中心的圆形区域.为讨论方便,设每个节点有相同的通信半径(记为R)且干扰半径等于通信半径.当某个接收节点的通信范围之内有超过1个发送节点同时发送数据,则会产生通信碰撞.
用点表示传感器节点,用边表示节点之间的邻接关系,则传感器网络的拓扑结构可用图G=(V, E)描述.其中V为节点集合,E为边集合.在图G中,2个节点之间存在1条边当且仅当它们之间的距离小于等于R.
数据聚集是指多跳传输过程的中间转发节点将其接收到的多条数据与其自身数据进行合并.笔者假设合并后的数据总能封装成一个固定大小的数据包.
由于采用了数据聚集,传感器节点只需要在收到所有需要经过它转发的数据包后进行1次发送即可.最终所有数据均汇集到sink节点.也就是说,每个节点均只通过1条发送链路向其他节点发送数据,而这些链路不应该形成圈(否则数据无法到达sink节点).从图论的角度来看,这些边将形成1棵以sink节点为根的树,笔者称该树为聚集树.
笔者还假设节点之间能通过一定机制实现时间同步,从而可将整个聚集汇播过程的时间线划分为时间片,并为每个节点分配时间片进行分时发送.同时规定,每个时间片的长度相等,且足以完成1个数据包的发送、接收和聚集操作.
2 调度算法聚集调度要解决2个问题,即每个节点应该向哪个节点发送数据,以及在哪个时间片发送数据.它们分别对应着聚集树的构造和时间片的分配.在计算复杂性方面,Chen等[2]已证明聚集调度问题为NP-难,而De等[8]则证明了即使在给定聚集树的基础上进行最优时间片分配仍然是一个NP-完全问题.笔者针对聚集树构造和时间片分配分别设计了启发式算法.
2.1 聚集树构造算法Xu等[6]证明了聚集汇播时延的下限为lbn,其中n为节点数量.如果1棵聚集树能实现在
既然理想最优聚集树能在最短时间内完成聚集汇播,那么可以期待,构造1棵在结构上接近于理想最优树的聚集树将有助于得到较短的汇播时延.在没有给定节点位置和连接关系约束的情况下,1棵包含n个节点的理想最优聚集树可用这样的方式进行构造:从1个节点开始,为每个现有的树中节点添加1个子节点,重复该过程直到节点数达到n.
然而,实际的传感器网络存在给定的网络连接和拓扑结构,聚集树构造算法需要在既有的网络拓扑上进行考虑.仿照上述理想最优聚集树的构造思路,笔者设计了一般网络中的聚集树构造算法,其伪代码如算法1所示.该算法的思路为:从给定的网络中选择链路,逐步生成1棵结构尽可能近似于理想最优聚集树的聚集树.由于这种近似,它将有潜力实现较小的汇播时延.
算法1 对数聚集树构造算法
输入:图G,sink
输出:聚集树T
1. 将sink作为根节点加入T中
2. while节点集合V中仍有节点未加入T
3. for每一个v∈T
4. if {u|u∈N(v), u
5. 从{u|u∈N(v), u
6. 将u作为v的子节点加入T中
7. end-if
8. end-for
9. end-while
10. return T
算法1在每一轮循环中尝试分别为每个树中节点添加1个树外节点作为其子节点.该子节点选为其邻节点中度数最小的点,如此一来,使子节点与父节点之外其他节点之间的链路较少,从而尽可能减少聚集树中链路之间的相互冲突.在理想情况下,该算法的每次循环均可为树中每个节点分别添加1个子节点,如果所有子节点-父节点链路均不相互冲突,则显然该算法构造的聚集树T能在
在介绍链路选择方法之前,首先定义竞争节点集.对于聚集树中的一个发送节点u,定义所有可能与链路(u, F(u))产生冲突的其他树中传输链路的发送节点集为u的竞争节点集,记为CPT(u),并称节点u与CPT(u)中的节点有竞争关系. Yu等[5]给出了节点u的竞争节点集的表达式为
| $ {\rm{CPT}}\left( u \right) = N\left( {F\left( u \right)} \right) \cup \left( {\bigcup\nolimits_{v \in N\left( u \right)\backslash C\left( u \right)} {C\left( v \right)} } \right)\backslash \left\{ {u,F\left( u \right)} \right\} $ | (1) |
其中C(v)为点v的子节点集.
如式(1)所示,1个发送节点的竞争节点集包括其父节点的邻节点和其邻节点的子节点.为了避免链路冲突,具有竞争关系的节点不能在同一个时间片沿着树内链路发送数据.
考虑1条从某个叶节点v到其父节点F(v)的传输链路(v, F(v)),如果将当前时间片分配给该链路,会产生2个方面的影响:一方面是负面影响,即与v有竞争关系的叶节点均无法在当前时间片发送;另一方面是正面影响,即的所有竞争节点均在后续时间片的分配过程中减少1个竞争者.笔者时间片分配算法的思路是,一方面希望当前时间片有更多的并行传输链路;另一方面希望选择这些链路有利于后续时间片的分配.于是,定义链路(v, F(v))的效用Eff为正面影响减去负面影响为
| $ \begin{array}{c} {\rm{Eff}}\left( v \right) = \left| {{\rm{CPT}}\left( u \right)} \right| - \left| {{\rm{CPT}}\left( v \right) \cap {\rm{Lf}}} \right| = \\ \left| {{\rm{CPT}}\left( v \right) \cap \overline {{\rm{Lf}}} } \right| \end{array} $ | (2) |
其中:Lf为叶节点集,链路(v, F(v))的正面影响和负面影响分别用v的竞争节点数量和与v具有竞争关系的叶节点数量表征.而二者相减后得到的效用值即为v的非叶节点竞争节点数量.笔者设计了基于链路效用的时间片分配算法(LEB,link effectiveness based time slot allocation).算法伪代码如算法2所示.LEB算法在每一轮时间片分配过程中优先为效用值较大的发送节点分配时间片,从而增加了并行传输,有利于缩短汇播时延.
算法2 基于链路效用的时间片分配算法
输入:图G,聚集树T
输出:节点的传输目标F,传输时间片S和总体汇播时延Delay
1. t←0
2. while V′中仍存在未调度节点
3. t←t+1
4. Lf←
5. Sender←
6. for每一个节点v∈T
7. if |C(v)|==0
8. Lf←Lf∪{v}
9. end-if
10. end-for
11. for每一个叶节点v∈Lf
12. Eff(v)=|CPT(v)∩Lf|
13. end-for
14. for每一个按Eff值从大到小排列的叶节点v∈Lf
15. if链路(v, F(v))不与时间片t中的已有链路冲突
16. S(v)←t
17. Sender←Sender∪{v}
18. end-if
19. end-for
20. for每一个未调度叶节点u∈Lf∩Sender
21. for u的每一个非叶节点邻居v∈N(u)∩Lf
22. if链路(u, v)不与时间片t中的已有链路冲突
23. S(v)←t
24. F(u)←v
25. Sender←Sender∪{u}
26. break
27. end-if
28. end-for
29. end-for
30. for每一个未调度叶节点u∈Lf∩Sender
31. for u的每一个叶节点邻居v∈N(u)∩Lf
32. if链路(u, v)不与时间片t的已有链路冲突
33. S(v)←t
34. F(u)←v
35. Sender←Sender∪{u}
36. break
37. end-if
38. end-for
39. end-for
40. T←T\Sender
41. end-while
42. Delay←t
43. return F、S和Delay
3 实验分析实验过程中首先生成一个随机部署的传感器网络,然后在该网络上运行聚集调度算法.部署区域取为一个正方形,传感器节点位置坐标在该区域范围内随机生成,sink节点位于正方形区域中央.为便于讨论,所有实验均在连通的网络中进行.
算法性能的讨论需要在不同的实验场景下进行.笔者定义了以下2个参数来描述随机部署的网络场景为
| $ D = n \pi {R^2}/{l^2} $ | (3) |
| $ L = l/R $ | (4) |
其中:n为节点数量,R为节点通信半径,l为正方形区域的边长.记节点密度为D,式(7)将其定义为半径为R的圆形区域中的节点数量,该参数就可用于控制网络中节点的邻居数量. L为部署区域边长与通信半径的比值,该参数可用于控制聚集树的深度.以下实验均以D和L作为实验场景的描述变量.固定r的取值为1,则L=l,于是接下来也直接用L代表区域边长.在以下实验中,对于每一组描述变量均进行20次实验,结果取平均值.
图 5给出了算法总体性能比较.笔者提出的聚集调度算法用LAT-LEB表示.对比算法选为最短路数据聚集算法(SDA,shortest data aggregation)[2]、赋权递增排序聚集调度算法(WIRES,weighted incremental ranking for converge cast with aggregation scheduling)[3]、分布式聚集调度算法(DAS,distributed aggregation scheduling)[5]、基于簇的聚集调度算法(CLU,cluster-based aggregation scheduling)[7],它们有一定的代表性且在现有算法中具有相对较好的性能. 图 5绘制了时延的折线图,并对每个点绘制了95%的置信区间.可以看出,当区域边长L固定时,随着节点密度D的增长,各算法时延基本呈线性增长,笔者算法得到的时延明显低于其他算法(在D>5,L≤4时笔者算法取得的时延比其他算法降低15%以上),且随着D的增加这种优势逐渐扩大.而对比图 5(a)~(c)可以看出,L越小笔者算法的相对优势越明显.尤其当L=2时,如图 5(a)所示,SDA、WIRES、DAS、CLU的时延相差很小,而笔者算法在除D=5以外,与其他算法相比时延降低了26%~54%.
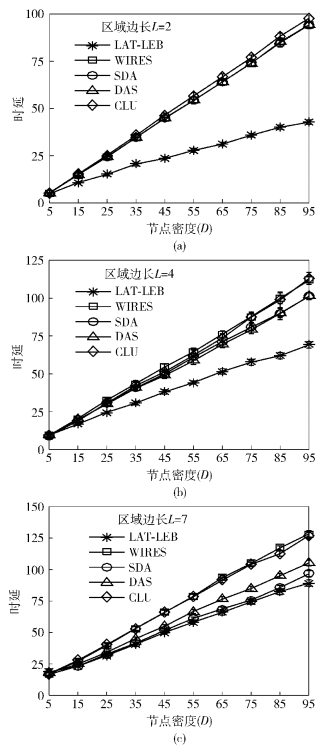
|
图 5 算法总体性能对比 |
总的来说,笔者算法的总体性能优于其他算法,且在节点密度更大、区域边长更小的网络中具有更为明显的优势.
4 结束语研究了无线传感器网络中聚集汇播的传输调度问题,针对传输目标选择和时间片分配2个聚集调度的子问题,分别设计了基于理想最优树结构的对数聚集树构造算法和基于链路效用的时间片分配算法.对比实验显示,聚集调度算法在多数场景下比其他算法缩短了约10%以上.而在节点密度较大、区域边长较长的场景中,新算法具有更大的相对优势,当D=85,L=2时,相对其他算法的性能优势可达50%以上.进一步实验分别评估了聚集调度算法的聚集树构造部分和时间片分配部分,实验结果表明,聚集树构造算法和时间片分配算法能与其他现有算法进行结合并使其性能得到改善.对聚集树拓扑结构的实验讨论显示了新算法构造的聚集树链路比较分散,增加了并行传输从而缩短了时延.综上所述,笔者设计的算法是一种有效的快速聚集汇播调度算法.
| [1] | Incel O D, Ghosh A, Krishnamachari B, et al. Fast data collection in tree-based wireless sensor networks[J]. IEEE Transactions on Mobile Computing , 2012, 11 (1) :86–99. doi:10.1109/TMC.2011.22 |
| [2] | Chen Xujin, Hu Xiaodong, Zhu Jianming. Minimum data aggregation time problem in wireless sensor networks[C]//Proceedings of Mobile Ad Hoc and Sensor Networks. Wuhan:Springer, 2005:133-142. http://link.springer.com/chapter/10.1007/11599463_14 |
| [3] | Malhotra B, Nikolaidis I, Nascimento M A. Aggregation convergecast scheduling in wireless sensor networks[J]. Wireless Networks , 2011, 17 (2) :319–335. doi:10.1007/s11276-010-0282-y |
| [4] | Wan Pengjun, Huang Scottch, Wang Lixin, et al. Minimum-latency aggregation scheduling in multihop wireless networks[C]//Proceedings of the Tenth ACM International Symposium on Mobile Ad Hoc Networking and Computing. New Orleans:ACM, 2009:185-193. http://dl.acm.org/citation.cfm?id=1530773 |
| [5] | Yu Bo, Li Jianzhong, Li Yingshu, et al. Distributed data aggregation scheduling in wireless sensor networks[C]//Proceedings of IEEE Conference on Computer Communications. Rio:IEEE, 2009:2159-2167. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5062140 |
| [6] | Xu Xiaohua, Li Xiangyang, Mao Xufei, et al. A delay-efficient algorithm for data aggregation in multihop wireless sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems , 2011, 22 (1) :163–175. doi:10.1109/TPDS.2010.80 |
| [7] | Guo Longjiang, Li Yingshu, Cai Zhipeng. Minimum-latency aggregation scheduling in wireless sensor network[J]. Journal of Combinatorial Optimization , 2016, 31 (1) :279–310. doi:10.1007/s10878-014-9748-7 |
| [8] | De S E, Nikolaidis I. An exploration of aggregation convergecast scheduling[J]. Ad Hoc Networks , 2013, 11 (8) :2391–2407. doi:10.1016/j.adhoc.2013.06.004 |


