2. 西安邮电大学 通信与信息工程学院, 西安 710061
针对大规模多输入多输出(LS-MIMO)系统最小均方误差(MMSE)检测算法计算复杂度高的问题,提出了基于经典迭代法的低复杂度信号检测算法,包括Jacobi迭代法、高斯-赛德尔迭代法和逐次超松弛迭代法.从精确解的近似值出发,在较少的迭代次数中可获得高效而精确的解,而且计算复杂度相比MMSE检测算法下降一个数量级.仿真结果表明,迭代检测算法经过有限的迭代能够达到近似MMSE检测算法的误码率性能.
2. School of Electronic and Telecommunication Engineering, Xi'an Posts and Telcommunications University, Xi'an 710061, China
For the high computational complexity problem of minimum mean square error(MMSE)detection algorithm on large scale-multiple input multiple output(LS-MIMO)systems, low complexity signal detection algorithm based on the classic iteration method was proposed, including the Jacobi iteration method, Gauss-Seidel iterative method and successive over relaxation iteration method. The proposed algorithm starts from the approximation of an exact solution, obtaining efficient and accurate solution in fewer iterations, and the computational complexity decline an order of magnitudes compared to MMSE detection algorithm. Simulation results show that the iterative detection algorithm can achieve bit error rate performance of approximate MMSE detection algorithm by limit iterations.
大规模多输入多输出(LS-MIMO, large scale-multiple input multiple output)技术已成为下一代移动通信系统的关键技术[1-2],LS-MIMO系统以大规模天线阵列代替现有的多天线,能够同时服务更多的用户[3-4].随着接收端和发射端天线数量成倍增长,传统的检测算法计算复杂度过高,不适合应用在LS-MIMO系统.迭代法具有存储量少、计算量少的优点,研究人员将求解大型线性方程组的共轭梯度(CG,conjugate gradient)迭代算法应用在LS-MIMO系统,经过几次迭代获得近似最小均方误差(MMSE, minimum mean square error)检测算法的误码率(BER,bit error rate)性能[5-6].
笔者提出基于迭代的信号检测算法,将Jacobi迭代法、高斯-赛德尔(GS, Gauss-Seidel)迭代法和逐次超松弛(SOR, successive over relaxation)迭代法应用在信号检测并给出仿真结果和分析.
1 LS-MIMO系统模型假定发送端和接收端天线数量分别为Nt和Nr(Nr>>Nt),接收信号模型为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{n}} $ | (1) |
其中:y、x和n分别为Nr×1维接收信号列向量、Nt×1维发送信号列向量以及Nr×1维独立同分布噪声列向量;H为Nr×Nt平坦瑞利衰落LS-MIMO系统信道矩阵,其中元素hij(i=1, 2, …, Nr,j=1, 2, …, Nt)的均值为0,方差为1,假设获得理想的信道状态信息.
根据文献[5],MMSE算法恢复信号x表示为
| $ \mathit{\boldsymbol{x}} = {\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \sigma _{\rm{n}}^2{\mathit{\boldsymbol{I}}_{{N_{\rm{t}}}}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{W}}^{ - 1}}\mathit{\boldsymbol{\bar y}} $ | (2) |
其中:(·)H和(·)-1分别表示共轭转置和矩阵求逆,y为
| $ \mathit{\boldsymbol{\bar y}} = {\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \sigma _{\rm{n}}^2{\mathit{\boldsymbol{I}}_{{N_{\rm{t}}}}} $ | (3) |
W为
| $ \mathit{\boldsymbol{W}}{\rm{ = }}{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \sigma _{\rm{n}}^2{\mathit{\boldsymbol{I}}_{{N_{\rm{t}}}}} $ | (4) |
σn2为噪声方差,INt为Nt×Nt维单位矩阵.将式(2)稍作变形为
| $ \mathit{\boldsymbol{Wx}} = \mathit{\boldsymbol{\bar y}} $ | (5) |
信号检测算法的实质就是求线性方程组式(5)的解.
2 基于经典迭代法的信号检测算法 2.1 问题描述一般地,考虑如下n元线性方程组:
| $ \mathit{\boldsymbol{AX = b}} $ | (6) |
其中系数矩阵A=(aij)n×n(i=1, 2, …, n,j=1, 2, …, n)非奇异,且A的对角元素aii≠0(i=1, 2, …, n).迭代法的基本思想是根据式(6)设计迭代公式,将任意选择的初始向量X(0)代入,求出X(1),再反复进行迭代得到向量序列.当收敛时,其极限即为原始方程组的解.
对于任意一个Nt×1的非零向量x,式(4)有
| $ {\left( {\mathit{\boldsymbol{Hx}}} \right)^{\rm{H}}}\mathit{\boldsymbol{Hx = }}{\mathit{\boldsymbol{x}}^{\rm{H}}}\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)\mathit{\boldsymbol{x}} > 0 $ | (7) |
说明HHH是正定矩阵,噪声方差σn2是正定的,故W是正定矩阵;又(HHH)T=HHH,说明HHH是对称的,故W也是对称矩阵.因此,可证W对称正定.
根据系数矩阵W对称正定的性质[5],考虑用Jacobi迭代法、GS迭代法和SOR迭代法去求解式(5).
2.2 算法思想Jacobi迭代法将A分裂为A=D+L+U,其中D、L和U分别为A的对角线元素组成的矩阵、A的严格下三角矩阵和A的严格上三角矩阵.由式(6)得到与之等价的方程组,写成矩阵形式为
| $ \mathit{\boldsymbol{X = }} - {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L + U}}} \right)\mathit{\boldsymbol{X + }}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{b}} $ | (8) |
令迭代矩阵记为
| $ \mathit{\boldsymbol{B = }} - {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L + U}}} \right)\mathit{\boldsymbol{,d = }}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{b}} $ | (9) |
取X(0)=(x1(0), x2(0), …, xn(0))T,将其代入式(8)且写成矩阵形式为
| $ {\mathit{\boldsymbol{X}}^{\left( 1 \right)}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}} + \mathit{\boldsymbol{d}} $ | (10) |
再将X(1)代入式(8)中,反复进行迭代运算,得到
| $ {\mathit{\boldsymbol{X}}^{\left( {k + 1} \right)}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{X}}^{\left( k \right)}} + \mathit{\boldsymbol{d,k = }}0,1,2, \cdots $ | (11) |
对式(5)应用Jacobi迭代法,计算过程如表 1所示.
|
|
表 1 Jacobi迭代检测算法计算过程 |
分析Jacobi迭代法发现,每次新计算出来的分量比旧分量更接近方程组的准确解,因此求得新分量后,马上用它来替代旧分量,故GS迭代矩阵为
| $ {\mathit{\boldsymbol{X}}^{\left( {k + 1} \right)}} = - {\left( {\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right)^{ - 1}}\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{X}}^{\left( k \right)}} + {\left( {\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right)^{ - 1}}\mathit{\boldsymbol{b}} $ | (12) |
令迭代阵G=-(D+L)-1U,d1=(D+L)-1b,则
| $ {\mathit{\boldsymbol{X}}^{\left( {k + 1} \right)}} = \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{X}}^{\left( k \right)}} + {\mathit{\boldsymbol{d}}_1},\mathit{\boldsymbol{k = }}0,1,2, \cdots $ | (13) |
GS迭代法的详细计算步骤可参考表 1.
为了加速GS迭代法的收敛,在式(13)修正项前乘以松弛因子w,通过简单计算可得
| $ x_i^{\left( {k + 1} \right)} = x_i^{\left( k \right)} + \frac{{w\left( {{b_i} - \sum\limits_{j = 1}^{i = 1} {{a_{ij}}x_j^{\left( {k + 1} \right)}} - \sum\limits_{j = 1}^n {{a_{ij}}x_j^{\left( k \right)}} } \right)}}{{{a_{ij}}}} $ | (14) |
为保证迭代收敛,取0 < w < 2. SOR迭代矩阵为
| $ \begin{array}{c} {\mathit{\boldsymbol{X}}^{\left( {k + 1} \right)}} = {\left( {\frac{1}{w}\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right)^{ - 1}}\left[ {\left( {\frac{1}{w} - 1} \right)\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{U}}} \right]{\mathit{\boldsymbol{X}}^{\left( k \right)}} + \\ {\left( {\frac{1}{w}\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right)^{ - 1}}\mathit{\boldsymbol{b}} \end{array} $ | (15) |
迭代矩阵记为
| $ {\mathit{\boldsymbol{X}}^{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{L}}_w}{\mathit{\boldsymbol{X}}^{\left( k \right)}} + {\mathit{\boldsymbol{d}}_2},\mathit{\boldsymbol{k = }}0,1,2, \cdots $ | (16) |
SOR迭代法只要选择合适的松弛因子w,收敛速度就会加快,但是最优w的选取比较困难.
3 复杂度分析本节讨论3种迭代算法计算复杂度.发射天线数量Nt=K.
对式(5)应用Jacobi迭代算法,可得迭代方程为
| $ \mathit{\boldsymbol{D}}{{\mathit{\boldsymbol{\hat x}}}^{\left( {k + 1} \right)}} = \mathit{\boldsymbol{\bar y}} - \left( {\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{U}}} \right){{\mathit{\boldsymbol{\hat x}}}^{\left( k \right)}} $ | (17) |
其中
对式(5)应用GS迭代算法,得迭代方程为
| $ \left( {\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right){{\mathit{\boldsymbol{\hat x}}}^{\left( {k + 1} \right)}} = \mathit{\boldsymbol{\bar y}} - \mathit{\boldsymbol{U}}{{\mathit{\boldsymbol{\hat x}}}^{\left( k \right)}} $ | (18) |
同理可得,进行一次GS迭代需要K2次乘法.
对式(5)应用SOR迭代算法,得迭代方程为
| $ \left( {\frac{1}{w}\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}}} \right){{\mathit{\boldsymbol{\hat x}}}^{\left( {k + 1} \right)}} = \left[ {\left( {\frac{1}{w} - 1} \right)\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{U}}} \right]{{\mathit{\boldsymbol{\hat x}}}^{\left( k \right)}} + \mathit{\boldsymbol{\bar y}} $ | (19) |
同理可得,进行一次SOR迭代需要K2+2K次乘法.
计算复杂度如表 2所示,其中i为迭代次数.
|
|
表 2 算法复杂度对比 |
由表 2可以看出,MMSE检测算法涉及矩阵求逆,计算复杂度呈指数增长.相比MMSE检测算法,4种迭代算法复杂度从O(K3)下降到O(K2),约下降了一个数量级.随着迭代次数的增加,迭代算法的计算复杂度成倍增加,但是都保持在O(K2). Jacobi迭代检测算法和GS迭代检测算法复杂度相同,SOR迭代检测算法的复杂度略高于前两种算法,CG迭代检测算法计算复杂度最高.
4 仿真结果天线数量分别取Nr×Nt=64×8和Nr×Nt=128×16,仿真使用瑞利衰落信道,64QAM调制,数据流数量N为38 400.
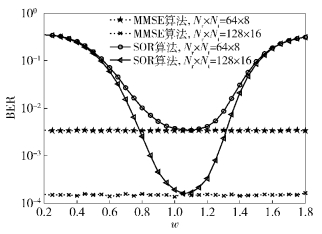
首先分析不同松弛因子w下SOR迭代检测算法和MMSE检测算法的BER性能,信噪比(SNR, signal-to-noise ratio)为4 dB,迭代次数为3,如图 1所示.
|
图 1 不同松弛因子w的BER性能对比 |
由图 1可看出,松弛因子在1.1左右时SOR迭代检测算法最接近MMSE检测算法.当天线数量成倍增加时,SOR迭代检测算法和MMSE检测算法BER性能都相对良好,印证了天线数量增加,虽然计算复杂度成倍增加,却提高了算法的BER性能.因此LS-MIMO系统相同的系统配置,接收天线数量和发射天线数量符合Nr/Nt=8条件,可以选择相同或者相近的松弛因子w.仿真中选w=1.1.
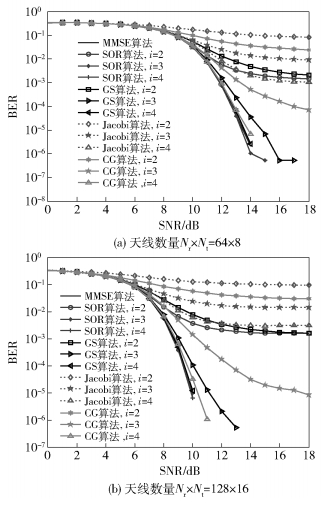
接着给出当天线数量分别为Nr×Nt=64×8和Nr×Nt=128×16时3种迭代检测算法和MMSE检测算法的BER对比,迭代次数为2、3、4.将文献[5]中CG迭代法一同列出,如图 2(a)和图 2(b)所示.
|
图 2 不同天线数量下5种算法的BER对比 |
从图 2(a)中可看出在相同的迭代次数下,SOR迭代检测算法的BER性能最好,收敛速度最快,其次是GS迭代检测算法,接着是CG迭代检测算法,最后是Jacobi迭代检测算法.整体来看,经过4次迭代后,Jacobi迭代检测算法的BER性能和MMSE检测算法相比,BER曲线仍有相当大的差距;CG迭代检测算法经过4次迭代,BER曲线逐渐靠近MMSE检测算法;GS迭代检测算法和SOR迭代检测算法经过4次迭代后最接近MMSE检测算法.当迭代次数为2时,SOR迭代检测算法BER性能比GS迭代检测算法稍好些,但不具有明显优势;当迭代次数为3时,SOR迭代检测算法收敛速度加快,在SNR为14 dB时,SOR迭代检测算法BER比GS迭代检测算法少2.92×10-5,比CG迭代检测算法少4.99×10-5.
对比图 2(b)中的几种算法,可以得到随着天线数量的成倍增加,几种迭代算法的BER性能整体提升,其中CG迭代算法、SOR和GS迭代算法的优势更加明显.
5 结束语以传统MMSE检测算法为基础,将大规模线性方程组的迭代求解算法应用在LS-MIMO系统信号检测,提出了Jacobi迭代检测算法、GS迭代检测算法和SOR迭代检测算法.首先阐述了3种迭代算法的思想;其次分析了3种迭代检测算法的计算复杂度,由分析结果可以看出,Jacobi和GS迭代法有着相同的复杂度,SOR迭代法复杂度比前两种算法稍高,然而相比于MMSE检测算法,3种迭代算法的计算复杂度都下降了一个数量级;最后通过仿真表明经过有限的几次迭代,SOR和GS迭代法能够获得接近MMSE检测算法的BER性能,其中SOR迭代法收敛速度最快.
| [1] | Dai Linglong, Wang Zhaocheng, Yang Zhixing. Next-generation digital television terrestrial broadcasting systems:key technologies and research trends[J]. IEEE Communications Magazine , 2012, 50 (6) :150–158. doi:10.1109/MCOM.2012.6211500 |
| [2] | Ghosh A, Ratasuk R, Mondal B, et al. LTE-advanced:next-generation wireless broadband technology[J]. IEEE Wireless Communications , 2010, 17 (3) :10–22. doi:10.1109/MWC.2010.5490974 |
| [3] | Marzetta T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Transactions on Wireless Communications , 2010, 9 (11) :3590–3600. doi:10.1109/TWC.2010.092810.091092 |
| [4] | Rusek F, Persson D, Lau B K, et al. Scaling up MIMO:opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine , 2013, 30 (1) :40–60. doi:10.1109/MSP.2011.2178495 |
| [5] | Hu Yuting, Wang Zhongxu, Gaol Xinyu, et al. Low-complexity signal detection using CG method for uplink large-scale MIMO systems[C]//Communication Systems(ICCS), 2014 IEEE International Conference on.[S.l.]:IEEE, 2014:477-481. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7024849 |
| [6] | Wu Michael, Yin Bei, Vosoughi Aida, et al. Approximate matrix inversion for high-throughput data detection in the large-scale MIMO uplink[C]//IEEE International Symposium on Circuits & Systems.[S. l.]:IEEE, 2013:2155-2158. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6572301 |


