2. 湖南科技大学 计算机科学与工程学院, 湖南 湘潭 411201 ;
3. 西安通信学院 信息服务系, 西安 710106
为了提高分布式云存储系统的存储可靠性和故障节点修复效率,提出一种基于最小存储再生码的局部性修复编码方案.具体地,构造适用于云存储的系统最小存储再生码,以此码为局部码构造局部性修复编码,确保最大距离可分性质和简单修复特性.性能分析和仿真结果表明,该局部性修复编码方案可实现云存储系统中多个故障节点的快速修复,具有较低的修复局部性,相对于三副本复制方式和简单再生码,该局部性修复编码方案在存储开销和修复带宽开销方面的性能更优.
2. School of Computer Science and Engineering, Hunan University of Science and Technology, Hunan Xiangtan 411201, China ;
3. School of Information Service, Xi'an Communication College, Xi'an 710106, China
In order to improve the reliability of distributed cloud storage system and the efficiency for repairing the failed nodes, a scheme of locally repairable coding based on minimum storage regenerating(MSR) codes was proposed. Specifically, the systematic MSR codes suitable for cloud storage and the locally repairable codes with MSR codes as local codes were constructed respectively to ensure the maximum distance separable(MDS) property and simple repairing characteristics. Performance analysis and simulation show that the locally repairable coding scheme can realize fast repairing of multiple failed nodes in distributed cloud storage system, and has lower repair locality. Compared with three-copy mode and simple regenerating codes, the locally repairable coding scheme has good performances in storage overhead and repair bandwidth overhead.
目前信息技术已经从以计算设备为核心转变为以存储设备为核心,数据海量化成为一种发展趋势,如何快速、高效、可靠地存储这些数据资源成为当下研究的热点和面临的巨大挑战之一.云存储系统可存储海量数据,将成为未来主要的存储方式.如何减少因为数据丢失而产生的修复数据量是云存储系统需要面对的关键问题.
2005年,Acedanski等[1]首次采用网络编码实现数据修复,指出随机线性网络编码不仅能达到与纠删码相同的高可靠性,且存储开销比纠删码更小. 2007年,Dimakis等[2]将分布式存储系统中的节点修复问题抽象成通信网络中的单源多播问题,提出了最小存储再生(MSR, minimum storage regenerating)码和最小带宽再生(MBR, minimum bandwidth regenerating)码.
云存储系统中数据修复的主要性能瓶颈是磁盘I/O开销,该开销与修复过程中连接的节点数目成正比.局部性修复编码(LRC, locally repairable codes)修复节点故障时在确保较低修复带宽的同时,可减少修复过程中连接的节点数,具有较好的修复局部性[3].然而,现有文献讨论的局部性修复编码只能保证对于少数几个故障节点实现快速修复[4-5],还没有给出多个故障节点的快速修复方案,且采用局部性修复编码修复故障节点时没有考虑节点存储开销.
为了实现诸如Hadoop分布式文件系统(HDFS,Hadoop distributed file system)、分布式文件系统(CEPH)、简单存储服务(S3,simple storage service)等云存储系统中故障节点的高效快速修复,显著降低存储节点修复过程中的磁盘I/O开销,达到存储-带宽开销的最佳折中,笔者将再生码和局部性修复编码结合,提出一种适用于分布式云存储系统的基于MSR码的局部性修复编码方案.首先考虑到云存储系统中存储的数据量大,若采用非系统再生码构造局部性修复编码,数据采集节点(DC, data collector)若要获取部分原始数据,需要对整个再生码数据部分进行译码,增加磁盘I/O开销和带宽开销,为此在分布式云存储系统中采用系统MSR码,云存储节点存放原始数据副本.进一步地,将构造的系统MSR码作为局部码,构造局部性修复编码,确保最大距离可分(MDS, maximum distance separable)性质和简单修复特性.性能分析和实验仿真表明,该局部性修复编码方案可实现云存储系统中多个故障节点的快速修复,在存储开销方面的性能优于三副本复制方式和简单再生码,修复局部性接近修复局部性较低的三副本复制方式;相对于里所(RS,reed-solomon)码、三副本复制方式和简单再生码,该局部性修复编码方案在修复带宽开销方面的性能更优.这里需要说明,所谓“快速修复”指的是修复局部性比较小,可通过连接较少的存储节点,实现故障节点数据重构.
1 基于系统MSR码的局部性修复编码 1.1 构造系统MSR码所需的最小有限域为了减少云存储节点的计算和内存开销,降低系统MSR码的编译码复杂度,首先需要确定构造(n, k)系统MSR码所需的最小有限域. Macwilliams[6]已经给出了在k和q给定的情况下,GF(q)上[n, k]MDS码对应矩阵列向量数目n的最大值,如定理1所示.
定理1[6] 给定k和q,对于在GF(q)上的[n, k]MDS码,如果用m(k, q)表示n的最大值,则
当k≥q时,m(k, q)=k+1;当k < q时,有
| $ m(k, q) = \left\{ \begin{array}{l} q + 2, \;\;q为偶数且k=3或k=q-1\\ q + 1, \;\;\;其他 \end{array} \right. $ |
基于此结论,根据定理1,容易得到构造(n, k)系统MSR码所需的最小有限域GF(q),如推论1所示.
推论1 假定分布式云存储系统中存在n个存储节点,大小为B的文件被编码存储在这n个节点中,每个节点存储的数据量为α.为了确保MSR码满足(n, k)MDS特性,确保数据采集者(DC,data collector)从任意k个节点下载数据,能恢复出原始文件,则构造(n, k)系统MSR码所需的最小有限域GF(q)满足:
1)当n-k=1时,q=2;
2)当n为偶数且k=3或k=n-3时,q为大于等于n-2的最小素数或素数的幂次;
3)其他情况下,q为大于等于n-1的最小素数或素数的幂次.
1.2 系统MSR码的结构及生成矩阵基于推论1,在最小有限域GF(q)中构造(n, k)系统MSR码. m=[m1 m2 …mk]为输入符号,c=[c1 c2 … cn]为系统MSR码的生成码字,且c=mGMSR,这里系统MSR码的生成矩阵GMSR=[I|P]k×n,其中I为k×k单位矩阵,P为k×(n-k)维子矩阵. (n, k)系统MSR码可表示为
| $ \boldsymbol{c} = \boldsymbol{m}{\boldsymbol{G}_{{\rm{MSR}}}}{\rm{ = }}\boldsymbol{m}{[\boldsymbol{I}{\rm{|}}\boldsymbol{P}]_{k \times n}} = [\boldsymbol{m}{\rm{|}}\boldsymbol{m}\boldsymbol{P}] $ |
根据Macwilliams[6]的结论,当矩阵GMSR=[I|P]k×n中子矩阵Pk×(n-k)任意子方阵都为非奇异矩阵时,GMSR中任意k列线性无关,满足MDS性质.考虑采用Vandermonde矩阵构造子矩阵Pk×(n-k),设α1, α2, …, αn-k为GF(q)中不包含0元素的n-k个元素,则系统MSR码的生成矩阵如定理2所示.
定理2 (n, k)系统MSR码的生成矩阵为
| $ \begin{array}{l} \begin{array}{l} {G_{{\rm{MSR}}}}{\rm{ = }}{[I{\rm{|}}P]_{k \times n}}{\rm{ = }}\\ \left[ {\begin{array}{*{20}{c}} 1&0&0& \cdots &0&0&1&1& \cdots &1\\ 0&1&0& \cdots &0&0&{{\alpha _1}}&{{\alpha _2}}& \cdots &{{\alpha _{n - k}}}\\ 0&0&1& \cdots &0&0&{\alpha _1^2}&{\alpha _2^2}& \cdots &{\alpha _{n - k}^2}\\ \vdots & \vdots & \vdots &{}& \vdots & \vdots & \vdots & \vdots &{}& \vdots \\ 0&0&0& \cdots &1&0&{\alpha _1^{k - 2}}&{\alpha _1^{k - 2}}& \cdots &{\alpha _{n - k}^{k - 2}}\\ 0&0&0& \cdots &0&1&{\alpha _1^{k - 1}}&{\alpha _2^{k - 1}}& \cdots &{\alpha _{n - k}^{k - 1}} \end{array}} \right] \end{array} \end{array} $ |
其中任意k列线性无关.
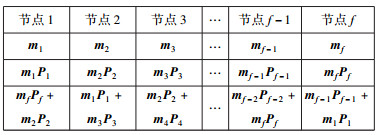
1.3 基于系统MSR码的局部性修复编码将(n, k)系统MSR码作为局部码,在具有f个云存储节点的修复组内构造局部性修复编码,确保MDS性质和简单修复特性,局部性修复编码的具体结构如图 1所示.
|
图 1 基于系统MSR码的局部性修复编码 |
考虑图 1中基于系统MSR码的局部性修复编码结构,每个节点存储的数据包含系统MSR编码数据和局部性修复编码生成的冗余数据.系统MSR编码数据的生成矩阵为
| $ \boldsymbol{G}{\rm{ = }}\left( \begin{array}{l} {\boldsymbol{G}_{{\rm{MSR\_1}}}}\\ \;\;\;\;\;\;\;\;\; \ddots \\ \;\;\;\;\;\;\;\;\;\;\;\;{\boldsymbol{G}_{{\rm{MSR}}\_f}} \end{array} \right) = \left( \begin{array}{l} \boldsymbol{I}{\rm{|}}{\boldsymbol{P}_1}\\ \;\;\;\;\;\; \ddots \ddots \\ \;\;\;\;\;\;\;\;\;\;\;\;\boldsymbol{I}{\rm{|}}{\boldsymbol{P}_f} \end{array} \right) $ |
其中GMSR_i=[I|Pi]k×n(i=1, 2, …, f).冗余数据生成矩阵为
| $ \boldsymbol{Q} = \left( {\begin{array}{*{20}{c}} \boldsymbol{0}&{{\boldsymbol{P}_1}}&\boldsymbol{0}& \cdots &\boldsymbol{0}&{{\boldsymbol{P}_1}}\\ {{\boldsymbol{P}_2}}&\boldsymbol{0}&{{\boldsymbol{P}_2}}& \cdots &\boldsymbol{0}&\boldsymbol{0}\\ \boldsymbol{0}&{{\boldsymbol{P}_3}}&\boldsymbol{0}& \cdots &\boldsymbol{0}&\boldsymbol{0}\\ \boldsymbol{0}&\boldsymbol{0}&{{\boldsymbol{P}_3}}& \cdots &\boldsymbol{0}&\boldsymbol{0}\\ \vdots & \vdots & \vdots &{}& \vdots & \vdots \\ \boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}& \cdots &{{\boldsymbol{P}_{f - 2}}}&\boldsymbol{0}\\ \boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}& \cdots &\boldsymbol{0}&{{\boldsymbol{P}_{f - 1}}}\\ {{\boldsymbol{P}_f}}&\boldsymbol{0}&\boldsymbol{0}& \cdots &{{\boldsymbol{P}_f}}&\boldsymbol{0} \end{array}} \right) $ |
根据图 1中基于系统MSR码的局部性修复编码结构,该局部性修复编码的编码率为k/(2n-k),小于系统MSR码的编码率为k/n,可见该局部性修复编码以较低的编码率为代价,换取对分布式存储系统中多个故障节点的高效快速修复.
2 故障节点快速修复算法为了保证DC在修复后的存储系统中采集数据不会增加额外磁盘I/O开销和带宽开销,考虑采用确定性修复,修复后新节点上恢复出的数据与故障节点原存储数据完全一致.下面从故障节点不相邻和相邻2种情况分别讨论故障节点的快速修复.
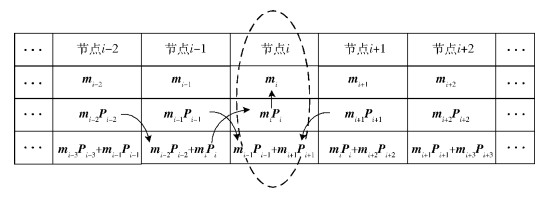
2.1 修复不相邻故障节点首先考虑分布式存储系统修复组内存在单节点故障的情况,如图 2所示.
|
图 2 修复组内单一故障节点修复 |
假定节点i(2≤i≤f-1)出现故障,可通过前后3个节点i-2、i-1和i+1重构节点i中的MSR编码数据miPi和冗余数据mi-1Pi-1+mi+1Pi+1.系统MSR编码数据的生成矩阵G已知,子矩阵GMSR_i确定,则该子矩阵GMSR_i中的Pi矩阵也确定.根据MSR编码数据miPi,可恢复出原始信息数据mi,实现故障节点i中的数据重构.同样地,也可采用节点i-1、i+1和i+2实现故障节点i中的数据重构.可以看出,在单节点故障情况下,基于系统MSR码的局部性修复编码,其修复局部性可达3.
进一步地,当分布式云存储系统修复组内多个不相邻节点同时发生故障,同样可采用上述方法进行故障节点修复.考虑到修复组内任意节点故障,需要前后共3个节点实现数据重构,且其中有2个节点还可参与到其他故障节点的数据重构,则存在f个节点的修复组,采用基于MSR码的局部性修复编码,最多可修复
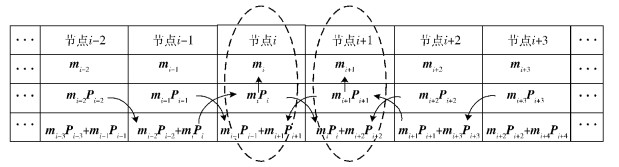
分布式存储系统修复组内2相邻节点故障的修复模型如图 3所示.对于故障节点i,可通过节点i-2和i-1,重构MSR编码数据miPi,进一步通过MSR编码矩阵GMSR_i,恢复信息数据mi;同样地,故障节点i+1通过节点i+2和i+3重构mi+1和mi+1Pi+1.在恢复出编码数据miPi和mi+1Pi+1的基础上,节点i和i+1相互利用对方MSR编码数据,以及相邻节点i-1和i+2上的编码数据mi-1Pi-1和mi+2Pi+2,恢复出冗余数据mi-1Pi-1+mi+1Pi+1和miPi+mi+2Pi+2,实现故障节点上的数据重构.
|
图 3 修复组内2相邻故障节点修复 |
上述故障节点修复算法可进一步扩展到修复组内存在多对2相邻节点故障的情况.考虑到修复组内2相邻节点发生故障,需要前后共4个节点实现数据重构,且这4个节点还可参与到其他故障节点的修复,则在具有f个节点的修复组中,基于MSR码的局部性修复编码进行故障节点修复,最多可修复
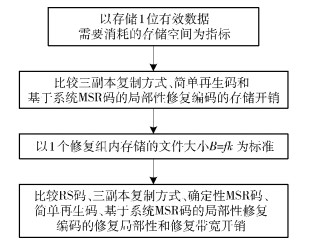
首先讨论基于系统MSR码的局部性修复编码方案的存储开销,并与最常用的三副本复制方式和最典型的局部性修复编码-简单再生码[3]进行对比;接下来,理论分析基于系统MSR码的局部性修复编码方案的修复局部性,进一步验证笔者提出的方案可获得较低的修复局部性;最后对提出方案的带宽开销进行分析,并分别与RS码、三副本复制方式、确定性MSR码、简单再生码进行对比.具体的实验流程如图 4所示.
|
图 4 实验流程 |
以存储1位有效数据需要消耗的存储空间作为衡量存储开销的指标,分别比较三副本复制方式、简单再生码[3]和基于系统MSR码的局部性修复编码的存储开销.三副本复制是实际分布式存储系统中最常用的副本复制方式,且三副本复制方式中存储1位有效数据,需要的存储空间为3位,即存储开销为3.
简单再生码通过将(n, k)RS码作为局部码,并在简单异或运算基础上构造生成,可对单节点故障实现高效修复.根据简单再生码的编码结构,容易得到简单再生码的存储开销为RS码存储开销的3/2倍,即α简单再生码=3n/2k.进一步地,根据图 1中基于系统MSR码的局部性修复编码的编码结构,节点i中存储数据mi、miPi和mi-1Pi-1+mi+1Pi+1,共需要n+(n-k)=2n-k位的存储空间,且节点i中存储的信息数据mi只有k位,则存储1位有效数据需要消耗的存储空间为(2n-k)/k,即存储开销为(2n-k)/k.
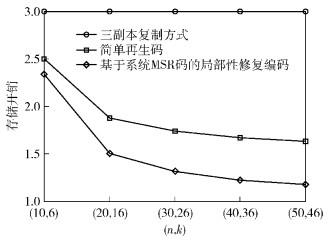
根据上述结论,容易得到不同(n, k)取值下,三副本复制方式、简单再生码和基于系统MSR码的局部性修复编码的存储开销,如图 5所示.固定n-k的值等于4,简单再生码和基于系统MSR码的局部性修复编码的存储开销都随着n值的增大而减小,远远小于三副本复制方式.对比简单再生码和基于系统MSR码的局部性修复编码,发现笔者提出方案的存储开销小于简单再生码.以(n, k)=(30, 26)为例,简单再生码的存储开销为1.731,而基于MSR码的局部性修复编码的存储开销为1.308,相对于简单再生码节约了24.4%的存储空间.可见,笔者提出的基于MSR码的局部性修复编码,在存储开销方面的性能优于三副本复制方式和局部性修复编码中的简单再生码.
|
图 5 3种方式下的存储开销对比 |
以基于系统MSR码的局部性修复编码1个修复组内存储的文件大小B=fk为标准,比较RS码、三副本复制方式、确定性MSR码、局部性修复编码中的简单再生码和基于系统MSR码的局部性修复编码的修复局部性.
具体地,将基于系统MSR码的局部性修复编码的参数n、k和f分别设置为n=30、k=26和f=8.分布式存储系统中若采用(n=30, k=26)RS码最多可修复n-k=4个故障节点,且实现故障节点修复时,至少需要连接k=26个存活节点,故(30, 26)RS码在修复1个或2个故障节点时,其修复局部性都为k=26.三副本复制方式的修复局部性最小,当1个存储节点发生故障,只需从其副本节点下载数据,便可实现故障节点修复,此时修复局部性为1;若存储系统中有2个节点同时发生故障,采用类似的方法,2个故障节点分别从其副本节点下载数据,实现故障节点修复,则2个节点故障时,三副本方式的修复局部性为2.
进一步地,考虑再生码中的确定性MSR码[7],修复故障节点需要从d≥2k-1个存活节点下载数据,则确定性(30, 26)MSR码的修复局部性的最小值为2k-1=51.局部性修复编码中的简单再生码在修复1个故障节点时,只需要连接4个存活节点,具有较低的修复局部性;若修复组内同时有2个节点故障,简单再生码此时需要连接k=26个存活节点进行修复,修复局部性为26.
笔者提出的基于系统MSR码的局部性修复编码,当修复组内存在单节点故障,可通过前后3个节点重构故障节点中的MSR编码数据和冗余数据,修复局部性为3.当修复组内2节点同时发生故障,这里考虑修复局部性较高的情况,2不相邻节点发生故障.采用基于系统MSR码的局部性修复编码实现故障节点快速修复,共需要连接5个节点,其修复局部性为5.
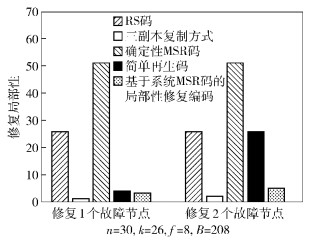
根据上述分析,得到对应的不同修复方式下的修复局部性,如图 6所示.容易看出,笔者提出的基于系统MSR码的局部性修复编码的修复局部性远远小于RS码和确定性MSR码,接近修复局部性较低的三副本复制方式.对比简单再生码和基于系统MSR码的局部性修复编码,修复1个故障节点时,两者的修复局部性比较接近;当修复组内同时有2个节点发生故障,简单再生码需要连接k=26个存活节点,修复局部性为26,而基于系统MSR码的局部性修复编码,此时只需要连接5个存活节点,其修复局部性明显小于简单再生码.
|
图 6 不同修复方式在n=30, k=26, f=8时的修复局部性 |
比较RS码、三副本复制方式、确定性MSR码、简单再生码和基于系统MSR码的局部性修复编码的修复带宽开销,同样如图 1所示基于系统MSR码的局部性修复编码1个修复组内存储的文件大小B=fk为标准.
首先考虑RS码,分布式存储系统若采用(n, k)RS码的修复方式,文件大小B=fk,则每个存储节点将存储B/k个数据.根据3.2小节修复局部性的分析,得到(n, k)RS码最多可修复n-k个故障节点,为实现故障节点修复,至少需要连接k个存活节点.
根据上述结论,容易得出(n, k)RS码在修复1个或2个故障节点时,修复带宽开销为(B/k)k=B.三副本复制方式通过在存储节点中存储原文件数据的另外2个副本,确保存储其中1个副本的节点发生故障时,可从另外2个副本节点读取数据,确保存储的可靠性.在三副本复制方式中,每个节点将存储3B/n个数据,当1个存储节点发生故障,只需从其中1个副本节点下载数据,修复带宽开销为3B/n;若存储系统中有2个节点同时发生故障,2个故障节点需要分别从其副本节点下载数据,修复带宽开销为6B/n.
MSR码在确保分布式存储系统节点存储开销最小的同时,其修复带宽开销为γMSR=Bd/k(d-k+1)[8],故确定性MSR码在修复1个或2个故障节点时的修复带宽开销都为Bd/k(d-k+1).在简单再生码中,每个分布式存储节点中存储3B/2k个数据,其在修复1个故障节点时,需要连接4个存活节点,且从其中2个节点分别下载B/2k个数据,从另外2个节点分别下载B/k个数据,则修复带宽开销为2(B/2k+B/k)=3B/k;当存储系统中有2个节点发生故障,采用简单再生码进行故障节点的数据重构,需要连接k个存活节点,此时数据重构过程同RS码,则修复带宽开销也为B.
基于系统MSR码的局部性修复编码,若修复组内存在1个故障节点,需要连接前后共3个节点实现数据重构,如图 2所示.假定节点i(2≤i≤f-1)出现故障,采用图 2中的故障节点修复方案,需要从节点i-2和i+1分别下载mi-2Pi-2和mi+1Pi+1,从节点i-1中下载数据mi-1Pi-1和mi-2Pi-2+miPi,共4(n-k)个数据,修复带宽开销为4(n-k).同理,对于修复组内存在2个故障节点的情况,可采用图 3中的方案进行故障节点修复,修复每个节点的带宽开销为4(n-k),则修复2个故障节点总的修复带宽开销为8(n-k).
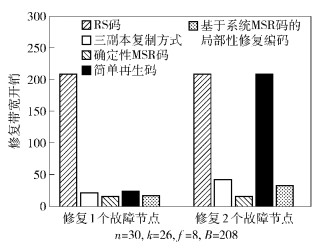
根据上述分析,总结不同修复方式下的修复带宽开销,如表 1所示.具体地,在此将参数n、k和f同样设置为n=30、k=26和f=8,B=fk=208.在此参数下,可分别得到修复1个故障节点和2个故障节点时,RS码、三副本复制方式、确定性MSR码、简单再生码和基于系统MSR码的局部性修复编码的修复带宽开销,如图 7所示.容易看出,基于系统MSR码的局部性修复编码的修复带宽开销远远小于RS码,且略小于三副本复制方式.对比简单再生码和基于系统MSR码的局部性修复编码,修复1个故障节点时,简单再生码的修复带宽开销略高于基于系统MSR码的局部性修复编码;当修复组内同时有2个节点发生故障,简单再生码进行2个故障节点的数据重构,需要连接k个存活节点,此时数据重构过程同RS码,则修复带宽开销为B,远远高于基于系统MSR码的局部性修复编码.进一步地,确定性MSR码在修复1个或2个故障节点时的修复带宽开销都为Bd/k(d-k+1),对比分析发现,基于系统MSR码的局部性修复编码的修复带宽开销略大于确定性MSR码.
|
图 7 不同修复方式在n=30, k=26, f=8时的修复带宽开销 |
|
|
表 1 不同修复方式下的修复带宽开销 |
现有的局部性修复编码方案只能实现少数故障节点的快速修复,无法保证对多个故障节点进行快速修复,也没有考虑节点的存储开销.为此,笔者提出一种基于MSR码的局部性修复编码方案,在分布式云存储系统中采用系统MSR码,云存储节点存放原始数据副本.将构造的系统MSR码作为局部码,构造局部性修复编码,确保MDS性质和简单修复特性,实现修复组内故障节点的快速修复.性能分析和实验仿真表明,该局部性修复编码方案在存储开销方面的性能优于三副本复制方式和简单再生码,修复局部性接近修复局部性较低的三副本复制方式;相对于RS码、三副本复制方式和简单再生码,该局部性修复编码方案在修复带宽开销方面的性能更优.
| [1] | Acedanski S, Deb S, Medard M, et al. How good is random linear coding based distributed networked storage?[C]//Proc of 1st Workshop on Network Coding, Theory and Applications(NetCod).[s.l.]:IEEE, 2005:1-4. |
| [2] | Dimakis A G, Godfrey P B, Wainwright M J, et al. Network coding for distributed storage systems[C]//26th IEEE International Conference on Computer Communications(INFOCOM 2007).[s.l.]:IEEE, 2007:2000-2008. |
| [3] | Papailiopoulos D S, Dimakis A G. Locally repairable codes[J]. IEEE Transactions on Information Theory , 2014, 60 (10) :5843–5855. doi:10.1109/TIT.2014.2325570 |
| [4] | Shahabinejad M, Khabbazian M, Ardakani M. An efficient binary locally repairable code for hadoop distributed file system[J]. IEEE Communications Letters , 2014, 18 (8) :1287–1290. doi:10.1109/LCOMM.2014.2332491 |
| [5] | Goparaju S, Calderbank R. Binary cyclic codes that are locally repairable[C]//2014 IEEE International Symposium on Information Theory(ISIT).[s.l.]:IEEE, 2014:676-680. |
| [6] | Macwilliams F J, Sloane N J A. The theory of error correcting codes[M]. Netherlands: North-Holland Mathematical Library , 1983 . |
| [7] | Changho S, Kannan R. Exact-repair MDS code construction using interference alignment[J]. IEEE Transactions on Information Theory , 2011, 57 (3) :1425–1442. doi:10.1109/TIT.2011.2105003 |
| [8] | Ernvall T. Exact-regenerating codes between MBR and MSR points[C]//2013 IEEE Information Theory Workshop(ITW).[s.l.]:IEEE, 2013:1-5. |


