2. 食品安全大数据技术北京市重点实验室, 北京 100048 ;
3. 北京邮电大学 计算机学院, 北京 100876
针对光场描述符丢失三维模型空间信息以及全景视图描述符投影视图较少的问题,提出一种结合深度图像的三维模型检索算法.该算法引入深度图像对光场描述符加以改进,得到投影视图后,分别提取其离散小波变换特征和Zernike矩特征;然后对深度图像进行聚类去掉冗余信息,并通过随机游走算法来确定每一类的权重,以更好地反映类间关系;最后设计改进全景视图相似距离计算方法,用于进一步的三维模型检索.在普林斯顿模型库上的实验结果表明,该算法有效利用了三维模型空间信息,提高了检索精确度.
2. Beijing Key Laboratory of Big Data Technology for Food Safety, Beijing 100048, China ;
3. School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China
Due to the problem of light field descriptor lacking spatial information of 3D model, and the problem of little projection of PANORAMA descriptor, a 3D model retrieval algorithm combining depth image was proposed. The depth images are used to improve light field descriptor. Discrete wavelet transform features and Zernike moments are extracted from projection views. Then the depth images are clustered to remove redundancy. The random walk algorithm is employed to determine the weight of each cluster. Finally, the retrieval method of PANORAMA is optimized to calculate similarity distance between two 3D models. Results on princeton shape benchmark show that the proposed algorithm can make good use of spatial information of 3D model and improve the accuracy of retrieval.
目前,三维模型广泛地应用在许多不同的领域中,如机械制造、考古、医学、游戏、计算机视觉等,如何在海量三维模型中,高效准确地检索所需要的模型,提高模型的复用率,已经成为一个重要的研究方向[1].
近年来,基于视图的三维模型检索成为一个新的研究热点.由于基于视图的检索方法利用一幅或多幅图像对三维模型进行表示,这些图像可以由特定的相机序列或者虚拟相机序列获得,使得这种表达方式具有很强的识别度[1].基于视图的方法分为投影方法、视图学习方法两类.
投影方法[2-3]:此类方法通过投影获得三维模型的二维信息,但是没有充分学习视图间关系,检索精确度有待进一步提高.
视图学习方法[4-5]:此类方法通过学习视图间关系,提高了检索精确度,但是只提取了二维图像单一特征,不能充分表达三维模型信息.
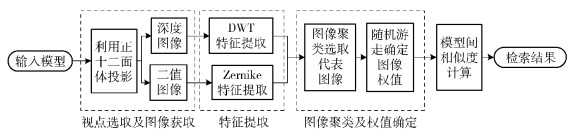
1 算法描述针对以上方法的问题,笔者将光场描述符(LFD, light field descriptor)[2]和全景视图描述符(PANORAMA)[3]这2种方法结合,并引入空间深度信息,提出一种结合深度图像的三维模型检索方法.在投影阶段,本方法利用LFD的投影方式进行深度图像和二值图像投影,获取模型空间和轮廓信息;在图像聚类减少信息冗余后,引入随机游走算法进行图像权值确定;最后设计改进PANORAMA相似度距离计算方法并进行模型间相似度计算.算法流程如图 1所示.
|
图 1 算法流程 |
本算法采用LFD投影方式,如图 2所示,10个正十二面体交错作为外包围盒的投影方式,但不同的是将正十二面体的20个顶点都作为视点,进行三维模型投影.在投影之前,首先将三维模型进行归一化,以确保投影视图尺寸一致.每幅深度图像和二值图像的尺度为N×N,取N=256. 图 3为模型投影的部分结果.

|
图 2 LFD投影方法 |

|
图 3 动物模型部分投影示例图 |
1)深度图像离散小波变换(DWT, discrete wavelet transform)特征提取:对每一幅图像进行二维DWT[6],并将其系数做如式(1)和式(2)所示的处理作为本幅图像特征.
| $ W_{k, t}^\phi ({j_0}, m, n) = \frac{1}{N}\sum\limits_{u = 0}^{N-1} {\sum\limits_{v = 0}^{N-1} {{s_{k, t}}({\phi _u}, {y_v}){\phi _{{j_0}, m, n}}(u, v)} } $ | (1) |
| $ W_{k, t}^\psi (j, m, n) = \frac{1}{N}\sum\limits_{u = 0}^{N-1} {\sum\limits_{v = 0}^{N-1} {{s_{k, t}}({\phi _u}, {y_v}){\psi _{j, m, n}}(u, v)} } $ | (2) |
其中:m, n∈[0, N-1];j≥j0为多层DWT的尺度,j0=0;sk, t(Φu, yv)代表投影视图;Φj0, m, n(u, v)和ψj, m, n(u, v)分别为不同的小波方程;Wk, tφ(j0, m, n)为在尺度j0下,近似低频系数;Wk, tψ(j, m, n)为在尺度j下,小波的高频系数,共包括垂直、水平、对角3个方向.采用哈尔(Harr)小波进行图像特征提取.
由于图像尺度为N×N,所以提取lbN层小波变换系数,其中j=0, 1, 2, …, log2N-1.对每幅图像进行小波变换后,共可以得到N×N个小波系数.为了提高计算效率,简化特征向量,对小波低频系数和每层高频系数的3个方向分别提取平均值、标准差、偏度作为进一步的特征表示,共75维.
2)二值图像Zernike矩特征提取:Zernike矩具有旋转不变性等优点,本方法中,对每一幅二值图像进行49维Zernike矩特征提取.对尺度为N×M的图像提取(s+t)维Zernike,可定义为
| $ {Z_{st}} = \frac{{s + 1}}{t}\sum\limits_{x = 0}^{N-1} {\sum\limits_{y = 0}^{M-1} {f(x, f){P_{st}}(x, y)} } $ | (3) |
其中Pst(x, y)定义为
| $ {P_{st}}(x,y) = {P_{st}}(\rho ,\theta ) = {R_{st}}(\rho ){\rm{exp}}(\widehat {\rm{j}}t\theta ) $ | (4) |
其中Rst(ρ)为实值径向多项式.
1.3 图像聚类及权值确定每个三维模型由多幅深度图像和二值图像表示.图像中包含了大量的冗余信息.为了进一步学习视图间关系提高检索效率,降低计算复杂度,引入k-means算法,利用DWT特征将图像聚成10类,并选取离聚类中心欧氏距离较近的深度图像和相对应的二值图像作为此类的代表图像.
聚类完成后,为每个代表图像赋予不同的权值.每个代表图像的初始权值τ(0)设定为
| $ \tau _i^{(0)} = \frac{{\left| {C(i)} \right|}}{Q}, i = 1, 2, \cdots, 10 $ | (5) |
其中:|C(i)|为第i类中图像的数量,Q为总的图像数量.
为了更好地展现出每个代表图像之间的关系,利用随机游走算法来进行进一步的权值调整.第i和第j幅代表图像的相似性si, j定义为
| $ {s_{i, j}} = \exp \left( {-\frac{{d({v_i}, {v_j})}}{\sigma }} \right) $ | (6) |
其中:d(vi, vj)为第i和第j幅代表图像的欧氏距离,σ为10幅代表图像间距离的标准差.
第i和第j幅代表图像的转化概率定义为
| $ {P_{i, j}} = \frac{{{s_{i, j}}}}{{\sum\limits_{k \ne i} {{s_{i, k}}} }} $ | (7) |
随机游走迭代过程为
| $ \tau _i^{(t + 1)} = \alpha \sum\limits_{k \ne i} {\tau _k^{(t)}{p_{k, i}} + (1-\alpha )} \tau _i^{(0)} $ | (8) |
直到每个权值稳定.其中α为一个常数,实验中设定为0.5.经过随机游走过程后,就为每个代表图像确定了合适的权值.
1.4 模型间相似度计算此时每个三维模型由10类具有不同权重的深度图像和二值图像表示. 2个模型O1、O2间相似距离可定义为
| $ d({O_1}, {O_2}) = \sum\limits_{i = 1}^n {d({v_{1i}}, v_{2i}^ \times ) = \sum\limits_{i = 1}^n {({f_{1i}}-f_{2i}^ \times )} } $ | (9) |
其中:d(v1i, v2i×)为模型O1中第i(1≤i≤10)类图像v1i与模型O2中最佳匹配的第i类图像v2i×的相似距离,f1i、f2i×分别为图像v1i和v2i×的特征向量元素.利用匈牙利算法进行二分图匹配,计算模型间的最小相似距离.其中2类图像间的距离d(v1i, v2i×)定义为
| $ d({v_{1i}}, v_{2i}^ \times ) = {w_{1i}}w_{2i}^ \times (\beta T({v_{1i}}, v_{2i}^ \times ) + \lambda Z({v_{1i}}, v_{2i}^ \times )) $ | (10) |
其中:w1i、w2i×分别为图像v1i和v2i×的权重;T(v1i, v2i×)、Z(v1i, v2i×)分别为2类图像标准化后的DWT和Zernike矩特征的距离,对T(v1i, v2i×)取兰氏距离,对Z(v1i, v2i×)取欧氏距离;β、λ分别为T(v1i, v2i×)和Z(v1i, v2i×)的权重,取β=0.89、λ=0.11.
2 实验与评估所提算法采用Matlab和C混合编程实现,程序的PC运行环境:CPU为Intel ® Xeon® E5620@2.40 GHz,内存为12.00 GB,操作系统为Windows 7 64位.
2.1 实验数据集及评价指标实验数据集为普林斯顿综合模型库,使用在SHREC[7]比赛中广泛采用的查全率-查准率曲线(PR, precision-recall)曲线、最近邻(NN, nearest neighbour)、第1层级(FT, first-tier)、第2层级(ST, second-tier)、F度量(F, F-measure)、折扣增益(DCG, discounted cumulative gain)等指标作为三维模型检索结果的评价标准.
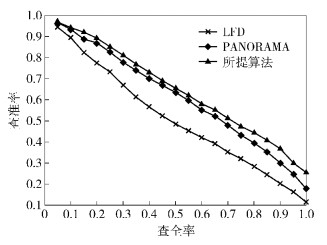
2.2 实验结果及其分析实验中将所提算法与原有算法LFD、PANORAMA进行比较. 表 1为3种算法的5种指标对比. 图 4为3种算法的PR曲线对比.
|
图 4 3种算法的PR曲线对比 |
|
|
表 1 3种算法5种指标(NN、FT、ST、F、DCG)对比 |
由图 4和表 2可看出,与LFD、PANORAMA相比,所提算法取得了较好的检索精确度.由实验结果可以看出,所提算法利用正十二面体获取三维模型的深度及轮廓信息,有效地弥补了LFD、PANORAMA获取模型信息不足的缺点;同时在特征匹配阶段,改进PANORAMA算法进一步提高了检索精确度.
|
|
表 2 3种算法5种模型输入相似度前5的检索结果 |
为解决LFD缺少三维模型空间信息等问题,提出一种结合深度图像的三维模型检索算法.该算法分别提取了投影图像的DWT特征和Zernike矩特征,进而通过聚类减少信息冗余,再利用随机游走来进一步挖掘代表图像的关系.与LFD、PANORAMA相比,该算法效果良好.下一步工作将结合外围球或者人眼成像透视法等投影技术提高三维模型检索的精度和效率.
| [1] | Gao Yue, Dai Qionghai. View-based 3D object retrieval:challenges and approaches[J]. IEEE Mutimedia , 2014, 21 (3) :52–57. doi:10.1109/MMUL.2014.20 |
| [2] | Chen Dingyun, Tian Xiaopei, Shen Yute, et al. On visual similarity based 3D model retrieva[J]. Computer Graphics Forum , 2003, 22 (3) :223–232. doi:10.1111/cgf.2003.22.issue-3 |
| [3] | Papadakis P, Pratikakis I, Theoharis T, et al. PANORAMA:a 3D shape descriptor based on panoramic views for unsupervised 3D object retrieval[J]. International Journal of Computer Vision , 2010, 89 (2-3) :177–192. doi:10.1007/s11263-009-0281-6 |
| [4] | Gao Yue, Wang Meng, Zha Zhengjun, et al. Less is more:efficient 3D object retrieval with query view selection[J]. IEEE Transactions on Multimedia , 2011, 13 (5) :1007–1018. doi:10.1109/TMM.2011.2160619 |
| [5] | Lu Ke, He Ning, Xue Jian, et al. Learning view-model joint relevance for 3D object retrieval[J]. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society , 2015, 24 (5) :1449–1459. doi:10.1109/TIP.2015.2395961 |
| [6] | 余先川. 基于小波变换和稀疏成分分析的盲图像分离法[J]. 北京邮电大学学报 , 2010, 33 (2) :58–63. Yu Xianchuan. Blind image separation based on wavelet transformation and sparse component analysis[J]. Journal of Beijing University of Posts and Telecommunications , 2010, 33 (2) :58–63. |
| [7] | Gao Yue, Liu Anan, Nie Weizhi, et al. 3D object retrieval with multimodal views[C]//Proceedings of the 2015 Eurographics Workshop on 3D Object Retrieval. Eurographics Association, 2015:129-136. |








