2. 中国联合网络通信有限公司, 北京 100033
针对已有的软件定义网络(SDN)控制器部署关注基于控制消息路由时延最优的问题,引入节点的介数中心性作为参数,分析了介数中心性对于控制器部署位置选择的重要性,并联合节点的可靠性提出了一种基于多参数节点排序方案(MFRS)的控制器位置部署策略,将节点进行排序并分层,依据节点间的连接关系计算出控制权值,最终确定控制器位置.仿真结果表明,MFRS的控制消息路由跳数小于基于时延的最短路径算法,且基于MFRS的网络可靠性高于基于时延的最短路径算法.
2. China United Network Communications Company Limited, Beijing 100033, China
Current research on controller deployment in software-defined network(SDN) mainly focuses on latency optimal of the controlling messages routing. The betweenness centrality was introduced as a factor to the controller deployment problem and the importance of betweenness centrality in controller deployment location was analyzed. Then a multi-factor node ranking scheme(MFRS) was proposed, the betweenness and the reliability are chosen for the node ranking factors. The nodes are layered and the controlling weight of each node was calculated according to the connecting relations of the nodes in different layers. The location of the controller was determined finally. Simulation shows that the hops of the controlling messages routing under MFRS is less than under the latency aware shortest path scheme, and the reliability of MFRS is higher than it of the latency aware shortest path scheme.
软件定义网络(SDN, software-defined network)是一种可编程集中控制的新型网络架构,跨区域的大型网络中也开始部署SDN架构.现有研究多数基于SDN控制平面网络和数据平面网络在物理上独立组网的模式,而跨区域大型网络建设中单独建立控制平面网络成本巨大.因此,SDN实际部署往往采用控制平面和数据平面共享物理网络的模式来降低成本.所以,控制器的部署位置选择也成为了关注的焦点.笔者为了寻找一个最佳的控制器位置,优化控制节点的可靠性以及控制消息的路由时延,引入介数中心性,提出了基于多参数节点排序方案(MFRS, multi-factor node ranking scheme)的控制器部署算法,并通过仿真验证其性能.
1 问题描述控制器的位置对SDN的性能可以产生重要影响.Heller等[1]讨论了在关注时延的网络中控制器数量以及控制器部署位置;Hu等[2]从可靠性的角度对SDN中控制器的部署进行了分析;Yao等[3]提出了一种基于传输时延和发送时延的网络快速响应控制器部署方案;Stanislav等[4]从网络弹性角度出发基于Pareto最优设计了启发式的控制器放置算法.控制器承担着对SDN中流的转发控制任务,当网络中任意两点产生新的流时,沿途节点将会询问控制器该条流将如何转发,并收到来自控制器的控制消息,而控制消息每往复一次所经过的跳数或时延是控制器性能体现的关键因素.假设到每一节点的控制消息都需从控制器出发,设节点n1, nk间的最短路径为path(n1, nk),从n1到nk共k个节点,如图 1(a)所示.当控制器v的位置处于path(n1, nk)上时,控制消息经历的跳数h取值范围是[hmax, hmin].其中,hmax=k!(v=n1或nk),此时v处于路径的两端;
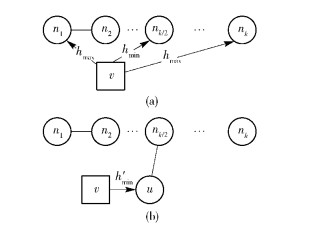
|
图 1 控制器位置对控制消息跳数的影响 |
所以控制器的部署节点越靠近网络中心,越有利于控制消息的快速转发,节点的中心性评估显得尤为重要.网络节点的中心性分为度中心性、介数中心性、紧密中心性等,介数中心性是用来描述节点在网络中的重要性的一个度量,源于复杂网络领域,衡量通过某节点的所有最短路径的数量,以确定网络节点的中心性.设网络无向图G(V, E),其中V为节点集,E为边集,任意两节点s、t∈V,Lst=Lts表示节点s与节点t之间最短路径的数量, Lst(v)表示节点s与节点t之间经过节点v的最短路径的数量.网络G(V, E)中节点v的介数中心性定义为[5]
| $ B\left(v \right)=\sum\limits_{s\ne v\ne t\ne V}{\frac{{{L}_{st}}\left(v \right)}{{{L}_{st}}}} $ | (1) |
在基于最短路径路由的网络中,介数越大,节点在网络的中心度越高,意味着将控制更多的流(信息、资源等),控制器在此节点上的流表操作更频繁.因此,基于集中控制的SDN更适合在此类节点上部署控制器,以提高流表操作的效率.所以控制器节点的介数中心性在SDN中又可以体现此节点需要承担的流表操作的任务量,在介数大的节点上部署控制器将会节省控制消息的路由开销.因此,介数中心性与控制消息转发效率是一致的.
节点可靠性是又一个重要的评价标准,节点可靠性是在一定时间内处于正常工作状态时长比例,可按照一定的周期计算获得,并以归一化的数值表示节点可靠性.由于控制器是SDN的核心,所以控制器所在的节点一定要拥有更高的可靠性,以保证控制消息顺利到达其他节点.
如图 2所示,节点的介数和可靠性表示为(B,R),每个节点的参数如图中标记,假设网络中需要部署1个控制器.如果按照节点的介数对节点进行排序,控制器应当设置在节点c,因为节点c的介数最大,也就是网络中心性最强的节点,将可以控制更多的最短路径,因此,控制消息下发的任务量应该最小,但是可以看到,此节点的可靠性并不是最高的,繁重的任务也导致了节点故障的概率增加.如果控制节点发生了故障,或者某一个端口发生了故障,网络控制受到的影响也应该是最大的.如果将节点按照可靠性排序,控制器应部署在e节点,但是控制器的中心性明显不足,控制的最短路径数目不是最优的,增加了控制消息路由的任务量.通过上述分析可以得出:①控制器位置对控制消息平均时延以及控制消息路由树性能产生影响;②节点介数中心性最大和可靠性最大两个性能指标同时满足的概率较低,这是因为两个性能指标间相互独立,且有时存在冲突.
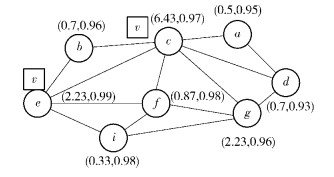
|
图 2 示例网络拓扑及相关参数 |
综上,SDN的控制器部署位置问题可以总结为如何选择既处于中心位置又有高可靠性的节点来部署SDN控制器.
2 基于MFRS的控制器部署目前的研究主要集中在针对控制消息的网络延时来优化控制器的位置,未考虑其他的诸多因素,有的研究考虑了诸如延时和可靠性[6],却忽略了节点的中心性.针对该问题,提出了一种基于MFRS的控制器部署算法,该算法同时考虑节点的介数中心性以及节点可靠性之间的均衡,并采用一种综合指标来衡量节点控制器部署的优劣程度.
Pei等[6]定义了一种节点多维参数间的支配关系,并基于这种支配关系建立了节点的分层方法以及支配权值的算法,以便得到节点在某种角度下的优劣程度.该算法在支配权值的计算只考虑了节点参数间的支配关系,并没有将节点间的连接关系考虑到其中,笔者在此基础上,设计了一种基于连接关系的控制权值计算方法,充分考虑到即使在多维参数之间不存在支配关系的节点间也是可以相互影响的事实,将节点间的距离作为连接关系的体现,得到控制器部署算法.
支配关系[7]:多维数组集合
基于支配关系将节点分层,通过比较节点的参数支配关系,得到一种按照综合因素的节点分层结果,设节点只能被第1~k层节点所支配,则该节点属于第k+1层;特别地,当一个节点不被任何节点所支配时,那么将此节点作为第1层节点.目的是从处于第1层的节点中选择一个节点来部署SDN控制器,在这种分层算法中,第1层通常会有多个节点,定义一个节点控制权值来衡量在同一层的节点的优劣,以便选择出最优控制器部署节点.
层次衰减系数α:在网络中,按照上述分层方法,第M+1层节点v处于第M层节点u的低一层,且在网络中v到u最小跳数为h,那么称v对于u的层次衰减系数为α(u, v)=1/h.
节点u的控制权值Cu:设节点u处于网络节点分层的第M层,那么此节点的控制权值为第M+1层中所有节点的层次衰减系数乘以其本身权值后求和.如果节点处于最底层,则此节点自然控制权值为0.1;特殊地,为了便于计算,在次底层计算对底层节点的控制权值时,底层节点的计算权值设置为1.例如,第M+1层有节点(v1, v2, …, vn),到节点u的最短跳数分别为(h1, h2, …, hn),则
| $ {{C}_{u}}=\sum\limits_{i\in \left[1, n \right]}{{{C}_{{{v}_{i}}}}{{\alpha }_{\left(u, {{u}_{i}} \right)}}=}\sum\limits_{i\in \left[1, n \right]}{\frac{{{C}_{{{v}_{i}}}}}{{{h}_{i}}}} $ | (2) |
控制权值是用于表明该模型中同层节点优劣性的指标,控制权值越大的节点越优.
假设控制器位置可以部署在全网的任何交换机位置上,且忽略控制器到其所在节点间的时延;控制器与交换机间只存在一条可用路径,这是由于控制平面采用传统二层的转发机制,需确保控制平面拓扑无环路[7].多参数节点选择算法如下:
输入:节点介数和可靠性(Bu,Ru)
输出:所有节点的控制权值Cu
第1步:根据网络拓扑计算所有节点的介数Bu;计算所有节点的可靠性Ru.
第2步:判断节点间的支配关系.
第3步:对节点按支配关系进行分层.
第4步:计算最底层节点的控制权值;利用第M+1层的结果来计算第M层节点的控制权值,直至输出第1层所有节点的控制权值.
第5步:选择第1层中最高权值的节点作为控制器节点.
如图 2所示的网络,介数和可靠性已经计算完成,其中各个节点的支配关系如表 1所示.按照MFRS进行分层得到如图 3所示的结果,连接相邻两层之间的连线上的数字为节点间的层次衰减系数,顶层节点为c和e.自底层向上计算顶层节点的控制权值,Cc=55/24,Ce=50/24 < Cc,所以,控制器应当部署在节点c上.
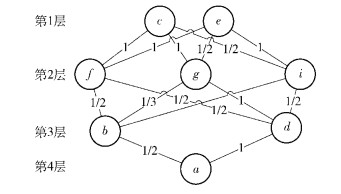
|
图 3 节点分层结果 |
|
|
表 1 节点分层及控制权值的计算 |
在C++平台上模拟了MFRS以及关注时延的最短路径(latency-SP, latency-shortest path)算法,对比了在相同条件下两种算法的控制平面网络可靠性以及控制消息到达各个节点的总时延.仿真拓扑分别为10节点的Internet2网络拓扑和20节点的随机拓扑,节点的可靠性在[0.95, 1)之间随机分布,两节点间的时延以控制消息路由跳数衡量,控制消息路由跳数定义为从控制器所在节点到各个节点的最短跳数总和.网络的可靠性指标定义为以控制器所在节点到各个节点的最短路径上节点的可靠性数值乘积.
如图 4(a)所示,在MFRS中,根据节点的控制权值曲线显示,应该在节点9上部署控制器,此时产生的控制消息路由跳数为16;而按照latency-SP算法,控制器的节点应该设置在其控制消息路由跳数最低的节点上,可以看出,部署在节点4上,该算法的跳数最低为19.同理,图 4(b)给出了节点数量更多的拓扑中两种算法的性能比较,可以看出,MFRS中控制权值高的节点11仍然是控制消息路由总跳数最低(34跳)的控制器部署位置,节点7则是latency-SP算法中控制消息路由总跳数最低(46跳)的.总之,在两种网络拓扑中,MFRS中所有的控制器位置产生的路由跳数少于latency-SP算法,且在控制权值较高的节点上均出现了路由跳数的较低值.这说明,控制器部署节点的介数中心性确实可以影响网络控制消息的转发性能,而由所提的节点分层方法计算的控制权值在控制节点选择中也是起到了应有的作用.而且,MFRS在拓扑发生变化时依然有效.
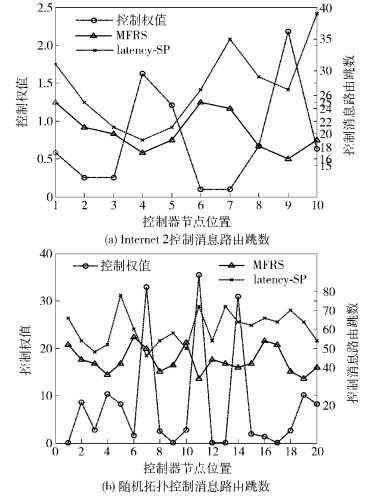
|
图 4 控制消息路由跳数 |
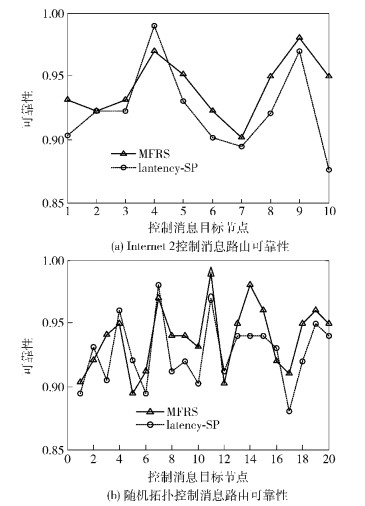
基于上述控制器位置得到两种网络拓扑下的控制消息路由可靠性的比较如图 5所示,MFRS总体上优于latency-SP算法.由图 5(a)可以看出,latency-SP算法中除控制器所在节点本身的可靠性高于MFRS外(此时控制消息路由可靠性为节点本身可靠性值,没有路径上其他节点的可靠性乘积衰减),到达剩余节点的控制消息路由可靠性均低于MFRS.这说明,在MFRS中将节点可靠性作为算法参数可以有效地提高控制消息路由的可靠性.而图 5(b)中,latency-SP算法的可靠性高于MFRS的情况略多,这是因为并不是MFRS中控制器到所有节点的控制消息路由路径的跳数都小于latency-SP算法,MFRS中有少数节点的控制消息路由跳数大于或等于latency-SP算法,可能出现在latency-SP算法控制器所在节点本身和到相邻节点的路径等情况中,最短路径上的节点数量少,控制消息路由可靠性乘积衰减减少,从而出现上述现象.但是绝大多数情况下的MFRS可靠性都优于latency-SP算法,这也说明,在节点数量变化时,MFRS仍然可以发挥重要作用.
|
图 5 控制消息路由可靠性 |
控制器部署位置问题是当前SDN领域中的研究热点,笔者引入节点的介数中心性作为衡量控制器部署问题的重要指标,分析了节点介数中心性在网络中的作用以及对SDN控制器位置部署方面的影响,提出了一种节点介数中心性和可靠性联合优化的MFRS控制器部署算法,设计了节点排序和选择的规则,并进行了仿真对比.仿真结果表明,MFRS可以在控制消息路由跳数、可靠性等指标性能上取得较其他算法更优的效果.
| [1] | Heller B, Sherwood R, McKeown N. The controller placement problem[C]//The First ACM SIGCOMM Workshop on Hot Topics in Software Defined Networking. 2012:7-12. |
| [2] | Hu Yanan, Wang Wendong, Gong Xiangyang, et al. Reliability-aware controller placement for software-defined networks[C]//2013 IFIP/IEEE International Symposium on Integrated Network Management. 2013:672-675. |
| [3] | Yao Linyuan, Chen Ying, Song Fei, et al. Delay-aware controller placement for fast response in software-defined network[J]. Journal of Electronics & Information Technology , 2014, 36 (12) :2802–2808. |
| [4] | Stanislav L, Steffen G, Thomas Z, et al. Heuristic approaches to the controller placement problem in large scale SDN networks[J]. IEEE Transactions on Network and Service Management , 2015, 12 (1) :4–17. doi:10.1109/TNSM.2015.2402432 |
| [5] | He Yu, Zhao Hongli, Yao Yao, et al. An integrated approximation algorithm for the betweenness centrality and average shortest path length[J]. Complex Systems and Complexity Science , 2011, 8 (3) :44–53. |
| [6] | Pei Jian, Jiang Bin, Lin Xuemei, et al. Probabilistic skylines on uncertain data[C]//Proceedings of the 33rd International Conference on Very large Data Bases. 2007:15-26. |
| [7] | 王健, 黄韬, 谢人超. 启发式构建软件定义网络的控制消息路由树算法[J]. 北京邮电大学学报 , 2015, 38 (3) :82–87. Wang Jian, Huang Tao, Xie Renchao. A heuristic algorithm for constructing control-traffic routing tree in software-defined networks[J]. Journal of Beijing University of Posts and Telecommunications , 2015, 38 (3) :82–87. |


