为了改善概率矩阵分解模型进行学术论文推荐时存在的数据稀疏性和冷启动问题,提出了一种混合推荐模型--主题矩阵分解模型.通过提出的作者-会议-时间-主题模型和传统的潜在狄利克雷分布主题模型分别构建用户和论文的主题特征,并通过这2类特征分别增强概率矩阵分解模型的用户潜在因子特征向量和项目潜在因子特征向量.实验结果表明,该模型较好地解决了概率矩阵分解模型的数据稀疏性问题和冷启动问题,有效提升了学术论文的推荐效果.
The inherent data sparsity and cold start problems in probabilistic matrix factorization(PMF) limit the effect of academic paper recommender. To remedy the shortcomings and enhance the recommender effect, a new hybrid recommender model named as matrix factorization with topic(MFWT) was proposed. The model constructs topic characteristics of both users and papers using the author-conference-topic over time(ACTOT) model and the traditional latent dirichlet allocation topic model respectively, enhancing the corresponding user and paper latent factor characteristic vectors of PMF model. Experiments show that the model well overcomes the data sparsity problem and the cold start problem of PMF and increases the effect of academic paper recommender.
矩阵分解模型具有简单高效的特点,其中的潜在因子模型(LMF,latent factor model)[1]和概率矩阵分解(PMF,probabilistic matrix factorization)[2]被广泛采用.但仍然没有解决基于协同过滤的推荐系统普遍存在的数据稀疏性和项目冷启动问题.
为改善协同过滤评分矩阵的数据稀疏性问题,Guo等[3]提出了信任关系强度敏感的社会化推荐算法.Fang等[4]提出了基于标签迁移学习的推荐算法.Guo等[5]提出了结合推荐项目间关联关系的推荐算法.Jiang等[6]则结合用户评论信息来解决协同过滤评分矩阵的稀疏性问题.但上述方法不能很好地处理文本信息,不能满足学术论文推荐对文本对象的处理需求.Wang等[8]将协同过滤推荐和基于内容的推荐相结合,提出协同主题回归(CTR,collaborative topic regression)模型,通过潜在狄利克雷分布(LDA,latent dirichlet allocation)对PMF的项目潜在因子特征向量进行增强,消除了PMF存在的冷启动问题,但其仍没有解决PMF的数据稀疏性问题.
为了同时解决PMF存在的项目冷启动问题和用户数据稀疏性问题,笔者在CTR基础上提出了主题矩阵分解模型(MFWT,matrix factorization with topic).该模型基于笔者提出的作者-会议-时间-主题(ACTOT,author-conference-topic over time)模型,对PMF中的用户潜在因子特征向量进行正则化处理,同时使用LDA模型计算的论文主题向量对PMF中的项目潜在因子特征向量作正则化处理.
1 ACTOT模型用户查阅学术论文时主要关注论文内容、论文发表的会议/期刊和发表时间等,因此笔者基于上述信息提出了ACTOT模型,用于计算用户的主题分布,并通过用户-主题分布对PMF中用户的潜在因子特征向量进行正则化处理.
1.1 ACTOT模型表示
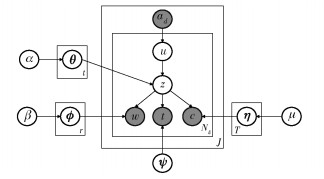
|
图 1 ACTOT图模型 |
|
|
表 1 ACTOT模型中各参数的含义 |
其中:θ、ϕ、η分别为服从参数为α、β、μ的狄利克雷先验分布的多项式分布,ψ为二项分布函数,图 1中深色节点ad、w、t、c为可观测已知量.
ACTOT模型的生成过程如下:
1)对论文集合J中的任意论文d,选取其用户集合ad中的任一用户u,计算该用户的用户-主题分布特征向量θ,再从参数为θ的多项分布函数中随机采样得到一个主题z;
2)计算主题z的主题-词特征向量ϕ,再从参数为ϕ的多项分布函数中随机采样得到一个词w;
3)计算主题z的主题-期刊/会议特征向量η,再从参数为η的多项分布函数中随机采样得到期刊/会议c;
4)计算主题z的主题-时间特征向量ψ,再从参数为ψ的Beta分布函数中随机采样得到一个时间戳,即论文发表时间t.
1.2 ACTOT模型的训练笔者利用Gibbs采样方法来计算ACTOT模型中的用户-主题分布θ,主题-词分布ϕ,主题-会议分布η,主题-时间分布ψ;初始值由参数α、β、μ、ψ1zdw、ψ2zdw决定,其中α、β、μ分别为决定θ、ϕ、η的超参数,ψ1zdw、ψ2zdw为Beta分布ψ的2个参数的初始值.
在Gibbs采样的每次迭代中,论文d中的词w被分配给操作过论文d的用户u和主题z.依式(1)依次计算论文集中任意论文的任意词出现的概率为
| $ \begin{array}{l} P\left({{z_{dw}}, {u_{dw}}\left| {{z_{ - dw}}, {u_{{ - _{dw}}}}, w, t, \alpha, \beta, \mu, \mathit{\boldsymbol{\eta }}\mathit{, }\mathit{\boldsymbol{\psi }}} \right.} \right)\propto \\ \frac{{N_{{u_{dw}}, {z_{dw}}}^{IT}+\alpha }}{{\sum\limits_{z' \in T} {N_{{u_{dw}}, {z_{dw}}}^{IT}+T\alpha } }} \cdot \frac{{N_{{z_{dw}}, {w_{dw}}}^{IV}+\beta }}{{\sum\limits_{w' \in V} {N_{{z_{dw}}{, _{w{'_v}}}}^{TV}+V\beta } }} \cdot \frac{{N_{{z_{dw}}{c_d}}^{TC}+\mu }}{{\sum\limits_{c' \in C} {N_{{z_{dwc'}}}^{TC}+C\mu } }} \end{array} $ | (1) |
其中
| $ \begin{array}{l} {\rm{Beta}}\left(\mathit{\boldsymbol{\psi }} \right)=\frac{{{{\left({1 - {t_{dw}}} \right)}^{\psi {{_z^1}_{dw}}}}t_{dw}^{\psi {{_z^2}_{dw}} - 1}}}{{B\left({\psi {{_z^1}_{dw}}, \psi {{_z^2}_{dw}}} \right)}}\\ B\left({\psi {{_z^1}_{dw}}, \psi {{_z^2}_{dw}}} \right)=\int_0^1 {{t^{\psi {{_z^1}_{dw}} - 1}}} {\left({1 - t} \right)^{\psi {{_z^1}_{dw}} - 1}}{\rm{d}}t \end{array} $ |
zdw、udw为论文d的词w指派给主题z和用户u;z-dw, u-dw为除本次指派外的其他指派;cd为将论文d指派给期刊/会议c;tdw为论文d中词w对应的时间戳,对同一篇论文d,其所有词的tdw均为论文d的发表时间.NITudw, zdw为除本次指派外用户u被指派给主题z的次数;NTVzdw, wdw为除本次指派外主题z被指派给词w的次数;NTCzdwcd为除本次指派外主题z被指派给期刊/会议c的次数.
每次迭代结束后,按式(2)更新所有主题的主题-时间分布ψ,然后基于更新的ψ进行下一次迭代.
| $ \begin{align} &\boldsymbol{\psi} \tilde{\ }\mathsf{B}\left(\psi {{_{z}^{1}}_{_{dw}}}, \psi {{_{z}^{2}}_{_{dw}}} \right), \psi {{_{z}^{1}}_{_{dw}}}={{{\bar{t}}}_{{{z}_{dw}}}}\left(\frac{{{{\bar{t}}}_{{{z}_{dw}}}}\left(1-{{{\bar{t}}}_{{{z}_{dw}}}} \right)}{s_{{{z}_{dw}}}^{2}}-1 \right)\\ &\ \ \ \ \ \ \ \ \ \psi {{_{z}^{2}}_{dw}}=\left(1-{{{\bar{t}}}_{{{z}_{dw}}}} \right)\left(\frac{{{{\bar{t}}}_{{{z}_{dw}}}}\left(1-{{{\bar{t}}}_{{{z}_{dw}}}} \right)}{s_{{{z}_{dw}}}^{2}}-1 \right)\\ \end{align} $ | (2) |
其中:tzdw、s2zdw为属于该主题的论文时间戳的样本均值和样本方差,计算公式为
| $ {{{\bar{t}}}_{{{z}_{dw}}}}=\frac{\sum\limits_{d=1}^{J}{\left(N_{d}^{\left({{z}_{dw}} \right)}{{t}_{{{z}_{dw}}}} \right)}}{\sum\limits_{d=1}^{J}{N_{d}^{\left({{z}_{dw}} \right)}}}, s_{{{z}_{dw}}}^{2}=\frac{\sum\limits_{d=1}^{J}{\left(N_{d}^{\left({{z}_{dw}} \right)}t_{d}^{2} \right)}}{\sum\limits_{d=1}^{J}{N_{d}^{\left({{z}_{dw}} \right)}}}-\bar{t}_{{{z}_{dw}}}^{2} $ |
在完成足够次迭代后,对于同一论文中的所有词,2次迭代得到的指派结果的区别小于给定阈值,此时已接近于实际指派情况,最后1次迭代后更新的ψ为最终的主题-时间分布.按式(3)~式(5)估算θ、ϕ、η,得到最终的用户-主题分布θ,主题-词分布ϕ,主题-会议分布η为
| $ \mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{=}\frac{N_{{{u}_{dw}}, {{z}_{dw}}}^{IT}+\alpha }{\sum\limits_{z'\in T}{N_{{{u}_{dw}}, z{{'}_{dw}}}^{IT}+T\alpha }} $ | (3) |
| $ \boldsymbol{\phi}=\frac{N_{{{z}_{dw}}, {{w}_{dw}}}^{IV}+\beta }{\sum\limits_{w'\in V}{N_{{{z}_{dw}}{{, }_{w{{'}_{v}}}}}^{TV}+V\beta }} $ | (4) |
| $ \mathit{\boldsymbol{ }}\!\!\eta\!\!\rm{=}\frac{N_{{{z}_{dw}}{{c}_{d}}}^{TC}+\mu }{\sum\limits_{c'\in C}{N_{{{z}_{dwc'}}}^{TC}+C\mu }} $ | (5) |
MFWT利用ACTOT计算用户的主题分布向量,并用该主题向量对PMF中的用户潜在因子特征向量作正则化处理,以提高PMF对评分较少用户的推荐效果,即解决PMF的用户数据稀疏性问题;同时借鉴CTR的思想,利用LDA计算论文的主题分布向量,并利用该主题向量对PMF中的项目潜在特征向量进行正则化处理,以解决PMF存在的项目冷启动问题.MFWT的图模型如图 2所示.
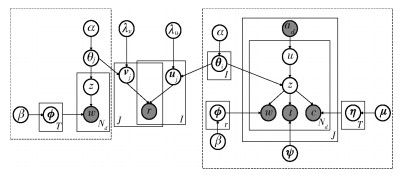
|
图 2 MFWT图模型 |
图 2中右侧虚线框内为笔者提出的ACTOT模型,r为用户对论文的已知评分,λu、λv分别为用户和论文潜在因子特征向量ui和vj的正则化参数,θi为用户的主题分布,θj为论文的主题分布.
MFWT的生成模型如下.
1)对于用户集合I中的每个用户i
①初始化用户的潜在因子特征向量xi,xi~N(0, λu-1IK),IK为单位矩阵,K为潜在因子特征向量的维度;
②利用ACTOT计算用户的主题特征向量θi,并将其作为用户潜在因子特征向量的正则化项,得到最终的用户潜在因子特征向量ui=xi+θi.
2)对于论文集合J中的每篇论文j
①初始化论文的潜在因子特征向量yj,yj~N(0, λv-1IK);
②利用LDA计算论文的主题特征向量θj,并将其作为论文的潜在因子特征向量的正则化项,得到最终的论文潜在因子特征向量vj=yj+θj.
3)对每个用户-论文对,计算用户i对论文j的评分rij,且rij~N(uiTvj, cij-1),有
| $ {{c}_{ij}}\left\{ \begin{align} &a, \ \ \ \text{if}\ \ {{\text{r}}_{ij}}=1 \\ &b, \ \ \ \text{if}\ \ {{\text{r}}_{ij}}=0 \\ \end{align} \right., a\gg b>0 $ |
其中cij为rij的置信参数,衡量了用户对论文评分值的可靠性,值越大,用户i对论文j的评分越可信.
为了在保证计算效果的基础上节省计算时间,笔者分别使用ACTOT和LDA单独求解θi和θj,然后将其作为PMF的已知量使用.
2.2 MFWT模型求解MFWT模型的求解是在给定θi、θj、rij的前提下,求解通过θi和θj进行正则化处理后的用户潜在因子特征向量ui和论文潜在因子特征向量vj,即求解ui和vj在已知评分数据rij情况下的最大后验概率p(U, V|R, σ2, σV2, σU2).其中,R为用户对论文的评分矩阵,U和V分别为进行矩阵分解后的用户潜在因子特征矩阵和论文潜在因子特征矩阵.σ、σU和σV分别为R、U和V对应的惩罚参数.
为方便求解,对后验概率估计取自然对数,求解其最大似然估计的值,即求解式(6)的最大值为
| $ \begin{align} &\begin{matrix} \ln p\left(\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}}\left| \mathit{\boldsymbol{R}}, {{\sigma }^{2}}, \sigma _{V}^{2}, \sigma _{U}^{2} \right.\right)=\\ -\frac{1}{2{{\sigma }^{2}}}\sum\limits_{i=1}^{I}{\sum\limits_{j=1}^{J}{{{I}_{ij}}{{\left[{{r}_{ij}}-{{\left({{\mathit{\boldsymbol{u}}}_{i}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{i}} \right)}^{\rm{T}}}\left({{\mathit{\boldsymbol{v}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)\right]}^{2}}}} \\ \end{matrix} \\ &\ \ \ \ \ \ \ -\frac{1}{2\sigma _{V}^{2}}{{\left({{\mathit{\boldsymbol{v}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)}^{\rm{T}}}\left({{\mathit{\boldsymbol{v}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)- \\ &\frac{1}{2}\left(\left(\sum\limits_{i=1}^{I}{\sum\limits_{j=1}^{J}{{{I}_{ij}}}} \right)\ln {{\sigma }^{2}}+IK\ln \sigma _{U}^{2}+JK\ln \sigma _{V}^{2} \right)+D \\ \end{align} $ | (6) |
其中:D为与模型无关的常数;Iij为指示函数,Iij=1为用户i对论文j评过分,Iij=0为用户i对论文j未评过分.
使用梯度上升法求解式(6)的最大值,去除式(6)的常数项后,等价于使用梯度下降法求解式(7)的最小值为
| $ \begin{matrix} E=\frac{{{\lambda }_{u}}}{2}\sum\limits_{i}{{{\left({{\mathit{\boldsymbol{u}}}_{i}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{i}} \right)}^{\rm{T}}}\left({{\mathit{\boldsymbol{v}}}_{i}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{i}} \right)+} \\ \frac{{{\lambda }_{v}}}{2}\sum\limits_{j}{{{\left({{\mathit{\boldsymbol{u}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)}^{\rm{T}}}\left({{\mathit{\boldsymbol{v}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)+} \\ \sum\limits_{i, j}{\frac{{{c}_{ij}}}{2}{{\left[{{r}_{ij}}-{{\left({{\mathit{\boldsymbol{u}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)}^{\rm{T}}}\left({{\mathit{\boldsymbol{v}}}_{j}}-{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right)\right]}^{2}}} \\ \end{matrix} $ | (7) |
其中:λu=σ2/σU2,λv=σ2/σV2.
使用迭代计算的方法求解用户i的潜在因子特征向量ui和论文j的潜在因子特征向量vj.对于用户-论文对{ui, vj}的更新为
| $ {{\mathit{\boldsymbol{u}}}_{i}}\leftarrow {{\left(\mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{C}}}_{i}}{{\mathit{\boldsymbol{V}}}^{\rm{T}}}+{{\lambda }_{u}}{{\mathit{\boldsymbol{I}}}_{K}} \right)}^{-1}}\left(\mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{C}}}_{i}}{{\mathit{\boldsymbol{R}}}_{i}}+{{\lambda }_{u}}{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{i}} \right) $ | (8) |
| $ {{\mathit{\boldsymbol{v}}}_{j}}\leftarrow {{\left(\mathit{\boldsymbol{U}}{{\mathit{\boldsymbol{C}}}_{j}}{{\mathit{\boldsymbol{U}}}^{\rm{T}}}+{{\lambda }_{v}}{{\mathit{\boldsymbol{I}}}_{K}} \right)}^{-1}}\left(\mathit{\boldsymbol{U}}{{\mathit{\boldsymbol{C}}}_{j}}{{\mathit{\boldsymbol{R}}}_{j}}+{{\lambda }_{v}}{{\mathit{\boldsymbol{ }}\!\!\theta\!\!\rm{ }}_{j}} \right) $ | (9) |
其中:U为用户潜在因子特征矩阵,且Uk×I=(ui)i=1I;Ci为用户i的置信参数矩阵,是对角元素为cij(j=1, …, J)的对角矩阵;Ri=(rij)j=1J为用户i的评分向量;V为论文潜在因子特征矩阵,且Vk×J=(vj)j=1J;Cj为论文j的置信参数矩阵,是对角元素为cij(i=1, …, I)的对角矩阵;Rj=(rij)i=1I为论文j的评分向量.
基于式(8)和式(9)计算得到的用户和论文潜在因子特征向量ui和vj,可预测用户对论文的评分为ȓij=uivj,然后对用户预测评分进行排序,选取评分值大的且没有被用户操作过的论文推荐给用户.
3 实验验证 3.1 实验方案笔者通过召回率和时间复杂度指标来评估MFWT模型的性能和效果.采用的数据集(http://www.citeulike.org/faq/data.adp,由CiteULike,http://www.citeulike.org提供)评估方案.数据集包含5 551个用户、16 980篇论文和204 986对用户-论文关系,其用户评分矩阵的稀疏性达99.8%,为高度稀疏矩阵.数据集中大部分用户收藏的论文数为20~30篇,97%的论文被用户收藏40次以内.笔者设计了如下实验:1)分析潜在特征空间维度K、参数λu和λv对MFWT模型性能的影响,以确定合理的特征空间维度、最佳的λu和λv取值;2)对比MFWT、CTR和PMF模型的推荐准确率和时间复杂度;3)通过评分数据较少用户的推荐准确率验证MFWT模型对数据稀疏性问题的解决效果.
3.2 实验结果及分析 3.2.1 参数K对MFWT模型性能的影响MFWT的潜在因子特征空间维度K与ACTOT和LDA的主题数一致.通过召回率和计算时间复杂度来衡量K对模型性能的影响.设置MFWT的置信参数cij中的a=1、b=0.01,λu=λv=100;ACTOT参数α=50/K,β=0.01,μ=0.1,ψzdi1=ψzdi2=1;LDA参数α=50/K、β=0.01.图 3(a)给出了推荐论文数量M=200时,召回率和时间复杂度随K的变化.
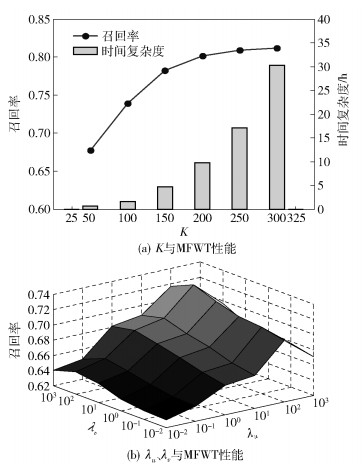
|
图 3 参数对MFWT模型性能的影响 |
如图 3(a)所示,当K值较小时,模型的召回率增长较快,时间复杂度也随着K的增大而升高;当K达到一定值时(K≥200),召回率的增加幅度逐渐减小,但时间复杂度却快速增加.因此综合考虑,在后续实验中,选取K=200.
3.2.2 参数λu,λv对MFWT模型性能的影响在式(8)和式(9)中,λu和λv越大,θi和θj所占比重越大.设置K=200,推荐论文数量M=200,除λu、λv外其他参数的设置同3.2.1小节.选取不同的λu和λv来衡量λu和λv对MFWT性能的影响.如图 3(b)所示,当λu、λv的值均接近100时,MFWT的召回率达到最优,因此在后续实验中,设置λu=100和λv=100.
3.2.3 MFWT、PMF和CTR模型的性能对比实验从召回率和时间复杂度2个指标对MFWT、PMF和CTR的性能进行对比.3种模型的论文推荐数量均为200,MFWT中λu=λv=100,CTR和PMF中λu=0.01,λv=100.
如图 4(a)所示,MFWT由于增加了ACTOT来计算用户的主题分布,其时间复杂度要比PMF和CTR高.但MFWT的时间复杂度主要由矩阵分解模型引入,且随K值的增大呈指数增长,相对来说,ACTOT只引入了较小的计算时间开销.从图 4(b)可以看出,不同K值下,MFWT的召回率明显优于PMF和CTR.可见,MFWT在增加较小的时间开销的情况下,推荐效果明显优于PMF和CTR.
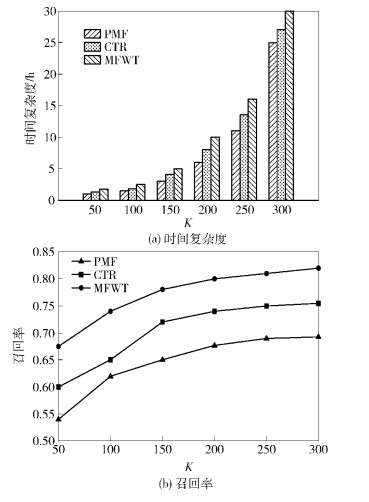
|
图 4 MFWT、PMF和CTR的性能对比 |
实验将用户按照其收藏论文的数量进行分类.如图 5所示,当用户收藏论文数少于20篇时,PMF和CTR主要是根据协同信息向用户推荐比较流行的论文,用户兴趣特征对算法的影响较小,因此模型的推荐效果不佳;而MFWT在协同信息的基础上同时考虑了用户和论文的主题信息,推荐效果较PMF和CTR有了提升.但随着用户收藏论文数量的增加,3种模型的推荐性能都呈下降趋势,这是因为收藏论文较多的用户会收藏一些较冷门的论文,此时协同信息所起的作用减弱,但MFWT因为考虑了用户和论文的主题特征,更准确地反映了用户的兴趣,模型的推荐效果仍然好于PMF和CTR.可见,MFWT即使在用户评分数据较少时也能取得较好的推荐效果,较好地解决了数据稀疏性问题.
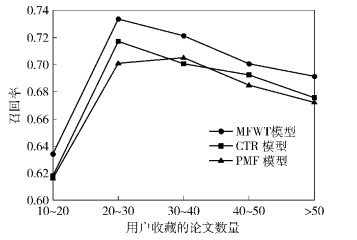
|
图 5 收藏不同论文数量用户的召回率对比 |
笔者针对学术论文推荐问题提出了一种混合模型推荐方法,基于用户的评分数据和论文的内容信息,将协同过滤方法中的PMF与基于内容推荐方法中的主题模型融合构造而成,同时解决了PMF对评分数据较少用户的数据稀疏性问题和新论文推荐时的冷启动问题.实验结果表明,相比PMF和CTR,MFWT在牺牲较小的时间复杂度的情况下,较好地提升了推荐结果的准确率.
但受限于矩阵分解模型的计算时间复杂度,MFWT的计算复杂度仍然较高,应用到大数据集上有一定局限.因此可考虑在更新用户特征向量和论文特征向量时,仅对重要特征空间进行更新.
| [1] | Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer , 2009, 42 (8) :30–37. doi:10.1109/MC.2009.263 |
| [2] | Mnih A, Salakhutdinov R. Probabilistic matrix factorization[C]//NIPS, 2007, 1(1):2-1. |
| [3] | 郭磊, 马军, 陈竹敏. 一种信任关系强度敏感的社会化推荐方法[J]. 计算机研究与发展 , 2013, 50 (9) :1805–1813. Guo Lei, Ma Jun, Chen Zhumin. Trust strength aware social recommendation method[J]. Journal of Computer Research and Development , 2013, 50 (9) :1805–1813. |
| [4] | 方耀宁, 郭云飞, 丁雪涛, 等. 一种基于标签迁移学习的改进正则化奇异值分解推荐算法[J]. 电子与信息学报 , 2013, 35 (12) :3046–3050. Fang Yaoning, Guo Yunfei, Ding Xuetao, et al. An improved regularized singular value decomposition recommender algorithm based on tag transfer learning[J]. Journal of Electronics and Information Technology , 2013, 35 (12) :3046–3050. |
| [5] | 郭磊, 马军, 陈竹敏, 等. 一种结合推荐对象间关联关系的社会化推荐算法[J]. 计算机学报 , 2014, 37 :219–228. Guo Lei, Ma Jun, Chen Zhumin, et al. Incorporating item relations for social recommendation[J]. Chinese Journal of Computers , 2014, 37 :219–228. |
| [6] | Jiang Cuiqing, Duan Rui, Jain H K, et al. Hybrid collaborative filtering for high-involvement products[J]. Decision Support Systems , 2015, 79 (C) :195–208. |


