2. 韩国釜山国立大学 电子工程系, 釜山
提出了一种基于时空特征和神经网络的视频超分辨率重建算法,实现了视频视觉分辨率质量和细节清晰度的提升.该算法综合考虑了外部图像块之间的关联映射关系和内部图像块间的相似性,利用深度卷积神经网络学习得到的拟合系数快速地重建视频细节.采用时空非局部特征相似性优化重建结果,将相邻视频帧间的非局部互补冗余信息融入学习视频帧结果中,解决了误匹配等问题,进一步提升了超分辨率性能.实验结果表明,所提方法在客观评价指标和主观视觉效果上均取得了较好的重建效果.
2. Department of Electronics Engineering, Korea Pusan National University, Busan, Korea
A video super-resolution algorithm based on spatial-temporal feature and neural network(STCNN) was proposed to improve the video visual resolution quality and details clarity. This algorithm comprehensively utilizes the correlation mapping relationship among external correlative blocks and the non-local similarity existed in the spatial-temporal neighboring internal blocks, thereafter, reconstructs the video details efficiently with the fitting parameters learned by deep convolutional neural network. Spatial-temporal feature similarities are introduced to optimize the reconstruction results, and to resolve the miss-match problem and improve the super-resolution performance by making full use of the complementary and redundant relationship between low-resolution video frames. Experiments demonstrate that the proposed algorithm outperforms existing algorithms in terms of both subjective visual effects and objective evaluation index.
视频拍摄过程中难免存在着各种各样的环境干扰,如运动或光学模糊、下采样、噪声、对焦失准等,往往无法得到精准的高分辨率图像或视频序列.通过超分辨率原始含噪低分辨率视频,将有助于提高后续视频利用过程的性能和效率.一般来说,视频超分辨率(VSR,video super resolution)算法依赖于内部非局部相似性信息[1-3]或外部图像块关联映射重建[4-6]实现.
笔者采用视频帧间的时空特征对基于深度卷积神经网络的快速学习重建算法进行优化,提出基于时空特征和神经网络的VSR重建算法,采用结构信息与Zernike矩特征结合的时空特征对待重建图像进行描述.不依赖于精确的亚像素运动估计,能适用于一些复杂的运动场景,且具有较好的旋转不变性和噪声鲁棒性.且在确保学习方法可有效地重建高频纹理细节信息优越性的同时,将帧间时空相关信息融入超分辨率处理后的视频中,进一步提升了VSR性能.
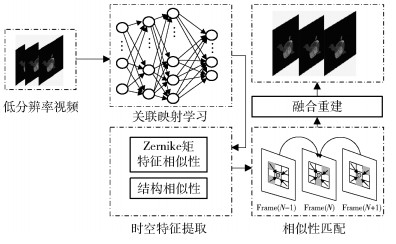
1 基于时空特征与神经网络的VSR算法 1.1 算法框架笔者提出的基于时空特征与神经网络的VSR算法的结构框图如图 1所示,包括基于深度卷积神经网络的高低分辨率图像块间关联映射重建和基于时空特征的相似性融合重建2个过程.其中基于卷积神经网络的关联映射重建部分利用外部图像块之间的关联映射关系来实现.由于重建部分所需的映射系数在关联学习过程中可以得到,所以可快速获得初始高分辨率估计结果.基于时空特征的相似性融合重建部分利用了时空特征对图像进一步描述,通过特征描述子和相邻图像间的相似性对初始高分辨率估计结果进行亚像素匹配和融合,修复上一步所得重建结果的时空不一致性,使视频帧可适应更加复杂的运动场景,提高了算法的抗噪能力.
|
图 1 基于时空特征与神经网络的超分辨率算法结构 |
由于视频相邻帧间存在着大量的互补冗余信息,这种时间上的相关信息以及待重建图像块邻近区域的空间相关信息有助于恢复超分辨率图像块中的缺失细节信息,提高基于深度卷积神经网络的单帧超分辨率重建算法的时空一致性.对于待重建视频块和其时空邻域的待融合的图像块,笔者提取图像块中的结构特征和Zernike矩特征等时空特征计算相似关系,对2个图像块之间的关联关系进行量化.
基于结构特征的结构相似性反映了2个图像块结构上的相似性,从亮度、对比度、结构3个方面度量图像的相似度[6],计算公式为
| $ \begin{array}{l} {\rm{SSIM}}\left({X, Y} \right)=l\left({X, Y} \right)c\left({X, Y} \right)s\left({X, Y} \right)=\\ \;\;\;\;\frac{{2{\mu _X}{\mu _Y}+{C_1}}}{{\mu _X^2+\mu _Y^2+{C_1}}}\frac{{2{\sigma _X}{\sigma _Y}+{C_2}}}{{\sigma _X^2+\sigma _Y^2+{C_2}}}\frac{{{\sigma _{X, Y}}+{c_3}}}{{{\sigma _X}{\sigma _Y}+{c_3}}} \end{array} $ | (1) |
其中:μX和μY分别为图像块X和图像块Y的均值,σX和σY则为标准差,σX, Y为X和Y图像块之间的协方差,C1、C2和C3为平衡常数,这里假设C2=2C3,式(1)可进一步化简为
| $ {\rm{SSIM}}\left({X, Y} \right)=\frac{{2{\mu _X}{\mu _Y}+{C_1}}}{{\mu _X^2+\mu _Y^2+{C_1}}}\frac{{2{\sigma _X}{\sigma _Y}+{C_2}}}{{\sigma _X^2+\sigma _Y^2+{C_2}}} $ | (2) |
结构相似性作为一个值域在[0,1]区间取值的区域块相似性评价参数,当其趋近于1时,表示2个图像块在结构上越相似.
Zernike矩特征是一种具有旋转、平移和尺度不变性的区域形状描述算子.对于以点(x, y)为圆心的单位圆内任意图像块I(x, y),其n阶m重Zernike矩特征定义为
| $ \begin{align} &{{Z}_{nm}}\left(I \right)=\frac{n+1}{\pi }\iint{_{{{x}^{2}}+{{y}^{2}}\le 1}I\left(x, y \right)V_{nm}^{*}\left(x, y \right)\text{d}x\text{d}y} \\ &\ \ \ \ \ \ \ \ \ \ \ \ \frac{n+1}{\pi }\sum\limits_{\rho \le 1}{\sum\limits_{0\le \theta \le 2\pi }{I\left(\rho, \theta \right)}}\ V_{nm}^{*}\left(\rho, \theta \right)\rho \\ \end{align} $ | (3) |
其中:
| $ \begin{array}{*{20}{c}} {{V_{nm}}\left({\rho, \theta } \right)=}\\ {\sum\limits_{s=0}^{n - \left| m \right|} {\frac{{{{\left({ - 1} \right)}^s}\left({2n+1 - s} \right)!{\rho ^{n - s}}}}{{s!\left({n+\left| m \right| - s} \right)!\left({n - \left| m \right| - s} \right)!}}{{\rm{e}}^{{\rm{jm}}\theta }}} } \end{array} $ | (4) |
Zernike矩特征相似性基于图像块间的Zernike矩特征进行相似性计算,其值越接近于1,表示2个图像块越相关.对于图像块X和图像块Y,其定义如式(5)所示,其中参数ε用来控制Zernike矩特征的衰减率.
| $ {\rm{ZFS}}\left({X, Y} \right)=\exp \left\{ { - \frac{{\left\| {{Z_{nm}}\left(X \right)- {Z_{nm}}\left(Y \right)} \right\|_2^2}}{{{\varepsilon ^2}}}} \right\} $ | (5) |
关联映射学习即学习高低分辨率图像块之间的关联关系,用来实现超分辨率图像块的目标.采用深度卷积神经网络学习这个关联关系,充分利用了深度卷积神经网络对于非线性关系的优越拟合性能.将学习得到的重建系数记作{W, B},其中W和B为以卷积层数为单位的参数对,利用这组参数对待超分辨率的视频帧进行多次卷积,从而快速得到基于外部先验约束的初始高分辨率估计结果.
在学习过程中,虽然具有较多网络层数、较小卷积核的神经网络有助于获得更好的学习效果[7],但是为了更好地权衡时间和效率的代价,笔者利用3层卷积神经网络学习高低分辨率图像块之间的关联映射关系.构建的深度网络利用卷积网络对传统重建过程(块提取与稀疏表示、非线性关联映射和重建)进行重新描述和拟合学习.笔者采用ImageNet图像库作为训练数据,采用与标准反向传播结合的随机梯度下降方法,通过多次迭代实现代价函数的最小化.代价函数设置为均方误差,如式(6)所示.
| $ \begin{array}{l} L\left({\mathit{\boldsymbol{W}}, \mathit{\boldsymbol{B}}} \right)={\rm{MSE}}\left({\mathit{\boldsymbol{W}}, \mathit{\boldsymbol{B}}} \right)=\\ \frac{1}{n}{\sum\limits_{i=1}^n {\left\| {F\left({{Y_i}, \mathit{\boldsymbol{W}}, \mathit{\boldsymbol{B}}} \right)- {X_i}} \right\|} ^2} \end{array} $ | (6) |
经过卷积神经网络学习,可得用于超分辨率视频帧的重建参数{W, B}.对这个参数对的具体利用过程,即整个重建过程,可用式(7)描述并实现.
| $ {F_i}\left(Y \right)=\max \left({0, W_i^*{F_{i - 1}}\left(Y \right)+{B_i}} \right) $ | (7) |
其中:{W, B}={W1, W2, W3, B1, B2, B3}作为重建系数,分别表示过滤器和偏差,i为重建过程卷积神经网络的层数.F0(Y)为输入图像,也可简单记为X.由于训练过程采用3层卷积神经网络,F3(Y)即最后输出的高分辨率图像.
通过对待超分辨率重建图像的3层卷积处理,可快速且有效地实现高分辨率视频帧的初始估计.在此基础上,笔者采用时空非局部相似性来优化重建结果,实现外部先验约束和内部相似性约束的综合利用.
1.4 基于时空特征的相似性匹配与融合假设待处理的图像块为ys,其待搜索区域,即其空间上的邻域图像块以及时间域上的相似图像块,记为{yp}p∈N.通过时空特征提取,可得到2个图像块结构相似关系的量化度量,通过阈值过滤实现亚像素匹配.对于小于阈值的图像块,认为是无关图像块进行去除,避免无关图像块对待处理图像融合结果的影响,且进一步提升算法效率.
为了更精确描述匹配得到的待融合相似图形块集的关联关系,平衡提取得到的时空特征,采用几何平均计算待融合图像块的融合权重,如式(8)所示.
| $ \omega \left({{y_p}} \right)=\sqrt {{\rm{ZFS}}\left({{y_s}, {y_p}} \right){\rm{SSIM}}\left({{y_s}, {y_p}} \right)} $ | (8) |
基于所得的融合权重,对待重建图像块周围所有待融合的图像块,通过式(9)作为融合函数进行重建.为了进一步描述待融合图像块所属的图像帧,引入变量T进行描述,ω(ypT)和ypT分别表示第T帧以(i, j)为中心的图像块的融合权重和区域信息.
| $ {y_s}'=\frac{{\sum\limits_{T \in \left[{{T_1}{T_2}} \right]} {\sum\limits_{p \in N\left(s \right)} {\omega \left({y_p^T} \right)y_p^T} } }}{{\sum\limits_{T \in \left[{{T_1}{T_2}} \right]} {\sum\limits_{p \in N\left(s \right)} {\omega \left({y_p^T} \right)} } }} $ | (9) |
基于时空特征和神经网络的VSR算法的实现分为2个过程:一个是基于深度卷积神经网络的关联映射参数学习过程,另一个是基于时空特征和学习得到重建参数的VSR重建过程.算法实现步骤如下.
算法:基于时空特征和神经网络的VSR重建
输入:低分辨率视频序列
输出:高分辨率视频序列
步骤1 对待重建的低分辨率视频序列
步骤2 对第t(t=1, 2, …, T)帧图像,从中提取出待优化的图像块集
步骤3 对第s块待优化图像块ys,遍历得到其周围搜索区域内的待搜索图像块{yp}p∈N(s)
步骤4 计算ys与yp之间的结构相似性,按照预设的阈值,过滤无关图像块,得到待融合的图像块集{y′p}p∈N(s)
步骤5 按照式(8),计算ys和y′p之间的融合权值
步骤6 按照式(9),更新待重建区域块ys,得到y′s
步骤7 若s < max block,则重复步骤3,反之,得到对第t帧图像的最终高分辨率估计Yt
步骤8 若t < T,则重复步骤2,反之,得到视频序列
实验采用的视频序列来自http://trace.eas.asu.edu/yuv/index.html的标准视频序列和来自http://www.youku.com的空间视频序列.通过对原始视频序列进行3倍下采样,添加均值为0,方差为2的高斯噪声,得到低分辨率视频序列.分别采用对比算法NL-SR[1]、ScSR[4]、ZM-SR[2]、SRCNN[6]、DPSR[8]和笔者提出的基于时空特征和神经网络的VSR(STCNN,spatial-temporal feature and neural network)算法对低分辨率视频进行3倍超分辨率处理.下面从客观指标和主观视觉效果对各个算法所得的高分辨率视频进行对比和评价.
2.1 客观评价指标采用峰值信噪比(PSNR,peak signal to noise ratio)、结构相似性(SSIM,structural similarity index)、特征相似性(FSIM,feature similarity index)和均方根误差(RMSE,root mean squared error)4个评价指标,对超分辨率性能进行定量客观评价PSNR值越高,RMSE的值越低,表明超分辨率后视频帧与原始视频帧越接近.对于FSIM和SSIM,所得的评估值越接近于1,重建后视频帧就可获得与原始视频帧更高的特征和结构相似性,即得到更好的重建效果.
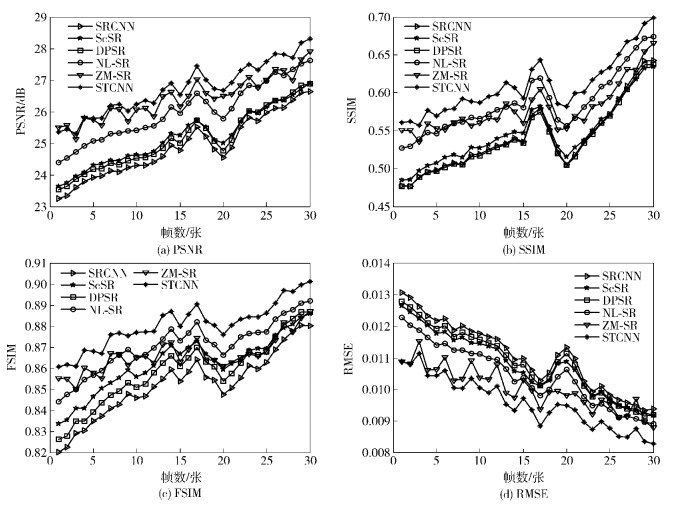
基于以上4个客观评价指标,对标准视频序列Suzie、CoastGuard和Football以及空间视频序列Satellite1和Satellite2分别采用NL-SR、ZM-SR、DPSR、SRCNN、ScSR和笔者提出的STCNN算法进行超分辨率处理,并对每一个视频序列给出对比指标曲线图,其中Football序列的客观指标评价曲线图如图 2所示.通过对曲线图的观察,可明显地发现对于每一帧图像,笔者所提的方法均获得了更好的超分辨率效果,即取得了更高的PSNR、FSIM和SSIM值,以及更低的RMSE值.
|
图 2 Football视频序列的客观指标评价 |
为了进一步描述笔者所提算法在这5个序列上的指标评估结果,对每个序列在各算法处理后的结果的评估指标计算了1个平均值,如表 1所示.通过对平均评价指标进行分析可看出,与基于学习的单帧重建算法ScSR、SRCNN和DPSR对比,笔者提出的STCNN算法在各个指标上均获得了一定的提升,这主要是因为STCNN算法采用时空非局部相似性进行了进一步的优化,从而更好地保持了视频序列的时空一致性.与基于相似块匹配的重建算法NL-SR和ZM-SR相比较,STCNN算法获得了更好的重建效果,这是因为STCNN算法充分利用了外部图像块先验约束信息进行初始估计,从而获得了更多的低质视频中缺失的细节信息.
|
|
表 1 不同算法对5组视频序列重建效果的平均客观评价指标 |
下面从视觉效果上进一步验证STCNN算法的性能.图 3是空间运动视频Satellite1的1帧,如图 3所示,框中所圈的放大区域包括飞行器的上翼以及黑色的背景.通过对比可以发现,DPSR、ScSR和SRCNN算法都在黑色的背景区域产生了一些灰色的噪点,其中DPSR算法最为明显.这是由于其抗噪性能差,对于低分辨率视频帧中存在的噪声信息进行了错误的超分辨率处理.而NL-SR、ZM-SR和笔者提出的STCNN算法的抗噪效果要好很多.NL-SR算法在边缘部分产生了马赛克现象,ZM-SR算法则较为模糊,笔者提出的STCNN算法获得了更加平滑的边缘和清晰的视频效果.

|
图 3 Satellite1视频序列的超分辨率重建视觉效果 |
综合利用低分辨率和高分辨率图像块之间的关联映射关系,以及低分辨率相邻视频帧间的非局部互补冗余信息进行VSR重建.提出了一种基于时空特征和神经网络的VSR算法STCNN,进一步提升了视频的视觉分辨率质量和细节清晰度.该算法利用深度卷积神经网络处理非线性关联关系时强大的拟合能力,学习高低分辨率图像块之间的关联映射,实现了快速超分辨率视频帧的目的.为了进一步利用帧间时空关系来优化重建结果,笔者采用时空特征相似性和结构相似性来描述视频帧间的互补冗余关系,通过特征描述子以及结构信息相关性对初始高分辨率估计结果进行相似性匹配和融合,不依赖于精确的亚像素运动估计,能适用于一些复杂的运动场景,且具有较好的旋转不变性和噪声鲁棒性.实验结果表明,笔者所提方法在客观评价指标和主观视觉效果上均取得了较好的重建效果.
| [1] | Protter M, Elad M, Takeda H, et al. Generalizing the nonlocal-means to super-resolution reconstruction[J]. IEEE Transactions on Image Processing , 2009, 18 (1) :36–51. doi:10.1109/TIP.2008.2008067 |
| [2] | Gao X, Wang Q, Li X, et al. Zernike-moment-based image super resolution[J]. IEEE Transactions on Image Processing , 2011, 20 (10) :2738–2747. doi:10.1109/TIP.2011.2134859 |
| [3] | Timofte R, De S V, Van G L. A+:adjusted anchored neighborhood regression for fast super-resolution[C]//Asian Conference on Computer Vision. Singapore:Springer, 2014:111-126. |
| [4] | Yang Jianchao, Wright J, Huang Thomas, et al. Image super-resolution as sparse representation of raw image patches[C]//Conference on Computer Vision and Pattern Recognition(CVPR), Anchorage:IEEE, 2008:1-8. |
| [5] | Hu Yanting, Wang Nannan, Tao Dacheng, et al. SERF:a simple, effective, robust, and fast image super-resolver from cascaded linear regression[J]. IEEE Transactions on Image Processing , 2016, 25 (9) :4091–4102. doi:10.1109/TIP.2016.2580942 |
| [6] | Dong Chao, Loy C C, He Kaiming, et al. Learning a deep convolutional network for image super-resolution[M]//European Conference on Computer Vision 2014(ECCV). Zurich:Springer International Publishing, 2014:184-199. |
| [7] | Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]//Advances in Neural Information Processing Systems(NIPS). Nevada:NIPS, 2012:1097-1105. |
| [8] | Zhu Yu, Zhang Yanning, Yuille A L. Single image super-resolution using deformable patches[C]//Conference on Computer Vision and Pattern Recognition(CVPR). Columbus:IEEE, 2014:2917-2924. |


