2. 东南大学 电气工程学院, 南京 210096
研究了一种用于车载传感器自供电的压电和电磁复合式能量收集技术,给出了系统的数学模型,分析了系统共振频率与系统结构参数的关系,设计了一套压电和电磁复合式能量收集装置.实验结果表明,数学模型基本反映了系统的输出特性,在共振频率为18 Hz,加速度为0.5 g时,复合式能量收集装置的最大负载功率为3.75 mW,相比于采用单一电磁技术时的最大负载功率3.2 mW增加了17%.
2. Electrical Engineering Scholl, Southeast University, Nanjing 210096, China
The piezoelectric and electromagnetic energy harvesting technology for vehicle sensors self-powered was studied. The mathematical models for the composite energy collection system was put forword, and the relationship about the resonance frequency of the system was analyzed with regard to the system configuration parameters. A piezoelectric and electromagnetic energy harvesting device was designed. Experiment shows it has good agreement with the analytical results in trend. The maximum of load power of the composite harvester achieves 3.75 mW at the resonant frequency of 18 Hz with acceleration of 0.5 g, and is increased by 17% compared with 3.2 mW of the single electromagnetic technique.
随着电动汽车智能化的发展,车用微型传感器节点的供能问题成为亟待解决的难题之一[1-2]. 传统的由电池或电力线布线供电方式存在污染环境和难以维护的缺陷. 因此,收集汽车自身振动能量供电可以不依赖电池或线束对设备进行单独供电[3-4].
电磁和压电复合式能量收集系统(EPCECS,electromagnetic and piezoelectric composite energy collection system)可用来解决低供能问题[5-6]. 笔者设计了一种结合压电技术和电磁技术的复合式能量收集装置,在共振情况下的发电性能测试结果表明,在共振频率为18 Hz,加速度为0.5 g时,复合式能量收集装置的最大负载功率为3.75 mW,相比于采用单一的电磁技术时的最大负载功率3.2 mW增加了17%.
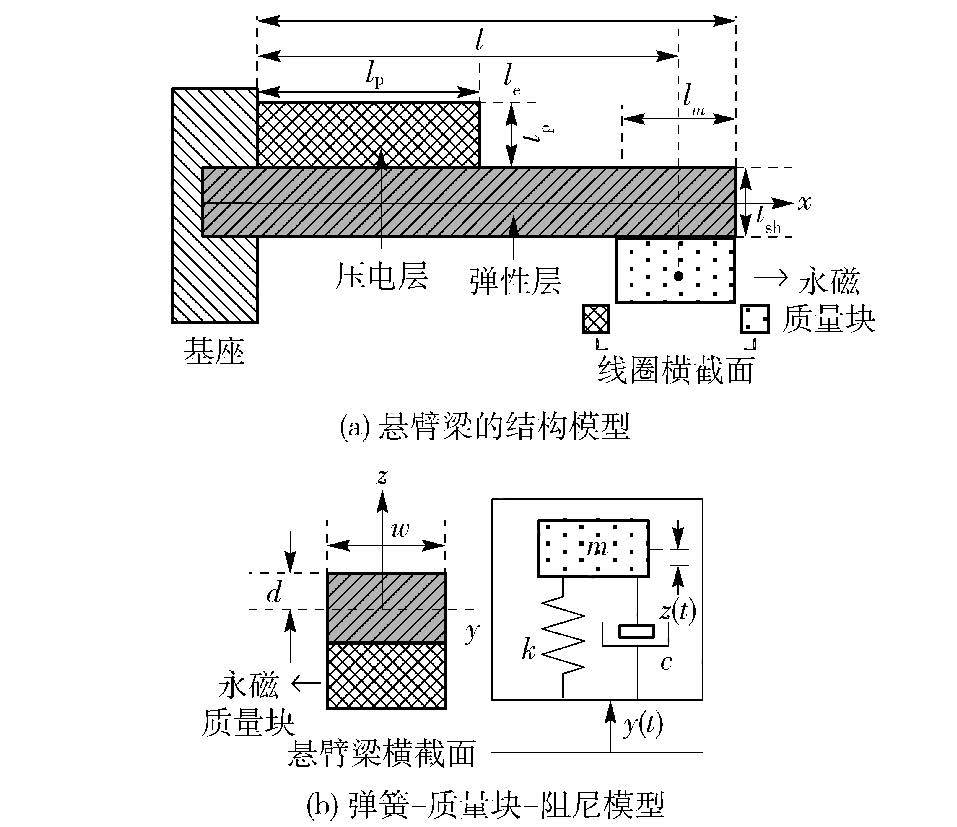
1 EPCECS数学模型 1.1 EPCECS振动模型复合能量收集装置如图 1(a)所示,压电悬臂梁产生受迫振动,用弹簧—质量块—阻尼单自由度系统模型来描述悬臂梁在外部振动激励下引起的振动模型[1-2],如图 1(b)所示. 振动系统的模型为
| $\ddot z\left( t \right) + 2\xi {\omega _n}\dot z\left( t \right) + \omega _n^2z\left( t \right) = - \ddot y\left( t \right)$ | (1) |
|
图 1 悬臂梁的结构模型和振动阻尼模型 |
其中:y(t)为外部环境基础的振动位移,y(t)=Ysinωt,z(t)为质量块的相对振动位移,ξ为阻尼比率,
利用Matlab求得稳态解为
| $z\left( t \right) = {{\sin \left( {\omega t - \varphi } \right)y{{\left( {{\omega \over {{\omega _n}}}} \right)}^2}} \over {\sqrt {{{\left( {1 - {{\left( {{\omega \over {{\omega _n}}}} \right)}^2}} \right)}^2} + {{\left( {2\xi \left( {{\omega \over {{\omega _n}}}} \right)} \right)}^2}} }}$ | (2) |
根据横截面转换法和惯性矩平行轴定理,悬臂梁在x=0~lp段和x=lp~le段的等效截面惯性矩为
| $\eqalign{ & {I_1} = \eta \left[ {{{\omega t_{sh}^3} \over {12}} + \omega {t_{sh}}{{\left( {{{{t_{sh}}} \over 2} - d} \right)}^2}} \right] + \cr & \left[ {{{\omega t_p^3} \over {12}} + \omega {t_p}{{\left( {{{{t_p}} \over 2} - d} \right)}^2}} \right] \cr & {I_2} = {{\eta \omega t_{sh}^3} \over {12}} \cr} $ | (3) |
其中:d为压电层下表面距中性轴的距离,d=(ηt2sh-t2p)/2(tp+ηtsh),tp和tsh分别为压电层和弹性层的厚度,w为悬臂梁的宽度,η=Ysh/Yp,Ysh、Yp分别为弹性层和压电层的弹性模量,由结构力学相关理论可知,该悬臂梁的系统有效弹性系数为
| $K = {{3{Y_p}{I_1}{I_2}} \over {({l^3}_e - {{({l_e} - {l_p})}^3}){I_2} + {{({l_e} - {l_p})}^3}{I_1}}}$ |
利用系统基频振动角频率公式得
| $\eqalign{ & {\omega _n} = \sqrt {{K \over m}} = \cr & \sqrt {{{3{Y_p}{I_1}{I_2}} \over {[(l_e^3 - {{({l_e} - {l_p})}^3}){I_2} + {{({l_e} - {l_p})}^3}{I_1}](\Delta m + 0.236M)}}} \cr} $ | (4) |
由压电方程[2]可知,当悬臂梁在受到z方向惯性力作用下,形成耦合电场. 对于压电应变δ=-d31E3,可将其等效为一个在悬臂梁末端的集中力FE,在式(1)中加入电场力后得
| $m\ddot z\left( t \right) + c\dot z\left( t \right) + kz\left( t \right) = - m\ddot y\left( t \right) - {F_E}\left( t \right)$ | (5) |
集中力作用下悬臂梁弯矩为Mx=F(le-x),根据应变和弯矩的关系,压电应变为
| $ - {d_{31}}{E_3} = {F_E}({l_e} - x)z/{Y_p}{I_1}$ | (6) |
压电片等效电容为CP=Sε33/tp,其中ε33为压电材料的介电常数,S为压电层的面积. 因为电极表面等电势,所以电极间电场E3可视为均匀电场,E3=-U/tp,U为极间电压. 计算压电层的平均应变为
| ${{{d_{31}}U} \over {{t_p}}} = {1 \over {{l_p}{t_p}}}\int\!\!\!\int {{{{F_E}{{({l_e} - x)}^z}} \over {{Y_p}{I_1}}}} dxdz$ | (7) |
解得FE,代入式(5)得
| $\left. \matrix{ z = {{{\omega ^2}y - {k_1}U/m} \over { - {\omega ^2} + j2\xi \omega {\omega _n} + \omega _n^2}} \hfill \cr {k_1} = 4{{{d_{31}}{Y_p}{I_1}} \over {(2{l_b} - {l_p})({t_p} + 2d){t_p}}} \hfill \cr} \right\}$ | (8) |
根据热平衡原理,利用无穷小的单元体内产生的系统内能可得压电层的电场能为
| ${W_E} = 2\left( { - {k_2}FU + {1 \over 2}{{{\varepsilon _{33}}w{l_p}} \over {{t_p}}}{U^2}} \right)$ | (9) |
其中k2=d31wlp(2lb-lp)(tp+2d)/4I1.
式(9)对电压U求微分,得压电层上的电荷量,再对时间微分,可得电流表达式为
| $i = - {{dq} \over {dt}} = {k_2}{{dF} \over {dt}} - {C_P}{{dU} \over {dt}}$ | (10) |
记F=|F|ejωt,U=|U|ejωt,代入式(10),整理后得
| ${{F{k_2}} \over {{C_P}}} = U + {i \over {j\omega {C_P}}}$ | (11) |
考虑到F=Kz,再将式(8)代入式(11),当i=0时,整理得压电振动发电机在环境激振作用下的开路电压和振动激励加速度之间的关系为
| ${V_o} = \left( {{{{{K{k_2}} \over {{C_P}}}{A_{in}}} \over { - {\omega ^2} + j2\xi \omega {\omega _n} + {\omega ^2}_n(1 + {k_p})}}} \right)$ | (12) |
其中
当外接负载为R时,假设压电层的容抗为Xc,其输出平均功率[6]为
| ${P_p} = {1 \over T}\int_0^T {{{RV_o^2} \over {{{\left( {{X_c} + R} \right)}^2}}}dt = {1 \over 2}{{RV_o^2} \over {{{\left( {{X_c} + R} \right)}^2}}}} $ | (13) |
由振动模型公式(1)推导得
| $\eqalign{ & z\left( t \right) = Zsin\left( {\omega t - \varphi } \right) = \cr & {{Y{\omega ^2}sin\left( {\omega t - \varphi } \right)} \over {{{\left\{ {{{(\omega _n^2 - {\omega ^2})}^2} + {{c\omega } \over {{m^2}}}} \right\}}^{1/2}}}} \cr} $ | (14) |
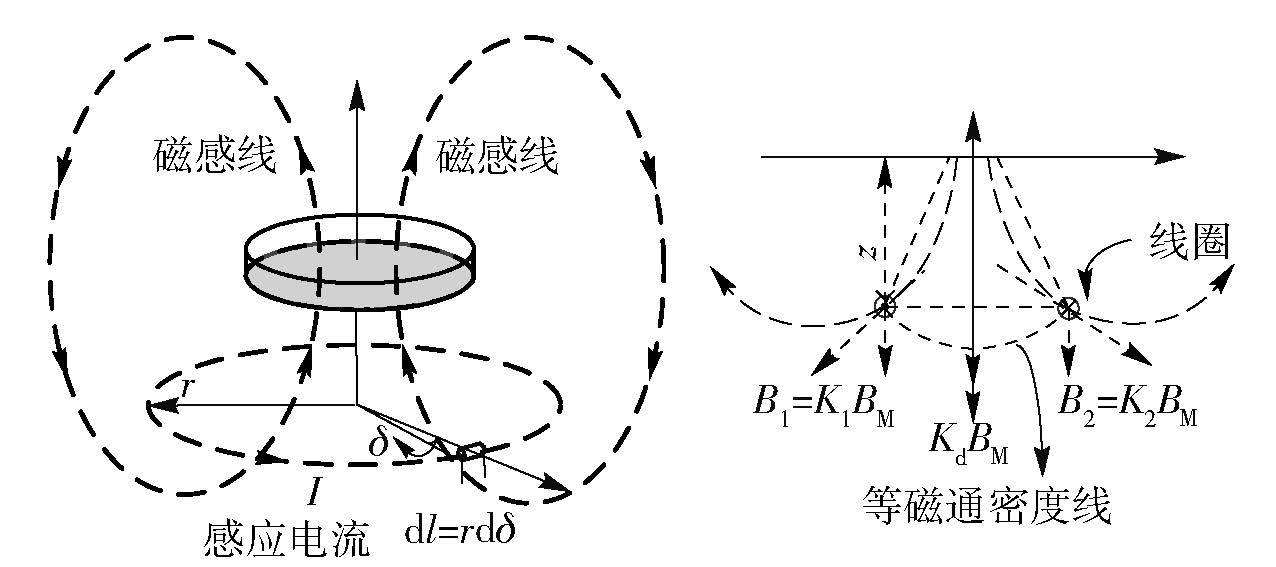
当变化的磁场穿过一个闭环的线圈区域S,它产生的感应电动势为
| $\varepsilon = - {{d\varphi } \over {dt}} = - \int\limits_S {\left( {{{dB} \over {dt}}} \right)dS} - \oint_C {\left( {B\dot z} \right)} dl$ | (15) |
磁铁周围的磁通密度B随空间位置变化而变化,如图 2所示,设K为与磁铁和线圈相对位置相关的系数,K小于等于1,且随着磁铁和线圈距离的增大而减小. 在正弦激励的作用下,永磁铁与线圈以正弦规则相对运动,磁通密度B1、B2为
| $\eqalign{ & {B_1} = {K_1}B\left( \omega \right) = {K_1}[{B_M}cos\left( {\omega t - \varphi } \right)z + {B_M}cos\left( {\omega t - \varphi } \right)x] \cr & {B_2} = {K_2}B\left( \omega \right) = {K_2}[{B_M}cos\left( {\omega t - \varphi } \right)z + {B_M}cos\left( {\omega t - \varphi } \right)x] \cr} $ | (16) |
其中:BM为永磁铁磁通密度的最大值,K1、K2为在不同空间位置磁场垂直分量的磁密度系数,即磁力值与最大磁力值的比率. 如果线圈的空间位置与永磁铁磁场的中间轴是对称的,K1等于K2. 替换式(16)到式(15),得电动势为
| $\eqalign{ & \varepsilon = N - \int_0^{2\pi } {(dB/dt){1 \over 2}{r^2}d\delta } - \cr & \int_0^{2\pi } {\left( {B\dot z} \right)rd\delta } + \int_\pi ^{2\pi } {\left( {B\dot z} \right)rd\delta } = \cr & \pi {r^2}NK{B_M}\omega sin\left( {\omega t - \varphi } \right) \cr} $ | (17) |
其中:r为线圈半径,δ为圆周角,已知线圈内阻Rs和输出电阻Ro的情况下,输出平均功率为
| ${P_e} = {1 \over T}\int_0^T {{{{R_o}{\varepsilon ^2}} \over {{R_s} + {R_o}}}} dt = {1 \over 2}{{{R_o}{{(\pi {r^2}NK{B_M}\omega )}^2}} \over {{R_s} + {R_o}}}$ | (18) |
|
图 2 磁感应曲线分布 |
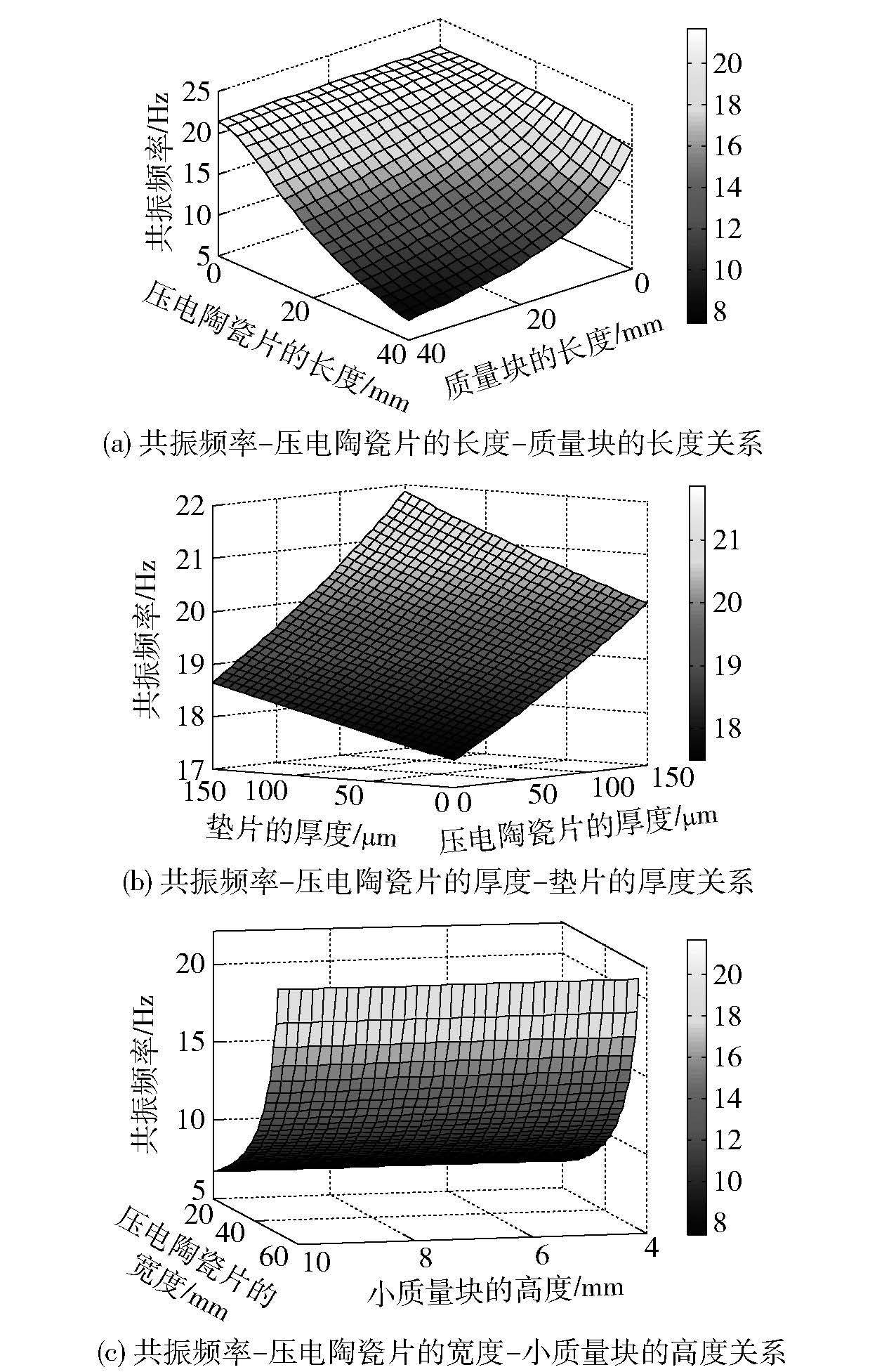
利用Matlab软件对EPCECS模型进行了数值仿真,压电悬臂梁共振频率与悬臂梁的长度、悬臂梁的宽度、质量块的长度、质量块的高度和压电陶瓷片的结构参数的关系如图 3所示.
|
图 3 共振频率与悬臂梁结构参数的关系 |
从图 3(a)可以看出,在悬臂梁质量块的长度确定的情况下,共振频率随着压电陶瓷片的长度的增加而降低,在压电陶瓷片的长度一定的情况下,共振频率随着质量块的长度的增加而减小. 从图 3(b)可以看出,压电悬臂梁的共振频率随着压电陶瓷片的厚度和金属垫片的厚度的增加而增加. 从图 3(c)可以看出,在小质量块的高度不变的情况下,压电悬臂梁的共振频率随着悬臂梁的宽度的增加而升高,而当悬臂梁的宽度确定后,压电悬臂梁的共振频率随着小质量块的高度的变化并不发生改变.
通过仿真分析,可以获得输出电压与质量块质量和输入频率的关系,在一定的振动频率上,系统输出电压随着质量块质量的增加而增加,系统在共振频率处的输出电压明显高于其他频率的输出电压.
3 EPCECS性能测试与分析 3.1 EPCECS设计与实验由仿真分析可以看出,收集装置的共振频率与悬梁臂的结构参数相关联. 由实验测定电动汽车的速度为40 km/h,相对应的频率大概为18 Hz,故系统共振频率设计为18 Hz,结合仿真分析,最终确定了压电悬臂梁结构的尺寸参数,如表 1所示.
|
|
表 1 复合式能量收集装置的参数 |
实验中使用的设备主要包括信号发生器、功率放大器、激振器、示波器和数字万用表. 实验中振动频率为18 Hz,振动加速度为0.5 g.
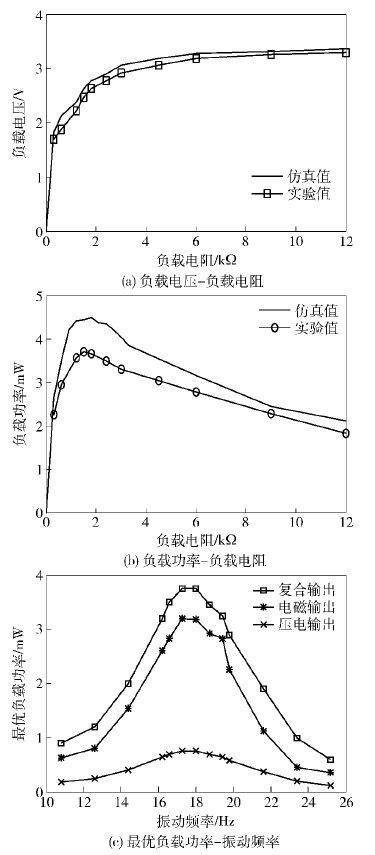
3.2 EPCECS实验结果分析复合式能量收集装置的最优负载电阻是由内部等效电路和转换电路的参数决定的,利用PSPICE电路仿真和实验方法确定最优负载电阻值大约为1.5 kΩ. 在共振频率下,负载电压、负载功率的仿真结果和测量值如图 4(a)和4(b)所示. 从图中可以看出,负载功率首先呈上升趋势,并在最佳负载电阻时达到峰值,当负载电阻大于1.5 kΩ时负载功率随之下降,而负载电压则始终随着负载电阻上升. 测量值与数值仿真结果十分接近. 在最优负载电阻时,运用数值仿真计算负载电压和负载功率分别为2.6 V和4.48 mW,测量值则为2.4 V和3.75 mW.
|
图 4 仿真与实验结果对比曲线 |
图 4(c)显示了最优负载电阻时复合式和单一型能量收集技术的最优负载功率,复合式能量收集技术获得的最大负载功率为3.75 mW,与单一型电磁技术实验在共振频率处得到的3.2 mW负载功率相比,增加了17%. 单一压电工作模式下的最优负载功率较低,其稳定后的值为0.75 mW.
4 结束语EPCECS整合了压电和电磁能量收集技术,可以有效地提高能量收集密度. 笔者分析给出了系统的数学模型,并进行了仿真分析,通过实验证明了复合式能量收集的效果. 在共振频率为18 Hz,加速度为0.5 g时,复合式能量收集装置的最大负载功率为3.75 mW,相比于采用单一的电磁技术时的最大负载功率3.2 mW增加了17%.
| [1] |
Williams C B, Yates R B. Analysis of a micro electric generator for micro systems[J]. Sensors and Actuators:Physical , 1996, 52 (1-3) :8–11.
doi:10.1016/0924-4247(96)80118-X ( 0) 0)
|
| [2] |
Xia Changliang, Song Zhanfeng. Wind energy in China:current scenario and future perspectives[J]. Renewable and Sustainable Energy Reviews , 2009, 13 (8) :1966–1974.
doi:10.1016/j.rser.2009.01.004 ( 0) 0)
|
| [3] |
Yu Hua, Zhou Jielin, Deng Licheng, et al. A vibration-based MEMS piezoelectric energy harvester and power conditioning circuit[J]. Sensors , 2014, 14 (2) :3323–3341.
doi:10.3390/s140203323 ( 0) 0)
|
| [4] |
Yang B, Lee C, Kee W L, et al. Hybrid energy harvester based on piezoelectric and electromagnetic mechanisms[J]. J Micro-Nanolithogr MEMS MOEMS , 2010, 9 (2) :023002.
doi:10.1117/1.3373516 ( 0) 0)
|
| [5] |
Salim M, Aljibori H S S, Salim D. A review of vibration-based MEMS hybrid energy harvesters[J]. Journal of Mechanical Science and Technology , 2015, 29 (11) :5021–5034.
doi:10.1007/s12206-015-1050-9 ( 0) 0)
|
| [6] |
刘承玺. 压电-电磁复合发电技术及其实验研究[D]. 哈尔滨:哈尔滨工业大学, 2012.
http://cdmd.cnki.com.cn/article/cdmd-10213-1013036428.htm ( 0) 0)
|


