针对多条传输线间的串扰问题,在对耦合传输线信道传输矩阵进行特征值分解的基础上,提出了3条微带传输线间的串扰抵消方法,研究了该方法的电路实现结构,并给出了电路的相关参数.仿真结果显示,该方法能明显改善信号眼图的质量,串扰抵消效果良好.
Crosstalk is one of the bottlenecks in high-speed circuits for rate and density continuing increasing. Aiming at the problem of crosstalk between multiple transmission lines, a crosstalk cancellation method of three coupled microstrip lines based on eigen value decomposition of coupled transmission lines-channel transmission matrix was proposed. The circuit implementation structure of the method was studied and the circuit parameters were provided. Simulations show that crosstalk can be mostly eliminated and the quality of eye diagram can be improved obviously.
随着集成电路技术的进步和客户需求的提高,电子产品向着处理速度更高、物理尺寸更小的方向发展,这使得集成电路的工作频率越来越高、规模越来越大、引脚越来越多,印制电路板上电路的密度越来越大,芯片引脚间的信号互连就面临着巨大的挑战. 这一挑战主要是互连线上日益突出的信号完整性问题[1]. 串扰是4类信号完整性问题之一,它已经成为电路系统继续提高速率的瓶颈,是制约高速电路发展的重要原因之一[2-3].
信号线间的电磁耦合形成了串扰,当多条传输线进行信号传输时,线路中传输的信号会泄漏到其他临近线路中. 在高速互连电路中,串扰会导致2种后果:一是串扰会在相邻的传输线上产生噪声,这将降低系统的噪声容限;二是相邻传输线上信号的不同阶跃方向会导致不同的时延,这将恶化系统的时序[4]. 特别是当多条干扰线同时耦合到一条受扰线时,就会导致每一条干扰线都在受扰线上施加额外的噪声,它能使多条传输线出现阻抗和延迟过于依赖数据模式的现象,从而影响多条高速互连线的性能.
为了减小多条传输线间的串扰,目前国内外研究者主要是从电路板和传输线的物理结构角度来考虑抑制串扰[5-10],这类方法效果有限且随着电路密度的增大应用范围越来越窄. 实际上,如果避开从电磁耦合这一角度来考虑串扰问题,那么抑制串扰的根本目的就是在信号线的输出端尽可能地恢复输入信号. 从通信的角度来看,传输线的输入端和输出端分别对应于通信系统的发送端和接收端,串扰就是噪声,为了从叠加了串扰的接收波形中提取信号的过程就是检测,因此,通信中的各种信号检测技术就可以用于抑制串扰[4]. 文献[11-12]基于多输入多输出技术(MIMO,multi-input and multi-output),利用类似于无线通信系统中的空分复用技术在传输线的输出端进行串扰抵消,并给出了应用于2条传输线上的方案和仿真结果. 文献[13]在MIMO的基础上提出了耦合传输线信道传输矩阵(CTL-CTM,coupled transmission lines-channel transmission matrix)的概念,并在对其进行矩阵分解的基础上提出了一种基于酉变换的串扰抵消方法,并给出了该方法应用于2条传输线上的仿真结果. 由于在实际应用中,更普遍的要求是消除多条传输线间的串扰,因此需要研究多条传输线间的串扰抵消方案,笔者在对多条耦合传输线信道传输矩阵进行特征值分解(EVD,eigen value decomposition)的基础上研究了更具有一般性的3条微带传输线间串扰抵消方法,并给出了该方法的电路结构和参数,仿真结果显示该方法串扰抵消效果良好.
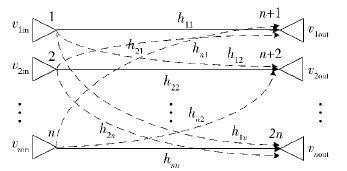
1 CTL-CTM分析参照MIMO系统,一般情况下,对于一组n条耦合微带传输线来说,由于传输线以及传输线间的信号耦合都可以看作是信道,因此,其中的任意一个输出端和其他所有输入端之间都存在信道关系,那么,输出信号与输入信号就可以表示成如图 1所示的关系.
|
图 1 耦合微带线上输出与输入信号关系[13] |
图 1所示的耦合微带传输线上输出信号和输入信号的关系也可以用信道传输矩阵来描述,n条耦合传输线的信道传输矩阵为[13]
| $H=\left( \begin{matrix} {{h}_{11}} & {{h}_{12}} & \ldots & {{h}_{1n}} \\ {{h}_{21}} & {{h}_{22}} & \ldots & {{h}_{2n}} \\ \vdots & \vdots & {} & \vdots \\ {{h}_{n1}} & {{h}_{n2}} & \ldots & {{h}_{nn}} \\ \end{matrix} \right)$ | (1) |
分析式(1)可知,CTL-CTM中对角线上的元素是每条传输线上的传递函数,它是频率的函数,其余元素实质上是远端串扰的表现形式,根据远端串扰产生的原因和特点可知,这些元素也是频率的函数,那么信道传输矩阵的每个元素都应该是频率的函数[6],即
| $H=\left( \begin{matrix} {{h}_{11}} & \text{ }{{h}_{12}} & \ldots & {{h}_{1n}} \\ {{h}_{21}} & {{h}_{22}} & \ldots & {{h}_{2n}} \\ \vdots & \vdots & {} & \vdots \\ {{h}_{n1}} & {{h}_{n2}} & \ldots & {{h}_{nn}} \\ \end{matrix} \right)=\left( \begin{matrix} {{f}_{11}}\left( \omega \right) & {{f}_{12}}\left( \omega \right) & \ldots & {{f}_{1n}}\left( \omega \right) \\ {{f}_{21}}\left( \omega \right) & {{f}_{22}}\left( \omega \right) & \ldots & {{f}_{2n}}\left( \omega \right) \\ \vdots & \vdots & {} & \vdots \\ {{f}_{n1}}\left( \omega \right) & {{f}_{n2}}\left( \omega \right) & \ldots & {{f}_{nn}}\left( \omega \right) \\ \end{matrix} \right)$ | (2) |
由于信道传输矩阵表明了耦合传输线上输出信号与输入信号的关系,因此通过信号处理使信道传输矩阵变为单位阵,那么输出信号就等于输入信号,串扰就可以被抵消掉了. 显然,如果在传输线的输出端构造H-1矩阵就可以实现信道传输矩阵为单位阵,从而实现无串扰传输,但由于CTL-CTM为复数矩阵,且其中的每个元素都是频率的函数,根据逆矩阵的求法可知,H-1矩阵中的每个元素仍会是频率的函数,每个元素在电路实现上对应着一个电路,因此H-1完全实现起来会比较复杂,特别是一些元素的数学表达式在电路上不一定能实现,为了简单起见,可以考虑选择合适的矩阵分解方法对H进行分解,化整为零,分块实现H-1.
根据远端串扰产生的原理可知,多条微带传输线中每条传输线受其左右两边相邻传输线的串扰影响最大,因此考虑一组3条微带传输线间的串扰抵消是一个更一般的方案,下一节就来讨论3条微带线间的串扰抵消方案.
2 三条微带线间的串扰抵消方案在一组3条耦合微带传输线上建立信道传输矩阵,假设每条微带传输线上的输入信号为viin(1≤i≤3),输出信号为viout(1≤i≤3),所有端口全部匹配,每条传输线无损耗传输(CTL-CTM中对角线上的元素为1)且只考虑相邻传输线对其的远端串扰,根据文献[13]可知该组传输线上输出信号与输入信号的关系为
| $\left. \begin{matrix} {{v}_{1out}}\approx {{v}_{1in}}-j\Delta kl{{v}_{2in}} \\ {{v}_{2out}}\approx -{{v}_{1in}}j\Delta kl+{{v}_{2in}}-j\Delta kl{{v}_{3in}} \\ {{v}_{3out}}\approx -j\Delta kl{{v}_{2in}}+{{v}_{3in}} \\ \end{matrix} \right\}$ | (3) |
其中:Δk≈ω(Lm+CmZ02)/2Z0,Z0为微带传输线的特性阻抗,Lm为单位长度相邻耦合传输线间的互感,Cm为单位长度相邻耦合传输线间的互容,l 为耦合传输线的长度.
由此可以得到3条微带传输线上的近似信道传输矩阵为
| $H=\begin{matrix} {{f}_{11}}\left( \omega \right){{f}_{12}}\left( \omega \right){{f}_{13}}\left( \omega \right) \\ {{f}_{21}}\left( \omega \right){{f}_{22}}\left( \omega \right){{f}_{23}}\left( \omega \right) \\ {{f}_{31}}\left( \omega \right){{f}_{32}}\left( \omega \right){{f}_{33}}\left( \omega \right) \\ \end{matrix}\text{ }\approx \left( \begin{matrix} 1 & -j\Delta kl & 0 \\ -j\Delta kl & 1 & -j\Delta kl \\ 0 & -j\Delta kl & 1 \\ \end{matrix} \right)$ | (4) |
由上一节的分析可知,此时H-1的构造会比较复杂,电路上也难于实现,因此考虑对复数矩阵H进行EVD分解,然后根据分解形式构造单位阵.
H矩阵的EVD分解形式如式(5)所示,可以看出,EVD分解形式包含2个酉矩阵U、UH和1个对角阵A,这样,只需要对H矩阵分别进行左乘UH和右乘酉矩阵U运算,然后再右乘1个对角阵A-1就可以实现总的信道传输矩阵为单位阵,这一过程如式(6)所示.
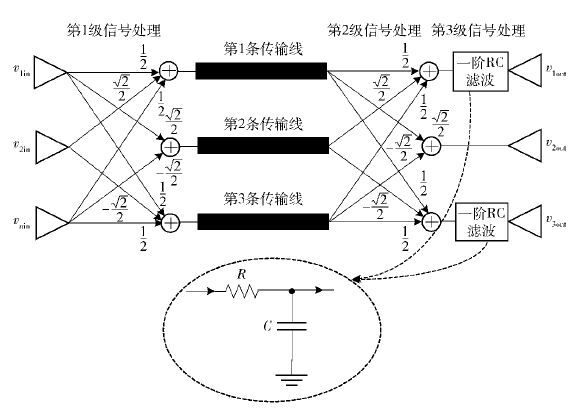
由于酉矩阵和对角阵在电路上易于实现,因此对H矩阵进行EVD分解然后再进行单位阵的构造这一方法克服了H-1难于电路实现的问题. 根据式(6),2个酉矩阵UH和U的元素都是常数,因此在电路实现上非常简单. 然而,对角阵A-1中的元素需要构造相应的电路去实现,分析其元素1/(1+j2Δkl)可知,该式与一阶RC低通滤波电路的传递函数一致,因此可用一阶RC低通滤波电路来实现,而另一元素1/(1-j2Δkl),没有与之一样传递函数的电路,但分析其本质可知其仍然可以用一阶RC低通滤波电路来实现,这样在2条传输线的输出端添加RC低通滤波电路就完成了对角阵A-1的构建,构建结果如式(7)所示. 串扰抵消电路构建后,第2条和第3条传输线上的传递函数为1,实现了信号的无损耗传输,而第1条传输线上的传递函数为(1-j2Δkl)/(1+j2Δkl),由于这个传递函数表现为全通系统的特点,因此不会产生幅度衰减和畸变,能保证信号的无损耗传输. 这样所提方法在3条耦合传输线上都实现了无串扰传输,具体电路实现方案如图 2所示,2个酉矩阵对应第1级信号处理和第2级信号处理,一阶RC滤波电路对应于第3级信号处理.
| $\begin{align} & H=\left( \begin{matrix} 1 & -j\Delta kl & 0 \\ -j\Delta kl & 1 & -j\Delta kl \\ 0 & -j\Delta kl & 1 \\ \end{matrix} \right)=UA{{U}^{H}}=\left( \begin{matrix} \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} \\ \frac{\sqrt{2}}{2} & 0 & -\frac{\sqrt{2}}{2} \\ \frac{1}{2} & -\frac{\sqrt{2}}{2} & \frac{1}{2} \\ \end{matrix} \right) \\ & \left( \begin{matrix} 1-j\sqrt{2}\Delta kl & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1+j2\Delta kl \\ \end{matrix} \right)\times \left( \begin{matrix} \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} \\ \frac{\sqrt{2}}{2} & 0 & -\frac{\sqrt{2}}{2} \\ \frac{1}{2} & -\frac{\sqrt{2}}{2} & \frac{1}{2} \\ \end{matrix} \right) \\ \end{align}$ | (5) |
| $\begin{align} & {{U}^{H}}HU{{A}^{-1}}=\left( \begin{matrix} \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} \\ \frac{\sqrt{2}}{2} & 0 & -\frac{\sqrt{2}}{2} \\ \frac{1}{2} & -\frac{\sqrt{2}}{2} & \frac{1}{2} \\ \end{matrix} \right)\times \left( \begin{matrix} 1 & -j\Delta kl & 0 \\ -j\Delta kl & 1 & -j\Delta kl \\ 0 & -j\Delta kl & 1 \\ \end{matrix} \right)\text{ } \\ & \left( \begin{matrix} \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} \\ \frac{\sqrt{2}}{2} & 0 & -\frac{\sqrt{2}}{2} \\ \frac{1}{2} & -\frac{\sqrt{2}}{2} & \frac{1}{2} \\ \end{matrix} \right)\times \left( \begin{matrix} \frac{1}{1-j\sqrt{2}\Delta kl} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \frac{1}{1+j\sqrt{2}\Delta kl} \\ \end{matrix} \right)=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right) \\ \end{align}$ | (6) |
|
图 2 3条耦合微带线上串扰抵消的电路方案 |
| $\begin{align} & \left( \begin{matrix} \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} \\ \frac{\sqrt{2}}{2} & 0 & -\frac{\sqrt{2}}{2} \\ \frac{1}{2} & -\frac{\sqrt{2}}{2} & \frac{1}{2} \\ \end{matrix} \right)\left( \begin{matrix} 1 & -j\Delta kl & 0 \\ -j\Delta kl & 1 & -j\Delta kl \\ 0 & -j\Delta kl & 1 \\ \end{matrix} \right)\text{ }\times \left( \begin{matrix} \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} \\ \frac{\sqrt{2}}{2} & 0 & -\frac{\sqrt{2}}{2} \\ \frac{1}{2} & -\frac{\sqrt{2}}{2} & \frac{1}{2} \\ \end{matrix} \right) \\ & \left( \begin{matrix} \frac{1}{1-j\sqrt{2}\Delta kl} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \frac{1}{1+j\sqrt{2}\Delta kl} \\ \end{matrix} \right)=\left( \begin{matrix} \frac{1-j\sqrt{2}\Delta kl}{1+j\sqrt{2}\Delta kl} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right) \\ \end{align}$ | (7) |
由于一阶RC低通滤波电路的传递函数为
| ${{H}_{RC}}\left( \omega \right)=\frac{1}{1+j\omega RC}$ | (8) |
所以,图 2中一阶RC低通滤波电路的参数可以通过式(9)来确定.
| $\frac{1}{1+j\omega RC}=\frac{1}{1+j2\Delta kl}~$ | (9) |
即
| $RC=\frac{\sqrt{2}l}{2{{Z}_{0}}}({{L}_{m}}+{{C}_{m}}{{Z}^{2}}_{0})$ | (10) |
类比MIMO系统可知,只要传输线的物理结构确定了,不管其物理结构什么样都存在着信道传输矩阵(只是物理结构会影响信道传输矩阵构建的难度),因此,所提的串扰抵消方法允许降低传输线间的间距,线间距的降低可以增加电路板的有效面积,提高吞吐量,可以克服从传输线物理结构角度减小串扰方法不能降低线间距的瓶颈.
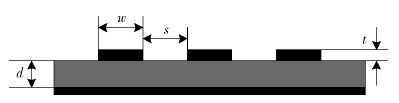
3 仿真与结果分析本节利用先进设计系统(ADS,advanced design system)软件仿真验证所提方法的有效性. 调用软件TLines-Microstrip中的MACLIN3创建了3条平行微带传输线,如图 3所示,具体参数:微带线宽w=40 mil,微带线间距s=40 mil,介质高度d=22 mil,微带线导体厚度t=70 μm,介质相对介电常数εr=4.5,相对磁导率μr
|
图 3 仿真中的3条平行微带线参数图 |

|
图 4 眼图仿真结果对比 |
仿真结果如图 4所示,从中可以看出,3条传输线上几乎闭合了的眼图都恢复了较好的质量,由于第2条传输线的输出端不需要进行第3级的信号处理,因此其上眼图质量恢复最好,而另外2条传输线眼图恢复质量稍差,主要原因有如下几点:第一,在这2条传输线的输出端都进行了一阶RC低通滤波,RC低通滤波电路无法实现与传输线的理想阻抗匹配;第二,为了简便起见,在建立CTL-CTM时没有考虑第1条传输线和第3条传输线之间的串扰;第三,在建立CTL-CTM时,其中相邻传输线间的串扰是近似值,未考虑二次串扰. 尽管存在这些因素致使眼图恢复质量稍差,但相对于未使用所提方法前,眼图仍有非常明显的改善.
以上仿真验证了所提方法抑制3条传输线间串扰的有效性. 在50 Ω总线中,当线间距等于线宽时,如果只考虑受扰线受其左右两侧各1条干扰线串扰,此时串扰占总串扰的75%;如果考虑其左右两侧各2条干扰线的串扰,此时串扰占比将达到95%[2]. 因此,从代价与效果折衷的角度出发考虑受扰线左右两侧各2条干扰线的串扰将是一个比较合适的选择,即此时的信道传输矩阵为5阶矩阵. 当H为5阶矩阵时,其中的元素数量及复杂程度都远高于3阶矩阵,矩阵的阶数增加,对其处理的运算量是非线性增长的,如果对其直接进行EVD分解,得到的元素组成也会更复杂,对应的电路也难于物理实现. 为了解决这一问题需要在矩阵分解前对其中的元素进行简化,然后再根据矩阵分解形式进行电路设计,如何简化,简化到什么程度这需要深入研究.
4 结束语在对多条耦合微带传输线信道传输矩阵进行EVD分解的基础上,提出了用于一组3条耦合微带传输线上串扰抵消的方法,该方法在微带传输线的输入端和输出端分别进行相应的信号处理,实现了串扰抵消. ADS软件仿真结果显示,这种方法能明显改善信号眼图的质量,并且在电路实现上比较简单,能够以较低代价获取较好的串扰抵消效果,且该方法允许降低传输线间的间距,这有助于提高电路的密度,从而增加电路板的有效面积.
| [1] |
Fan Jun, Ye Xiaoning, Kim J, et al. Signal integrity design for high-speed digital circuits:progress and directions[J]. IEEE Transactions on Electromagnetic Compatibility , 2010, 52 (2) :392–400.
doi:10.1109/TEMC.2010.2045381 ( 0) 0)
|
| [2] |
Bogatin E.
Signal integrity-simplified[M]. New Jersey: Prentice Hall , 2004 .
( 0) 0)
|
| [3] |
Halligan M S, Beetner D G. Maximum crosstalk estimation in weakly coupled transmission lines[J]. IEEE Transactions on Electromagnetic Compatibility , 2014, 56 (3) :736–743.
doi:10.1109/TEMC.2014.2304735 ( 0) 0)
|
| [4] |
王亚飞. 高速高密度总线系统中串扰抵消技术研究[D]. 北京:北京邮电大学, 2013.
http://cdmd.cnki.com.cn/article/cdmd-10013-1015528661.htm ( 0) 0)
|
| [5] |
Lee K, Lee H B, Jung H K, et al. Serpentine microstrip line with zero far-end crosstalk for parallel high-speed DRAM interfaces[J]. IEEE Transactions on Advanced Packaging , 2010, 33 (2) :552–558.
doi:10.1109/TADVP.2009.2033938 ( 0) 0)
|
| [6] |
安静, 武俊峰, 吴一辉. 使用防护带抑制微带线间串扰的研究[J]. 北京理工大学学报 , 2011, 31 (3)
:343–347.
An Jing, Wu Junfeng, Wu Yihui. Research of suppressing crosstalk of the microstrip lines by using stripe protection[J]. Journal of Beijing Institute of Technology , 2011, 31 (3) :343–347.
( 0) 0)
|
| [7] |
Wu Boping, Mo Tingting Barbed transmission lines for crosstalk suppression[C]//2012 Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC). Sentosa:IEEE Press, 2012:621-624.
( 0) 0)
|
| [8] |
Kachout M, Bel Hadj Tahar J, Choubani F. Three conductors non uniform transmission lines:electrical equivalent model & crosstalk reduction[C]//2014 International Conference on Multimedia Computing and Systems (ICMCS). Marrakech:IEEE Press, 2014:1376-1379.
( 0) 0)
|
| [9] |
孙绪印, 林志立, 欧攀, 等. 微带线间远端串扰的电磁仿真研究[J]. 计算机应用研究 , 2014, 31 (9)
:2665–2667.
Sun Xuyin, Lin Zhili, Ou Pan, et al. Study of far-end crosstalk between microstrip lines with electromagnetic simulation[J]. Application Research of Computers , 2014, 31 (9) :2665–2667.
( 0) 0)
|
| [10] |
Xu Jun, Wang Shuo. Investigating a guard trace ring to suppress the crosstalk due to a clock trace on a power electronics DSP control board[J]. IEEE Transactions on Electromagnetic Compatibility , 2015, 57 (3) :546–554.
doi:10.1109/TEMC.2015.2403289 ( 0) 0)
|
| [11] |
Taehyoun O, Harjani R. A 6-Gbit/s MIMO crosstalk cancellation scheme for high-speed I/Os[J]. IEEE Journal of Solid-State Circuits , 2011, 46 (8) :1843–1856.
doi:10.1109/JSSC.2011.2151410 ( 0) 0)
|
| [12] |
Taehyoun O, Harjani R. A 12-Gbit/s multichannel I/O using MIMO crosstalk cancellation and signal reutilization in 65-nm CMOS[J]. IEEE Journal of Solid-State Circuits , 2013, 48 (6) :1383–1307.
doi:10.1109/JSSC.2013.2252517 ( 0) 0)
|
| [13] |
Wang Yafei, Li Xuehua. Crosstalk cancellation method based on unitary transformation of coupled transmission lines-channel transmission matrix[J]. Progress in Electromagnetics Research Letters , 2015, 52 :45–50.
doi:10.2528/PIERL15011602 ( 0) 0)
|


