2. 西安邮电大学 通信与信息工程学院, 西安 710061
为了在提升用户吞吐量的同时降低中继节点切换概率,分析了动态场景下用户与中继节点的移动状态,提出了多目标联合优化的移动中继选择策略.算法通过分析动态场景中影响系统吞吐量与中继切换概率的因素进行中继节点选择,充分考虑了多跳蜂窝网络的移动特性和用户呼叫到达状态.仿真结果表明,所提算法在有效提升用户吞吐量的同时降低了中继切换概率.
2. The School of Telecommunication and Information Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710061, China
The mobile relay selection problems in multi-hop cellular network are studied. The selection of mobile relay affects such performances as the throughput of the system, spectral efficiency and relay switching probability. In order to improve the throughput and reduce the relay switching probability, the mobile state of the users and the relay nodes in the dynamic scenario was analyzed, then a multi-objective joint optimization based mobile relay selection scheme was proposed. The scheme analyzes two factors which affect the system throughput and the relay switching probability in dynamic scenario. The mobile characteristic of multi-hop cellular network and the state of users' call arrival are taken into full consideration. Simulation shows that the algorithm can improve the users' throughput effectively and reduce the relay switching probability.
随着通信技术的飞速发展,中继技术作为解决无线网络覆盖扩展以及速率提升两大挑战的有效技术,受到国内外学者的广泛关注[1]. 未来的5G网络将会考虑用户与用户之间的通信,该项技术能在一定程度上扩展网络覆盖,解决系统频谱资源匮乏等问题[2-3].
一些学者从回程链路(BL,backhaul link)及接入链路(AL,access link)的距离入手,综合考虑中继节点与基站以及中继节点与用户的相对位置关系,提出了基于距离的算法,旨在提升系统的吞吐量[4]. 唐伦等[5]提出了基于信干噪比(SINR,signal to interference and noise ratio)进行中继选择的双向中继选择策略(BRS,bidirectional relaying strategy). Zhu等[6]考虑了用户服务质量和网络能量节约,提出了一种在中继蜂窝网络中的动态能量控制算法. 这些选择算法多是在静态场景中分析,很少考虑中继及用户位置的移动带来的影响,实际上,中继节点的移动必然引起用户通信状况的改变. 提升系统吞吐量与降低中继切换概率一直是困扰着移动中继选择技术的两大难题,Zhang等[7]提出了一种以降低切换概率为目的,基于中继服务时长的移动中继选择算法(so-MBRSC,suboptimal solution mobilebased relay selection schemes). 目前的研究多是针对单个用户如何选择中继节点进行分析,而网络边缘区域需要通过中继进行通信的用户往往不止一个,因此,在动态场景中分析用户与中继节点的通信状态及运动情况,以提升系统整体吞吐量同时降低中继切换次数为目标,提出了动态场景中多目标联合优化的移动中继选择策略. 以蜂窝小区场景为例,但应用场景并不局限于蜂窝小区.
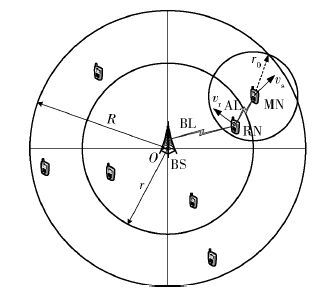
1 动态场景中基于多目标中继选择策略如图 1所示,信道质量好的移动节点(MN,mobile node)与基站(BS,base station)直接进行通信,被称为一跳用户. 质量较差的用户尤其是边缘用户,选择信道质量好的用户作为中继节点与基站进行间接通信,该用户被称为两跳用户. 移动节点在小区内移动模型通常有2种:第1种为随机移动模型(RWM,random walk mobility);第2种为无边界移动模型(BAM,boundless area mobility][8]. 文中用户移动模型采用无边界移动模型.
|
图 1 边缘区用户移动模型 BS为基站,MN为移动用户,RN为中继用户BL为回程链路,AL为接入链路 |
多目标中继选择策略是针对提升用户吞吐量与降低中继切换概率两个目标进行中继节点的选择,因此中继选择的指标可以归结为两部分:第一,影响切换概率的因素;第二,影响吞吐量的因素. 基于多目标的中继节点选择策略是通过计算备选中继在通信区域内的停留时间来进行切换概率的预测,通过调节接入链路和回程链路的带宽来进行吞吐量的预测.
1.1 切换概率因素预测1) 切换概率的分析
考虑用户呼叫到达满足参数为λ的泊松分布,呼叫间隔满足均值为1/λ的指数分布,用户的服务时间满足参数为μ的指数分布,即平均服务时长为1/μ.
图 1中,BS位置坐标为O(0,0),传输距离为R,中心区域半径为r,用户通信范围为r0. 在用户通信过程中,中继节点移出用户通信范围与中心区域交叉区域,即通信时长大于中继节点在交叉区域内的停留时间时,需要发生中继切换,该条件下的切换概率Ph(1)满足如下条件:
| ${{P}^{(1)}}_{h}=P({{t}_{a}}>{{t}_{m}})={{\int }^{_{\infty }}}_{{{t}_{m}}}\mu {{e}^{-\mu {{t}_{a}}}}d{{t}_{a}}={{e}^{-\mu {{t}_{m}}}}$ | (1) |
其中:tm为中继节点停留在交叉区域的时间,ta为中继节点忙碌时间.
在用户通信过程中,中继节点有呼叫到达时,即用户的通信时间大于中继空闲时间,需要中继切换,该条件下切换概率Ph(2)为
| ${{P}^{(2)}}_{h}=P({{t}_{a}}>{{t}_{i}})={{\int }^{_{\infty }}}_{0}{{\int }^{_{\infty }}}_{{{t}_{i}}}\mu {{e}^{-\mu {{t}_{a}}}}\lambda {{e}^{-\lambda {{t}_{i}}}}d{{t}_{a}}d{{t}_{i}}=\frac{\lambda }{\lambda +\mu }$ | (2) |
其中ti为中继节点空闲时间.
综合以上分析可知,中继总切换概率Ph用以下公式表示:
| ${{P}_{h}}={{P}^{(1)}}_{h}+{{P}^{(2)}}_{h}=\frac{\lambda }{\lambda +\mu }+{{e}^{-\mu {{t}_{m}}}}~$ | (3) |
对函数关于t求导得
| $P{{\prime }_{h}}({{t}_{m}})=\frac{d{{P}_{h}}}{d{{t}_{m}}}=-\mu {{e}^{-\mu {{t}_{m}}}}$ | (4) |
其中,由tm>0 ,μ>0知P′h(tm)<0,Ph为关于tm的递减函数. 可知,当tm取最大值时,Ph值最小. 故中继切换概率与tm成反比. 又切换概率因素与切换概率成反比,为此,对切换概率因素的预测等价于预测tm大小.
2) 切换概率预测
移动节点的工作状态有忙碌(active)与空闲(idle)两种. 当节点有信息到达时状态为忙碌,当节点没有信息到达时为空闲. 图 1中,初始时刻,边缘用户坐标为(xm,ym),速度为(vm,θm);假定选中的中继节点坐标为(xr,yr),速度为(vr,θr);DOM(t)表示两跳用户到基站之间距离,DOR(t)表示中继到基站之间距离,DRM(t)表示用户到中继之间距离. 状态经过时间t之后,基站-中继-两跳用户的相对位置及通信状态均可能发生变化. 当DOR(t) >r,DRM(t)>r0或者中继节点变为忙碌状态时,发生中继切换. 经过t时刻用户的坐标为(xm+vmtcos θm,ym+vmtsin θm),中继节点的坐标变为(xr+vrtcos θr,yr+vrtsin θr). 假设t1为中继节点离开基站通信范围的临界值,t2为中继节点离开用户通信范围的临界值. 分析图 1用户移动模型可知,
| ${{D}_{OR}}({{t}_{1}})=\sqrt{{{({{x}_{r}}+{{v}_{r}}{{t}_{1}}cos~{{\theta }_{r}})}^{2}}+{{({{y}_{r}}+{{v}_{r}}{{t}_{1}}sin~{{\theta }_{r}})}^{2}}}=r~$ | (5) |
分析图 1可知,当中继节点速度方向确定后,中继节点在交叉区域内到达中心区域边界的时间为正值,通过解方程(5)取正值得到t1.
| ${{t}_{1}}=\frac{-({{x}_{r}}cos~{{\theta }_{r}}+{{y}_{r}}sin~{{\theta }_{r}})+\sqrt{{{r}^{2}}-{{({{x}_{r}}sin~{{\theta }_{r}}-{{y}_{r}}cos~{{\theta }_{r}})}^{2}}}}{{{v}_{r}}}$ | (6) |
求解t2时,可以将用户看作不动的点,中继节点相对于用户移动速度为(vrl,θrl),相对坐标为(xrl,yrl),则它们可以表示为
| ${{x}_{rl}}={{x}_{r}}-{{x}_{m}}{{y}_{rl}}={{y}_{r}}-{{y}_{m}}$ | (7) |
| $\left. \begin{matrix} {{v}_{rl}}=\sqrt{{{({{v}_{r}}cos{{\theta }_{r}}-{{v}_{m}}cos{{\theta }_{m}})}^{2}}+{{({{v}_{r}}sin{{\theta }_{r}}-{{v}_{m}}sin{{\theta }_{m}})}^{2}}} \\ {{\theta }_{rl}}=arctan\frac{{{v}_{r}}sin{{\theta }_{r}}-{{v}_{m}}sin{{\theta }_{m}}}{{{v}_{r}}cos{{\theta }_{r}}-{{v}_{m}}cos{{\theta }_{m}}}\pm \pi \\ \end{matrix} \right\}$ | (8) |
类似于t1的求解过程,可得出
| ${{t}_{2}}=-\frac{({{x}_{rl}}cos~{{\theta }_{rl}}+{{y}_{rl}}sin~{{\theta }_{rl}})}{{{\nu }_{rl}}}+\frac{\sqrt{{{r}^{2}}_{0}-{{({{x}_{rl}}sin~{{\theta }_{rl}}-{{y}_{rl}}cos~{{\theta }_{rl}})}^{2}}}}{{{\nu }_{rl}}}~$ | (9) |
准确预测t1、t2的大小,可以有效降低中继切换概率,但即便目前的智能装置都配有GPS模块,也很难定位每一时刻移动节点速度的方向与大小,为此,需要对中继选择算法进行优化,用t1、t2的期望值代替其本身,不仅可以降低对设备的要求,也可以降低算法复杂度. 文献[7]中也给出了求解t1、t2期望值的分析,然而文献[7]中所提算法并没有结合场景中的实际情况进行考虑,下面将给出笔者所提方法与文献中分析的对比.
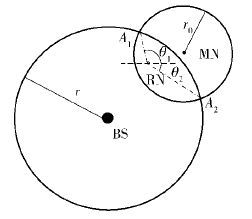
如图 2所示,用户通信范围与中心区域交点为A1、A2,中继节点RN与两交点相连,与水平方向所成角度分别为θ1、θ2.
|
图 2 中继区域示意图 |
当θ2 <θr<θ1+2π时,中继节点移出用户通信范围与中心区域交叉区域的边界条件为:x2+y2=r2,因为节点的运动方向随机分配,速度大小满足[Vmin,Vmax]上的均匀分布,则t1的期望如下:
| ${{T}_{1}}=E({{t}_{1}})=\frac{1}{(2\pi +{{\theta }_{1}}-{{\theta }_{2}})({{V}_{max}}-{{V}_{min~}})}{{\int }^{{{V}_{max~}}}}_{{{V}_{min}}~}{{\int }^{2\pi +{{\theta }_{1}}}}_{{{\theta }_{2}}}{{t}_{1}}d{{\theta }_{r}}d{{v}_{r}}$ | (10) |
当θ1 <θrl<θ2时,中继节点移出用户通信范围与中心区域交叉区域的边界条件为:(x-xm)2+(y-ym)2=r0,中继相对与用户的速度大小在[0,2Vmax]上均匀分布,则t2的期望为
| ${{T}_{2}}=E({{t}_{2}})=\frac{1}{2{{V}_{max~}}({{\theta }_{2}}-{{\theta }_{1}})}{{\int }^{2{{V}_{max~}}}}_{0}{{\int }^{{{\theta }_{2}}}}_{{{\theta }_{1}}}{{t}_{2}}d{{\theta }_{rl}}d{{v}_{rl}}$ | (11) |
式(10)、式(11)中Vmax、Vmin为系统常量,可根据情况设置多组参数进行分析,得出算法性能与用户速度关系;θ1、θ2可根据用户坐标及通信链路直径r0求得. 用tm表示tm的数学期望,则tm的预测值为
| ${{T}_{m}}\left( i \right)=min~[{{T}_{1}}\left( i \right),{{T}_{2}}\left( i \right)]$ | (12) |
式(12)中,T1(i)为备选中继集内第i个中继节点离开交叉区域基站通信范围的平均时间;T2(i)为备选中继集内第i个中继节点离开交叉区域用户通信范围的平均时间.
切换概率因素与备选中继切换概率成反比,与所有备选中继切换概率均值成正比,则切换概率因素与中继在交叉区域停留时间tm成正比,与所有备选中继(假定数量为n)tm的均值成反比. 为了做定性分析,选取t时刻第k个备选中继停留时间归一化Sk(t)作为t时刻第k个备选中继的切换判决因子,则Sk(t)的表达式为:
| ${{S}_{k}}\left( t \right)=\frac{{{T}^{k}}_{m}\left( t \right)}{\frac{1}{n}\sum\limits_{i=1}^{n}{{{T}^{i}}_{m}\left( t \right)}}$ | (13) |
其中:Tmk(t)为t时刻,第k个中继在交叉区域停留时间的预测值,
链路传输速率由链路带宽及信道状况共同决定,由香农公式得链路传输速率表达式为
| $\left. \begin{matrix} {{\gamma }_{a}}={{B}_{a}}lb(1+{{C}_{a}}) \\ {{\gamma }_{b}}={{B}_{b}}lb(1+{{C}_{b}}) \\ \end{matrix} \right\}$ | (14) |
其中:γa为AL上的传输速率,γb为BL上的传输速率,Ba为两跳用户AL上分得的带宽,Bb为两跳用户BL上分得的带宽,Ca为两跳用户AL的信干噪比,Cb为两跳用户BL的信干噪比,备选中继对应链路传输速率预测的核心是,通过调节Ba与Bb的分配,使得γa=γb.
将备选中继k对应链路信号传输速率记为γk,则所有备选中继(假设总数为n)的吞吐量均值计算公式为
| $\bar{\gamma }=\frac{1}{n}\sum\limits_{k=1}^{n}{{{\gamma }_{k}}}$ | (15) |
由于吞吐量因素与单个备选中继对应链路传输速率成正比,与所有备选中继对应链路传输速率均值成反比,又因为动态场景中,链路信道状态与所得带宽随时间变化,为了做定性分析,选取t时刻第k个备选中继的吞吐量归一化hk(t)作为t时刻第k个备选中继的吞吐量判决因子,则hk(t)的表达式为
| ${{h}_{k}}\left( t \right)=\frac{{{\gamma }_{k}}\left( t \right)}{{\bar{\gamma }}}\text{ }$ | (16) |
其中:γk(t)为t时刻第k个中继的的链路传输速率,γ为t时刻n个备选中继的吞吐量均值. γk(t)越大,hk(t)越大,t时刻第k个备选中继越可能被选作最优中继.
1.3 多目标中继选择算法吞吐量因子与切换概率因子均能影响中继节点的选择,由式(13)知,切换概率因子与中继在交叉区域停留时间有关,停留时间期望值越大,中继节点优先级越高;由式(16)知,吞吐量因子与链路实时传输速率成正比,链路传输速率越高,中继节点优先级越高. 由于吞吐量与切换概率的单位不同,两者的数量级也差别较大,为此,利用对数归一化思想,构建起关于吞吐量因子与切换概率因子的中继选择判决函数,如式(17)所示:
| ${{F}_{k}}\left( t \right)=\alpha lb{{h}_{k}}\left( t \right)+\beta lb{{S}_{k}}\left( t \right)=\alpha lb\frac{{{\gamma }_{k}}\left( t \right)}{\frac{1}{n}\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\gamma }_{i}}\left( t \right)}+\beta lb\frac{{{T}^{k}}_{m}\left( t \right)}{\frac{1}{n}\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{T}^{i}}_{m}\left( t \right)}$ | (17) |
其中:Fk(t)为备选中继节点k在t时刻的综合判决因子;n为备选中继集合内元素个数;α、β分别为吞吐量因子的调整系数和切换概率因子的调整系数,取值范围均为[0,1],且α+β=1.
通过对比判决因子Fk(t)的大小,选出判决因子最大时对应的备选中继,即为两跳用户i的最优中继:
| $Pr{{~}_{i}}\left( R \right)=\underset{k\in \left\{ 1,\ldots ,n \right\}}{\mathop{arg~max}}\,~\{{{F}_{k}}\left( t \right)\}$ | (18) |
其中Pr i(R)为两跳用户i对应的最优中继.
由式(17)知Fk(t)为一个无量纲数值,数值大小由中继节点的吞吐量因子与切换概率因子共同决定,通过调整α、β的比值可以调节两个因素在决策函数中的权重,满足不同网络环境下对吞吐量与切换概率的要求.
2 算法性能仿真分析模拟蜂窝小区环境进行对多目标中继选择策略进行仿真. 其中小区半径R=1 000 m,用户通信范围r0=150 m,系统资源块总数100块,基站发射功率PBS=40 W,中继用户发射功率PMN=250 mW,基站天线增益GBS=15 dBi,平均服务时长1/μ=100 s,平均空闲时长1/λ=1 000 s,边缘区内用户数目[100,900],载频fc=2 GHz,系统带宽B=20 MHz,噪声功率谱密度Npsd=-174 dBm/Hz,小区间平均干扰功率Pai=-70 dBm. 利用上述参数对多目标中继选择算法进行了仿真,从用户总吞吐量和切换次数方面与传统中继节点选择算法进行了对比.
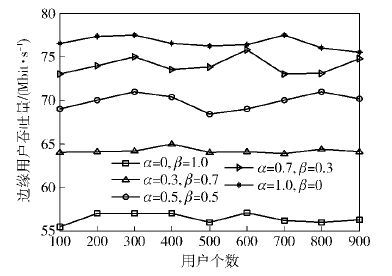
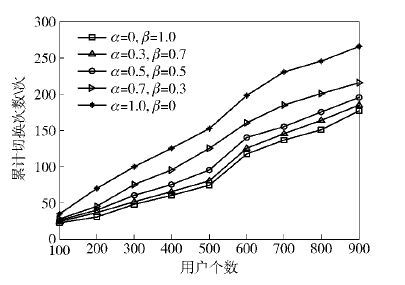
图 3和图 4是当用户的最大移动速度V=10 m/s,α和β取多组值时的仿真图. 由图 3仿真结果可看出,随着α的增大,用户吞吐量增大,α越大,多目标中继选择策略越接近吞吐量预测算法. α=1时,相当于增强吞吐量因子算法,吞吐量达到最大. 由图 4仿真结果可以看出,β越大,用户切换次数越少,β越大,多目标中继选择策略越接近切换概率预测算法. β=1时,相当于增强切换概率算法,此时,切换次数最小. 多目标中继选择策略进行综合考虑之后,在保证中继切换概率不高的前提下,为有效提升用户吞吐量,将α适当取得大一些,α=0.7,则β=0.3.
|
图 3 边缘区用户吞吐量随α、β、用户数变化 |
|
图 4 边缘区用户切换概率随α、β、用户数变化 |
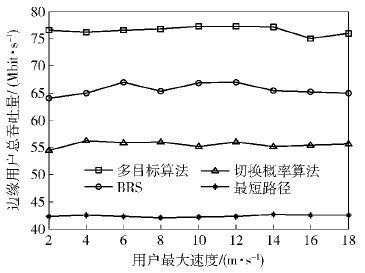
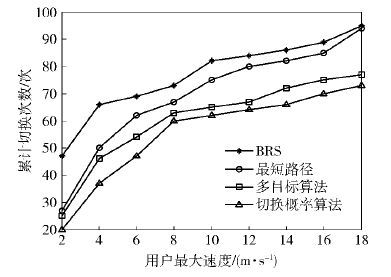
图 5和图 6所示为用户个数为200、用户最大移动速度变化时的仿真结果. 由图 5仿真结果可知,由于系统内数目不变,两跳用户的数目按照一定的比例分布,大体上不会发生很大变化,因此,随着速度变化用户吞吐量基本保持不变. 最短路径算法以两条链路路径最小选择最优中继,仅仅考虑了路径距离,切换概率算法从降低切换次数出发,并未直接考虑用户通信速率,因此这两种算法对用户吞吐量提升不够明显;经典双向中继选择策略(BRS,bidirectional relaying strategy)算法以链路信干噪比为选择指标,且考虑了瓶颈链路对通信质量的影响,对用户吞吐量提升比较明显;多目标中继选择策略,在吞吐量因素方面不仅考虑了链路信干噪比,而且考虑了带宽对传输速率的影响,对吞吐量提升最为明显. 由图 6仿真结果可知,随着移动速度的增大中继节点切换次数增加. 由于基站与用户通信范围一定,中继可以为两跳用户提供服务的区域范围大小是固定的,因此随着用户及中继节点移动速度的提升,中继节点更容易离开服务范围,中继切换次数增加. 4种算法对应的中继节点切换次数,经典BRS算法最多,切换概率算法最低,多目标中继选择策略与切换概率算法效果相差不大. 在多组移动速度下,多目标中继选择算法不仅提升了用户吞吐量而且有效降低了中继切换次数,与算法预期效果一致.
|
图 5 边缘区用户总吞吐量随最大速度变化 |
|
图 6 边缘区用户累计切换次数随最大速度变化 |
针对动态环境下中继选择问题,提出了基于多目标联合优化的中继选择策略. 详细分析了动态场景下,用户与中继节点的位置变化对系统性能产生的影响,将降低切换概率与提升用户吞吐量两个目标进行结合,提出了基于多目标的中继节点选择策略. 与传统的中继选择算法相比,有效降低了中继切换次数,同时提升了用户吞吐量.
| [1] |
Sydir J, Taori R. An evolved cellular system architecture incorporating relay stations[J]. IEEE Communications Magazine , 2009, 47 (6) :115–121.
doi:10.1109/MCOM.2009.5116808 ( 0) 0)
|
| [2] |
曲桦, 庄雄, 赵季红, 等. 蜂窝网络下设备到设备通信中的联合资源优化[J]. 北京邮电大学学报 , 2015, 38 (3)
:112–116.
Qu Hua, Zhuang Xiong, Zhao Jihong, et al. Joint resource optimization of equipment to equipment communication in a cellular network[J]. Journal of Beijing University of Posts and Telecommunications , 2015, 38 (3) :112–116.
( 0) 0)
|
| [3] |
Tang Rui, Zhao Jihong, Qu Hua. Joint optimization of channel allocation, link assignment and power control for device-to-device communication underlying cellular network[J]. China Communications , 2015, 12 (12) :92–100.
doi:10.1109/CC.2015.7385517 ( 0) 0)
|
| [4] |
Wang L C, Su W S, Huang J H, et al. Optimal relay location in multi-hop cellular systems[C]//WCNC. Las Vegas, NV:IEEE, 2008:1306-1310.
( 0) 0)
|
| [5] |
唐伦, 刘通, 陈前斌, 等. Two-way中继系统协作节点选择及功率分配策略[J]. 电子与信息学报 , 2010, 32 (9)
:2077–2082.
Tang Lun, Liu Tong, Chen Qianbin, et al. Cooperative node selection and power allocation strategy in two-way relay system[J]. Journal of Electronics & Information Technology , 2010, 32 (9) :2077–2082.
( 0) 0)
|
| [6] |
Zhu Yutao, Zeng Zhimin, Zhang Tianhui, et al. A QoS-aware adaptive access point sleeping in relay cellular networks for energy efficiency[C]//Vehicular Technology Conference (VTC Spring) 2014 IEEE 79th. Seoul:IEEE, 2015:1-5.
( 0) 0)
|
| [7] |
Zhang Hao, Hong Peilin, Xue Kaiping. Mobile-based relay selection schemes for multi-hop cellular networks[J]. Communications and Networks , 2013, 15 (1) :45–53.
doi:10.1109/JCN.2013.000009 ( 0) 0)
|
| [8] |
Davies V. A survey of mobility models for Ad hoc network research[J]. Wireless Communication and Mobile Computing (WCMC):Special issue on Mobile Ad Hoc Networking:Research, Trends and Applications , 2002, 2 (5) :483–502.
( 0) 0)
|


