针对海量实时数据流,提出了一种基于密度和网格划分相结合的聚类算法.首先对数据空间进行划分,判断每个单元格中数据点的属性.如果单元格内数据点密度高于阈值,则判定这些点为核心点;否则,根据单元格邻居内数据点的数量对数据点进行再次判断,以确定单元格内的数据点是边界点还是噪声点.算法克服了基于密度的算法运行效率低的缺点,又弥补了基于网格的算法精度较低的不足.通过实验验证了算法的效率和性能,并与经典的DBSCAN和CLIQUE算法进行了对比分析.最后分析了算法在面向海量实时数据流方面所具有的优势,并提出了进一步的研究方向.
The energy efficient and real-time data collecting problem in wireless sensor network was studied. The mobile data collecting protocol consists four phases:nodes clustering, routes planning, routes combine and data collecting is proposed. Two heuristic algorithms save and nearest neighbor were presented to build data collecting routes which incur the least mobile cost while satisfy the deadline constraint. Simulations show that the proposed heuristic routes planning algorithms have good performance in terms of energy saving, deadline guarantee and travel cost reduction.
数据聚类算法是数据流异常分析的基础[1]. 常见的聚类分析算法有层次法、划分法、密度算法、网格算法和模型算法等,基于密度的聚类算法能够适应于任意形状的数据集且抗噪声能力强,因此得到了广泛应用,DBSCAN[2]、OPTICS[3]和DENCLUE[4]都是基于密度的算法. DBSCAN和OPTICS在数据量较大的情况下,运行效率低下;DENCLUE是DBSCAN的一般化形式,因此同样存在计算量较大的缺陷.
基于网格的聚类算法主要有STING[5]和CLIQUE[6]等,它们增加了系统存储代价,而且降低了聚类的质量. CLIQUE虽然是一种基于网格的聚类算法,却很好地结合了密度聚类的思想,但是不能自动去除数据集中的噪声点,这一不足对于异常检测而言是无法接受的. WaveCluster[7]是另外一种基于网格的聚类算法,主要优点是聚类速度非常快,能够发现不同精度的聚类,而且可以自动排除噪声点.
在上述算法中,都将分割后的单元格作为数据点进行处理,参数M用于判断一个网格单元是否是高密度网格单元,当一个网格单元中的数据点数目超过M时,它被认为是一个高密度网格单元,这无疑将导致算法精度的下降. 如图 1所示,如果定义M为4,单元格U的邻居中不存在稠密单元格,但在点a的邻域范围内存在多于4个邻居点,因此a仍然属于核心点. 而在上述算法中,a被处理为噪声或者边界点.
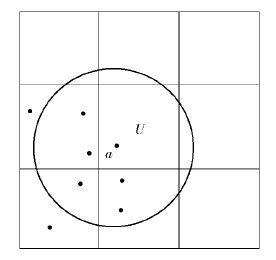
|
图 1 误判单元格示意图 |
笔者提出了一种新颖的聚类算法,结合基于密度和基于网格算法的优点,借鉴图像处理方法中滤波算法的思想,具有较低的运算复杂度,并且易于并行化,能够应用于某些海量实时数据流的异常检测.
1 问题描述所提算法基于DBSCAN,涉及DBSCAN中的两个重要概念:邻域范围半径E和最小邻居阈值M. 在DBSCAN中,根据基于密度的思想和定义,空间数据点可以定性描述为3类:密集区域内部的点,即核心点;密集区域边缘上的点,即边界点;稀疏区域内的点,即噪声点. 因为聚类结果中不包含任意孤立点或噪声,这一过程也可以逆向理解,即如果去除数据集合中的噪声点,得到的集合即为聚类结果. 为简化描述,以二维空间为例,对问题进行分析.
如果将全部数据点在二维平面上的分布呈现出来,则会得到一个散点图. 图 2为微软研究院T-Driver项目[8]采集到的北京市出租车地理位置信息数据的散点图,横坐标为经度,纵坐标为纬度.
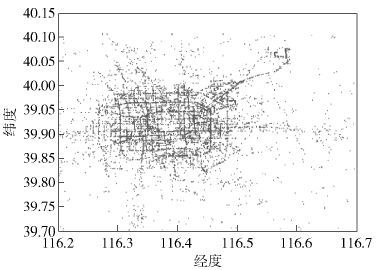
|
图 2 出租车地理位置散点图 |
把此散点图二值化,DBSCAN中定义的孤立点在散点图中表现为噪声.
数据空间定义:S=D1×D2,其中D1为经度,D2为维度,数据空间中的点集合定义为
P={P1,P2,…,Pn},Pi=(I,di1,di2),i∈{1,2,…,n}
其中:I为点的唯一编号,di1为点的经度,di2为点的维度.
数据划分:在本算法中,每一维都采用相同的单位值进行划分.
单元格:对数据空间的每一维都进行等长划分,长度为l=f(E)(f称为伸缩函数),整个空间被划分为有限个网格G={Gm,n},0 <m,0<n,每个单元格都是一个正方形,用二元组表示为Gm,n=(N,List〈I〉).
对于数据空间中的所有点,计算其所属的单元格:
Pi Gx,y,if(di1/l>x and di1/l≤x+1and di2/l>y and di2/l≤y+1)
其中x、y分别为单元格在空间中的坐标.
相邻单元格:如果两个单元格具有相同的边,则称为近邻单元格;若相同顶点,则称它们为远邻单元格. 在这样的定义下,划分后的数据空间中,除了边界单元格以外,每个单元格都有8个邻居,其中4个为近邻,4个为远邻.
单元格密度:单元格中包含的数据点数量为Dx,y=|Gx,y|.
核心点:邻域范围E内邻居数量不少于M的数据点.
边界点:邻域范围E内邻居数量小于M,但是其邻居中存在核心点的数据点.
噪声点:邻域范围E内邻居数量小于M,并且其邻居都不是核心点的数据点.
根据上述定义,对数据集合中的点进行计算,放入划分的单元格中. 当所有点处理完毕后,可以得到每个单元格的密度. 如果取
模板矩阵:
聚合运算:定义运算⊗,则
| $M\otimes {{G}_{i,j}}=\left\{ \begin{matrix} \underset{m=i-1,n=j-1}{\overset{i+1,j+1}{\mathop{\sum }}}\,{{m}_{m,n}}|{{D}_{m,n}}|,if\underset{m=i-1,n=j-1}{\overset{i+1,j+1}{\mathop{\sum }}}\,|{{D}_{m,n}}|>M \\ -\underset{m=i-1,n=j-1}{\overset{i+1,j+1}{\mathop{\sum }}}\,|{{D}_{m,n}}|,其他 \\ \end{matrix} \right.$ |
运算的结果是计算单元格及其邻居单元格中一共包含多少个数据点.
在所设计的算法中,有两个重要因素:第一是空间划分的粒度;第二是模板矩阵的取值. 在实际运行中,将划分粒度设置为0.5E,这样,一个单元格以内的数据点一定会为E邻居. 划分后,单元格与E的关系如图 3所示.
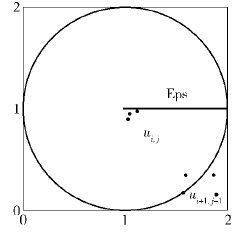
|
图 3 单元格划分示意图 |
在图 3中可以看出,如果单元格ui,j中的数据点位于左上角,则单元格ui+1,j-1中的数据点不全部在u的邻居范围内,此时模板矩阵中对应的元素应该取小于1的数值.
2 算法描述基于上述的描述,给出如下算法.
算法1
输入:数据点P,M,E
输出:Clusters
1. Get Max(x),Max(y),Min(x),Min(y)
2. Initialize matrix templates M1,M2,M3,M4
3. l≤f(E)
4. Calculate the volumes of X and Y
5.
6. Initialize Array G of grids with size X*Y
7. Initialize List Clusters ={Cluster_Res,Cluster_Noise}
8. Foreach p in P
9. x=L(p.x-Min(x))/l」,y=L(p.y- Min(y))/l」
10. G[x,y].PointIds.add(p.ID)
11. G[x,y].Centroid.x= (G[x,y].Centroid.x *G[x,y].PointNumber+p.x)/ G[x,y].PointNumber+1
12. G[x,y].Centroid.y= (G[x,y].Centroid.y *G[x,y].PointNumber+p.y)/ G[x,y].PointNumber+1
13. G[x,y].PointNumber++
14. End Foreach
15. For i=1 to Y-1
16. For j=1 to X-1
17. If G[i,j].PointNumbers!=0 then
18. Selecting matrix template Mi according to G[i,j].centroid
19.G[i,j].PointNumbers=Mi⊗G[i,j]
20.If G[i,j].PointNumbers>M
21. Cluster_Res.add(G[i,j].PointIDs)
22. For m=i-1 to i+1
23. For n=j-1 to j+1
24. If(G[m,n].PointNumbers <0)
25. G[m,n].PointNumbers=-G[m,n].PointNumbers
26. Cluster_Res.add(G[m,n].PointIDs)
27. Cluster_Noise.remove(G[m,n].PointIDs)
28. Endif
29. Endfor
30. Endfor
31. Else
32. G[i,j].PointNumbers=- G[i,j].PointNumbers
33. Cluster_Noise.add(G[i,j].PointIDs)
34. Endif
35. Endif
36. Endfor
37. Endfor
算法的开始首先计算空间的大小,并根据E确定空间划分的粒度. 在所提的算法中,每一维上的粒度是相同的,都是E的函数.
空间的大小比实际的数据范围增加了两行两列,如第5行所示,这是为了计算方便的需要. 如果按照实际的数据空间大小划分,则需要对边界单元格单独处理,因为这些单元格的邻居数目小于8,在进行⊗运算时需要增加额外的计算量.
第7行创建两个集合,分别保存聚类后的簇内元素和噪声点. 第8~14行完成单元格的划分.
数据聚类的过程在第15~37行完成. 聚合运算⊗的作用在于判断一个单元格内部的数据点是否有多于M个邻居,⊗运算相当于累加一个单元格与其邻居包含的数据点总数. 若运算结果C大于M,说明该单元格内的数据点都是核心点,则用C替换该单元格的N属性值;否则,将单元格的N属性值设为-N. 这样做的目的在于,如果该单元格内的数据点邻居数小于M,则这些点有两种可能:噪声点或者边界点,还有待于进一步判断.
3 算法分析与评估所提算法在运算过程中只需要判断一个单元格及其邻居单元格中数据点的数量,不需要计算距离,因此算法时间复杂度为O(c,m ). 其中,m为单元格个数,其值取决于划分单元格所采取的粒度,m与n无关;c为常数,其大小与模板矩阵有关.
为了验证算法的效果和性能,对算法进行了实验评估,并与DBSCAN、CLIQUE进行了对比. 算法实现语言为Java,运行环境为8 GB内存、I7双核处理器、64位Windows7操作系统.
测试数据为微软亚洲研究院的Geolife项目采集的GPS轨迹数据GEO. 为了简化实验过程,首先在数据集中按照经纬度坐标从小到大取前1万个数据,得到的数据散点图如图 4(a)所示.
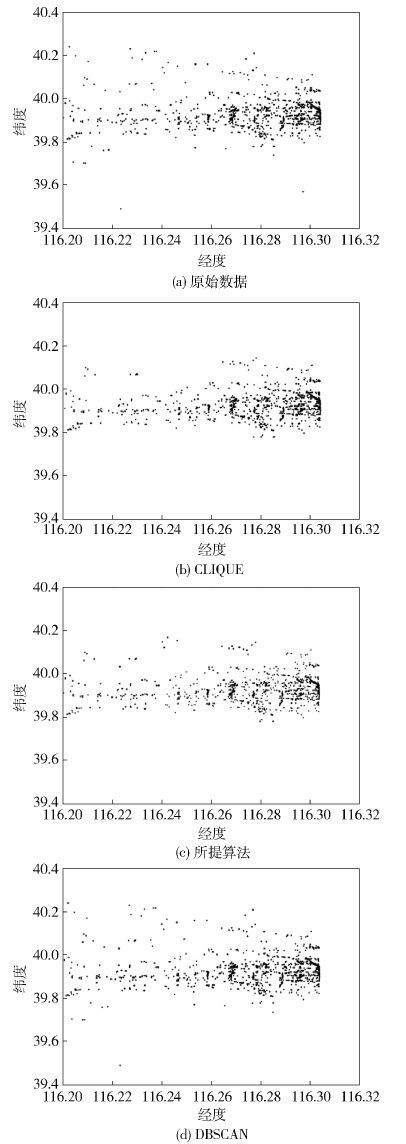
|
图 4 聚类结果对比 |
然后,以此数据集为输入,分别运行DBSCAN算法、CLIQUE算法和所提算法对数据进行聚类. 在DBSCAN算法中,E的取值为0.02,M的取值为4;在CLIQUE算法中,二维空间共划分为150×150个矩形,即ε=150,密度阈值ω=4;在所提算法中,M的取值为4,单元格的长度为0.01. 算法运行后效果如图 4所示.
通过图 4可以直观看到,DBSCAN算法结果中数据点多于所提算法结果,如图 4(d)左上部所提算法据点;所提算法结果数据点多于CLIQUE算法,如图 4(c)中上部DBSCAN数据点. 因此可知所提算法的精度低于DBSCAN但是高于CLIQUE.
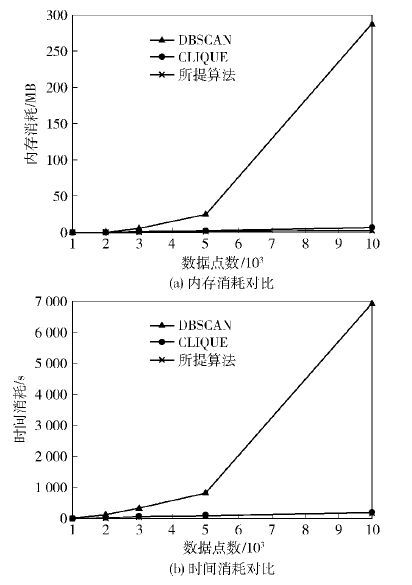
单纯的直观观察难以分析算法的性能,接下来进行多次实验,在效率、性能和精度等方面进行定量分析. 分别取数据集大小为1 000、2 000、3 000、5 000和1万个数据,依次使用3种算法进行聚类,记录各种算法在内存消耗、运行时间和精确度方面的数据. 其中,不同算法的内存消耗和CPU时间消耗对比如图 5所示.
|
图 5 DBSCAN、CLIQUE和所提算法效率对比 |
由图 5可以看出,无论在内存消耗还是CPU时间消耗上,所提算法都优于DBSCAN;和CLIQUE算法相比,所提算法在运行时间上优于CLIQUE算法,但在内存消耗上略占劣势,这是因为在划分单元格时,所提算法在两个维度上是根据经纬度换算后采用同样长度的距离划分的,在数据集中,经度跨距大于纬度跨距,因此,在X和Y
实验方法:取数据集中的全部数据点,分别运行DBSCAN、CLIQUE和所提算法. 每一轮都改变输入参数,分别记录各种算法运行结果中聚类精度. 聚类精度包括形成聚类的个数和误判数据点数. 所谓误判数据点是那些本来数据聚类内部点(核心点或者边界点)但是被算法判别为噪声的点. 实验结果如表 1所示.
|
|
表 1 算法精度对比 |
通过表 1可以看出,在空间划分粒度较小的情况下,CLIQUE产生的聚类数目精度较低,所提算法接近于实际值. 当空间划分粒度增大时,CLIQUE和所提算法在误判噪声点方面精度都会有一定程度的降低,这是因为单元格较大时,包含边界点的单元格数目与总单元格数的比例会增加,CLIQUE算法会将这些单元格内的数据点作为噪声,而所提算法在处理这类单元格时参考了其邻居单元格的性质,因此提高了精度,误判噪声点的比例大大降低,无论在聚类个数还是误判噪声点方面,所提算法都比CLIQUE具有更高的精度.
4 结束语针对海量数据流提出了一种网格划分与密度相结合的聚类算法,重点关注数据集中的噪声数据. 通过矩阵模板过滤掉噪声数据点,通过判断邻居属性来识别边界数据点. 这样的方法相比完全基于密度的DBSCAN算法,大大提高了运行效率;相对于完全基于网格的CLIQUE算法,则能够获得更高的聚类精度.
所提出的算法另外很重要的一点是,该算法很容易在分布式环境下进行实现. 在具体实验过程中,将划分网格后的结果矩阵再次分为多个上下边界重叠的子矩阵,使用多个线程分别运算,最后再对各线程的处理结果进行合并. 这种运算模式符合MapReduce的特征,下一步的工作是研究算法的并行化,在MapReduce平台上进行实验验证.
| [1] |
Han Jiawei, Micheline Kamber, Pei Jian.
Data mining:concepts and techniques[M]. Burlington, Massachusetts: Morgan Kaufmann , 2011 : 444 -476.
( 0) 0)
|
| [2] |
Martin Ester, Hans-Peter Kriegel, Jorg Sander, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of KDD. Portland, USA:AAAI Press, 1996:226-231.
( 0) 0)
|
| [3] |
Ankerst M, Breunig M, Kriegel H P. OPTICS:ordering points to identify the clustering structure[C]//Acm Sigmod Record. New York, NY, USA:Philadelphia, PA, 1999:49-60.
( 0) 0)
|
| [4] |
Hinneburg A, Keim D A. An efficient approach to clustering in large multimedia databases with Noise[C]//Proceedings of the International Conference on Knowledge Discovery and Data Mining (KDD'98). 1998:58-65.
( 0) 0)
|
| [5] |
Wang Wei, Yang Jiong, Muntz R. STING:A statistical information grid approach to spatial data mining[C]//Proceedings of the 23rd International Conference on Very Large Data Bases. San Francisco, CA. USA:Morgan Kaufmann Publishers Inc:1997:186-195.
( 0) 0)
|
| [6] |
Agrawal R, Gehrke J, Gunopulos D, et al. Automatic subspace clustering of high dimensional data for data mining application[C]//Proceedings of the 1998 ACM SIGMOD International Conference on Management of Data. ACM:New York, NY, USA. 1998:94-105.
( 0) 0)
|
| [7] |
Sheikholeslami G, Chatterjee S, Zhang Aidong. WaveCluster:a multi-resolution clustering approach for very large spatial databases[C]//Proceedings of the 24th VLDB Conference. Morgan Kaufmann:New York, USA. 1998:428-439.
( 0) 0)
|
| [8] |
Zheng Yu, Xie Xing, Ma Weiying. GeoLife:A collaborative social networking service among User, location and trajectory[J]. IEEE Data Engineering Bulletin , 2010, 33 (2) :32–40.
( 0) 0)
|


