针对无线传感网中能源高效的实时数据收集问题,提出了包含节点聚簇、路径规划、合并路径和数据收集4个阶段的移动数据收集协议和节省开销及近邻2个启发式路径规划算法,构建了满足时延且移动开销最小的数据收集路径.仿真结果表明,提出的路径规划算法在节约网络能耗、保证时延要求和减少移动开销等方面都更具优势.
The energy efficient and real-time data collecting problem in wireless sensor network was studied. The mobile data collecting protocol consists four phases:nodes clustering, routes planning, routes combine and data collecting is proposed. Two heuristic algorithms save and nearest neighbor were presented to build data collecting routes which incur the least mobile cost while satisfy the deadline constraint. Simulations show that the proposed heuristic routes planning algorithms have good performance in terms of energy saving, deadline guarantee and travel cost reduction.
在无线传感网中,利用车载或手持智能节点作为移动数据收集器(MDC,mobile data collector)收集数据,能有效地减少无线传输能耗,延长网络寿命[1]. Yao等[2]提出能耗均衡的移动数据收集协议. 基于集合点的数据收集(RDC,rendezvous data collection)协议[3]通过遍历路由树选择汇聚节点. 基于连通的数据收集(CBDC,connectivity-based data collection)协议[4]根据节点连通性划分聚簇,调整单跳和多跳节点比例,在节能和时延之间权衡. Liang等[5]将距离受限的移动路线规划问题用线性混合整数规划模型求解. Tashtarian等[6]利用决策树和动态规划方法确定游走路线. 笔者提出一个4阶段的移动数据收集协议(MDCP,mobile data collecting protocol),包括节点聚簇、路径规划、合并路径和数据收集. 由于带时间约束的路径规划问题是非确定性多项式(NP,non-deterministic polynomial)难的,提出节省开销(SAV,save)和近邻(NN,nearest neighbor)2个启发式算法,构建满足时延且移动开销最小的游走路径. 仿真结果表明,算法的节能、时延和移动开销效果优于现有算法.
1 移动数据收集协议MDCP移动数据收集协议MDCP包含4个阶段.
阶段1 节点聚簇. 初始时传感器节点随机一致部署在监控区域,笔者使用与CBDC协议[4]相同的聚簇方法将节点分为M个聚簇{CP1,CP2,…,CPM},所有簇成员节点将数据汇集到簇头,由MDC主动收集.
阶段2 路径规划. 构建最小移动开销且满足时延的路径集合,每条路径派发一个MDC.
阶段3 路径合并. 路径合并源于成本预算对MDC个数的限制. 为避免路径合并后违反时延要求,用贪心方法选择路径长度减少最多、无线多跳传输能耗增加最少的聚簇合并,减少路径长度.
阶段4 数据收集. MDC从基站出发,访问路径上的所有簇头,最后携带数据返回基站.
2 路径规划 2.1 问题描述笔者重点研究MDCP协议中的路径规划算法. 首先给出如下定义和变量说明,如表 1所示.
|
|
表 1 符号变量说明 |
定义1 无向图G
无向图G=(V,E),其中V={0,1,…,n}为簇头集合,E⊆V×V,E={(i,j)|i,j∈V}为边的集合.
定义2 路径P
在无向图G=(V,E)中,路径P为簇头的序列P=(i1,i2,…,ik),路径上相邻节点之间有边,即(ij,ij+1)∈E,1≤j≤k-1.
路径规划问题的形式化定义为
| ${{S}^{*}}=arg\text{ }minC\left( S \right)$ | (1) |
其中:S
| $C({{R}_{i}})={{c}_{0,{{i}_{1}}}}+\underset{j=2}{\overset{k}{\mathop{\sum }}}\,{{c}_{{{i}_{j-1}},{{i}_{j}}}}+{{c}_{{{i}_{k}},0}}$ | (2) |
上述问题可归约为带时间约束的多旅行商问题,属于NP难问题. 笔者提出2个启发式算法.
2.2 SAV启发式算法1) 基本思想. 初始时并行地为每个簇头构建一条直接到达基站的路径,然后选择代价节省最多的路径合并,合并路径时考虑路径的时间约束,直到没有可合并的路径时,算法终止. 合并路径节省的代价为
| ${{a}_{ij}}={{d}_{oi}}+{{d}_{oj}}-{{d}_{ij}},1\le i,j\le n,i\ne j$ | (3) |
其中:doi为从基站直达节点i再返回基站的距离;dij为从基站到节点i再到节点j,最后从j返回基站的距离.
2) 兼容路径. 如果节点i为某路径的终止节点,节点j为另一条路径的起始节点,或相反,则称这2条路径兼容.
3) 时延检验. 设路径Ri=(i0,i1,…,ip-1,ip,…,im),若在ip-1和ip间插入节点x,路径扩大为Ri=(i0,i1,…,ip-1,x,ip,…,im).
| ${{b}_{{{i}_{p}}}}={{b}_{{{i}_{p-1}}}}+{{s}_{x}}$ | (4) |
| ${{b}^{new}}_{{{i}_{p}}}={{b}_{{{i}_{x}}}}+{{s}_{x}}$ | (5) |
插入新节点x后节点ip的访问时间变化为
| ${{\Delta }_{{{i}_{p}}}}={{b}^{new}}_{{{i}_{p}}}-{{b}_{{{i}_{p}}}}$ | (6) |
如果Δip >0,则新路径中节点ip之后的某些节点就可能不满足时延要求,因此需要时延检验. 以向前推进的方式依次检验ip之后每个节点的时延.
算法1 基于代价的启发式算法SAV
输入 1)网络无向图G; 2)路径时延限制L
输出 优化的路径集合S
1初始化路径集合S={R1,R2,…,Rn}
2 for i=1 to n do
3 for j=1 to n do
4 根据式(3)计算aij
5 创建aij的大根堆H
6 repeat
7取H的根aij
8 if Rki和Rjm为兼容路径 then
9 合并Rki和Rjm为新路径Rkm
10 if Rkm通过时延检验 then
11 删除Rki和Rjm
12 插入Rkm到集合S
13 取H的下一个aij
14 goto 第8行
15 until H为空或再无可合并的路径
16 返回集合S
2.3 NN启发式算法1) 基本思想. 首先选择距离基站最近的节点加入路径,在后续的扩大路径过程中,每次总是选择距离上一个新加入节点最近的节点加入路径. 如果路径的长度超过了时间约束的路径长度,则构建一条新的从基站出发的路径,当网络中所有节点都加入到路径集合中时,算法结束.
2) 近邻的度量. 基于近邻的启发式算法不仅考虑节点之间的位置邻近,还考虑节点之间的时间邻近. 近邻度为
| ${{c}_{ij}}={{\beta }_{1}}{{d}_{ij}}+{{\beta }_{2}}{{T}_{ij}}+{{\beta }_{3}}{{u}_{ij}},\text{ }\underset{i=1}{\overset{3}{\mathop{\sum }}}\,{{\beta }_{i}}=1,{{\beta }_{i}}\ge 0$ | (7) |
| ${{b}_{j}}=max~\{{{e}_{j}},{{b}_{i}}+{{s}_{i}}+{{t}_{ij}}\}$ | (8) |
| ${{T}_{ij}}={{b}_{j}}-({{b}_{i}}+{{s}_{i}})$ | (9) |
| ${{u}_{ij}}={{l}_{j}}-({{b}_{i}}+{{s}_{i}}+{{t}_{ij}})$ | (10) |
其中:cij为节点i和j的邻近度,dij为欧式距离,Tij为访问时间的差异,uij为从i到j的时间紧迫度.
算法2 基于近邻的启发式算法NN
输入 1)网络无向图G=(V,E); 2)路径时延L
输出 优化的路径集合S
1 初始化 S=∅,k=0,V'=V
2 for V′中每个节点i do
3 根据式(9)计算i到基站的近邻度量值c0i
4 repeat
5 选择最小近邻值节点加入路径Rk=(0,i)
6 更新节点集合V′=V′-{i}
7 for V′中每个节点j do
8 计算节点j到路径Rk中最后节点i的cij
9 选择最小近邻值节点加入路径Rk=(0,i,j)
10 if L(Rk) <L then
11 扩大子路径Rk=(0,i,j)
12 else
13 S=S∪Rk,k=k+1
14 goto 第5行 构建一个新路径
15 until V′集合空
16 返回集合S
3 仿真结果 3.1 实验设置实验采用NS-2仿真,模拟1000个节点随机均匀分布在800m×800m的网络中. 控制MDC移动速度在[0.2m/s,2m/s]区间. 只考虑发送和接收数据的能耗. 实验考察4个不同数据收集算法的能耗和移动开销. SAV和NN为笔者提出的启发式路径规划算法,和RDC协议[6]和CBDC协议[7]进行对比.
3.2 节点数量对性能的影响图 1表明,时延越长,能耗越低,因为MDC可主动收集更多的簇头节点数据;节点数量增加,导致网络能耗线性增加,这是因为聚簇内节点数量增加,导致无线传输增加.
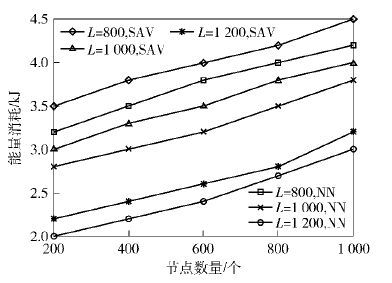
|
图 1 路径约束和节点数量对启发式算法能耗的影响 |
图 2表明,SAV和NN的传输能耗低于RDC和CBDC,这是因为RDC和CBDC协议簇内成员节点采用多跳路由方式将数据汇聚到簇头,而SAV和NN采用一跳传输机制.
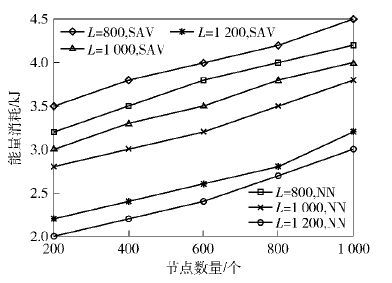
|
图 2 节点数量对4种数据收集算法能耗的影响 |
图 3表明,在节点数量增加时,所有协议的移动开销都增加,因为MDC需要用更长或更多的游走路径收集全网的数据. 相比之下,SAV和NN的移动开销低于RDC和CBDC,因为启发式算法以最小化移动开销为优化目标.
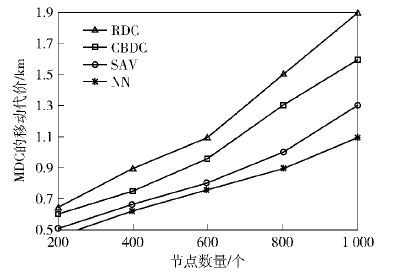
|
图 3 节点数量对移动开销的影响 |
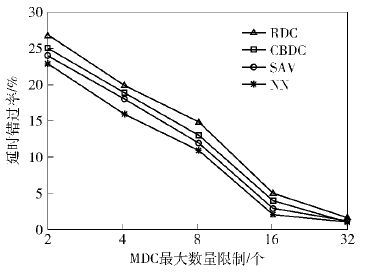
图 4表明,增加MDC的数量,可增多并发数据收集的路径,因此无线多跳传输能耗减少. 图 5表明,MDC的最大个数增加,时延错过率显著下降. 笔者所提算法采用了路径合并技术,时延错过率低于RDC和CBDC. NN算法考虑了时延和剩余时间,比SAV算法时延错过率低.
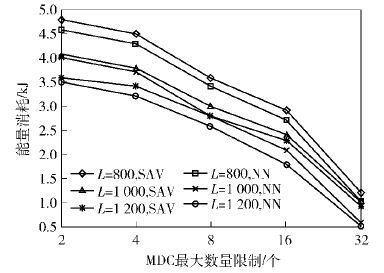
|
图 4 MDC的最大数量对能耗的影响 |
|
图 5 MDC的最大数量对时延错过率的影响 |
移动sink主动收集数据替代传统的无线多跳路由可节省大量的网络能耗. 笔者提出了4阶段移动数据收集协议MDCP,重点研究了路径规划阶段的优化问题,提出了基于代价的启发式算法SAV和基于近邻的启发式算法NN. 实验结果表明,使用笔者所提路径规划算法的移动数据收集协议,在节能、时延保证和移动开销等方面都优于现有协议.
| [1] |
Mario D F, Sajal K. Data collection in wireless sensor networks with mobile elements:a survey[J]. ACM Transactions on Sensor Networks , 2011, 8 (1) :1–31.
( 0) 0)
|
| [2] |
Yao Xuan, Huang Hongyu, Tang Jiqiang, et al. Residual energy aware mobile data gathering in wireless sensor networks[J]. Springer Telecommunication Systems , 2014, 58 (4) :1–11.
( 0) 0)
|
| [3] |
Xing Guoliang, Wang Tian, Jia Weijia, et al. Rendezvous design algorithm for wireless sensor networks with mobile base station[C]//Proc of the ACM MobiHoc. New York:ACM Press, 2008:231-240.
( 0) 0)
|
| [4] |
Abdullah I A, Khaled D M, Haitham A A, et al. Connectivity-based data gathering with path-constrained mobile sink in wireless sensor networks[J]. Wireless Sensor Network , 2014 (6) :118–128.
( 0) 0)
|
| [5] |
Liang Weifa, Luo Jun, Xu Xu. Prolonging network lifetime via a controlled mobile sink in wireless sensor networks[C]//Proc of the IEEE GlobeCom. New York:IEEE Press, 2010:1-6.
( 0) 0)
|
| [6] |
Tashtarian F, Moghaddam M H Y, Sohraby K, et al. ODT:optimal deadline-based trajectory for mobile sinks in WSN:a decision tree and dynamic programming approach[J]. Computer Network , 2015, 7 (11) :128–143.
( 0) 0)
|


