2. 哈尔滨工业大学(威海) 计算机科学与技术学院, 山东 威海 264209
为解决无线传感器网络中继节点设置位置不合理而导致的网络构建成本高、网络整体寿命低等问题,提出了一种基于贪婪准则的中继节点布局算法.该算法采用能耗均衡率和网络总能耗等性能评价标准,分别对最近贪婪准则、定向贪婪准则和角度最小贪婪准则进行了多角度的对比分析,并引入数据流向限制、通信容量和数据最大转送次数,对节点数据传输路径进行约束及优化.实验结果表明,最近贪婪准则能耗少,网络中各个节点的能耗均衡,可给出合理的中继节点布设位置,有效降低网络的整体能耗.
2. School of Information and Electrical Engineering, Harbin Institute of Technology at Weihai, Shandong Weihai 264209, China
In order to solve the problem of high cost of network construction and low lifetime of network, it is a problem to solve the problem of high cost of network construction and low network lifetime of relay nodes in wireless sensor network,this article proposed a new relay node placement algorithm based on the greedy criterion. By adopting the performance evaluation criteria of the balanced energy consumption rate and the total energy consumption of the network, the algorithm contrasts the recent greedy criterion, the directional greedy criterion and the minimum angle of greedy criterion respectively, and then constrains and optimizes the data transmission path of node by introducing data flow restriction, communication capacity and maximum data transfer times. Experiments show that, the recent greedy criterion has less energy consumption, and can balance the energy consumption of each node in the network. Moreover, this recent greedy criterion can not only give proper location of each node, but also reduce the energy consumption of the whole network effectively.
无线传感器网络(WSN,wireless sensor networks)通常由传感器节点(SN,sensor node)、中继节点(RN,relay node)、汇聚节点(SINK,sink node)组成[1]. 对于单层传感器网络,Lin等[2]提出了最小生成树的5-近似算法. Tang等[3]研究了大范围网络节点的布局问题. Cheng等[4]研究了如何布设最少的中继节点来保证网络的连通性. 刘洲洲等[5]针对节点能量有限的问题,提出了一种能量有效的无线传感器网络无标度拓扑模型.
可见,目前对于中继节点布局算法的研究并没有综合考虑RN数目与能耗之间的关系. 笔者在前期工作[6]的基础上,进一步对多种贪婪准则在RN设置算法的应用进行综合对比分析,寻找最优算法,保证网络节点间能耗均衡的基础上进一步降低网络整体能耗,延长网络寿命.
1 问题描述 1.1 网格间距实际应用中,WSN的RN的布设位置可能会受到诸多物理因素限制,导致它们不能布设在监测区域的任意位置. 为适应复杂地理环境的特点,设计了基于网格结构的中继节点布局算法. 首先要合理设定网格的大小,笔者在课题组研究的基础上,网格间距依据文献[7]选取,其选取原则为
| $L\le R/\sqrt{10}$ | (1) |
其中:L为网格间距;R为节点通信半径.
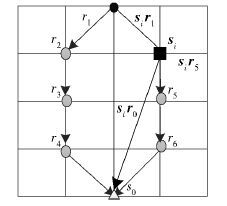
1.2 约束条件 1.2.1 数据流向限制在SN选择路径时,如果不限制数据流向,SN将任意选择节点转送数据,可能导致数据流向与SINK节点所在方向相反,增加网络能耗. 设存在节点si,该节点将数据转送到节点s0的路径如图 1所示.
|
图 1 RN节点路径选择 |
在图 1中,节点si到节点s0的方向向量为sis0,并称此向量为基准向量. 设RN节点集RN={ri,…,rn},根据数据流向,节点间向量可表示为sirj、rjrm和rms0. 设Re_1、Re_2和Re_3表示形式为
| ${{R}_{e\_1}}={{s}_{i}}{{s}_{0}}{{s}_{i}}{{r}_{j}}$ | (2) |
| ${{R}_{e\_2}}={{r}_{j}}{{r}_{m}}{{s}_{i}}{{s}_{0}}$ | (3) |
| ${{R}_{e\_3}}={{r}_{m}}{{s}_{0}}{{s}_{i}}{{s}_{0}}$ | (4) |
为了限制RN数目,除了SINK节点以外,其他节点间组成的向量与sis0之间的向量角不应大于90°,因此应保证Re_1、Re_2和Re_3的值大于0.
1.2.2 通信容量设置通信容量是指节点可转送最大数据的能力. SN与RN在选择下一跳节点的过程中,RN要衡量其最大的通信容量,只有通信容量在节点的承受范围之内,才有能力转送数据,如果通信容量超过限制,则选择其他的RN继续通信. 当寻找到符合通信容量的节点时,数据信息可正常转送.
1.2.3 数据最大转送次数为降低网络的整体能耗,避免在多跳网络中出现逐跳转送数据的现象,提出了限制数据最大转送次数的问题. 所谓数据最大转送次数,即SN将数据转送到SINK节点的路径中,RN的数目不能超过一个定值. 由图 1可知,通过式(5)限定SN到SINK节点数据转送的最大跳数Jump_max (si,s0),使数据尽可能沿sis0方向传输至SINK节点,可减少需要布设的RN数目.
| $Jump\_max~({{s}_{i}},{{s}_{0}})=\left\lceil \frac{d({{s}_{i}},{{s}_{0}})}{L} \right\rceil $ | (5) |
其中d(si,s0)为SN与SINK的节点间距.
1.3 算法性能评价标准 1.3.1 能耗均衡率一个完善的中继节点布局算法不仅要保证网络整体能量消耗小,还要保证网络整体能耗分布均衡,能耗均衡率与网络的生命周期成正比,即均衡率越高,网络生命周期就会越长[8]. 设节点si主路径的能耗为energy_consunmi1,辅路径能耗为energy_consunmi2,则节点si路径组总能耗为
| $E{{C}_{i}}=energy\_consun{{m}_{i1}}+energy\_consun{{m}_{i2}}$ | (6) |
节点si路径组总能耗的最大值、最小值为
| $E{{C}_{max~}}=max~\{E{{C}_{i}}\}$ | (7) |
| $E{{C}_{min~}}=min~\{E{{C}_{i}}\}$ | (8) |
网络中n个SN的总能耗TEC为
| ${{T}_{EC}}=\sum\limits_{1}^{n}{E{{C}_{i}}}$ | (9) |
能耗均衡率p的求取为
| $p=1-E{{C}_{max~}}-E{{C}_{min~}}{{T}_{EC}}$ | (10) |
由式(10)可知,能耗均衡率p更加直观地反映了不同路径之间能耗的离散程度,且能耗均衡率的值小于等于1. 由此可知,耗能均衡率的问题可看作组合优化问题.
1.3.2 RN数目与网络总能耗评估算法在延长网络生命周期方面的有效性时,除了要分析网络的能耗均衡率,同时也要对网络RN数目、网络总能耗等方面进行分析. 合理的分析将有助于提高网络资源的利用率,使网络在较低的成本下,尽可能延长生命周期. 因此,在保证网络能耗分布均衡的基础上,通过算法减少网络布设的RN数目、降低网络总能耗、提高网络生命周期和保证网络的稳定性至关重要.
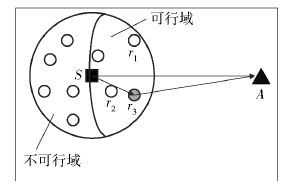
1.4 贪婪准则描述贪婪算法涉及的3种贪婪准则分别为最近贪婪准则(NGC,nearest greedy criterion)、定向贪婪准则(DGC,directional greedy criterion)和角度最小贪婪准则(ALGC,angle least greedy criterion),原理如图 2所示.
|
图 2 贪婪准则原理 |
由图 3可知,在贪婪准则中,源节点S的转送数据区域根据数据流向限制机制,被分为2个区域. 邻居节点到目的节点A的距离不大于源节点S到目的节点A的距离的区域叫作可行域,可行域内的节点集为
| $RN\_range\_feasible=\{{{r}_{i}},\ldots ,{{r}_{j}}\}$ | (11) |
针对网络容错能力有限问题,提出了基于贪婪准则的容错性路径组算法,该算法为每个传感器节点选择2条路径,即主辅路径,当主路径产生故障时,即启用辅路径. 主辅路径配合提高网络的容错性. 3种贪婪准则容错性中继节点布局算法步骤如下.
输入 监测区域坐标(a,b)、SINK节点坐标(x0,y0)、网格间距L、SN个数n、SN位置坐标、SINK节点s0、通信容量k、通信半径R和准则选择因子α(α的定义为:α=1,代表选择NGC算法;α=2,代表选择DGC算法;α=3,代表选择ALGC算法).
输出 RN坐标、WSN能耗等.
步骤1 根据通信半径等信息确定网格间距,并将监测区域网格化,所有的网格交点坐标都是RN节点的候选位置坐标,记为RN={r1,r2,…,rm}.
步骤2 统计每个节点si到节点s0之间的距离d(si,s0),将该距离按照由大到小排列为d={d1,d2,…,dn},其中每个节点si都对应一个距离参数di. SN数据信息转发最大跳数为Jump_max (si,s0).
步骤3 判断是否di≤R,如果成立,di对应的sd直接与s0通信,并在d中删除di值.
步骤4 判断α值,转到与其对应的算法入口处.
步骤5 从最大距离d1对应的节点si开始,在可行域节点RN_range_feasible={ri,…,rj}内,选择符合条件的下一跳节点rj,更新Jump_max (si,s0)值为Jump_max (si,s0)-1.
步骤6 rj在其可行域内搜索符合条件的节点,其具体步骤如下.
如果rj的通信容量满足算法设计要求,在rj的可行域内搜索符合条件的sj,若有节点sj符合要求,则把rj选为sj的下一跳节点,同时删除sj在d中对应的距离值.
如果rj的通信容量超过限制或可行域内无符合条件的SN节点,则
步骤7 rh按照步骤6重复操作,同时更新rh的通信容量值,更新后的结果为rh的通信容量与rj传递数据信息容量之差.
步骤8 待一条路径选择完毕后,重复步骤5与步骤6.
步骤9 如果d为空集,RN内删掉候选RN的集合,从步骤2开始为SN选择辅路径. 这种布设路径的方式保证了主辅2条路径的必然存在性. 一直到d再次为空集,算法执行完毕.
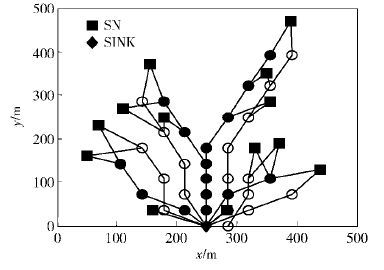
3 性能评估仿真环境的监测区域设置为500 m×500 m,通信半径R为100 m,网格间距为36 m,SN发送数据k=12 bit,RN通信容量设为37 bit. 随机分布13个SN,则3种贪婪准则实验结果如图 3、图 4和图 5所示. 图中SN为传感器节点的预设位置,SINK节点为网关节点的位置,圆点为根据算法布设的最优中继节点的位置.
|
图 3 NGC容错性路径组仿真图 |

|
图 4 DGC容错性路径组仿真图 |
|
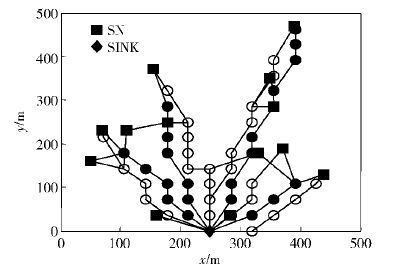
图 5 ALGC容错性路径组仿真图 |
NGC、DGC和ALGC的容错性路径组的RN数目分别为32、45和47,其他算法性能分析结果如表 1所示.
|
|
表 1 3种贪婪准则路径组对比 |
NGC容错性路径组算法和其他算法相比,无论网络总能耗还是能耗均衡率等方面,都占有明显优势. 同时,对不同数目的SN进行了大量实验,从多个角度对算法进行评价,如图 6所示.
|
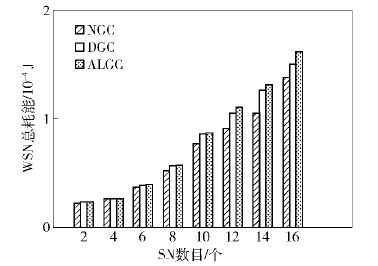
图 6 WSN总能耗对比 |
由图 6分析得,在容错性路径组算法应用过程中,3种算法总能耗方面差距不明显,但是随着SN数目的逐步增加,NGC容错性路径组算法应用最少数目的RN节点,其网络总能耗也最少,对算法的能耗均衡率进行了对比分析,如图 7所示.
|
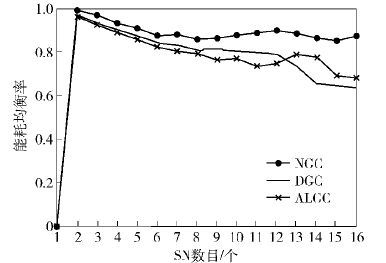
图 7 能耗均衡率对比 |
从图 7可以看出,随着SN数目的增加,NGC容错性路径组算法能量分布一直比较均衡,其他2种算法能量均衡率变化波动比较明显,由此得出,NGC容错性路径组算法的性能较高,达到了降低网络能耗、均衡网络能耗、延长网络生命周期的目的.
4 结束语研究了基于3种贪婪准则的中继节点布局,旨在解决WSN节点能量有限导致网络生命周期短的问题. 在算法设计过程中,引入约束条件对中继节点的路径选择进行约束和优化,并提出了能耗均衡率、RN数目和网络整体能耗等性能评价标准. 大量实验验证表明,最近贪婪准则能有效均衡WSN节点间能耗,降低网络整体能耗,达到延长网络寿命的目的. 在今后的实际应用工作中,可优先采用这种算法进行WSN节点布设.
| [1] |
钱志鸿, 王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报 , 2013, 35 (1)
:215–227.
Qian Zhihong, Wang Yijun. Internet of things-oriented wireless sensor networks review[J]. Journal of Electronics and Information Technology , 2013, 35 (1) :215–227.
( 0) 0)
|
| [2] |
Lin G H, Xue G L. Steiner tree problem with minimum number of steiner points and bounded edge-length[J]. Information Processing Letters , 1999, 69 :53–57.
doi:10.1016/S0020-0190(98)00201-4 ( 0) 0)
|
| [3] |
Tang Jian, Hao Bin, Sen Arunabha. Relay node placement in large scale wireless sensor networks[J]. Computer Communications , 2006, 29 (4) :490–501.
doi:10.1016/j.comcom.2004.12.032 ( 0) 0)
|
| [4] |
Cheng Xiuzhen, Du Dingzhu, Wang Lusheng, et al. Relay sensor placement in wireless sensor networks[J]. Wireless Networks , 2007, 14 (3) :347–355.
( 0) 0)
|
| [5] |
刘洲洲, 王福豹. 能量有效的无线传感器网络无标度拓扑模型[J]. 北京邮电大学学报 , 2012, 38 (1)
:87–91.
Liu Zhouzhou, Wang Fubao. Scale-free topology for wireless sensor networks with energy efficient characteristics[J]. Beijing University of Posts and Telecommunications , 2012, 38 (1) :87–91.
( 0) 0)
|
| [6] |
王翥, 王祁, 魏德宝, 等. 无线传感器网络中继节点布局算法的研究[J]. 物理学报 , 2012, 61 (12)
:120505–1.
Wang Zhu, Wang Qi, Wei Debao, et al. Relay node placement and addition algorithms in wireless sensor networks[J]. Acta Phys Sin , 2012, 61 (12) :120505–1.
( 0) 0)
|
| [7] |
Wang Z, Lv C, Shao X. An improved relay node layout approach in wireless sensor networks[J]. Journal of Computational Information Systems , 2013, 9 (23) :9381–9388.
( 0) 0)
|
| [8] |
Szczytowski P, Khelil A, Suri N. DKM:distributed k-connectivity maintenance in wireless sensor networks[C]//20129th Annual Conference on Wireless on-Demand Network Systems and Services (WONS) 2012, 2012:83-90.
( 0) 0)
|


