针对自适应非线性流采样(DISCO)算法硬件实现面临的一系列挑战,设计了利于硬件处理的改进算法,采用多查找表结构和“归一化”方法进行处理,完成了正确性仿真和基于现场可编程门阵列(FPGA)平台的原型验证.实验结果表明,改进算法能够实现40 Gbit/s链路的线速每流统计,消耗FPGA上的硬件逻辑资源较少,并且平均相对误差和最大相对误差均与基准DISCO算法性能接近.
In flow-based passive measurement of the Internet, the measurement of flow size and flow volume is a basic requirement. To resolve the contradiction of increasing network link speed and small-sized fast memory chipset, a non-linear sampling algorithm which is named discrete counting (DISCO), was proposed in related research work. In order to meet the need of wire-speed network traffic measurement, DISCO is suggested to be implemented by hardware approaches, such as field-programmable gate array (FPGA). However, DISCO involves complex calculations with high precision, which give rise to a series of challenges in hardware acceleration. To solve the problems, a hardware-friendly refined algorithm was designed, which employs multiple lookup tables and a normalization method. Simulation was conducted to verify the validity of the refined algorithm. An FPGA-based prototype was made. Experiments show that the refined algorithm can achieve wire-speed flow measurement of a 40 Gbit/s link, with small hardware logic resources consumption of FPGA. The average relative error and maximum relative error of the refined DISCO algorithm are close to the original one.
网络测量对于网络计费、网络规划和网络安全等都十分重要,基于网络流的被动测量一直都是研究热点[1-2]. 随着网络链路速度的不断提高,对网络测量中流计数器所采用存储器的性能提出了更高的要求,基于动态随机存取存储器(DRAM,dynamic random access memory)的方案不再适用. 例如,在40 Gbit/s的链路中,如果考虑IP分组大小均为64 Bbit的最坏情况,每个IP分组留给测量模块的处理时间仅为12.8 ns,而DRAM的读写时延为数10 ns,不能满足需求. 基于DRAM的计数器方案被基于静态随机存取存储器(SRAM,static random access memory)的方案[1-2]取代. 但是,高速SRAM受其工艺和成本限制,容量很小. 主流的QDR II+ SRAM芯片容量仅为72 Mbit或者144 Mbit[3],远远小于DRAM,不能满足网络流数目的持续增大. 所以,如何能够在容量有限的SRAM上实现对百万条流的计数,成为一个重要的研究课题. 在基于SRAM的方案中,随机采样的方法[4]能够取得较好的压缩计数器大小的效果,但是却难以保证小流准确率. 而基于SRAM的DISCO[2]采用了非线性流采样算法,不仅计数器压缩率高,而且对大流和小流的测量误差都较小,给出了理论证明. 但是,自适应非线性流采样(DISCO)算法包含了较多高精度浮点运算,如果利用软件方法实现,难以满足高速链路的线速测量. 如果想要在现场可编程门阵列(FPGA,field-programmable gate array)硬件上实现DISCO算法并达到较高的测量速度,则需要重新设计改进算法,面临一系列的挑战.
1 硬件实现的挑战DISCO算法是一种用于流长度统计的概率计数算法. 该算法分为两部分:计数器更新部分和反向估计部分. 前者决定了对于长度为l的IP分组计数器增加的数值;后者通过最终计数器的数值来反向估计真实的流长度. DISCO算法的核心思想是使计数器的增量小于真实需要更新的数值,其大小是关于真实流长度(网络流的字节数和IP分组个数)在实数空间上的一个递增凹函数的数值. 对每个长度为l字节的分组,计数器的大小被增大了一个小于l的数值Δ. 然后,远端测量设备将计数器的值回导后进行处理,利用计数器的值c恢复出网络流的真实长度n,得到有效的测量结果. DISCO算法的计算公式为
| $f\left( c \right) = {{{b^c} - 1} \over {b - 1}}$ | (1) |
其中:b>1为一个预定义的参数;f(c)为一个递增的凸函数,其反函数f-1(c)是一个递增的凹函数. 流长度n和计数器值c的关系是n=f(c),这样计数器的增长将大大慢于线性增长. 对于到来的长度为 l的IP分组计数器值需要从c增加Δ(c,l)=f-1(l+f(c))-c,以便得到新的计数器值. 然而,作为计数器的SRAM没有足够的位宽来存储Δ(c,l)的小数部分. 如果简单使用四舍五入法来处理Δ(c,l)的小数部分将造成误差的累积,所以DISCO算法中还有一个基于概率的计数器更新算法,来防止误差累积. 当计数器值为c时,对于长度为l的分组,计数器将以pd(c,l)的概率增加δ(c,l)+1,以1-pd(c,l)的概率增加δ(c,l),其中:
| $\delta \left( {c,l} \right) = \left\lceil {{f^{ - 1}}\left( {l + f\left( c \right)} \right) - c} \right\rceil - 1$ | (2) |
| ${p_d}\left( {c,l} \right) = {{l + f\left( c \right) - f\left( {c + \delta \left( {c,l} \right)} \right)} \over {f\left( {c + \delta \left( {c,l} \right) + 1} \right) - f\left( {c + \delta \left( {c,l} \right)} \right)}}$ | (3) |
实现DISCO算法,需要对式(1)~(3)进行计算. 在硬件上对上述公式进行计算,常用的方法是利用只读存储器空间来换取计算时间,即将一些需要用到的计算结果做成查找表存入芯片的只读存储器中,通过查表来提高计算速度,简化计算过程,同时保证误差在允许的范围内. 其中,计算f(c)可以通过查表来实现. 若计数器c的位宽为12 bit,f(c)的位宽为32 bit,则f(c)查找表需要的存储资源为212×32 bit=128 Kbit,FPGA的片上逻辑资源能够满足. 而计算式(2)的δ(c,l)时,需要计算中间变量f-1(l+f(c))=logb[bc+(b-1)l] 的值. 若仍采用查表的方法,分组长度l可以取值64~1 500 B,有1 437种不同取值,f(c)有212=4 096种不同取值,组合起来有1 437×4 096个表项. 如果每个表项用32 bit存储,则存储f-1(l+f(c))相应的查找表需要1 437×4 096×32 bit≈180 Mbit的存储资源,FPGA的片上逻辑资源将难以满足. 对于式(3)的除法计算,通过类似的分析,也难以直接利用查找表实现.
若对于式(2)利用浮点数知识产权核来进行计算,则通过查阅相关资料[5],使用基于IEEE 754的双精度对数知识产权核来进行计算,在211 MHz(Stratix IV器件能够支持)下的时延是34个时钟周期,对于18 bit的数字信号处理器单元消耗为64个. 对于式(3),使用双精度除法知识产权核来进行计算,若不使用数字信号处理器单元,在267 MHz下的时延是61个时钟周期. 而且,若式(2)、式(3)采用双精度浮点数知识产权核进行计算,还需要涉及定点数到浮点数和浮点数到定点数的转换器,每一步转换都将消耗较多的时钟周期. 从消耗的时钟周期数来看,利用浮点数知识产权核不能实现线速测量.
2 改进算法的设计、仿真及分析针对DISCO算法硬件实现的复杂性,需要重新对式(1)~(3)进行分析,提出一个简洁的基于定点数运算和查表的改进算法,替代复杂的浮点数计算单元. 为此,提出了如下的改进算法.
首先,需要对b取值,此处取b=1+1/256(小数部分取2的幂方便进行移位操作). 并且,令a=f-1(l+f(c))=log b[(l+f(c))(b-1)+1],即a为式(2)中需要计算的中间变量. 令z=l+f(c)+1/(b-1),即z为a中对数的底数乘以1/(b-1). 在第1节对于式(2)中a=f-1(l+f(c))利用查表实现的分析,主要是由于存储开销过大导致查找表不可行,而查找表存储开销过大的原因来源于l和f(c)组合起来的表项数目过多. 对此,提出利用“归一化”的思想,将z先以2的倍数进行缩小(右移位操作),直到z进入0~1 024这个区间,以减小表项数;然后再加上缩小的部分,得到a的值. 对于式(3),则主要是除法运算实现困难. 对此,提出将除法运算转换为乘法运算来降低实现复杂度. 同时,当c>log bl时,δ(c,l)=0,因此可以提前判断c和log bl的大小关系,滤掉δ(c,l)=0时的后续计算,以提高系统性能. 综上,提出了改进算法如下,对上述3点问题进行了优化.
1查表获得log bl和f(c)的值;跳到第2步
2若
3计算z=l+f(c)+1/(b-1);跳到第4步
4令e=0;While(z≥1 024),{e++,z右移1位};跳到第5步
5计算a=log bz+(e-8)log b2,log bz和(e-8)log b2可以分别查表获得;跳到第6步
6计算δ(c,l)=a-c-1;跳到第7步
7计算pd的分子记为x,计算pd的分母与随机数的乘积记为y,比较两者的大小. 若x≥y,增加δ(c,l)+1;若x<y,增加δ(c,l)
在算法1中,需要实现f(c)、log bz和(e-8)×logb23个查找表,其中f(c)的存储开销为212×32 bit=128 kbit,log bz(位宽为12 bit,表示其整数部分)的开销为1 500×12 bit≈17.6 kbit,(e-8)log b2(位宽为12 bit,表示其整数部分)的开销为25×12 bit≈0.3 kbit. 3个表加起来的和小于150 kbit.
为了验证上述改进算法的正确性,对上述改进算法进行了C语言实现,并与利用双精度浮点数实现的基准DISCO算法进行了比较. 上述改进算法的C语言实现,完全仿照了FPGA中的寄存器传输级的特征,实现了3个查找表. 而双精度浮点数DISCO算法实现即将上述3个公式用双精度浮点数来进行计算,得到一个基准DISCO算法的结果.
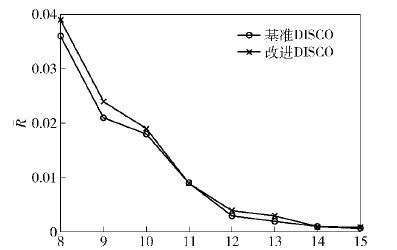
下面研究在输入真实流量的情况下,随着计数器位宽增大,基准DISCO算法和所提出的改进算法流量统计准确度的变化规律. 首先定义平均相对误差、最大相对误差两个参数. 相对误差R定义为流长度估计值 An^G2 和真实流长度n之差的绝对值比真实流长度,即R=| An^G2 -n|/n. 平均相对误差R定义为所有流计数器R值的平均值,它刻画了流量统计误差的平均情况. 最大相对误差Rmax 则定义为所有流计数器R值的最大值,它刻画了流量统计误差的最坏情况. 利用CAIDA上的一段1 min的OC-192的Trace[6]进行测试,仿真测试结果如图 1、图 2所示.
|
图 1 不同计数器位宽下的平均相对误差 |
|
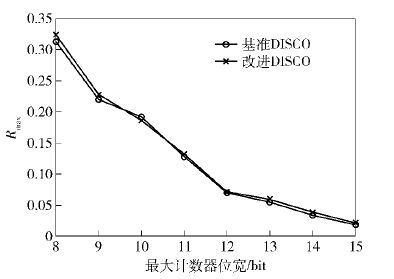
图 2 不同计数器位宽下的最大相对误差 |
从图 1和图 2中可以看出,平均相对误差R和最大相对误差Rmax均随着计数器位宽增大而逐渐减小. 这是因为随着计数器位宽增大,计满溢出的计数器个数显著减少,误差随之变小. 而当计数器位宽较大时,平均相对误差和最大相对误差的改善均十分有限,这是因为此时的误差主要是由于算法本身带来的统计误差,而非计数器溢出造成. 另一方面,从图 1和图 2中可以看出,改进算法和基准DISCO算法在平均相对误差和最大相对误差上十分接近,验证了改进算法的正确性.
此外,利用3种合成流量测试改进算法和基准DISCO算法在人工创造的极端流量条件下的平均相对误差. 3种合成流量分别服从帕累托分布、指数分布和均匀分布,与文献[2]中参数一致,而计数器位宽取为13 bit. 测试结果如表 1所示. 从表 1可以看出,在3种合成流量下,改进算法和基准DISCO算法在平均相对误差方面结果十分接近,进一步验证了改进算法在极端情况下的正确性.
|
|
表 1 3种合成分布下的平均相对误差 |
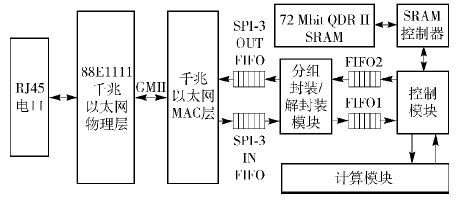
在FPGA实现中,不仅实现了DISCO的改进算法,也利用查找表的方式实现了非线性流采样(ANLS,adaptive non-linear sampling)算法[1]. 其中,利用DISCO的改进算法实现对分组字节数的统计;利用ANLS算法实现对分组个数的统计. 使用Altera Stratix IV E FPGA开发套件[7]作为实现改进的非线性采样流量统计算法DISCO的FPGA验证平台,测量系统如图 3所示.
|
图 3 基于FPGA的非线性流量统计系统原理 |
测量的流数据在服务器里封装成IP分组,通过千兆以太网传输到FPGA开发板上. 在FPGA开发板上,经过88E1111千兆以太网物理层芯片、千兆以太网介质访问控制(MAC,media access control)层之后,利用解封装模块将需要统计的网络流的流号、分组大小解析出来,送到FIFO1中. 控制模块从FIFO1中取到数据,利用SRAM中维护的计数器值和FIFO1中的数据,通过计算模块计算得到新的计数器值,并由控制模块写回到SRAM中. 当达到触发数据回导的条件后,控制模块将SRAM中的计数器数据回导到FIFO2中,通过分组封装模块封装成回导数据包,然后通过MAC层和物理层,最后利用千兆以太网将数据回导到服务器中. 服务器利用FPGA测量系统回导的数据,恢复真实的测量数据,并维护一张流表. 事实上,FPGA测量系统可以看作服务器的一个协处理器,它们之间利用千兆以太网接口相连(另一种实现方案也可以选择PCI-E接口).
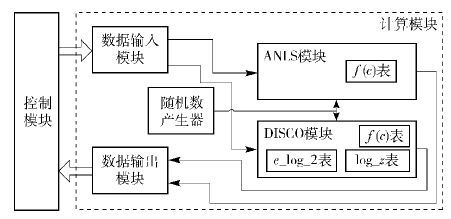
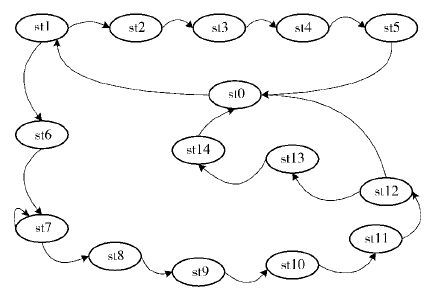
下面主要关注计算模块的实现. 计算模块的结构如图 4所示. 其中,随机数产生器利用32 bit的线性反馈移位寄存器来实现. 数据输入模块和数据输出模块主要对输入/输出数据进行格式转换、解析和封装. ANLS模块利用一张f(c)查找表实现,比较简单. DISCO模块利用3张查找表实现,具体的状态机如图 5和表 2所示. 该状态机严格按照第2节的改进算法进行设计.
|
图 4 计算模块结构 |
|
图 5 DISCO模块状态机示意图 |
|
|
表 2 DISCO模块状态机功能表 |
首先,按照FPGA工程的开发流程,对工程利用Modelsim进行功能仿真. 其中,在时序仿真中,利用TimeQuest工具测试,工程能够稳定工作在150 MHz. 然后,将verilog HDL代码编译生成的电路通过Jtag接口下载到了FPGA中,在服务器端利用Libnet软件发送测量请求包,利用Libpcap接收回导的包,并且在PC服务器上维护一个活跃流流表. 在FPGA端用Signaltap II逻辑分析仪进行测试,验证FPGA端的数据通路.
最后,定量分析在FPGA上实现的改进DISCO算法,在FPGA上实现的基于浮点数知识产权核的基准DISCO算法(记为知识产权核DISCO算法)以及在通用服务器上软件实现的基准DISCO算法(记为软件DISCO算法)在处理性能和消耗资源两个方面的指标. 其中,实验平台参数与实验方法如表 3所示.
|
|
表 3 实验平台参数与实验方法对比 |
第一,对于实验平台参数,改进DISCO和知识产权核DISCO算法均是以Stratix IV E开发板为基准,而软件DISCO算法则使用了一台通用服务器(CPU为i7 3770 3.4 GHz,内存为32 GB DDR3)实现. 第二,对于处理性能指标,此处取为吞吐率,单位为Mpacket/s. 其中,改进DISCO算法处理性能是系统时钟为150 MHz时,通过统计计算模块消耗的最大时钟周期数得到;知识产权核DISCO算法的执行时间近似为对数知识产权核与除法知识产权核消耗时钟周期数之和(假设时钟频率也为150 MHz),通过查找手册[5]得到;软件DISCO算法消耗时间通过C/C++中的clock( )函数统计得到. 第三,对于资源消耗指标,改进DISCO算法的资源消耗取自Quartus II编译后的报告,单位是消耗的ALUT个数;知识产权核DISCO算法的资源消耗通过查找手册[5]得到,为对数知识产权核与除法知识产权核消耗ALUT数之和;软件DISCO算法实现消耗服务器内存资源和CPU计算资源不会成为性能瓶颈,在此没有考虑. 对于处理性能和消耗资源两个方面指标的实验与分析结果如表 4所示. 通过表 4可以得出,改进DISCO算法与知识产权核DISCO和软件DISCO算法相比,在处理性能和资源消耗上都有优势.
|
|
表 4 执行时间与资源消耗对比 |
利用表 4的处理性能数据,可算出改进DISCO算法实现的计算模块支持的带宽. 若假设到达的数据分组大小均为64 B的最坏情况,改进DISCO算法实现的计算模块最大支持带宽为B=64×8 bit/packet×10.714 Mpacket/s≈5 485.6 Mbit/s. 同时,例化8个上述计算模块,利用负载均衡的方法,将需要统计的网络流分为8部分,交由8个计算模块进行处理,最大支持带宽可达到40 Gbit/s.
4 结束语自适应非线性流采样算法DISCO是一种网络流测量的优秀算法,但是在硬件实现上面临一系列的挑战. 笔者提出了一种面向FPGA硬件实现的DISCO改进算法,利用多查找表结构和“归一化”处理,克服了标准DISCO算法在硬件实现中的问题. 仿真实验结果证明,改进算法在性能和正确性方面和基准DISCO算法接近. 并且,基于FPGA的原型系统实现验证了改进算法的有效性,能够满足40 Gbit/s线速测量要求,也对相关流量统计算法的硬件实现有较强的借鉴意义.
| [1] |
Hu Chengchen, Wang Sheng, Tian Jia, et al. Accurate and efficient traffic monitoring using adaptive non-linear sampling method[C]//Proc of the IEEE INFOCOM 2008. Piscataway, NJ:IEEE, 2008:26-30.
( 0) 0)
|
| [2] |
Hu Chengchen, Liu Bin, Zhao Hongbo, et al. DISCO:memory efficient and accurate flow statistics for network measurement[C]//Proc of the IEEE ICDCS 2010. Piscataway, NJ:IEEE, 2010:665-674.
( 0) 0)
|
| [] |
QDR Consortium. QDR technology and product family[EB/OL].[2014-11-20]. http://www.qdrconsortium.org/qdr-product-family.htm.
( 0) 0)
|
| [4] |
Estan C, Keys K, Moore D, et al. Building a better netflow[C]//Proc of the ACM SIGCOMM 2004. New York:ACM, 2004:245-256.
( 0) 0)
|
| [5] |
Altera Corporation. Altera floating-point megafunctions user guide 11. 1[R]. San Jose, CA:Altera Corporation, 2011.
https://www.altera.co.jp/ja_JP/pdfs/literature/ug/ug_altfp_mfug.pdf ( 0) 0)
|
| [6] |
The cooperative association for internet data analysis. CAIDA Dataset[EB/OL].[2014-9-11]. http://www.caid-a.org/data/.
( 0) 0)
|
| [7] |
Altera Corporation. Altera Stratix IV E FPGA development kit[EB/OL]. San Jose, CA:Altera Corporation, 2014(2014)[2014-11-20]. http://www.alter-a.com/products/devkits/altera/kit-stratix-iv-e.html.
( 0) 0)
|


