2. 河北工程大学 信息与电气工程学院, 河北 邯郸 056038
针对无线传感器网络(WSN)中,经过多跳路由传输训练数据到数据中心进行集中式训练时存在的高数据通信代价问题,基于L1正则化的稀疏特性,研究了仅依靠邻居节点间的协作,在网内分布式协同训练核最小均方差(KMSE)学习机的方法.首先,在节点模型与邻居节点间局部最优模型对本地训练样本预测值相一致的约束下,利用并行投影方法和交替方向乘子法对L1正则化KMSE的优化问题进行稀疏模型求解;然后,当各节点收敛到局部稳定模型时,利用平均一致性算法实现各节点稀疏模型的全局一致.基于此方法,提出了基于并行投影方法的L1正则化KMSE学习机的分布式(L1-DKMSE-PP)训练算法.仿真实验结果表明,L1-DKMSE-PP算法能够得到与集中式训练算法相当的预测效果和比较稀疏的预测模型,更重要的是能显著降低核学习机训练过程中的数据通信代价.
2. School of Information and Electrical Engineering, Hebei University of Engineering, Hebei Handan 056038, China
In wireless sensor network (WSN), the centralized learning method by transmitting all training samples scattered across different sensor nodes to a centralized data center to train classifier will significantly increase the communication cost. To decrease the communication cost in transmitting training samples, a distributed learning method for kernel minimum squared error (KMSE) by incorporating L1 regularized term was studied, which just relies on in-network processing between single-hop neighboring nodes. Each node obtains its local optimum sparse model by constructing the optimization problem of L1 regularized KMSE based on its local training samples and solving it using parallel projections and alternating the direction method of multipliers, then a consistent model is achieved on all nodes by using the global average consensus algorithm. For carrying out this method,a new distributed training algorithm for L1-regularized kernel minimum squared error based on parallel projections (L1-DKMSE-PP) was proposed. Simulations show that L1-DKMSE-PP can obtain almost the same prediction accuracy as that of the centralized counterpart and a sparser model, and more importantly, it can significantly reduce the communication cost.
在无线传感器网络(WSN,wireless sensor network)的众多应用中,对监测信息进行分类是最基础也是最重要的一项任务[1-2]. 核学习机(或核方法)作为解决分类问题的主流方法,在WSN中得到了日益广泛的应用[3]. 然而,在WSN中训练数据都分散在各节点上,通过多跳路由将所有训练数据传输到数据中心进行集中式训练,将会消耗大量的节点能量、占用大量的带宽,这与WSN上能源替换代价非常高甚至不可替换、带宽资源非常有限相冲突,同时也容易使数据中心周围节点成为整个系统的瓶颈. 因此,通过相邻节点间的协作,利用节点本身的处理能力,在网内分布式协同学习核分类器的方法引起了众多学者的关注和研究[4-6]. 但是,已有的WSN下核学习机分布式训练方法仍存在构建或维护特定链路代价高、基于共享数据普适性不强和支持向量机(SVM,support vector machine)增量训练通信代价大等问题. 为此,笔者以核最小平方误差(KMSE,kernel minimum squared error)方法和具有稀疏特性的L1正则化相结合,研究了仅依靠相邻节点间的协作,在网内分布式协同训练L1正则化KMSE学习机的方法,提出了基于并行投影方法的L1正则化KMSE学习机分布式(L1-DKMSE-PP,L1-regularized distributed kernel minimum squared error based on parallel projections)训练算法.
1 预备知识考虑二分类问题,给定一组独立同分布的训练样本集S={(xi,yi),xi∈Rd,yi∈{-1,1},i=1,2,…,m}. 基于“损失函数+正则项”框架的KMSE分类问题可以归结为求解优化问题:
| $\mathop {min}\limits_{f \in {H_K}} {1 \over m}\sum\limits_{i = 1}^m {{{({y_i} - f({x_i}))}^2} + \Omega ({{\left\| f \right\|}_{{H_K}}})} $ | (1) |
其中:f∈HK为再生希尔伯特空间中的函数;f(xi)为对样本xi的期望输出;Ω(‖f‖HK)为正则项,用于避免模型过拟合. 表示定理给出了式(1)中最优函数f*(·)的表示形式[3]为
| ${f^*}\left( \cdot \right) = \sum\limits_{i = 1}^m {{\alpha _i}k({x_i},\cdot)} $ | (2) |
其中:k(xi,·)为已知样本xi与未知样本的向量内积,用于描述两个样本间的相似程度或距离大小;αi∈R(i=1,2,…,m)为k(xi,·)的系数. 由式(2)可以看出,核学习机f*(·)依赖训练样本数据.
为了说明WSN中各节点之间的相邻关系,使用无向图G(J,E)对WSN进行描述,J为节点集合,E为节点间直接通信的链路集合,每个节点j∈J及其单跳邻居节点用集合Bj⊆J来表示. 假定网络是连通的,即网络中任意两点间至少存在一条路径. 每个节点j上的训练数据集用Sj:={(xjn,yjn),n={1,2,…,Nj}}表示,其中xjn∈Rd为训练数据jn的特征向量,d为特征向量维数,yjn∈{1,-1}为训练数据jn对应的类别标签,Nj为训练数据数量. 另外,模型训练之前,相邻节点间没有相同的训练数据.
为方便描述,给出以下两个定义:
定义1(关键样本) 模型系数解向量中非零项对应的训练样本,称为关键样本.
定义2(模型稀疏率) 模型中关键样本数与参与模型训练的总样本数的比值,称为模型稀疏率.
2 L1 KMSE学习机分布式训练方法为减少f*(·)依赖的训练样本数量,利用L1正则化构建KMSE学习机优化问题:
| $\mathop {min}\limits_{f \in {H_K}} {1 \over m}\sum\limits_{i = 1}^m {{{({y_i} - f({x_i}))}^2} + \lambda ({{\left\| f \right\|}_1})} $ | (3) |
其中:λ‖f‖1为正则项,λ>0为正则项系数.
2.1 L1 KMSE学习机训练问题的推导为减少L1正则化KMSE学习机分布式训练过程中的数据传输量,借鉴文献[7]中基于一次全局平均一致性线性SVM分布式训练算法1-AC-DSVM的思想,构建基于节点本地模型与局部最优模型对本地训练样本预测值一致的优化问题:
| $\eqalign{ & \mathop {min}\limits_{{f_j} \in {H_K}} {1 \over {{N_j}}}\sum\limits_{n = 1}^{{N_j}} {{{({y_{jn}} - {f_j}({x_{jn}}))}^2} + \lambda {{\left\| {{f_j}} \right\|}_1}} \cr & s.t.{f_j}({x_{jn}}) = \bar f_{{B_j}}^*({x_{jn}}),\forall j \in J,n = 1,2, \ldots ,{N_j} \cr} $ | (4) |
其中:Nj为节点j∈J上参与训练的样本数量,fBj**(xjn)为节点j及其邻居节点间的局部最优模型对本地训练样本的预测值. 为求解式(4)的优化问题,每个节点j∈J利用并行投影方法对其等式约束构建优化问题,如式(5)所示,相应的求解迭代形式如式(6)和式(7)[8]所示.
| $\eqalign{ & min{1 \over {{N_j}}}\sum\limits_{n = 1}^{{N_j}} {{{({y_{jn}} - {f_j}({x_{jn}}))}^2} + \lambda {{\left\| {{f_j}} \right\|}_1}} + \cr & {1 \over 2}\left\| {{f_j}} \right.({x_{jn}}) - \bar f_{{B_j}}^*\left. {({x_{jn}})} \right\|_2^2,\forall j \in J,n = 1,2, \ldots ,{N_j} \cr} $ | (5) |
| $\bar f_{{B_j}}^{{*^{k + 1}}}({x_{jn}}) = {{\sum\limits_{i = 1}^{{B_j}} {f_i^{k + 1}({x_{jn}})} } \over {\left| {{B_j}} \right|}},\forall j \in J,n = 1,2, \ldots ,{N_j}$ | (6) |
| $\eqalign{ & \sum\limits_{i = 1}^{{B_j}} {f_i^{k + 1}({x_{jn}})} = \cr & \arg \min \left\{ {{1 \over {{N_j}}}} \right.\sum\limits_{n = 1}^{{N_j}} {{{({y_{jn}} - {f_j}({x_{jn}}))}^2} + \lambda {{\left\| {{f_j}} \right\|}_1}} + \cr & {1 \over 2}\left\| {{f_j}} \right.({x_{jn}}) - \bar f_{{B_j}}^*\left. {({x_{jn}})} \right\|\left. {_2^2} \right\},\forall j \in J,n = 1,2, \ldots ,{N_j} \cr} $ | (7) |
式(6)中:|Bj|为Bj中元素个数,即节点j及其邻居节点数量;fBj**k+1(xjn)为节点j的局部最优模型对其本地样本的预测值,是包括j在内的所有邻居节点的模型对节点j本地训练样本预测值的平均. 式(7)是一个无约束优化问题,求解该优化问题,利用交替方向乘子方法将其变换成等价的含有等式约束的优化问题[8],如式(8)所示.
| $\eqalign{ & \min {1 \over {{N_j}}}{({Y_j} - {K_j}{\alpha _j})^T}({Y_j} - {K_j}{\alpha _j}) + \cr & {1 \over 2}\left\| {{K_j}{\alpha _j}} \right. - \bar f_{{B_j}}^*\left. {({x_{jn}})} \right\|_2^2 + \lambda {\left\| {{z_j}} \right\|_1} \cr & s.t.{\alpha _j} - {z_j} = 0 \cr} $ | (8) |
其中:Yj为训练样本类别标签向量,Kj为由本地训练样本通过核函数k(xi·xj)得到的增广核矩阵,αj为要求解的系数向量. 利用交替方向乘子方法对式(8)进行推导求解,得到各变量的迭代形式,如式(9)~式(11)所示.
| $\eqalign{ & \alpha _j^{k + 1} = {\left[ {\left( {{2 \over {{N_j}}} + 1} \right)K_j^T{K_j} + \rho I} \right]^{ - 1}} \cr & \left[ {K_j^T\left( {{2 \over {{N_j}}}{Y_j} + \bar f{{_{{B_j}}^*}^k}({x_j})} \right) + \rho (z_j^k + u_j^k)} \right] \cr} $ | (9) |
| $z_j^{k + 1}: = {\Psi _{\lambda /\rho }}(\alpha _j^{k + 1} + u_j^k)$ | (10) |
| $u_j^{k + 1}: = u_j^k + \alpha _j^{k + 1} - z_j^{k + 1}$ | (11) |
式(9)中:ρ为大于0的常数,uj为对偶变量. 式(10)中的Ψ为软阈值操作符,其定义为
| ${\Psi _k}\left( a \right) = \left\{ {\matrix{ {a - k} & {a > k} \cr 0 & {\left| a \right| \le k} \cr {a + k} & {a < - k} \cr } } \right.$ | (12) |
各节点利用式(9)~式(11)可以求得系数向量αj,进而求出本地最优稀疏模型,如式(13)所示,其中l为系数向量αj中非零项的个数.
| $f_j^{k + 1}\left( \cdot \right) = \sum\limits_{i = 1}^l {\alpha _i^{k + 1}k({x_i},\cdot),\forall j \in J} $ | (13) |
至此,各节点按照式(9)~式(11)、式(13)、式(6)的顺序迭代求解节点本地最优稀疏模型.
2.2 邻居节点间的协作式(9)中,fBj*(xj)是节点j及其邻居节点模型对其本地训练样本预测得到的平均预测值.为了得到该平均预测值,节点j需要得到所有邻居节点的稀疏模型,即邻居节点间需要以传输稀疏模型的方式进行协作. 为充分发挥稀疏模型在节点模型求解过程中的作用,各节点接收到邻居节点发送过来的稀疏模型后,先将稀疏模型中的关键样本加入到本地训练样本集,然后利用接收到的模型对本地训练样本计算平均预测值. 为减少数据传输量,各节点对已经发送过的训练样本设置发送标志,限制其重复发送. 当各节点以此协作方式收敛到本地最优稀疏模型后,邻居节点间仍依靠传输稀疏模型的方式,利用平均一致性算法实现各节点模型的全局一致.
2.3 L1正则化KMSE学习机分布式训练算法基于上述迭代形式和邻居节点间的协作方式,提出了L1-DKMSE-PP训练算法,其步骤如下.
算法:L1-DKMSE-PP
输入:初始化节点j∈J上的训练样本集Sj:={(xjn,yjn),n={1,2,…,Nj}}、核参数σ、正则系数λ、k=0、fBj*k(xjn)=yjn;
输出:稀疏模型f*(·);
重复:
步骤1 k=k+1,节点j利用式(9)~式(11)、式(13)求出局部稀疏模型fjk(·),并发送给邻居节点.
步骤2 节点j接收邻居节点的稀疏模型fik(·),i∈Bj,并将其中的关键样本加入到本地训练样本集;然后利用接收到的所有模型对本地训练样本进行预测,利用式(6)求出fBj*k(xj).
步骤3 当k≥2时,节点j判断局部模型是否满足收敛条件,若不满足,重复步骤1~3;若满足,结束,转步骤4.
步骤4 利用平均一致性算法对节点收敛到的局部最优模型进行全局平均,得到最优模型f*(·).
3 仿真实验与结果分析为了验证算法L1-DKMSE-PP的有效性,以一个由30个节点构成的WSN为例,使用模拟数据集和(UCI,UC irvine machine learning repository)基准数据集进行实验,并与L1正则化KMSE学习机的集中式(L1-CKMSE,centralized KMSE based on L1 regularized)训练算法、SVM的集中式(CSVM,centralized support vector machine)训练算法、文献[4]中的分布式训练算法(AP-DKMSE,distributed KMSE based on alternative projection)和文献[6]中的分布式训练算法(DPSVM,distributed parallel support vector machine)从模型预测正确率、模型稀疏率和数据传输量3个方面进行对比.
3.1 实验设置本实验中模拟数据集由两类非线性可分的数据组成,一类服从均值为mu1=[0,0]T、协方差矩阵为Σ=[0.6,0;0,0.4]T的二维高斯分布,另一类服从混合参数分别为π1=0.3和π2=0.7、均值分别为mu2=[-2,-2]T和mu3=[2,2]T、协方差矩阵均为Σ的二维混合高斯分布;UCI基准数据集是wave-form和wave-form-noise. 3个数据集的基本信息如表 1所示.
|
|
表 1 数据集基本信息 |
实验中核函数选用高斯核函数k(xi,xj)=exp(-‖xi-xj‖2/2σ2),*算法CSVM、L1-CKMSE、L1-DKMSE-PP、AP-DKMSE和DPSVM使用的核参数σ、正则系数λ以及惩罚因子C的参数值,使用搜索方法寻优得到. 各算法在3个数据集上使用的参数值如表 2所示. 基于上述实验设置,在每个数据集上进行30次独立实验.
|
|
表 2 数据集实验参数值 |
1) 模型预测正确率
如图 1所示,算法L1-DKMSE-PP在synthetic dataset、wave-form和wave-form-noise数据集上的模型预测正确率与集中式算法L1-CKMSE表现基本一致,与其他对比算法CSVM、AP-DKMSE和DPSVM相比也都没有明显差别.
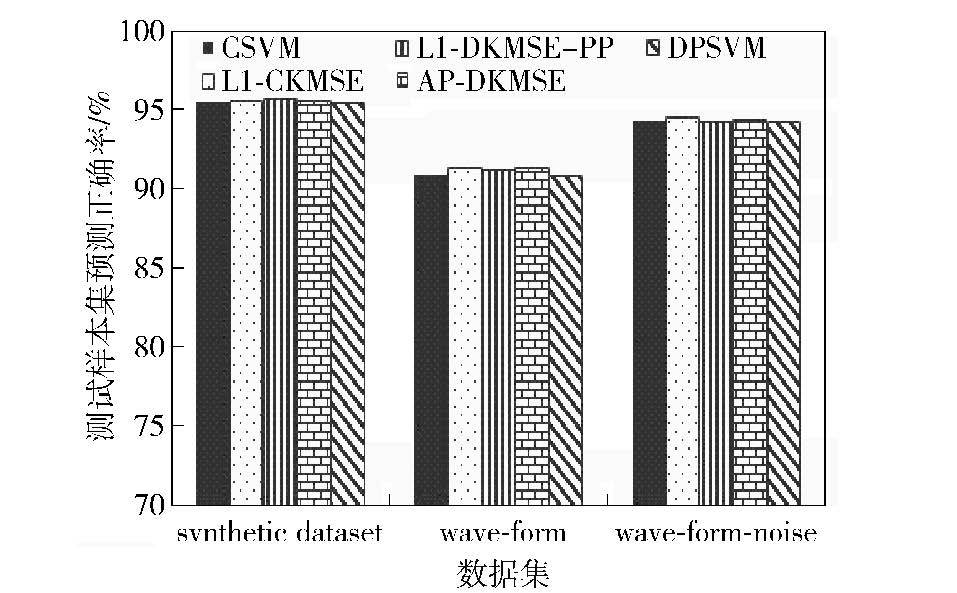
|
图 1 不同算法在3个数据集上的模型预测正确率对比 |
2) 模型稀疏率
如图 2所示,在synthetic dataset、wave-form和wave-form-noise上,算法L1-DKMSE-PP在模型稀疏率上均明显高出了集中式算法L1-CKMSE,但都显著低于集中式算法CSVM、分布式算法AP-DKMSE和DPSVM. 这表明,算法L1-DKMSE-PP在3个数据集上的模型稀疏效果显著优于对比算法CSVM、AP-DKMSE和DPSVM,但也明显略劣于集中式算法L1-CKMSE.
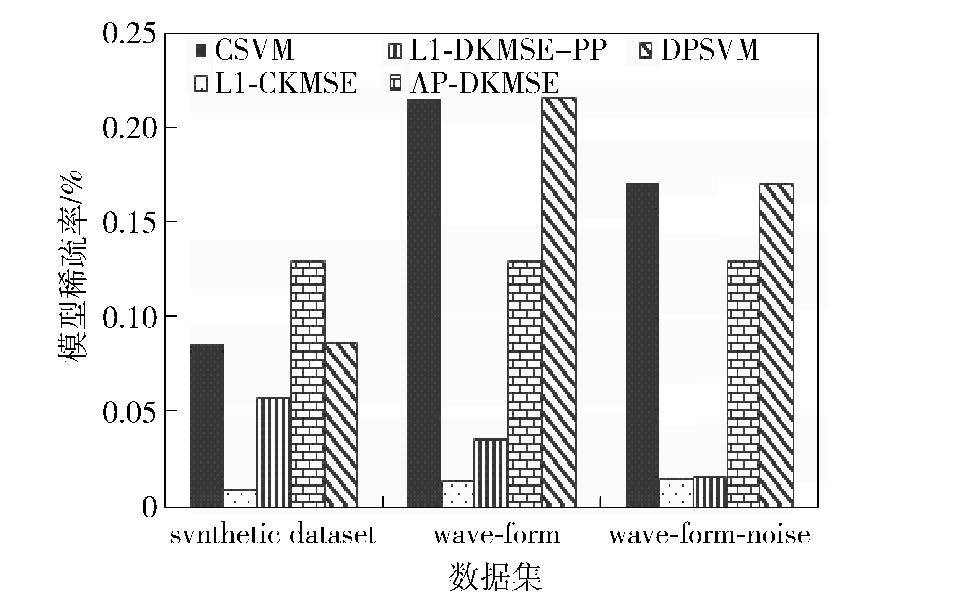
|
图 2 不同算法在3个数据集上的模型稀疏率对比 |
3) 数据传输量
如图 3所示,在synthetic dataset上,算法L1-DKMSE-PP的数据传输量与集中式算法CSVM和L1-CKMSE相比,分别少37.94%和32.38%;与分布式算法AP-DKMSE相差更明显,少了69.41%,但与分布式算法DPSVM相比,多了12.57%. 在wave-form和wave-form-noise上,算法L1-DKMSE-PP的数据传输量均显著低于其他4个对比算法. 在synthetic dataset和UCI的2个基准数据集上,算法L1-DKMSE-PP和DPSVM在数据传输量上对比结论不一致,其原因是算法DPSVM在不同数据集上表现出极其不同的稀疏特性,在synthetic dataset上,算法DPSVM的模型稀疏程度很大,而在UCI的2个基准数据集上表现很差,所以,算法DPSVM的模型稀疏率和数据传输量受训练样本集影响很大. 而算法L1-DKMSE-PP在模型稀疏率和数据传输量上受不同数据集影响不明显,并且在3个数据集上的数据传输量均显著低于对比算法L1-CKMSE、CSVM和AP-DKMSE.
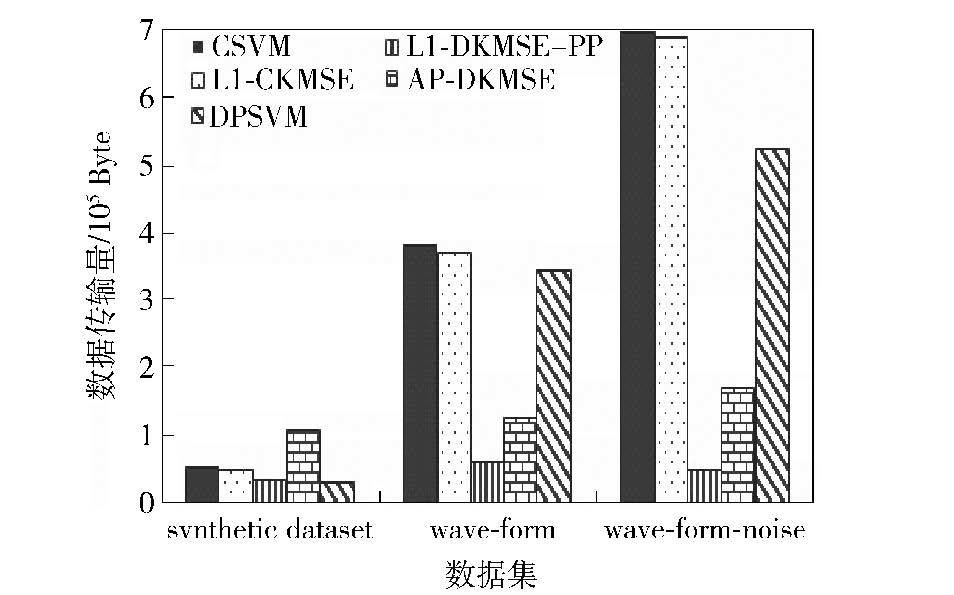
|
图 3 不同算法在3个数据集上的数据传输量对比 |
针对WSN中集中式训练核学习机时存在的数据传输代价大的问题,研究了仅依靠相邻节点间的协作在网内分布式协同训练方法,提出了仅依靠相邻节点间传输稀疏模型的协作方式,在网内分布式协同训练L1正则化KMSE学习机的算法L1-DKMSE-PP. 仿真实验结果表明,在模型预测正确率上,算法L1-DKMSE-PP取得了与集中式算法L1-CKMSE和其他对比算法相当的预测效果;在模型稀疏率上,算法L1-DKMSE-PP仅次于其对应的集中式算法L1-CKMSE,但明显优于实验中其他对比算法;在数据传输量上,算法L1-DKMSE-PP较实验中的对比算法L1-CKMSE、CSVM和AP-DKMSE都表现出绝对优势. 算法L1-DKMSE-PP因其在数据传输量上的显著优势,为WSN下进行核学习机的训练提供了一种可行的方法.
| [1] |
Taghvaeeyan S, Rajamani R. Portable roadside sensors for vehicle counting, classification, and speed measurement[J]. IEEE Transactions on Intelligent Transportation Systems , 2014, 15 :73–83.
doi:10.1109/TITS.2013.2273876 ( 0) 0)
|
| [2] |
韩屏, 李方敏, 罗婷. 无线传感器网络的分布式目标跟踪算法[J]. 北京邮电大学学报 , 2009, 32 (1)
:90–94.
Han Ping, Li Fangmin, Luo Ting. Distributed target tracking algorithm for wireless mobile sensor networks[J]. Journal of Beijing University of Posts and Telecommunications , 2009, 32 (1) :90–94.
( 0) 0)
|
| [3] |
Scholkopf B, Smola A.
Learning with kernels:support vector machines, regularization, optimization and beyond[M]. England: The MIT Press , 2002 : 61 -118.
( 0) 0)
|
| [4] |
Predd J B, Kulkarni S R, Poor H V. A collaborative training algorithm for distributed learning[J]. IEEE Transactions on Information Theory , 2009, 55 (4) :1856–1870.
doi:10.1109/TIT.2009.2012992 ( 0) 0)
|
| [5] |
Flouri K, Beferull-Lozano B, Tsakalides P. Optimal gossip algorithm for distributed consensus SVM training in wireless sensor networks[C]//DSP 2009. Santorini-Hellas:IEEE, 2009:886-891.
( 0) 0)
|
| [6] |
Lu Yumao, Roychowdhury V, Vandenberghe L. Distributed parallel support vector machines in strongly connected networks[J]. IEEE Transactions on Neural Networks , 2008, 19 (7) :1167–1178.
doi:10.1109/TNN.2007.2000061 ( 0) 0)
|
| [7] |
及歆荣, 侯翠琴, 侯义斌. 无线传感器网络下线性支持向量机分布式协同训练方法研究[J]. 电子与信息学报 , 2015, 37 (3)
:708–714.
Ji Xinrong, Hou Cuiqin, Hou Yibin. Research on the distributed training method for linear SVM in WSN[J]. Journal of electronics & information technology , 2015, 37 (3) :708–714.
( 0) 0)
|
| [8] |
Boyd S, Parikh N, Chu E. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning , 2011, 3 (1) :1–122.
( 0) 0)
|


