提出了一种调节视频分块在时间轴上分布集中的视频块调度算法,满足了用户能快速接收时间轴上随机分布、内容上连续且数量较多的视频段的需求,从而使用户在短时间内了解初始视频的有效内容.该算法可有效引导视频块的传输,大大降低递交延时.实验结果表明,视频分块调度算法有效可行.
An algorithm of randomly intensive dissemination of video fragments in opportunistic network was proposed to satisfy the requirement of more number of video segments distributed randomly in time axis and sequenced in content so that users can acquire effective information of the original video. The proposed algorithm can guide transportation of video blocks while delivery delay is reduced sharply. Simulations show that random-sequential content spreading (RSCS) significantly outperforms these approaches in terms of random-sequential index. Moreover, RSCS also achieves better performance levels in ratio of delivery and latency than sequential solution.
大数据时代,基于机会网络通信的数据分发和检索[1]以及面向多媒体应用的机会网络视频传输方法逐渐成为当前研究的新课题. 多样的移动终端能产生不同类型的多媒体数据,并以多种路由算法[2-6]和数据调度算法在节点间传输,Mavromoustakis等[7]提出了面向通信量的路由算法.
机会网络节点间的通信有机会性和时效性,一个大的视频数据很可能在节点间尚未传输完成时就发生连接中断. 而在短时间内,用户最大的需求是快速地了解初始视频整体的内容,而并不过多关注某个时间段的更为具体的信息. 因此,节点在视频分块接收不完整情况下,要让用户在短时间内了解视频的有效信息,就要求在有限时间内接收到的视频分块应尽可能在内容上连续,且这些连续的视频段尽可能随机分布于时间轴.
笔者提出了随机集中调度算法(RSCS,random-sequential content spreading),通过有目的地调度,能使用户在短时间内接收的视频分块尽可能地在时间轴上随机地集中,从而给用户在短时间内提供有效的视频信息,使用户可在短时间内了解初始视频的有效内容,较好地满足用户的需求,使用户有较好的浏览体验.
1 视频块分发分析为了有效引导视频块的排列方式,就需要研究初始大容量视频的分割方法和节点间视频块交换时的分块选择算法.
首先,源节点待发送的视频文件较大,必须对该视频文件进行分块,以便在延迟容忍网络(DTN,delay tolerant network)传输. 且初始视频文件在分块后,必须能独立进行播放.
其次,完成大视频数据的分块之后,源节点和中继节点在相遇的过程中将不同编号的视频块转发给中继节点,这些视频分块被存放在节点的缓冲区中,并形成一个视频块序列,如图 1所示.

|
图 1 视频块序列 |
图 1中阴影部分表示已经接收的视频块,空白部分表示尚未接收的视频块. 很明显,接收到的视频块有的连续排列,有的分散排列. 中继节点或目的节点为了能流畅地播放已有的视频数据,需满足2个条件:第一,分块越多越好;第二,已经接收的分块越连续越好. 因此,影响任何一个待接收视频块的因素有以下几点:待接收的视频块所在的组在整个缓冲区中的位置,待接收视频块所在的组的长度,待接收视频块在所在组中的位置,待接收视频块所在区域中已接收视频块对待接收视频块的影响.
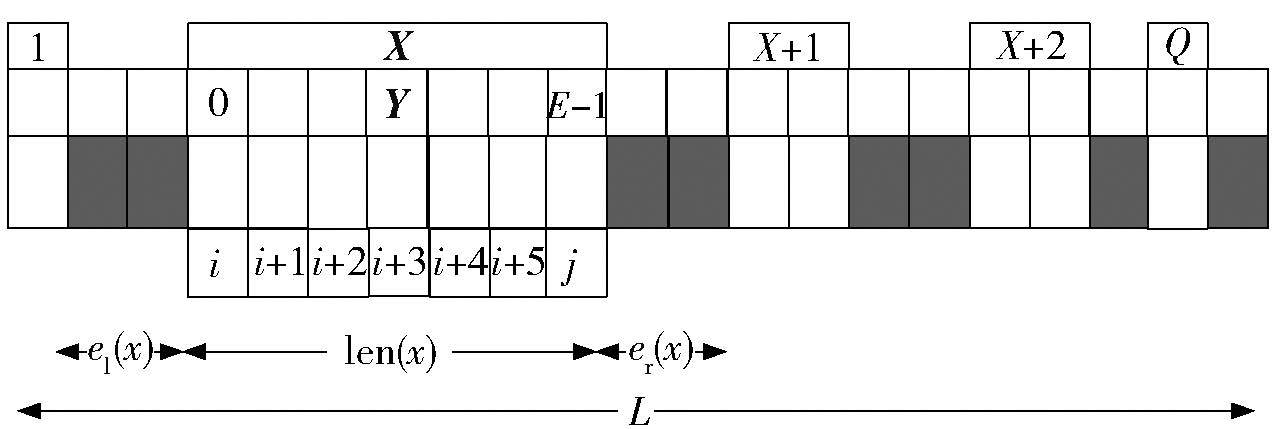
2 RSCS算法 2.1 视频块优先级和随机集中度节点接收的这些视频分块被存放在各自的缓冲区中,并形成一个视频块序列,如图 2所示.
|
图 2 视频块缓冲区 |
图 2的视频分块序列中,每一个视频分块都有一个传输优先级,也即集中紧缺程度. 发送节点中待发送分块的紧缺度等于接收节点中等待接收分块(空白分块)的紧缺度,笔者提出的集中紧缺程度的计算式为
| ${h_{weight}}\left( {x,y} \right) = {{P\left( {x,y} \right)I\left( {x,y} \right)} \over {L\left( {x,y} \right)}}S\left( {x,y} \right)$ | (1) |
| $P\left( {x,y} \right) = {{{e_l}\left( x \right) + {e_r}\left( x \right)} \over {len\left( x \right)}}$ | (2) |
| $L\left( {x,y} \right) = len\left( x \right)$ | (3) |
| $I\left( {x,y} \right) = \left\{ {\matrix{ {f\left( {y - \left( {{{i + j} \over 2} + 1} \right)} \right),i \le y \le {{i + j} \over 2},len\left( x \right),} \cr {为偶数} \cr {f\left( {y - \left( {{{i + j} \over 2}} \right)} \right),{{i + j} \over 2} + 1 \le y \le j,} \cr \matrix{ len\left( x \right)为偶数 \hfill \cr f\left( {y - \left( {{{i + j} \over 2}} \right)} \right),i \le y \le j,len\left( x \right)为奇数 \hfill \cr} \cr } } \right.$ | (4) |
| $f\left( z \right) = \left\{ \matrix{ - z, - {L \over 2} \le z < 0 \hfill \cr 0,z = 0 \hfill \cr z,0 < z \le {L \over 2} \hfill \cr} \right.$ | (5) |
| $\eqalign{ & S\left( {x,y} \right) = \cr & \sum\limits_{k = \left( {y + 1} \right) - {L \over 2}}^{y + {L \over 2}} {\left( {g\left( {x,k - \left[ {\left( {y + 1} \right) - {L \over 2}} \right]} \right)} \right)} \neg \left( k \right) \cr} $ | (6) |
| $g\left( {x,y} \right) = \left\{ \matrix{ y,0 \le y < {L \over 2} \hfill \cr L - y,L/2y \le L \hfill \cr 2L - y,{L \over 2} \le y \le L \hfill \cr} \right.$ | (7) |
为了评价RSCS算法的性能,笔者提出随机集中度的计算式为
| $\eqalign{ & P = \cr & {{\sum\limits_{y = 0}^{{E_x} - 1} {\left( {\sum\limits_{k = \left( {y + 1} \right) - {L \over 2}}^{y + {L \over 2}} {\left( {\sigma \left( {k - \left[ {\left( {y + 1} \right) - {L \over 2}} \right]} \right)\neg Exist\left( k \right)} \right)} } \right)} } \over M} \cr} $ | (8) |
σ(y)的计算式为
| $\sigma \left( y \right) = \left\{ \matrix{ y,0 \le y < {L \over 2} \hfill \cr L - y,L/2 < y \le L \hfill \cr L - y,{L \over 2} \le y \le L \hfill \cr} \right.$ | (9) |
其中:hweight(x,y)为视频分块的集中紧缺度;P(x,y)为第x个空白分块组中下标为y的空白分块的中心优先级,L(x,y)为第x个空白分块组中下标为y的空白分块的长度优先级,I(x,y)为第x个空白分块组中下标为y的空白分块的位置优先级,S(x,y)为第x个空白分块组中下标为y的空白分块的区域优先级.
x为空白分块组的组号,x∈[1,Q],Q为空白分组的总数;y为空白分块组内空白分块的相对下标,y∈[0,Ex-1],Ex为第x个空白分组中的空白分块的总数;el(x)为第x个空白分组的左邻接非空分块组的长度,er(x)为第x个空白分组的右邻接非空分块组的长度,len(x)为第x个空白分组的长度;L为考察区域长度;第x个空白分块组的绝对开始下标为i,绝对结束下标为j;f(z)和g(x,y)为权值函数.
M为目的节点已经收到视频块的总数;L为考察区域长度;Exist(k)函数为当前考察区域内视频块的存在状态,缺失时值为1,收到时值为0. 式(1)中,hweight(x,y)是对影响待接收视频分块因素的综合考量. 式(8)中,随机集中度P是评价RSCS算法调度性能的一个重要的指标.
2.2 RSCS算法步骤每个节点建立一个视频块的布尔向量表ani={a1,a2,a3…ak…an},ak表示第k个视频块的存在状态. 2个节点建立通信链接后,交换各自向量表并作逻辑运算,以便得到待发送视频分块的序列.
RSCS调度算法具体步骤如下.
第1步 源节点将所携带的原始视频切割成为若干个能单独播放的视频块.
第2步 当节点ni和nj相遇,它们交换各自的存在向量ani和anj. 然后,节点ni对存在向量进行异或操作ani∧¬(anj). 通过这个异或运算,可得节点ni待发送的视频块的序列.
第3步 节点ni和节点nj交换数据的过程中,待发送视频块在节点间基于RSCS的选择方式进行传输,因此计算待发送块视频块序列的每一个块的集中紧缺度.
第4步 根据待发送的视频块的集中紧缺度,将待发送块序列进行排序,选择集中紧缺度最大的视频块发送给接收节点.
第5步 在一次交换之后,节点双方更新各自的存在向量ani←ani∨icj→i,anj←ani∨ici→j. 其中,ici→j为节点ni发送给节点nj的视频块的存在向量,icj→i为节点nj发送给节点ni的视频块的存在向量.
第6步 进入下一次通信链接并返回第2步.
3 实验与仿真笔者使用ONE仿真器展开验证,实验中所需的参数设置如表 1所示.
|
|
表 1 实验所需参数 |
为了评价随机集中度算法的优劣,笔者采用如下比较基准:顺序数据分发和随机数据分发作为比较对象. 为了验证算法的有效性,评价指标为随机集中度和视频块递交平均延迟.
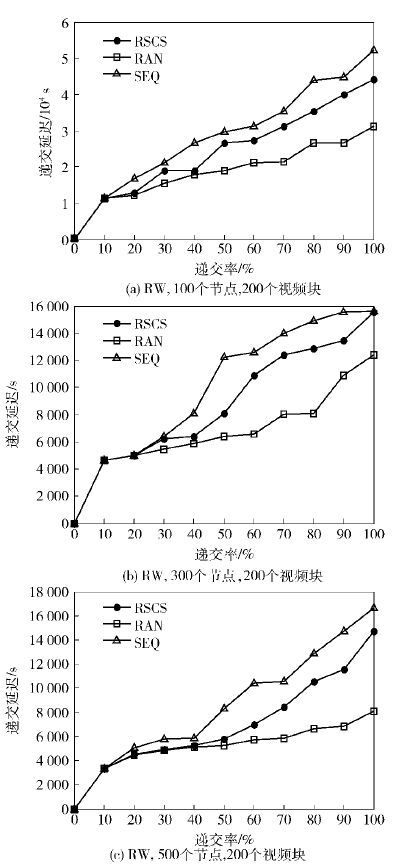
3.1 调度算法对递交时延的影响图 3所示为1 km×1 km场景下,视频块大小为100 kB情况下递交率和递交延迟的关系. 在图 3(a)和图 3(b)中,节点数目从100个到300个,同时递交时延呈现下降趋势,原因在于区域面积中节点数目增多,使节点间交换数据的频率大幅增加,有助于目的节点快速接收视频块. 在图 3(b)和图 3(c)中,从300个节点到500个节点,递交时延呈现了上升趋势,原因在于节点数目将近加倍,导致1 000 m×1 000 m的区域内,节点的密度大幅上升,使与每个节点建立连接的邻接节点的数目也有了显著的增加,导致节点交换数据的频率大幅增加. 因此,通过增加较小时间代价,却可换来视频分块按照应用的需求进行传输和分布.
|
图 3 递交率和递交延迟关系 |
RAN调度算法对待发送的视频块只做简单的转发并无过多的排序和优先级的计算,故而节点在移动中可快速完成数据的交换,因此邻居节点数目的增加使数据块能快速到达目的节点. SEQ调度算法中,每个节点要进行大量的排序,导致节点计算速度过慢,并引起周围的邻居节点数量增加,降低了节点与其他区域节点有效数据交互的机会,最终导致了递交时延的上升. 但RSCS算法中,由于采取了有目的、高效的分发视频分块的算法,使每个节点重复计算量增加的程度不高,因此邻居节点增加的程度不高,所以递交时延上升趋势不显著.
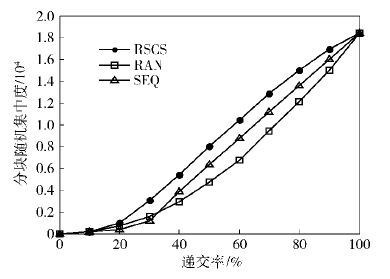
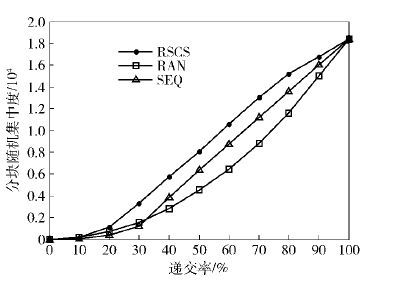
3.2 调度算法对分块集中度的影响图 4所示为区域面积1 km×1 km,100个节点,300个视频块的条件下递交率和分块随机集中度的关系. 图 5所示为区域面积300 m×300 m,100个节点,600个视频块条件下递交率和分块随机集中度的关系. 从图 4中30 MB视频和图 5中60 MB视频的传输过程可以发现,RSCS的视频块随机集中度最高,顺序传输SEQ的视频块随机集中度次之,随机分发RAN的视频块随机集中度最低. 这表明,RSCS使用户有较好的视频观赏体验,即在有限的时间内用户接收到的视频分块尽可能集中在某个时间区域,从而使用户能在短时间内快速获取视频的有效内容.
|
图 4 递交率和分块随机集中度关系(视频文件30 MB) |
|
图 5 递交率和分块随机集中度关系(视频文件60 MB) |
网络中节点的移动性造成机会网络处于割裂状态,使节点之间无法存在一条稳定的物理链路. 那么,网络中视频块的共享只能通过节点在运动过程中的相遇机会来完成数据的交换,从而实现整个网络对视频块的共享. 故而,中继节点中视频块的分布情况对于目的节点视频块的接收起着至关重要的作用. 图 4和图 5中,RAN调度算法使得所有节点中的视频块均处于离散状态,SEQ调度算法使节点中的视频块均按序号从小到大连续,RSCS调度算法中,所有的节点中的视频块均处于一种随机连续. 所有的节点采用RSCS的调度算法之后,目的节点中的视频块随机集中的强度明显优于中间节点不采用任何连续性算法的调度算法和使用了视频块按序连续的调度算法. 因此,中间节点也采用了RSCS的调度算法之后,增强了目的节点中视频块随机连续的程度.
从实际应用来看,RSCS调度算法面向紧急情况下的视频块的调度,机会网络中每一个节点不仅仅是用来转发数据的中继节点,这些节点也有着了解周围环境状态的实际需求. 因此,当所有的节点采用RSCS调度算法之后,短时间内全网用户都能对实际发生情况进行了解.
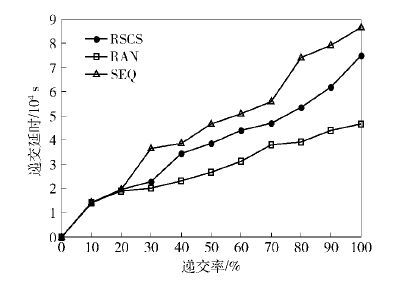
3.3 视频块的大小对调度策略的影响图 6所示为区域面积为1 km×1 km,200个节点,100个视频块情况下,视频块的大小对递交延时的影响. 图中视频块的大小为600 KB. 递交率相同时,SEQ的延迟最大,RAN最小,RSCS介于两者之间.
|
图 6 视频块的大小对递交延时的影响 |
提出一种基于分块紧缺程度的数据调度算法RSCS,该算法根据每个时隙所遇节点所接收到的数据块的分布情况,建立一个数据块紧缺程度的优先级函数,计算每一个分块的对应的分块紧缺程度,从而进行数据分发的操作. 根据丰富的实验表明,该算法平衡了数据分块的聚集性和数据分块的异质性,并适用于经典的路由协议Epidemic、Spray and Focus,能为恶劣机会网络环境下的视频大数据传输应用提供有效解决方案.
| [1] |
Pelusi L, Passarella A, Conti M. Opportunistic networking:data forwarding in disconnected mobile Ad hoc networks[J]. IEEE Communications Magazine , 2006, 44 (11) :134–141.
doi:10.1109/MCOM.2006.248176 ( 0) 0)
|
| [2] |
刘期烈, 胡春凤, 朱德利, 等. 机会网络节点兴趣社区检测及路由策略[J]. 北京邮电大学学报 , 2014, 37 (3)
:62–66.
Liu Qilie, Hu Chunfeng, Zhu Deli. Interest community detecting method and routing scheme in opportunistic networks[J]. Journal of Beijing University of Posts and Telecommunications , 2014, 37 (3) :62–66.
( 0) 0)
|
| [3] |
Belblidia N, Amorim M D D, Costa L H M K, et al. Part-whole dissemination of large multimedia contents in opportunistic networks[J]. Computer Communications , 2012, 35 (15) :1786–1797.
doi:10.1016/j.comcom.2012.03.006 ( 0) 0)
|
| [4] |
Li N, Das S K. A trust-based framework for data forwarding in opportunistic networks[J]. Ad Hoc Networks , 2013, 11 (4) :1497–1509.
doi:10.1016/j.adhoc.2011.01.018 ( 0) 0)
|
| [5] |
Ciobanu R I, Marin R C, Dobre C, et al. Interest-awareness in data dissemination for opportunistic networks[J]. Ad Hoc Networks , 2015, 25 :330–345.
doi:10.1016/j.adhoc.2014.07.004 ( 0) 0)
|
| [6] |
彭舰, 李梦诗, 刘唐, 等. 机会网络中基于节点社会性的数据转发策略[J]. 四川大学学报:工程科学版 , 2013, 45 (5)
:57–63.
Peng Jian, Li Mengshi, Liu Tang. Nodal sociality-based data forwarding for opportunistic networks[J]. Journal of Sichuan University:Engineering Science Edition , 2013, 45 (5) :57–63.
( 0) 0)
|
| [7] |
Mavromoustakis C X, Mastorakis G, Bourdena A, et al. Energy efficient resource sharing using a traffic-oriented routing scheme for cognitive radio networks[J]. IetNetworks , 2014, 3 (1) :54–63.
( 0) 0)
|


