为了有效处理三维列联表数据,采用模糊联合聚类算法的思想,提出一种基于信息瓶颈理论的模糊三维聚类算法(IBFTC).IBFTC算法为每个维度指定隶属度函数,可实现3个维度上的同时聚类,且在目标函数中引入信息瓶颈理论计算对象与簇之间的距离.采用MovieLens数据集对IBFTC算法进行多方面分析,结果表明,IBFTC算法可获得比现有模糊联合聚类算法更高的聚类准确率.
In order to group three-dimensional data, the thought of fuzzy co-clustering was adopted, and an information bottleneck based fuzzy tri-clustering algorithm, named IBFTC, was presented. The IBFTC specifies membership function for each dimension, simultaneously generates fuzzy clusters on three dimensions and adds information bottleneck theory into objective function for measuring distances between objects and clusters. Experiments on the MovieLens dataset evaluate the performances of IBFTC from several aspects. Experiment shows that IBFTC could achieve higher accuracy than conventional fuzzy co-clustering algorithms.
聚类算法有较长研究历史,迄今为止许多优秀算法[1-3]被陆续提出. 在针对文档-特征词二维列联表进行聚类时,传统聚类算法表现出两个主要特点:①硬聚类;②一维聚类. 事实上,文档对一个簇的隶属度应为区间[0,1]内的任意实数,故软聚类更符合数据的真实分布;另一方面,一维聚类因忽略了特征词间相关性可能对聚类准确性产生影响.
提出了一种基于信息瓶颈理论的模糊三维聚类算法(IBFTC,information bottleneck based fuzzy tri-clustering). 该算法对于三维列联表实现了三个维度的同时聚类,且采用信息瓶颈理论度量文档与簇质心间距,避免了从众多距离度量方法中随意选择造成的主观误差. 实验结果表明,IBFTC在实现三维聚类的同时,可有效提高聚类准确率.
1 信息瓶颈与模糊聚类信息瓶颈理论的基本思想来源于香农的信息率失真理论,其基本思想是给定待分类的样本空间X,特征空间Y的情况下,在样本中寻找一种分类方式,使其在对应分类情况下,样本与特征之间的共有信息损失最少. 基于信息瓶颈的聚类算法表现出优异的聚类效果[4].
模糊聚类将模糊理论加入聚类过程中,使得文档与簇之间原本由0和1二值表示的硬性隶属关系,变为由区间[0,1]内任意实数表示的软性隶属关系. 联合聚类技术可实现文档和特征词两个维度上的同时聚类,其优点可概括为:①维度约简;②簇的解释性增强;③聚类准确率提高. 模糊联合聚类在联合聚类技术基础上融入了模糊理论[5].
目前,针对三维列联表数据的聚类算法数量较少[6]. 已有算法虽实现了3个维度上的聚类,但难以实现软聚类,且部分算法通过融合联合聚类结果实现,无法实现3个维度上的同时聚类. 模糊三维聚类(FTC,fuzzy tri-clustering)算法[2]将分类多变元数据模糊聚类(FCCM,fuzzy clustering for categorical multivariate data)算法的思想从二维扩展到三维,实现了3个维度的同时聚类. 但FTC未考虑距离在目标函数中的重要性,因此在聚类质量上仍有提高空间.
2 基于信息瓶颈的模糊三维聚类 2.1 IBFTC算法IBFTC算法实现了对三维列联表3个维度的同时聚类,其主要思想包括两部分:①将FCCM和图像模糊联合聚类算法(FCCI,fuzzy coclustering algorithm for images)等模糊联合聚类处理二维列联表的思想进行扩展,以处理三维列联表,实现模糊三维聚类;②在模糊三维聚类过程中,强调距离关系在目标函数中的作用,且选择信息瓶颈理论用于距离计算.
IBFTC算法的目标函数如式(1)所示,其隶属度约束关系如式(2)~(4)所示.
| $\begin{align} & {{J}_{IBFTC}}=\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{i=1}{\overset{N}{\mathop{\sum }}}\,\underset{j=1}{\overset{K}{\mathop{\sum }}}\,\underset{k=1}{\overset{M}{\mathop{\sum }}}\,{{u}_{ci}}{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}+{{T}_{u}}\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{u}_{ci}}ln~{{u}_{ci}}+ \\ & {{T}_{v}}\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{j=1}{\overset{K}{\mathop{\sum }}}\,{{v}_{cj}}ln~{{v}_{cj}}+{{T}_{w}}\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{k=1}{\overset{M}{\mathop{\sum }}}\,{{w}_{ck}}ln~{{w}_{ck}} \\ \end{align}$ | (1) |
| $\sum\limits_{c=1}^{C}{{{u}_{ci}}=1,i=1,2,\ldots ,N}$ | (2) |
| $\sum\limits_{j=1}^{k}{{{u}_{ci}}=1,i=1,2,\ldots ,C}$ | (3) |
| $\sum\limits_{k=1}^{M}{{{u}_{ck}}=1,i=1,2,\ldots ,C}$ | (4) |
式(1)中,第1项指3个维度的聚合程度,uci,vcj和wck代表三个维度上的隶属度函数,Dcijk表示信息瓶颈距离,C、N、K和M分别表示簇数目、文档数目和另外两个维度的特征数目;第2、3和4项中,Tu,Tv和Tw控制三个维度的模糊程度.
在隶属度约束下求解目标函数的最小值,可采用拉格朗日乘数法,求解可得:
| ${{u}_{ci}}=\frac{exp\left\{ -\sum\limits_{j=1}^{k}{\sum\limits_{k=1}^{M}{{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}/{{T}_{u}}}} \right\}}{\sum\limits_{c=1}^{C}{\left\{ \sum\limits_{j=1}^{k}{\sum\limits_{k=1}^{M}{{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}/{{T}_{u}}}} \right\}}}$ | (5) |
| ${{v}_{cj}}=\frac{exp\left\{ -\sum\limits_{i=1}^{N}{\sum\limits_{k=1}^{M}{{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}/{{T}_{u}}}} \right\}}{\sum\limits_{j=1}^{k}{exp-\left\{ \sum\limits_{i=1}^{N}{\sum\limits_{k=1}^{M}{{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}/{{T}_{v}}}} \right\}}}$ | (6) |
| ${{w}_{ck}}=\frac{exp-\left\{ \sum\limits_{i=1}^{N}{\sum\limits_{j=1}^{K}{{{u}_{ci}}{{v}_{cj}}{{D}_{cijk}}/{{T}_{w}}}} \right\}}{\sum\limits_{k=1}^{M}{\exp -\sum\limits_{i=1}^{N}{\sum\limits_{j=1}^{K}{{{u}_{ci}}{{v}_{cj}}{{D}_{cijk}}/{{T}_{w}}}}}}$ | (7) |
对式(5)、(6)和(7)迭代更新,可得IBFTC的局部最优解. 其中,Dcijk使用信息瓶颈理论进行计算.
| ${{D}_{cijk}}=\frac{1}{N}{{x}_{ijk}}ln~({{x}_{ijk}}/{{t}_{jk}})+\frac{\left| c \right|}{N}{{p}_{cjk}}ln~({{p}_{cjk}}/{{t}_{jk}})$ | (8) |
式(8)中,
| ${{p}_{cjk}}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{u}_{ci}}{{x}_{ijk}}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{u}_{ci}}}$ | (9) |
其中xijk为三维矩阵的元素值.
2.2 收敛性证明可以证明,IBFTC算法会收敛到局部最优解.
引理1 根据式(5)迭代更新uci,不会增加式(1)中目标函数JIBFTC的值.
证明 把目标函数JIBFTC看成只关于uci的函数J(U).
| $J\left( U \right)=\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{i=1}{\overset{N}{\mathop{\sum }}}\,\underset{j=1}{\overset{K}{\mathop{\sum }}}\,\underset{k=1}{\overset{M}{\mathop{\sum }}}\,{{u}_{ci}}{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}+{{T}_{u}}\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{u}_{ci}}ln~{{u}_{ci}}+S~$ | (10) |
其中
同时,把vcj和wck看成常数,由拉格朗日乘子法,根据式(5)计算的u*值为J(U)的一个驻点. 为了证明u*为极小值点,只需证明海森矩阵Δ2J(u*)在u*处是正定矩阵.
| ${{\Delta }^{2}}J\left( u \right)=\left[ \begin{matrix} \frac{{{\partial }^{2}}J\left( u \right)}{\partial {{u}_{11}}\partial {{u}_{11}}} & \ldots & \frac{{{\partial }^{2}}J\left( u \right)}{\partial {{u}_{11}}\partial {{u}_{CN}}} \\ \vdots & \ddots & \vdots \\ \frac{{{\partial }^{2}}J\left( u \right)}{\partial {{u}_{CN}}\partial {{u}_{11}}} & \ldots & \frac{{{\partial }^{2}}J\left( u \right)}{\partial {{u}_{CN}}\partial {{u}_{CN}}} \\ \end{matrix} \right]=\left[ \begin{matrix} \frac{{{T}_{u}}}{{{u}_{11}}} & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & \frac{{{T}_{u}}}{{{u}_{CN}}} \\ \end{matrix} \right]$ | (11) |
对于u*,uci≥0 并且Tu也是总会被赋予一个正值,所以海森矩阵Δ2J(u*)是正定矩阵. 综上,u*是目标函数的驻点并且海森矩阵Δ2J(u*)为正定矩阵,由多元函数极值存在的充分必要条件知u*是目标函数JIBFTC的局部最小值点,所以根据式(5)迭代更新不会增加式(1)目标函数JIBFTC的值.
引理2 根据式(6)迭代更新vcj,不会增加式(1)中目标函数JIBFTC的值.
证明 与引理1 的证明方法相同.
引理3 根据式(7)迭代更新wck,不会增加式(1)中目标函数JIBFTC的值.
证明 与引理1的证明方法相同.
引理4 式(1)中的目标函数JIBFTC有界,即存在常数W,使得JIBFTC≥W.
证明 因为uci、vcj和wck的最小值为0,并且Dcijk≥0,所以式(1)中目标函数第1项可表示为
| $\underset{c=1}{\overset{C}{\mathop{\sum }}}\,\underset{i=1}{\overset{N}{\mathop{\sum }}}\,\underset{j=1}{\overset{K}{\mathop{\sum }}}\,\underset{k=1}{\overset{M}{\mathop{\sum }}}\,{{u}_{ci}}{{v}_{cj}}{{w}_{ck}}{{D}_{cijk}}\ge 0$ | (12) |
又式(1)中目标函数的第2项、第3项和第4项是熵公式,当uci=1/C,vcj=1/K并且wck=1/M时,达到函数最小值,即
JIBFTC≥TuNln(1/C)+TvCln(1/K)+TwCln(1/M)
Tu、N、C、Tv、Tw、K和M均为常数,所以当W=TuNln(1/C)+TvCln(1/K)+TwCln(1/M)时,JIBFTC≥W,即目标函数JIBFTC有界.
定理 引理1、引理2和引理3证明了IBFTC目标函数向局部最小值方向更新,引理4证明了IBFTC目标函数存在下限. 所以IBFTC目标函数JIBFTC必定收敛于满足约束条件式(5)~(7)的局部最小值.
3 实验 3.1 实验准备为了验证IBFTC算法的有效性,在MovieLens基础上进行了一系列实验,实验中选取模糊C均值聚类(FCM,fuzzy C-means)、FCCM、FCCI、鲁棒模糊联合聚类(RFCC,robust fuzzy coclustering)和FTC共5种算法进行对比. MovieLens包含了6 040位MovieLens用户对3 900部电影的共计1 000 209条评价. 基于MovieLens建立了2个数据子集分别记为DS1和DS2. 聚类质量的衡量标准选择F-Measure和Entropy.
3.2 实验结果与分析通过实验对IBFTC算法进行详细分析和验证,实验内容包括聚类准确率、参数影响和算法复杂度等方面.
1) 聚类准确率
为验证IBFTC算法的聚类准确率,在DS1和DS2两个数据集的基础上,将IBFTC与FCM、FCCM、RFCC、FCCI、FTC进行了对比. 实验结果如表 1所示.
|
|
表 1 用户维度上聚类准确率对比 |
在数据集DS1上,IBFTC算法的F-Measure值为0.661,Entropy值为0.251,相较于FCM、FCCM、RFCC、FCCI和FTC算法,F-Measure指标分别提高了5.6%、3.1%、3.1%、0.5%和1.4%,Entropy指标分别降低了0.8%、0.8%、0.8%、0和0.8%. 在数据集DS2上的实验结果中,IBFTC算法的F-Measure和Entropy指标值分别为0.319和0.742,F-Measure指标相比较对比算法分别提高了6.7%、1.2%、3.2%、2.2%和3.9%,Entropy指标分别降低了0.7%、0、0、0.3%和0.1%. 通过F-Measure和Entropy两个指标的对比可知,在DS1和DS2两个数据集上,IBFTC算法的聚类准确率在对比中表现最优. 除IBFTC外,FTC和FCCI算法的F-Measure和Entropy指标值在对比算法中表现较好.
FCCM、RFCC和FCCI均为模糊联合聚类算法,在用户维度上进行聚类的同时,在电影维度上也进行聚类;FTC和IBFTC为模糊三维聚类,不但在用户和电影两个维度进行聚类,而且在电影类型维度也生成了聚类结果. 表 2对比了IBFTC与FCCM、RFCC、FCCI、FTC算法在电影维度上的聚类质量. 在数据集DS1上,IBFTC算法的F-Measure值为0.695,Entropy值为0.326,两个指标均表明IBFTC算法的聚类准确率相较于FCCM、RFCC、FCCI和FTC有明显提高. 在数据集DS2上的实验结果中,IBFTC算法的F-Measure和Entropy指标值分别为0.524和0.467,表现优于对比算法. 同时可以看出,FTC和IBFTC算法的聚类质量明显优于其余模糊联合聚类算法,表明三维聚类算法因数据特征更丰富而容易获得更高的准确率.
|
|
表 2 电影维度上聚类准确率对比 |
通过本部分实验可知,IBFTC算法在DS1和DS2两个数据集上获得了比FCM、FCCM、RFCC、FCCI和FTC算法更高的聚类准确率;该算法和FCCM、RFCC、FCCI和FTC算法在电影维度上的聚类与用户维度同时进行,且IBFTC算法整体上仍然表现最优.
2) 参数影响
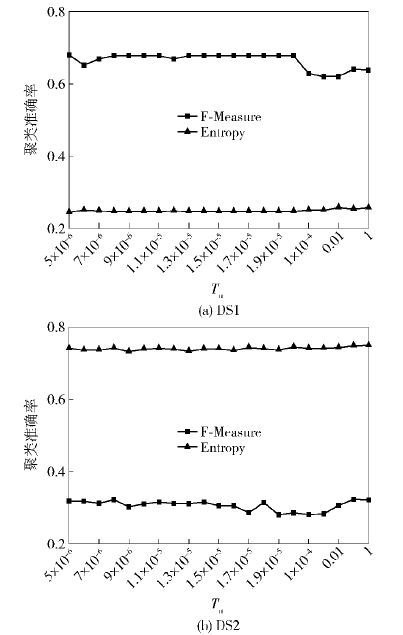
Tu是IBFTC算法中非常重要的一个参数,用于控制用户维度聚类中的模糊程度. 在实验过程中,指定Tu取值为10-5. 本部分实验通过赋予Tu不同取值多次聚类,考查IBFTC算法F-Measure和Entropy指标的变化情况,以分析该参数对聚类准确率的影响. 实验结果如图 1所示.
|
图 1 参数Tu对聚类准确率的影响 |
在区间[10-6,1]内,当参数Tu取值较小时,IBFTC算法在数据集DS1和DS2上的F-Measure和Entropy指标变化并不明显;当参数Tu取值较大时,F-Measure和Entropy指标的变化幅度略有增加,原因在于Tu值变大意味着用户与簇隶属关系的模糊程度增加,导致准确率略有降低. 总体而言,参数Tu对IBFTC算法准确率的影响较小.
3) 算法复杂度
算法的复杂度包括空间复杂度和时间复杂度,是衡量聚类算法质量的另一个重要指标.
对于FCCM、RFCC等模糊联合聚类算法,空间复杂度均为O(CN+CK),时间复杂度均为O(CNKτ),其中τ为迭代次数. FTC和IBFTC算法实现三维聚类,较模糊联合聚类算法增加了一个维度,其空间复杂度分别为O(CN+CK+CM)和O(CN+CKM),时间复杂度均为O(CNKMτ). 虽然在理论上IBFTC算法的时间复杂度略高,但通过实际的聚类时间对比(见表 3)可以发现,实际运行效率要高于理论分析. 在数据集DS1上的聚类时间甚至少于FCCI算法,在数据集DS2上的聚类时间虽然多于对比算法,但与FCCI相比,不足其时间的4倍,远低于理论上的M(在数据集DS2上,M=18)倍.
IBFTC算法实现了3个维度上的同时聚类,因此在时间复杂度上比模糊联合聚类算法有所增加. 但同样因为三维聚类,使得每个维度实现快速降维,导致IBFTC算法收敛较快,因此实际聚类效率要高于理论值.
|
|
表 3 算法运行时间对比 |
分析了现有的模糊聚类和模糊联合聚类算法,将模糊联合聚类算法在处理二维列联表时实现两个维度同时聚类的思想扩展到三维,并引入信息瓶颈理论计算对象与簇之间的距离,提出了一种基于信息瓶颈理论的模糊三维聚类算法IBFTC. 为验证IBFTC算法的有效性,在MovieLens数据集的基础上进行实验,从准确率、参数和时间复杂度等多个方面进行讨论分析. 实验结果表明,IBFTC算法可获得比现有模糊联合聚类算法更高的聚类准确率.
| [1] |
古恒, 陈钊, 王枞, 等. 双层聚类模型在日志数据分析中的应用[J]. 北京邮电大学学报 , 2015, 38 (1)
:63–66.
Gu Heng, Chen Zhao, Wang Cong, et al. The application of double layer clustering model on log data analysis[J]. Journal of Beijing University of Posts and Telecommunications , 2015, 38 (1) :63–66.
( 0) 0)
|
| [2] |
Liu Yongli, Yang Tengfei, Fu Lili. A partitioning based algorithm to fuzzy tri-cluster[J]. Mathematical Problems in Engineering , 2015 (12) :1–10.
( 0) 0)
|
| [3] |
孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报 , 2008, 19 (1)
:48–61.
doi:10.3724/SP.J.1001.2008.00048 Sun Jigui, Liu Jie, Zhao Lianyu. Clustering algorithms research[J]. Journal of Software , 2008, 19 (1) :48–61.
doi:10.3724/SP.J.1001.2008.00048 ( 0) 0)
|
| [4] |
Liu Yongli, Ouyang Yuanxin, Xiong Zhang. Incremental clustering using information bottleneck theory[J]. International Journal of Pattern Recognition and Artificial Intelligence , 2011, 25 (5) :695–712.
doi:10.1142/S0218001411008622 ( 0) 0)
|
| [5] |
Hanmandlu M, Verma O P, Susan S, et al. Color segmentation by fuzzy co-clustering of chrominance color features[J]. Neurocomputing , 2013, 120 (10) :235–249.
( 0) 0)
|
| [6] |
Mahiskar P S, Bhade A W, Chatur P N. An effective triclustering algorithm for mining real datasets:review paper[J]. International Journal of Computer Technology & Applications , 2012, 3 (1) :352–355.
( 0) 0)
|


