针对无线Mesh网络网关节点和网络链路承载的负载不均问题,择优选择网关节点,并设计链路权重,构建以网络加权吞吐量为优化目标的资源分配模型.在构建的资源分配模型下,提出一种基于Q学习和差分进化的联合功率控制与信道分配算法(QDJPCA).该算法通过获取功率控制的反馈结果,采用基于多重变异和自适应交叉因子的差分进化算法进行信道分配;针对每次迭代产生的信道分配结果,采用基于状态聚类和状态修正的Q学习算法实现功率控制.NS-3仿真结果表明,QDJPCA能够有效求解所提资源分配模型,在优先保证网关负载均衡和高负载链路吞吐量性能的基础上提升网络整体性能.
To solve the problem that the load which is carried by gateway node and that the network links in wireless Mesh network is imbalanced, a resource allocation model was constructed to optimize network weighted throughput by selecting the best gateway node and designing the weight on each link. A joint power control and channel assignment algorithm (QDJPCA) was proposed based on Q learning and differential evolution under the resource allocation model. In this algorithm, the channel assignment is achieved by obtaining the feedback results of power control, using the multiple mutations and adaptive crossover rate based differential evolution algorithm. In each iteration, to achieve power control, the Q learning algorithm based on state clustering and state correction is utilized on the channel assignment result. NS-3 simulation shows that the QDJPCA can not only effectively solve the proposed resource allocation model, but also improve the overall network performance through preferentially ensuring the gateway load balancing and throughput performance of heavy load link.
无线Mesh网络(WMN,wireless Mesh network)通过对网络链路进行合理的信道分配与功率控制可以显著降低网络干扰,从而提升网络性能. Kim等[1]借助于启发式算法实现面向吞吐量最大化的联合资源分配,但假设每条链路的信号干扰噪声比远大于1,与实际网络情况不符. Chaudhry等[2]提出的基于功率控制的拓扑控制和信道分配算法(e-TICA2,enhanced topology controlled interference aware channel assignment algorithm version 2)没有考虑网络干扰环境对链路功率选择的影响,同时没有从负载均衡的角度考虑网关选址问题. 伍春等[3]通过快速最优信道搜索结合用户聚类强化学习的方式实现多用户总收益的有效收敛,但其分层处理信道选择与功率控制问题,限制了网络性能的提升.
功率和信道的分配方案共同影响网络容量,因此考虑功率控制与信道分配的联合优化是非常必要的. 目前大多数联合优化方案都是将联合资源优化问题分解为两个子问题分别进行子问题的单次求解或按次序循环求解,没有充分考虑两个子问题之间的交互反馈求解. 笔者通过设计链路权重,构建面向网络加权吞吐量最大化的联合资源分配模型,提出一种基于Q学习和差分进化的联合功率控制与信道分配算法(QDJPCA,Q learning and differential evolution based joint power control and channel assignment algorithm),以实现功率和信道资源的有效分配. 仿真结果验证了QDJPCA在改善网络性能方面的有效性.
1 系统模型与问题描述 1.1 系统模型采用能够有效减少冗长链路和信道分配冲突的拓扑控制算法[2]生成WMN拓扑连接图G(N,E),其中N={1,2,…,nv}和E={1,2,…,ne}分别代表网络节点集合和网络连接边集合. 笔者从负载均衡的角度,在拓扑连接图上选取网络节点中各接口连接的节点数目最大值与最小值的差值最小的节点作为网关节点,选取网关节点Gselect的表达式为
| ${{G}_{select}}=min(max({{N}^{i}}_{k})-min({{N}^{j}}_{k})),\forall k\in N,i\ne j,\forall i,j\in {{\mu }_{k}}$ | (1) |
其中:Nki和Nkj分别为节点k的接口i和接口j连接的节点数目,μk为节点k的接口集合.
1.2 问题描述定义网络可配置的传输信道和功率等级集合分别为ø={1,2,…,nc}和Γ={1,2,…,np},其中nc和np分别为传输信道和功率等级数量.
令xmn代表链路(m,n)的1×nc维信道分配向量,若链路(m,n)分配了信道c,则xmn中元素xmnc=1,否则xmnc=0. 每条链路每次只能分配一条信道,故
| ${{x}_{mn}}{{1}^{T}}=1\left( \forall m,n\in N,m\ne n \right)$ | (2) |
其中1T为1×nc维单位向量的转置.
令ym表示节点m的1×nc维信道分配向量,若节点m的任意接口绑定了信道c,则ym中元素ymc=1,否则ymc=0. 任意节点m绑定的信道数受其接口数Im限制,故
| $\[{{y}_{m}}{{1}^{T}}\le {{\operatorname{I}}_{m}}\left( \forall m\in N \right)\]$ | (3) |
令zmn表示链路(m,n)的1×np维功率分配向量,若链路(m,n)分配了功率等级p,则zmn中元素zmnp=1,否则zmnp=0. 每条链路只能分配一个功率等级,故
| ${{z}_{mn}}{{\bar{1}}^{T}}=1\left( \forall m,n\in N,m\ne n \right)$ | (4) |
其中1T为1×np维单位向量的转置.
依据节点间的距离计算节点m到节点n的最小功率等级pmn[2]. 故链路(m,n)的功率等级p满足
| ${{p}_{mn}}\le p\le {{n}_{p}}\left( \forall m,n\in N,m\ne n,p\in \Gamma \right)$ | (5) |
令PN为背景噪声功率,γmnc,p为链路(m,n)分配信道c和功率等级p时的信号干扰噪声比,可表示为
| ${{\gamma }^{c,p}}_{mn}=\frac{{{P}^{t,c,p}}_{mn}{{g}_{mn}}{{x}^{c}}_{mn}{{z}^{p}}_{mn}}{{{P}_{N}}+\underset{\forall l\in N,l\ne m}{\mathop{\sum }}\,\underset{\forall h\in N,h\ne n}{\mathop{\sum }}\,\underset{p\in \Gamma }{\mathop{\sum }}\,{{P}^{t,c,p}}_{lh}{{g}_{ln}}{{x}^{c}}_{lh}{{z}^{p}}_{lh}},\forall m,n\in N,m\ne n,c\in \phi ,p\in \Gamma $ | (6) |
其中:Pmnt,c,p和Plht,c,p分别为链路(m,n)和干扰链路(l,h)的发射功率,gmn和gln分别为链路(m,n)的传播损耗和干扰链路(l,h)对链路(m,n)的同频干扰传播损耗,xmnc、zmnp和xlhc、zlhp分别为链路(m,n)和干扰链路(l,h)的资源分配向量xmn、zmn和xlh、zlh的组成元素.
故链路(m,n)的吞吐量Cmn可以表示为
| ${{C}_{mn}}=\underset{c\in \phi }{\mathop{\sum }}\,\underset{p\in \Gamma }{\mathop{\sum }}\,{{B}_{c}}lb(1+{{\gamma }^{c,p}}_{mn}),\forall m,n\in N,m\ne n$ | (7) |
其中Bc为信道c的带宽.
鉴于网络流量的网关汇聚特性,距离网关越近的链路,承载的负载越高,因此赋予的链路权重越大. 这里定义链路(m,n)的归一化链路权重wmn为
| ${{w}_{mn}}=\frac{{{L}_{mn}}}{\underset{u,v\in N,u\ne v}{\mathop{\sum }}\,{{L}_{uv}}}\left( \forall m,n\in N,m\ne n \right)$ | (8) |
其中:Lmn为通过链路(m,n)接入网关的节点数,
因此可以构建如下WMN加权吞吐量最大化的联合资源分配模型:
| $\underset{\phi ,\Gamma }{\mathop{maximize}}\,\underset{\forall m,n\in N,m\ne n}{\mathop{\sum }}\,{{w}_{mn}}{{C}_{mn}}$ | (9) |
Subject to: 式(2)~式(8)
式(2)~式(9)构建的联合资源分配模型是一个混合整数非线性规划问题,属于NP问题. 故将上述问题分解为功率控制与信道分配两个子问题,提出了QDJPCA.
2 联合功率控制与信道分配算法QDJPCA分为信道分配和功率控制两部分,其中信道分配借助于差分进化算法的全局求解能力,通过迭代寻优进行优化. 每次迭代过程中,每个个体需要经过功率控制的优化. 功率控制通过Q学习算法实现功率优化,并将优化结果反馈给信道分配,从而实现功率控制与信道分配的联合优化.
2.1 功率控制针对每次迭代产生的信道分配策略,采用基于状态聚类和状态修正的Q学习算法实现功率控制.
2.1.1 问题映射Q学习代理是网关节点,映射关系如下.
1) 状态空间S
S=(Smn,∀m,n∈N,m≠n),其中元素Smn为链路(m,n)的当前功率等级,即Smn∈{1,2,…,np}.
2) 动作空间A
A=(Amn,∀m,n∈N,m≠n),其中元素Amn∈{-1,0,1}为链路(m,n)当前功率等级的增量.
3) 回报函数
定义第t次学习中状态St+1和状态St的网络加权吞吐量之和的增量为回报函数,回报函数rt+1为
| ${{r}_{t+1}}=\underset{\forall m,n\in N,m\ne n}{\mathop{\sum }}\,{{w}_{mn}}{{C}^{{{S}_{t+1}}}}_{mn}-\underset{\forall m,n\in N,m\ne n}{\mathop{\sum }}\,{{w}_{mn}}{{C}^{{{S}_{t}}}}_{mn}$ | (10) |
其中:CmnSt+1为状态St+1下链路(m,n)的吞吐量,CmnSt为状态St下链路(m,n)的吞吐量.
2.1.2 状态聚类Q学习状态聚类Q学习算法主要通过动作选择、状态修正和Q值更新来实现功率控制,其步骤如下.
1) 初始化与学习空间构建. 初始化折扣因子η、学习速率α和贪婪搜索概率ε. 通过K均值聚类算法将网络节点划分成K类,并采取按节点类别执行动作的原则来实现状态聚类[3],按照2.1.1节的映射关系构建状态空间和动作空间.
2) 动作选择与执行. 针对当前状态St,依据ε贪婪策略选择动作At执行,动作执行结果S′t+1为
| $S{{\prime }_{t+1}}={{S}_{t}}+{{A}_{t}}(\forall {{S}_{t}}\in S,\forall {{A}_{t}}\in A)$ | (11) |
3) 状态修正. 判断S′t+1中链路功率等级是否满足限制条件式(5),如不满足则执行状态修正操作:
| ${{p}^{correct}}_{k}=\begin{matrix} {{p}_{k}}+{{p}^{rand}}_{k},{{p}_{{{k}_{mn}}}}<{{p}_{mn}} \\ {{p}_{k}}-{{p}^{rand}}_{k},\exists {{p}_{{{k}_{mn}}>{{n}_{p}}}} \\ \end{matrix}\text{ }$ | (12) |
其中:pkrand=rand(1,pΔk+1)为1~pΔk+1范围内的随机功率等级,pΔk为以k类节点为发送节点的链路的最小功率等级的最大值与np的差值,pk为以k类节点为发送节点的链路的功率等级,pkmn为以k类节点m为发送节点的链路(m,n)的功率等级.
4) 计算回报值与Q值更新. 状态修正后更新状态为St+1,依据式(10)计算回报值,更新Q值:
| ${{Q}_{t+1}}({{S}_{t}},{{A}_{t}})=\left( 1-\alpha \right){{Q}_{t}}({{S}_{t}},{{A}_{t}})+\alpha ({{r}_{t+1}}+\eta max{{A}_{t+1}}{{Q}_{t}}({{S}_{t+1}},{{A}_{t+1}}))$ | (13) |
其中:Qt+1(St,At)为更新后的Q值,Qt(St,At)为更新前的Q值,rt+1为回报函数值,maxAt+1Qt(St+1,At+1)为状态更新后采用不同动作能够得到的最优奖励值.
5) 算法终止条件判断. 如果达到了设定的学习次数则算法终止,否则返回步骤2),继续迭代执行.
2.2 信道分配通过获取Q学习功率优化结果,采用基于多重变异和自适应交叉因子的差分进化算法来优化信道分配策略,其执行步骤如下.
1) 个体编码
将网络链路的信道分配情况映射为种群中的个体,将每条链路所分配的信道映射为个体的基因. 为了增加问题解的直观性,方便依据网络链路端节点对网络链路进行索引,采用矩阵形式的基因结构[4]. 出于降低问题解的维数和提高算法收敛速度的考虑,个体DHi采用实数编码,编码方案为
| ${{D}^{i}}_{H}={{[{{d}_{mn}}]}_{\left| N \right|\times |N|}}\left( \forall m,n\in N,m\ne n \right)$ | (14) |
其中:|N|为网络节点数,i∈{1,2,…,Np}为个体编号,H∈{1,2,…,Hm}为进化代数,Hm为最大进化代数. 元素dmn随机取值如下:
| ${{d}_{mn}}=rand(1,2,\ldots ,{{n}_{c}})\left( \forall m,n\in N \right)$ | (15) |
若dmn=0,表示节点m和节点n之间无连通的链路,即不分配信道.
2) 初始化种群
执行Np-1次步骤1)为每条链路随机分配信道,产生Np-1个初始个体,将考虑同信道链路间干扰的信道分配结果[2]作为第Np个初始个体,通过对立学习机制[5]选择较优的Np个个体构成初始种群.
3) 多重变异
引入DE/best/1、DE/target-to-best/1和改进的DE/best/1/Either-Or变异算子[6],来增加变异个体VH+1i的多样性. 个体变异操作如下.
① DE/best/1:
| ${{V}^{i}}_{H+1}={{D}^{i}}_{best,H}+F({{D}^{i}}_{{{k}_{1}},H}-{{D}^{i}}_{{{k}_{2}},H})$ | (16) |
② DE/target-to-best/1:
| ${{V}^{i}}_{H+1}={{D}^{i}}_{H}+F({{D}^{i}}_{best,H}-{{D}^{i}}_{H})+F({{D}^{i}}_{{{k}_{1}},H}-{{D}^{i}}_{{{k}_{2}},H})$ | (17) |
③ DE/best/1/Either-Or:
| ${{V}^{i}}_{H+1}=\left\{ \begin{matrix} {{D}^{i}}_{best,H}+F({{D}^{i}}_{{{k}_{1}},H}-{{D}^{i}}_{{{k}_{2}},H})\text{ }若(rand[0,~1]f) \\ {{D}^{i}}_{best,H}+F\left( {{D}^{i}}_{{{k}_{1}},H}+{{D}^{i}}_{{{k}_{2}},H}-2{{D}^{i}}_{best,H} \right)其他 \\ \end{matrix} \right.$ | (18) |
其中:best,k1,k2∈{1,2,…,Np},且best≠k1≠k2≠i;pf=0.4;变异因子F=1;DHi为基准个体;Dk1i,H和Dk2i,H为随机个体;Dbest,Hi为当前种群中的最优个体.
为了保证变异个体在可行解的范围内,必须要对变异个体VH+1i进行越界处理. 即对节点产生冲突的接口重新分配信道,以满足式(2)和式(3)约束条件. 依据式(9)计算越界处理后变异个体的适应度函数值,选取其中最优的变异结果进行个体杂交操作.
4) 自适应杂交
通过将变异个体和当前个体进行杂交,按照一定概率得到候选个体UH+1i,个体杂交操作如下:
| ${{U}^{i}}_{H+1}=\text{ }\left\{ \begin{matrix} {{V}^{i}}_{H+1},若(rand[0,~1]\le R) \\ {{D}^{i}}_{H},其他 \\ \end{matrix} \right.$ | (19) |
其中交叉因子R=0.5+0.5×(1-H/Hm). 在算法初期R较大,能够增加变异个体的存活率,随着迭代的增加,R逐渐减小,有利于算法的有效收敛.
5) 个体选择
依据式(9)比较候选个体UH+1i和当前个体DHi的适应度函数值f(UH+1i)和f(DHi),选择保留的个体DH+1i如下:
| ${{D}^{i}}_{H+1}=\begin{matrix} {{D}^{i}}_{H},若(f({{U}^{i}}_{H+1}){{i}_{H}})) \\ {{U}^{i}}_{H+1},其他 \\ \end{matrix}\text{ }$ | (20) |
通过式(20)不断进行个体更新,经过种群的不断进化,最终将获得最优的信道分配策略.
2.3 算法时间复杂度QDJPCA的信道分配部分在Hm次进化中针对Np个个体需进行3HmNp次变异操作,故信道分配的时间复杂度为O(HmNpJ),其中J为网络链路数. 功率控制部分的Q学习过程仅利用当前状态和下一状态信息,每步的计算复杂度为O(1). 由于在信道分配的Hm次迭代中每个个体都需要经过Tm次Q学习的优化,故功率控制的时间复杂度为O(HmNpTm). 因此,QDJPCA的总时间复杂度为O(Hm2Np2TmJ),属于多项式级的时间复杂度,远低于集中式最优化算法的指数级时间复杂度.
3 性能评价与分析在NS-3仿真平台上进行算法性能仿真. 依次在400 m×400 m和750 m×750 m的区域中随机部署8个和20个网络节点,每个节点配置3个网络接口,网络信道数为3,节点最大发射功率为0.28 W,功率等级数为5,数据包接收门限为-64.3 dBm,负载感知门限为-78 dBm. 网络数据流为恒定比特率流,数据包长度为512 B. QDJPCA的参数为K=8,α=0.1,η=ε=0.9,Np=20,Hm=100.
3.1 性能仿真及分析在8个节点的网络场景下对比QDJPCA与遍历算法的近似程度,同时与以下两种算法比较收敛速度:① QDJPCA算法中信道分配部分采用Rahnamayan等[5]提出的改进差分进化的Q学习与对立差分进化算法(QODE,Q learning and opposition based differential evolution);② QDJPCA中信道分配部分采用Das等[6]阐述的基本差分进化的Q学习与基本差分进化算法(QDE,Q learning and differential evolution). 随后在20个节点的网络场景下与以下3种算法比较网络性能:① Chaudhry等[2]提出的e-TICA2;② Kim等[1]提出的贪婪式信道分配与固定功率控制算法(GC-FP,greedy channel assignment-fixed power control);③ 随机信道分配与固定功率控制算法(RC-FP,random channel assignment-fixed power control).
3.1.1 最优值近似程度与收敛速度仿真验证QDJPCA能够获得的最优值近似程度与收敛速度,仿真结果如图 1所示.
|
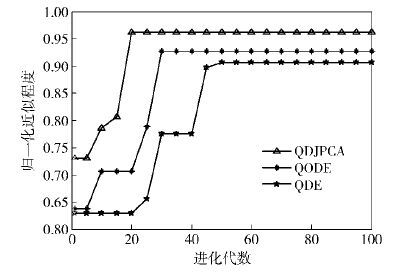
图 1 最优值近似程度与收敛速度 |
图 1仿真结果表明,QDJPCA经过20次迭代后平稳地收敛在最优值的96%,QODE和QDE算法分别经过30次和47次迭代稳定在最优值的92.8%和90.6%. 由此可见,QDJPCA具有较快的收敛速度,同时能够获得更高的最优值近似程度.
3.1.2 数据流个数对网络性能的影响固定节点发包速率,在不同数据流个数下对算法性能进行仿真,仿真结果如图 2所示.
|
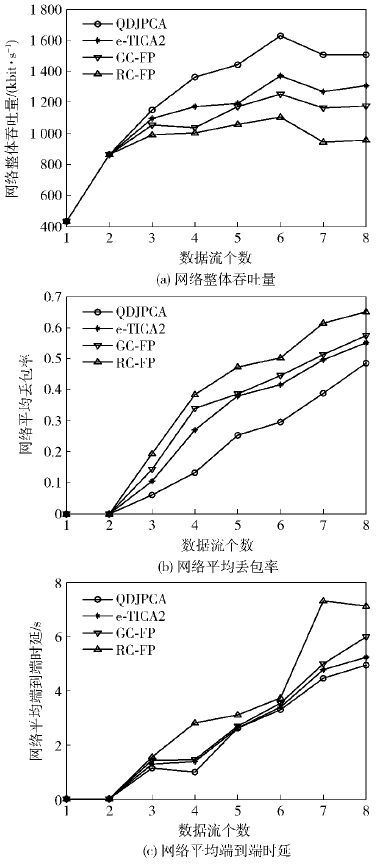
图 2 不同数据流数下的算法性能比较 |
图 2(a)表明随着网络数据流数的增加,网络整体吞吐量呈增长趋势. 当数据流数为4时,QDJPCA的网络整体吞吐量达到了1 362.6 kbit/s,分别比e-TICA2、GC-FP和RC-FP算法的网络整体吞吐量提高了16.2%、31.6%和35.8%. 由图 2(b)可以看出,QDJPCA在不同数据流数下均能获得网络平均丢包率性能的改善. 图 2(c)结果表明,QDJPCA的平均端到端时延始终低于其他算法的平均端到端时延. 图 2证明了QDJPCA能够在优先保证网关负载均衡和高负载链路吞吐量性能的基础上,通过功率与信道的联合分配实现网络性能的改善.
3.1.3 数据流发包速率对网络性能的影响固定数据流数为6,在不同发包速率下对算法性能进行仿真,仿真结果如图 3所示.
|
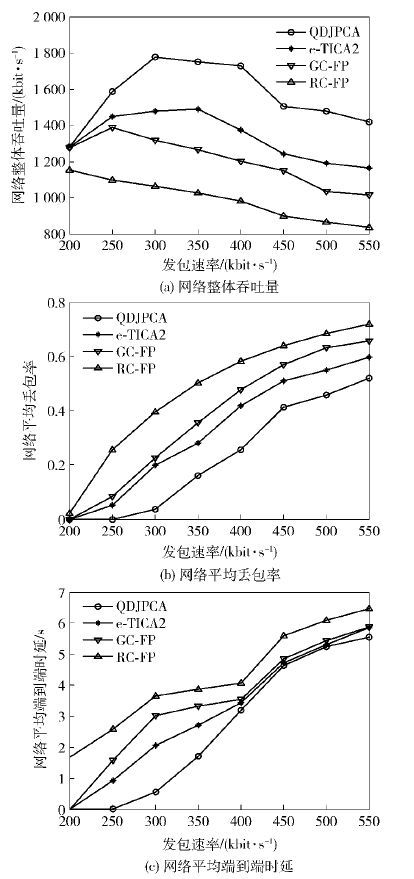
图 3 不同发包速率下的算法性能比较 |
图 3(a)表明QDJPCA的网络整体吞吐量始终高于其他算法的网络整体吞吐量. 当发包速率为350 kbit/s时,QDJPCA的网络整体吞吐量达到了1 750.8 kbit/s,分别比e-TICA2、GC-FP和RC-FP算法的网络整体吞吐量提高了17.4%、38.2%和70.8%. 由图 3(b)可知,QDJPCA的网络平均丢包率始终小于其他算法的网络平均丢包率. 图 3(c)结果表明,QDJPCA的平均端到端时延相比其他算法明显降低. 图 3同样证明了QDJPCA对网络性能的改善程度,能够获得更高的网络吞吐量和更低的网络时延与丢包率.
4 结束语通过择优选择网关节点并设计链路权重,构建了WMN面向吞吐量的联合资源分配模型,提出了QDJPCA. 该算法采用分层循环嵌套优化机制将功率控制融合到信道分配的求解过程中,其中信道分配结果通过基于多重变异和自适应交叉因子的差分进化算法进行求解,功率控制结果通过基于状态聚类和状态修正的Q学习算法进行求解. NS-3仿真结果表明,QDJPCA能够平稳地收敛到近似最优值,在优先保证网关负载均衡和高负载链路吞吐量性能基础上提升了网络整体性能.
| [1] |
Kim T S, Yang Yong, Hou J C, et al. Resource allocation for QoS support in wireless Mesh networks[J]. IEEE Transactions on Wireless Communications , 2013, 12 (5) :2046–2054.
doi:10.1109/TWC.2013.021213.120285 ( 0) 0)
|
| [2] |
Chaudhry A U, Ahmad N, Hafez R H M. Improving throughput and fairness by improved channel assignment using topology control based on power control for multi-radio multi-channel wireless Mesh networks[J]. EURASIP Journal on Wireless Communications and Networking , 2012, 155 .
( 0) 0)
|
| [3] |
伍春, 江虹, 易克初. 聚类多 Agent 强化学习认知无线电资源分配[J]. 北京邮电大学学报 , 2014, 37 (1)
:80–84.
Wu Chun, Jiang Hong, Yi Kechu. Cognitive radio resource allocation by clustering multi-agent enforcement learning[J]. Journal of Beijing University of Posts and Telecommunications , 2014, 37 (1) :80–84.
( 0) 0)
|
| [4] |
Yang Fengcheng, Chen Kuentai, Wang Mingtzong, et al. Mathematical modeling of multi-plant order allocation problem and solving by genetic algorithm with matrix representation[J]. The International Journal of Advanced Manufacturing Technology , 2010, 51 (9-12) :1251–1259.
doi:10.1007/s00170-010-2696-1 ( 0) 0)
|
| [5] |
Rahnamayan S, Tizhoosh H R, Salama M. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation , 2008, 12 (1) :64–79.
doi:10.1109/TEVC.2007.894200 ( 0) 0)
|
| [6] |
Das S, Suganthan P N. Differential evolution:a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation , 2011, 15 (1) :4–31.
doi:10.1109/TEVC.2010.2059031 ( 0) 0)
|


