2. 北京邮电大学 信息安全中心, 北京 100876
针对大规模无线射频识别(RFID)系统,提出一个安全双向认证协议.利用伪随机数生成器计算资源要求低的特性,使协议适用于存储空间小和计算能力不足的低成本标签环境中,采用平面直线斜率计算方法实现认证双方共享一对密钥,将认证的时间复杂度降低到O(1),引入时间戳来抵抗重放攻击,认证结束后进行身份更新防范标签位置追踪.形式化证明显示,该协议实现了标签与读写器的双向认证.仿真结果表明,与现有同类型主流协议相比,该协议认证效率提高了9%.
2. Information Security Center, Beijing University of Posts and Telecommunications, Beijing 100876, China
A mutual authentication protocol was proposed for large-scale radio frequency identification (RFID) system. Taking advantage of pseudo random number generator with little calculation resource requirement, the proposed protocol is suitable for low-cost tag environment with small storage space and low compute power. The slope calculation method of a line was adopted to realize both sides of authentication share a pair of keys and time complexity required to identify a tag can be reduced to O(1). The timestamp was introduced to resist replay attacks, and updates the identity to prevent location tracking. Formal proof shows that it realizes mutual authentication between the reader and the tag. Simulation shows that the proposed protocol can save 9% authentication time compared with some similar existing mainstream protocols.
无线射频识别(RFID,radio frequency identification)技术近年来发展迅速,但其安全问题也日趋显现,RFID安全认证协议成为保护标签隐私数据的主要研究方向之一[1]. 不难发现,现有协议大多数基于对称密钥方式[2],使得每次认证时,都需要读写器进行遍历计算. 为了解决这个问题,国内外学者提出了基于预计算[3]和基于二次剩余困难问题假设[4]等多种方案. 这些方案虽然提高了认证效率,但协议本身的安全性却无法保证[5].
笔者在Chou[6]的研究基础上,基于直线斜率计算方法和伪随机数生成器(PRNG,pseudo random number generator)算法,提出了一个新的轻量级RFID双向认证协议. 该协议在硬件和存储空间方面需求较低,一次认证运算能够在常数时间内完成,且可抵抗重放、身份假冒、标签位置追踪等多种攻击,实现了协议的安全性和认证效率的较好平衡.
1 RFID双向认证协议 1.1 平面直线斜率理论采用平面上直线来代表标签,并将该直线斜率作为标签的密钥值.
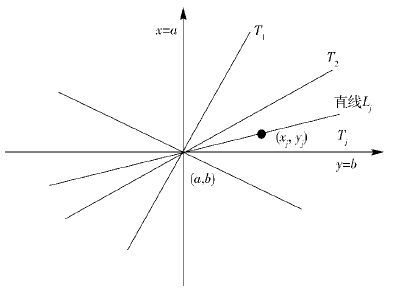
如图 1所示,随机选择点(a,b)作为读写器的秘密值,不失一般性,当所有直线通过原点时,有a=b=0. 一条直线Lj,斜率为kj,且通过点(a,b),它代表标签Tj . 这样直线Lj上的任何一个点(xj,yj),都可以存储在读写器中,作为标签Tj的一个身份证明. 同时,在大规模多标签环境中,读写器只需要存储一个点(a,b),然后它就可以和每个标签之间共享一个互不相同的密钥值kj.
|
图 1 斜率方法模型 |
表 1对文中需要用到的一些符号进行了描述.
|
|
表 1 符号描述 |
在初始化阶段,标签Tj被写入一个唯一动态身份DIDj、唯一密钥kj和当前时间戳Cold. 读写器Ri存储平面上一个点坐标(a,b)、它的身份值RIDi、关于标签的信息列表,这里只给出标签Tj的信息内容:{DIDoldj,DIDnewj,(xj,yj)}.
1.4 双向认证阶段假设读写器Ri与标签Tj之间相互认证,认证过程如下.
1) Ri生成一个时间戳Cnew,并根据RIDi计算Rrequest=PRNG(RIDi⊕Cnew).
2) Ri广播Cnew,Rrequest.
3) 收到认证请求之后,标签Tj首先验证Cnew是否大于Cold,且Rrequest是否等于R′request=PRNG(RIDi⊕Cnew). 如果成立,它生成一个随机数t,利用自己的密钥kj计算T=PRNG(t⊕DIDj⊕kj⊕Cnew).
4) Tj回复消息t,DIDj,T给Ri .
5) Ri根据DIDj查询到坐标(xj,yj),计算T′=PRNG(t⊕DIDj⊕Cnew⊕(xj-a)/(yj-b)). 若T′=T,继续进行计算:DIDoldj←DIDj、 DIDnewj←PRNG(Cnew⊕DIDj⊕(xj-a)/(yj-b))、R=PRNG(t⊕Cnew⊕DIDnewj).
6) Ri发送R给标签Tj .
7) 收到R之后,Tj根据Cnew,DIDj,kj计算获得 D′IDnewIDj和R′. 如果R′=R,Tj更新时间戳和身份值:Dj←PRNG(Cnew⊕DIDj⊕kj),Cold←Cnew.
2 基于GNY逻辑的形式化证明本节利用GNY(Gong,Needham,Yahalom)逻辑规则[7],对协议的安全性进行分析. 为了简化文章结构,证明过程中出现的逻辑规则,仅仅给出规则代号,具体规则内容可参见文献[7].
2.1 协议初始形式化根据1.4节双向认证协议交互流程,分别针对标签、读写器和协议目标的逻辑语言形式化表达如下.
1) 关于标签Tj的假设:Tj拥有身份值DIDj,伪随机生成函数PRNG(·),知道读写器的身份值RIDi;验证双方拥有相同的密钥值kj,所以Tj相信它与Ri共享kj;Tj生成t,所以它相信t是新鲜的.
标签的假设形式化表达:Tj∈DIDj,Tj∈RIDi,Tj∈PRNG(·),Tj∈kj,Tj∈t,Tj|≡
2) 关于读写器Ri的假设:Ri拥有身份值RIDi,伪随机生成函数PRNG(·),知晓读写器的身份值RIDi;验证双方拥有相同的密钥值kj,所以Ri相信它与Tj共享kj;Ri相信Cnew是新鲜的.
读写器的假设形式化表达:Ri∈RIDi,Ri∈PRNG(·),Ri|≡
3) 协议的目标:经过协议的安全运行,读写器Ri相信回复信息T是来自于目标标签Tj并且以前未被使用,也就是新鲜的;同样协议运行后,目标标签Tj相信认证信息R是来自于合法的读写器Ri并且以前未被使用,也就是新鲜的.
协议目标形式化表达为:
① Ri|≡Tj|~#(PRNG(t⊕DIDj⊕Cnew⊕kj));
② Tj|≡Ri|~#(PRNG(t⊕Cnew⊕D′IDnewj)).
2.2 协议目标形式化证明1.4节中的4)等价于:Ri收到t,DIDj,T语句,可GNY逻辑形式化为
| ${{R}_{i}}\triangleleft *(t,{{D}^{j}}_{ID},PRNG(t\oplus {{D}^{j}}_{ID}\oplus {{k}_{j}}\oplus {{C}_{new}}))$ |
也即
| ${{R}_{i}}\triangleleft *(t,{{D}^{j}}_{ID}){{R}_{i}}\triangleleft *PRNG(t\oplus {{D}^{j}}_{ID}\oplus {{k}_{j}}\oplus {{C}_{new}})$ | (1) |
由读写器前提假设可知: Ri∈(a,b),Ri∈(xj,yj).
根据GNY拥有规则P2可知:
| ${{R}_{i}}\in {{k}_{j}}=({{x}_{j}}-a)/(\text{ }{{y}_{j}}-b)$ | (2) |
根据读写器的假设可知:
| ${{R}_{i}}|\equiv {{R}_{j}}\overset{{{k}_{j}}}{\longleftrightarrow}{{T}_{i}}$ | (3) |
根据式(1)、接收原则TI、拥有原则P1可知:
| ${{R}_{i}}\in t,{{R}_{i}}\in {{D}^{j}}_{ID}={{D}^{j}}_{IDold}$ | (4) |
由拥有原则P2可知:
| ${{R}_{i}}\in (t\oplus {{D}^{j}}_{ID}\oplus {{k}_{j}}\oplus {{C}_{new}})$ | (5) |
由读写器假设Ri|≡φ(Cnew)和GNY可识别规则R1、R5可知:
| ${{R}_{i}}|\equiv \varphi (PRNG(t\oplus {{D}^{j}}_{ID}\oplus {{k}_{j}}\oplus {{C}_{new}}))$ | (6) |
由读写器假设Ri|≡#(Cnew)和GNY新鲜性规则F1可知:
| ${{R}_{i}}|\equiv \#(PRNG(t\oplus {{D}^{j}}_{ID}\oplus {{k}_{j}}\oplus {{C}_{new}}))$ | (7) |
由式(1)、式(2)、式(3)、式(5)、式(6)和消息解析规则I1可知:
| ${{R}_{i}}|\equiv {{T}_{j}}|\tilde{\ }\varphi (PRNG(t\oplus D{{\prime }_{ID}}\oplus {{C}_{new}}\oplus {{k}_{j}}))$ | (8) |
由式(7)和式(8)可知:
| ${{R}_{i}}|\equiv {{T}_{j}}|\tilde{\ }\#(PRNG(\oplus D{{\prime }_{ID}}\oplus {{C}_{new}}\oplus {{k}_{j}}))$ | (9) |
至此目标①得证.
类似于目标①的证明过程,应用GNY逻辑规则I1可以证明:
Tj|≡Ri|~φ(PRNG(t⊕Cnew⊕D′IDnewj))
根据前提假设Rj|≡#(t),应用GNY逻辑规则F1可以证明Tj|≡#(PRNG(t⊕Cnew⊕D′IDnewj)).
所以目标② Tj|≡Ri|~#(PRNG(t⊕Cnew⊕D′ IDnewIDj))成立. 其中D′IDnewj=PRNG(Cnew⊕Dj⊕kj).
3 协议安全和效率分析 3.1 协议安全性分析为了进一步证明协议的安全性,本节从窃听、冒充欺骗、重放、追踪和同步化攻击5个方面来进行分析,具体内容如下.
1) 抗窃听攻击:由于无线信道的不安全,对于所提协议,攻击者A可以通过窃听获取本次会话全部传输消息:Cnew,Rrequest,t,DIDj,T,R. 其中Cnew是随机值,DIDj代表标签的身份,如果本次认证成功,下次标签将更新身份值;如果认证失败,在A不知道读写器身份值RIDi的情况下,标签是不会响应的. PRNG(·)是安全单向函数,A通过Rrequest,T,R不能获得比随机数更多的信息. 所以,对于攻击者A来说,通过公开信道获取的信息,对发起攻击没有任何帮助.
2) 抗冒充攻击:所提出协议的目的是实现双向认证,其中所依赖的是读写器与标签之前共享密钥值kj的机密性,以及伪随机生成器PRNG(·)的强安全性. 如果相信对方身份的合法性,需要Cnew,Rrequest,T,R能通过验证. 本协议中,公开发送消息之间逻辑关系紧密,任何改动将会导致验证失败. 所以,本协议可以抵抗冒充攻击.
3) 抗重放攻击:为了抵抗重放攻击,本协议采用时间戳Cnew的方式. 由于每次时间信息的不同,重放之前的信息,将会无法通过时间戳和消息完整性的验证. 所以,本协议可以抵抗重放攻击.
4) 抗标签追踪攻击:追踪攻击的目的是获取某个标签的特征信息,确定不同的认证消息是来源于同一个标签. 在本协议中,攻击者希望可以依据某些特征信息将Tj从众多标签中识别出来. 有两种攻击途径可用来获取特征信息:①窃听Ri和Tj之间的所有通信;②利用窃听到的信息,对Tj实施重放攻击. 对于前者,由于标签引入了随机值,使得每次回复值也不同,同样每次认证成功之后DIDj值会更新,利用公开值获取标签特征是不可能的. 后者也即是重放攻击,本节第3)部分已经证明协议可以抵抗重放攻击. 所以,本协议可以抵抗标签追踪攻击.
5) 抗同步化攻击:攻击者A可以通过篡改、阻断等方式发动同步化攻击,使得协议不能完整运行,对于需要秘密值更新的协议机制而言,会导致认证双方分享值的不对称,引起后续所有认证的失败. 在本协议运行中,消息Cnew,Rrequest和消息t,DIDj,T识别失败,认证双方都未对DIDj值进行更新;消息R认证失败,只有读写器方进行了DIDj值更新,但其存储了(DIDoldj,DIDnewj)值,可确保双方共享信息的同步性. 所以,本协议可以抵抗同步化攻击.
3.2 协议硬件需求分析本节采用与现有协议相比较的方式,对新提出协议的硬件需求进行分析. 由于读写器的硬件配置较高,不依赖于算法的复杂度,所以本节只对标签的硬件需求进行分析.
如表 2所示,文献[3]基于Hash算法的安全性,文献[4]和文献[5]采用Hash算法和二次剩余算法组合的方式,它们至少需要8K门电路来实现协议运算. 然而,低成本的RFID标签只能够提供不超过3K门电路来用于安全保障,所以文献[3-5]提出的协议不适用于低成本标签环境中. 笔者提出的协议基于PRNG算法,只需要最多2K门电路即可满足其运算要求[8].
|
|
表 2 硬件需求分析 |
所提出的协议中,每个标签需要存储DIDj,Cold和256 bit的PRNG. 另外,标签还要存储每个被授权接入它的读写器信息,如kj,RIDi. 根据标签的记忆能力,可以选择恰当的密钥长度以达到理想的安全水平. 建议每个ID为128 bit(DIDj=128 bit,RIDi=128 bit)、密钥值为1 024 bit(kj=1 024 bit)、时间戳为256 bit,结果本协议标签的存储要求是(128+256+256)=640/8=80 B. 另外,需要存储一个授权读写器的空间是(1 024+128)=1 152/8=144 B.
轻量级被动式RFID标签的记忆空间是1 kbit~1 KB. 可见所提出的协议适用于轻量级RFID系统. 对于记忆空间达到8 KB的标签,最多可以存储56((8 192-80)/144≈56.3)个读写器信息. 所以,所提出的协议在确保安全的前提下,更加适用于低成本移动RFID环境中.
3.4 协议仿真分析所提出的协议在Intel 双核CPU、3.16 GHz、4 GB内存的PC上,采用NS-2模拟环境进行仿真. 由于所提出协议与文献[3, 5]都是固定时间认证,认证时间与标签的个数无关,且不需要服务器进行辅助运算,所以仿真对象只包括1个读写器和1个标签,统计完成一次认证协议运行的时间消耗. 为了统计的准确性,结果取100次仿真的平均值.
表 3总结文献[3, 5]和所提出协议的运算效率,其中EH、ES、EP和ER分别为一次Hash运算、二次剩余求解运算、PRNG运算和一次随机数生成运算的计算花费. 其中Hash函数采用长度为512 bit的SHA-1算法.
|
|
表 3 仿真分析 |
通过比较分析发现,文献[3]协议需要进行5轮交互、7次Hash运算,协议效率最低. 与其相比,所提出的协议在协议运算时间方面降低了近9%,具有更好的认证效率.
4 结束语安全和效率之间的平衡一直是低成本RFID系统身份识别机制需要解决的问题. 笔者基于PRNG,综合运用直线斜率计算方法、时间戳和身份值更新等手段,提出了一个新的双向认证协议,通过安全证明和效率分析发现,新协议认证时间复杂度为O(1),且可以满足RFID系统几乎所有必要的安全需求.
在实际应用中,标签-读写器间的认证效率除了受计算量、交互轮数等因素的影响之外,还受软硬件环境的限制. 所以下一步研究的重点在于,将提出协议应用于不同环境中进行验证,如航空器材管理、危险品运输等.
| [1] |
周世杰, 张文清, 罗嘉庆. 射频识别隐私保护技术综述[J]. 软件学报 , 2015, 26 (4)
:960–976.
Zhou Shijie, Zhang Wenqing, Luo Jiaqing. Survey of privacy of radio frequency identification technology[J]. Journal of Software , 2015, 26 (4) :960–976.
( 0) 0)
|
| [2] |
李晖, 夏伟, 邓冠阳, 等. PUF-HB#:轻量级RFID双向认证协议[J]. 北京邮电大学学报 , 2013, 36 (6)
:13–17.
Li Hui, Xia Wei, Deng Guanyang, et al. PUF-HB#:a lightweight RFID mutual authentication protocol[J]. Journal of Beijing University of Posts and Telecommunications , 2013, 36 (6) :13–17.
( 0) 0)
|
| [3] |
Alomair B, Clark A, Cuellar J, et al. Scalable RFID systems:a privacy-preserving protocol with constant-time identification[J]. IEEE Transactions on Parallel and Distributed Systems , 2012, 23 (8) :1536–1550.
doi:10.1109/TPDS.2011.290 ( 0) 0)
|
| [4] |
Chen Yalin, Chou Juesam, Sun Hungmin. A novel mutual authentication scheme based on quadratic residues for RFID systems[J]. Computer Networks , 2003, 52 (12) :2373–2380.
( 0) 0)
|
| [5] |
Yeh T C, Wu Chienhung, Tseng Y M. Improvement of the RFID authentication scheme based on quadratic residues[J]. Computer Communications , 2011, 34 (3) :337–341.
doi:10.1016/j.comcom.2010.05.011 ( 0) 0)
|
| [6] |
Chou Juesam. A constant-time identifying large-scale RFID tags using lines on a plane[J]. Transactions on emerging telecommunications technologies , 2014, 25 (11) :1083.
doi:10.1002/ett.v25.11 ( 0) 0)
|
| [7] |
Gong Li, Needham R, Yahalom R. Reasoning about belief in cryptographic protocols[C]//Proceedings of the 1990 IEEE Symposium on Research in Security and Privacy. Oakland, California:[s. n.], 1990:234-248.
( 0) 0)
|
| [8] |
Sundaresan S, Doss R, Zhou Wanlei, et al. Secure ownership transfer for multi-tag multi-owner passive RFID environment with individual-owner-privacy[J]. Computer Communications , 2015, 55 :112–124.
doi:10.1016/j.comcom.2014.08.015 ( 0) 0)
|


