2. 北京未来网络科技高精尖创新中心, 北京 100124
流表更新的无环一致性最优化方案的计算复杂度高,而反向、双向更新方案的计算复杂度低,依赖链长度难以得到有效的优化,为此提出了基于多向搜索的流表更新一致性方案.引入逻辑证明验证了该方案具有无环一致性.仿真结果显示,该方案具有接近最优化方案的依赖链长度,并且计算复杂度得到了显著优化.
2. Beijing Advanced Innovation Center for Future Internet Technology, Beijing 100124, China
The flow table updating with loop-free consistence is one of the most important issues in software defined networking (SDN), in which, the optimal scheme has high computing complexity, while the single/double directional updating schemes have low computing complexity, however, the length of dependency chain is difficult to be optimized. The article presents a consistent flow update scheme based on multi-directional searching. The scheme was proved loop-free consistent. Simulation shows that the scheme shortens the length of dependency chain, closes to the optimal scheme and effectively reduces the working load on controller.
与传统网络的分布式策略不同,软件定义网络(SDN,software defined networking)通过将控制平面集中到远端的一个逻辑控制器上,实现了数据平面和控制平面的解耦[1-2]. 现有的基于OpenFlow协议的SDN允许控制器安装规则,每个规则指定一个包头部位匹配,匹配包的行为模式有丢弃、转发、转移到控制器、优先级和超时等. 这种模式提高了网络的灵活性和可扩展性[3-4],并且使网络的管理更加便捷.
在网络的运行过程中,网络状态的变化时常发生,如路由切换、流量均衡、网络设备维护等. 在传统网络中,为了实现实时更新,防止瞬态异常,研究人员提出了许多扩展协议和操作实践,大大提高了网络系统的复杂度. 在SDN中,这些网络状态的变化,需要以更新交换机中流表项的方式,来实现对数据包的不同处理. 当SDN的流表更新时,需要在多个交换机上用新的流表项替换旧的流表项,如果不采用一定的方法,很可能出现同一个网络中同时存在新旧两套规则,使得数据传输出现错误,并且网络规模越大,出现问题的可能性越高. SDN控制器如何快速侦测到网络的不一致并快速解决这类问题,或者在更新流表时按照指定的规则避免不一致性问题的出现,是SDN领域的主要研究方向之一,对SDN的维护和扩展具有重要意义.
1 SDN流表更新一致性问题 1.1 一致性问题基本概念SDN中最为成熟的南向接口协议是开放网络基金会倡导的OpenFlow协议,目前已经成为SDN的主流南向接口协议之一[5]. OpenFlow流表更新的一致性问题[6]是:当网络状态发生变化时,部分OF交换机要由旧规则更新至新规则,在更新的过程中,由于SDN数据平面分布式的特性,控制器和交换机之间存在时延,各个交换机的更新顺序不确定,可能导致数据包在传输过程中同时按照旧规则和新规则处理,使传输逻辑发生暂时的混乱,如产生环路、拥塞等,因此控制器需要在更新时采取一定的策略,使流经交换机的数据包只按照旧规则或新规则进行处理. Mahajan等[7]研究发现一致性属性要求的强弱与交换机之间依赖关系的强弱存在正相关关系,即一致性属性要求越高,各交换机更新时对其他交换机的依赖程度也越高. 笔者选择弱化一致性属性为最具代表性的无环,即在更新过程的每一个状态下,任意多个交换机之间不允许产生环路.
1.2 无环条件下流表更新方案目前针对无环条件下的流表更新问题已有若干方案,为方便理解,给出如下定义. 父节点:一个节点Nc为Np的一个子节点,即Np为Nc的父节点,当且仅当对Nc存在指向Np新规则. 依赖关系:为避免环路,一个节点Na可以更新到新规则,当且仅当节点Nb完成更新,即节点Na依赖于节点Nb. 依赖关系树即流表更新过程中形成的复杂依赖关系,按照依赖关系树从根节点开始更新其孩子节点即可避免环路. 依赖链长度即形成的更新依赖关系树中最长的依赖链的长度. Mahajan等[7]提出的反向更新方案,核心思想可以从依赖关系树的角度来理解,即一个节点可以安全地更新到新规则,当且仅当其父节点的新规则已经更新. Fu等[8]提出的双向更新方案,核心思想是:寻找满足在当前更新状态下其子节点都已至新规则,或者在最终状态下其所有父节点都已更新至新规则,这两个条件的节点依次更新,即双向更新方案. 最优化方案[7]引入依赖森林的概念,依赖森林方案使用一种遍历式的寻找依赖关系信息的方法,依靠找到的所有依赖信息,在保证无环的情况下,让尽可能多的节点开始更新,因而获得最短依赖链长度. 最优化方案有最短的更新依赖链长度,但算法复杂度高.
综上,已有研究方案中,最优化方案有最短的更新依赖链长度,但计算复杂度高;反向更新方案和双向更新方案存在依赖链长度长、更新时延大等缺点. 笔者提出基于多向搜索的流表更新一致性方案,通过遍历原始图寻找所有可以更新的点进行更新分段,形成分段多向搜索的局面,增加可以同时更新的节点,有效缩短依赖链长度,减小更新时延.
2 基于多向搜索的流表更新一致性方案 2.1 方案描述首先定义,当一个节点Na在转发规则中通过节点Nb到达终点时,Na为Nb的父节点,Nb为Na的子节点. 同时定义,当节点Na必须在节点Nb更新完成之后才能更新时,称节点Na依赖于节点Nb,此时依赖链长度为1. 状态图T表示由所有交换机的转发规则构成的网络图,各个交换机由初始状态Ti经过多步到达最终状态Tf. 当某一节点Na满足以下条件之一时,更新其规则(删除旧规则,增添新规则)不会产生环路.
条件1:在当前更新状态Tt下,节点Na为根节点(无父节点),或其所有的父节点都已更新至新规则.
条件2:在最终状态Tf下,节点Na直接指向目的节点,或其在状态Tf下的子节点都已更新至新规则.
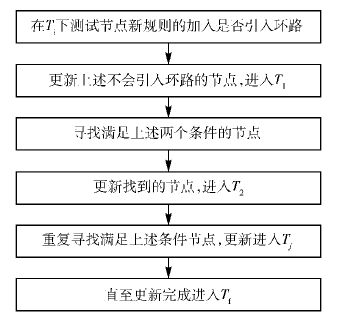
基于以上两点,更新方案算法流程描述如图 1所示.
|
图 1 基于多向搜索的流表更新一致性方案 |
1) 在初始状态Ti下,依次测试每个节点新规则的加入是否会引入环路. 如果没有引入环路,则该节点加入可更新的第1层节点;如果引入环路,则状态不变.
2) 同时更新(不分先后)第1层节点的规则(删除旧规则,增加新规则),当控制器收到第1层节点全部更新完成的确认信息后,状态图由Ti进入T1.
3) 假设第1层某个交换机出现故障,控制器在计时器到达某一指定值后仍未收到确认信息,则更新所有已收到确认信息的交换机的状态,进入状态T1.
4) 在状态T1下,寻找所有满足上述已证明的无环更新的条件1或者条件2的节点,加入可以更新的第2层节点.
5) 重复上述步骤2)~4),直到所有节点都已更新至新规则.
2.2 方案无环证明下面证明基于多向搜索的流表更新一致性方案保证更新过程中无环:首先是上述2个更新条件无环的证明,考虑第1种情况,在当前更新状态Tt下,节点Na为根节点(无父节点),或其所有的父节点都已至新规则,更新其规则,不会产生环路. 反证如下:假设在当前状态Tt下有一个未更新的节点Na,其所有的父节点都已更新至新规则,如果更新Na至新规则产生了环路Na→N0→N1→…→Nn→Na,显然有N0 ,N1,…,Nn在状态Tt下为Na的父节点,根据条件,它们已经全部更新至新规则,因此环路中所有节点的规则都是新规则,与新规则中不会有环路的假设矛盾,所以更新Na至新规则不会引入环路.
第2种情况与第1种类似,在最终状态Tf下,节点Na直接指向目的节点,或其在状态Tf下的子节点都已更新至新规则,更新节点Na,不会产生环路. 同样可以用反证法证明:假设在最终状态Tf下,节点Na的所有子节点都已更新至新规则,此时更新Na至新规则产生了环路Na→N0→N1→…→Nn→Na,显然有N0 ,N1,…,Nn在状态Tf下为Na的子节点,根据条件,它们都已更新至新规则,即此时环路中的所有规则都是新规则,与假设新规则中无环路矛盾,故更新节点Na至新规则不会引入环路.
另外,由于满足条件1的节点更新规则不会对条件2中已满足要求的节点产生影响,条件2同理,所以满足两个条件的节点的更新顺序先后对结果并无影响. 其次,第1层节点的更新过程中,由于加入其新规则经过检验不会产生环路,删除旧规则显然也不会产生环路,所以更新第1层节点的过程无环. 其后的步骤相当于在上述已证明更新过程正确性的条件下进行的更新. 综合上述两点,整个更新过程中不会产生环路.
方案完备性证明:第1层节点的更新过程中显然成立. 在之后的过程中,假设在某一中间状态Tt下更新停止,即有部分节点更新至新规则,剩余部分节点仍为旧规则,而且不满足条件1和条件2. 此时删除已更新的节点及其转发规则,使状态图由Tt变为T′t,显然在未更新的节点中一定会产生根节点,否则旧规则中就会有环路,与假设矛盾. 这些新产生的根节点是满足条件1的,所以这些节点可以更新至新规则,更新不会停滞. 证毕.
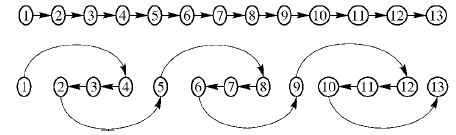
2.3 与相关研究比较为了分析基于多向搜索的流表更新一致性方案的特征,以图 2所示的网络拓扑为例,演示各个方案的更新过程及得到的结果,其中图上方表示的是旧的转发规则,下方表示的是新的转发规则,各个方案的更新过程简述如下.
|
图 2 无环方案示例 |
反向更新方案:按照新规则中从根节点到子节点的顺序,依次更新(13,10,11,12,9,6,7,8,5,2,3,4,1).
双向更新方案:寻找第1层可更新的节点,满足条件一的节点为1,满足条件二的节点为10,故第1层可更新节点为(1,10). 依次往下进行,每一层可更新的节点为(2,11)、(3,12)、(4,9)、(5,6)、(7)、(8),更新顺序是按照层次依次往下进行的.
最优化方案:依次加入每个节点的新规则,测试是否会产生环路,寻找到的依赖森林根节点有1、2、5、6、9、10,分别删除根节点的旧规则,寻找其子节点,找到的依赖树有2→3→4、6→7→8和10→11→12,故整个依赖森林为{(1)(2→3→4)(5)(6→7→8)(9)(10→11→12)},各个依赖树可以独立更新,不相互影响.
基于多向搜索的流表更新一致性方案:分别加入每个节点的新规则,测试是否新规则的加入会引入环路,找到的第1层节点有(1,2,5,6,9,10). 更新第1层中节点的规则(不分先后),在新的状态图中寻找满足条件1或者条件2的节点,有3、7、11,故第2层可更新的节点为(3,7,11). 依次往下进行,找到第3层可更新节点为(4,8,12),全部节点都已更新规则,更新完毕.
对更新一致性方案的评价指标一般包括以下几个方面:通用性,即考虑方案的适用范围;隔离性,即考虑是否可能对其他控制行为造成影响;更新时间,即实现更新过程的消耗时间;控制负载,即考虑给控制平面带来的额外负载. 下面将对基于多向搜索的流表更新一致性方案与反向、双向以及最优化方案进行比较分析.
1) 通用性:各个方案均是基于无环条件下的流表更新一致性方案,适用范围一致.
2) 隔离性:各个方案隔离性基本一致.
3) 更新时间:依赖链越长,时延越长. 对于有依赖关系的节点,为保证无环,只能等待其父节点更新完成后才能更新,父节点的更新延时直接影响子节点的更新完成时间,所以依赖链长度越长,更新时延越长. 反向更新方案,方案简单,实际网络中比较常用,每次更新一个节点,依赖链长度最长,更新时间最长;双向更新方案中,对于单一子节点的树形结构,每次寻找到的满足条件1或条件2的节点只有两个或者更少,因此这种情况下依赖链长度会较长,更新时间较长;基于多向搜索的流表更新一致性方案,首先通过遍历原始图寻找所有可以更新的点进行更新,形成分段多向搜索的局面,增加之后可以同时更新的节点,相对反向、双向更新方案扩展到多向更新,有效降低依赖链长度,更新时间短,与最优化方案基本一致.
4) 算法复杂度:在算法复杂度即控制器负载方面,假设4种方案全部使用邻接矩阵表示各个更新状态的状态图Tn. 反向更新方案中判断满足条件的算法时间复杂度为O(n),每一次更新完成后需要再次进行判断,所需判断次数的数量级为O(n2),因此总的时间复杂度为O(n3);双向更新方案中判断一个节点是否满足条件1或条件2的算法时间复杂度为O(n),每一层更新完成后需要再次进行判断,所需判断次数的数量级为O(n2),因此总的时间复杂度为O(n3);多向更新方案中第1步对所有节点判断加入其新规则是否会引入环路,时间复杂度为O(n2),后续步骤与双向更新方案的时间复杂度相同,因此总的时间复杂度为O(n3);最优化方案对每个状态为old的节点都要进行加入新规则是否有环路的判断,假设判断无环采用的是深度优先搜索算法,其时间复杂度为O(n2),每当一个节点由limbo状态更新至new状态就要对所有old节点进行检测,检测次数的数量级为O(n2),因此总的时间复杂度为O(n4),该方案算法复杂度最高.
反向、双向更新方案算法相对简单,时间复杂度低;多向更新方案由于只在第1步使用检查无环算法,算法复杂度相对于反向、双向方案虽然有所提高,但都保持在O(n3),低于最优化方案O(n4),整体算法仍较为简单,不会消耗太多控制器的计算资源.
综上,基于多向搜索的流表更新一致性方案相对反向、双向方案在控制器负载基本一致的情况下,降低了依赖链长度,缩短了更新时延;相对最优化方案,在更新时延基本一致的情况下,降低了计算复杂度.
3 仿真分析为了仿真4种无环更新方案在转发规则改变时的表现,以中国教育与科研计算机网CERNET的网络拓扑为例(来源:http://www.topology-zoo.org/files/Cernet.gml),涉及的主要省会、直辖市等骨干城市互联,用邻接矩阵抽象拓扑结构,通过最短路径算法获得转发规则,每次实验随机更改各个路径的权值来模拟链路状况的改变,各个链路的权值变化服从(0~1 000)均匀分布. 通过多次实验,对4种方案在多种情况下的依赖链长度进行对比分析,评价其性能.
4种无环更新方案的时间复杂度已在2.3节中进行了叙述,下面着重对4种方案在更新时间上的表现进行对比分析. 显然,当依赖链长度越长时,更新的时间也会越长,越有可能出现一个交换机发生问题导致其他交换机无法更新的情况. 而依赖链的长度与新旧转发规则交换机的重用率有关,即当新规则中使用越多旧规则中的交换机时,越有可能在更新时产生环路,依赖链的长度越长;当新规则使用越多新交换机时,更新过程中产生环路的概率越小,依赖链长度越短. 假设X代表网络拓扑中旧转发规则已使用的节点数,Y代表新转发规则可以选择的新的节点数,这样再加上原来旧转发路径的节点数,新转发规则总共可以选择的节点数即为(X+Y),则定义重用率R为
| $R=\frac{X}{\left( X+Y \right)}\times 100%$ | (1) |
基于以上两点,进行了以下数据测试. 首先,对于重用率R=25%、R=50%、R=75%情况下4种方案的表现进行测试,每组进行300次实验. 重用率的实现以R=50%为例,选定起始节点Na和目的节点Nb,以及一条在当前链路权值下的最短路径,假设此时这条旧路径上的交换机数目为X,额外选取可以生成从节点Na到达节点Nb新路径的X个新节点,加入新路径可以选择的节点集,这样新转发路径总共可以选择的节点数即为2X. 随机改变链路权值,可以得到新的转发规则,此时的重用率即为R=X/(2X)=50%. 选定额外节点后进行多次重复测试. 同时4种算法在同一测试中采用相同的节点和链路权值,并在各重用率下选取多个起点终点组合进行重复测试,结果如下.
1) R=25%
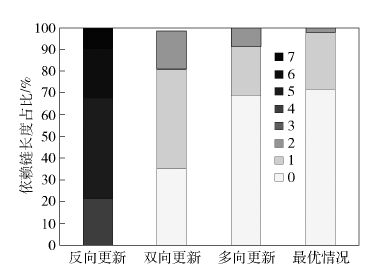
图 3中不同的灰度模块代表不同依赖链长度(0~7). 纵坐标代表各个灰度累加占总体的百分比,总体累加至100%,各个灰度模块的长度代表各个灰度(依赖链长度)的数目占总体的百分比. 当重用率较低时,反向更新性能较差,其他3种方案较短的依赖链长度(如0、1)占得比例较大,最优化方案短依赖链比例最高,3种方案之间的差距较小,相对反向、双向更新方案,多向更新方案中短依赖链长度比例明显有优势.
|
图 3 R=25%情况下依赖链长度 |
2) R=50%
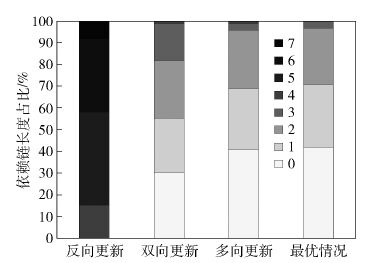
图 4中,相对R=25%的情况,双向更新方案的依赖链长度有明显增加,而多向更新方案的依赖链长度虽然也有增加,但是较短的依赖链仍然能占到70%,与最优情况基本一致.
|
图 4 R=50%情况下依赖链长度 |
3) R=75%
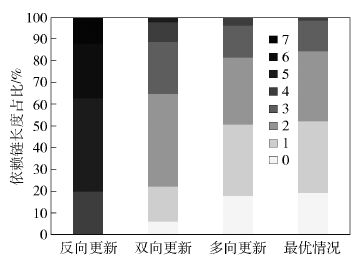
如图 5所示,当新旧规则使用的交换机重用率增加后,双向更新方案的依赖链长度继续增加,而多向更新方案的依赖链长度虽然也有增加,但是较短的依赖链仍然能占到50%,接近最优情况.
|
图 5 R=75%情况下依赖链长度 |
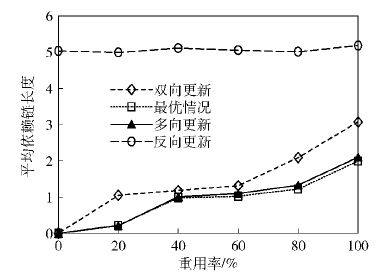
接着,对4种方案在不同重用率下的平均依赖链长度进行统计对比,如图 6所示.
|
图 6 不同重用率下的平均依赖链长度 |
反向更新方案只与新的转发规则相关,其依赖链长度为转发跳数减1,仿真中平均转发跳数为6跳左右,所以反向更新方案的平均依赖链长度保持在5上下波动. 双向和多向更新方案的依赖链长度与新旧转发规则都相关,平均依赖链长度都随着交换机重用率的增加而上升. 双向更新方案上升得较快,尤其当重用率较高时,其陡峭程度明显增加;多向更新方案的平均依赖链长度上升得较为平缓,其平均依赖链长度低于双向更新方案,结果逼近最优化方案.
综上,基于多向搜索的流表更新一致性方案相对于反向、双向方案有效降低了依赖链长度,减小了更新时延,提高了更新效率,方案结果逼近最优化方案.
4 结束语无环更新方案的依赖链长度和算法复杂度之间存在着折中关系. 反向、双向方案算法简单,时间复杂度低,但是一般情况下依赖链长度较长;多向更新方案首先通过遍历原始图寻找所有可以更新的点,形成分段多向搜索的局面,从单向、双向扩展到多向,增加之后可以同时更新的节点,有效降低了依赖链长度,减小了更新时延,更新结果逼近最优化方案,而且由于只在第1步使用检查无环的算法,算法复杂度相对于反向、双向方案虽然有所提高,但整体算法相对最优化方案仍较为简单,不会消耗太多控制器的计算资源. 在后续工作中,可以针对实际网络某个具体应用进行进一步优化.
| [1] |
McKeown, Ni ck, Tom Anderson, et al. OpenFlow:enabling innovation in campus networks[J]. ACM SIGCOMM Computer Communication Review , 2008, 38 (2) :69–74.
doi:10.1145/1355734 ( 0) 0)
|
| [2] |
Bianco, Andrea, Robert Birke, et al. Openflow switching:data plane performance[C]//Communication(ICC), 2010 IEEE International Conference on.[S. l.]:IEEE, 2010:1-5.
( 0) 0)
|
| [3] |
Farhady, Hamid, HyunYong Lee, et al. Software-defined networking:a survey[J]. Computer Networks , 2015 (8) :79–95.
( 0) 0)
|
| [4] |
Nunes, Bruno Astuto A, Marc Mendonca, et al. A survey of software-defined networking:past, present, and future of programmable networks[C]//IEEE Communications Surveys & Tutorials 16. 2014:1617-1634.
http://cn.bing.com/academic/profile?id=2125560635&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| [5] |
Sood, Manu. Software defined network-architectures. In Parallel, Distributed and Grid Computing (PDGC)[C]//2014 International Conference on, IEEE. 2014:451-456.
( 0) 0)
|
| [6] |
Tarjan, Robert. Depth-first search and linear graph algorithms[J]. SIAM Journal on Computing 1 , 1972 (2) :146–160.
( 0) 0)
|
| [7] |
Mahajan, Ratul, Roger Wattenhofer. On consistent updates in software defined networks[C]//Proceedings of the Twelfth ACM Workshop on Hot Topics in Networks. 2013.
http://cn.bing.com/academic/profile?id=2068384525&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| [8] |
Fu, Jing, Peter Sjodin, Gunnar Karlsson. Loop-free updates of forwarding tables[C]//IEEE Transactions on Network and Service Management 5. 2008(1):22-35.
http://cn.bing.com/academic/profile?id=2119521834&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|


