针对移动终端在蜂窝网络中的能耗过高问题,提出了一种基于时间序列的能量优化算法——平衡优化算法(BOA).该算法对移动终端在蜂窝网络中传输的数据块建立自回归滑动平均模型,通过预测下一个数据块的到达时间来动态调整尾巴时间,达到降低能耗的目的.实验结果及分析表明,BOA能达到93.86%的模型匹配率;相比于原标准下的Fixed-tail算法,能达到42.25%的能量优化效果,且用户使用移动终端时间越长,能量优化效果越好.
Aiming at the high energy consumption of mobile terminal under cellular networks, a new energy optimization algorithm balance optimization algorithm (BOA) based on time series is proposed to improve the energy efficiency of smartphones. The proposed algorithm builds the auto-regressive and moving average model for the data blocks in the cellular network, and dynamically adjusts the tail time to achieve the purpose of reducing the energy consumption by predicting the arrival time of the next block. Experiments show that BOA can achieve the average model matching rate up to 93.86%. Compared to traditional fixed-tail algorithm, the BOA enables reduce energy consumption by 42.25%,and analysis shows that the longer smartphones are used, the higher energy efficiency can be achieved.
降低尾巴时间所带来的能量浪费成为3G网络中移动终端能源优化的热点[1]. 一种方法是将时延要求不高的数据业务捆绑在一起,选择合适的时机进行发送来减少尾巴时间出现的次数,但不适用于时延要求很高的数据业务类型[2-3];另一种方法是根据网络负载和传输需求动态调整尾巴时间来降低能耗,但此类方法会增加用户时延[4]. 笔者提出了一种基于时间序列的能量优化算法——平衡优化算法(BOA,balance optimization algorithm),首先利用自回归滑动平均(ARMA,auto-regressive and moving average)模型对数据块的时间间隔(TAB,time of adjacent blocks)序列进行建模,预测下一个数据块的到达时间,然后根据预测值去除不必要的尾巴时间来降低能耗,并在下一个数据块到来之前提升3G接口至高能耗状态,提高用户的体验度.
1 能量状态及转换基于3G网络的终端接口包含3个能量状态[5]: 休眠(idle)、前向接入信道(FACH,forward access channel和专用信道(DCH,dedicated channel). 休眠状态为设备不与基站建立链路链接,基本上不消耗能量;DCH状态为设备与基站之间建立链路链接,能量消耗较快;FACH状态为数据传输完成以后,设备被分配一条共享的链路,仅支持低速率的数据传输,能耗较小. 当数据传输完成以后,设备接口会在DCH状态下维持T1的时间,若没有数据包的到来,转入FACH状态,并维持T2的时间,直到没有数据包到来,转入IDLE状态,此时T1与T2时间段内的能耗便是一种不必要的能量浪费.
2 BOA描述下面主要针对时延要求很高的数据业务类型(网页浏览和流媒体)进行研究.
2.1 TAB序列将数据块作为研究对象,定义数据块为一连串彼此时间间隔很小的数据包,定义数据块时间间隔序列TAB为相邻2个数据块之间的时间间隔形成的序列. 由于平稳时间序列的均值为0,而实际序列的均值是未知的,因此对TAB序列进行0均值化处理,并使用自相关系数法[6]对处理后的样本进行平稳性检验,若表现出明显的拖尾性,则证明该TAB序列是平稳的.
2.2 ARMA模型的建立因为提取的TAB序列是平稳的,所以可直接对其建立ARMA模型.
ARMA模型的一般形式为
| $\begin{align} & {{y}_{t}}=c+{{\varphi }_{1}}{{y}_{t-1}}+{{\varphi }_{2}}{{y}_{t-2}}+\ldots +{{\varphi }_{p}}{{y}_{t-p}}+{{\varepsilon }_{t}}+ \\ & {{\theta }_{1}}{{\varepsilon }_{t-1}}+{{\theta }_{2}}{{\varepsilon }_{t-2}}+\ldots +{{\theta }_{q}}{{\varepsilon }_{t-q}}~ \\ \end{align}$ | (1) |
其中:yt-1,yt-2,…,yt-p为平稳序列过去p个观察值,p为自回归阶数,q为滑动平均阶数,εt,εt-1,εt-2,…,εt-p为误差分量,Φ1,Φ2,…,Φp,θ1,θ2,…,θq为模型参数,c为常数.
2.2.1 混合准则法确定模型的阶数ARMA模型常用的定阶准则有[7]
1) 赤池信息准则(AIC,Akaike information criterion)
| ${{A}_{(p,q)}}=Nln~{{\sigma }^{2}}+2\left( p+q \right)$ | (2) |
2) 贝叶斯信息准则(BIC,Bayesian information criterion)
| ${{B}_{(p,q)}}=Nln~{{\sigma }^{2}}+\left( p+q \right)ln~N~$ | (3) |
其中:N为训练数据的个数;σ2为拟合后的残差方差;p为自回归阶数,q为滑动平均阶数,分别取AIC值和BIC值最小时的模型参数为最佳模型阶数. 笔者提出一种基于AIC和BIC准则的混合准则定阶法. 该方法将AIC和BIC准则相结合,克服了单个准则定阶时选择困难问题,同时能相互弥补对方的缺点,使模型的精确度更高.
TAB序列的训练数据可能会出现多个充分模型Mi (i=1,2,3,…),对于其中的每一个Mi,都有一组AIC(p,q)值和BIC(p,q)值与之相对应. 混合准则定阶法定义为
| $BCAB=min~\{{{\lambda }_{1}}{{A}_{(p,q)}}+{{\lambda }_{2}}{{B}_{(p,q)}}\}$ | (4) |
其中λ1和λ2为A(p,q)和B(p,q)被赋予的权重值,采用熵值法来确定权重λ1和λ2. 熵值法是一种比较客观的确定权重的方法,能避免层次分析等人为打分的主观性,也能避免变异系数法确定权重时误差较大的问题,客观性强. BCAB确定模型阶数的步骤如下.
1) 计算各充分模型相应的准则函数值,构成矩阵为
| $\left( \begin{array}{*{35}{l}} A({{M}_{1}}) & B({{M}_{1}}) \\ A({{M}_{2}}) & B({{M}_{2}}) \\ \vdots & \vdots \\ A({{M}_{n}}) & B({{M}_{n}}) \\ \end{array} \right)$ |
2) 将上述矩阵记为
| $\left( \begin{array}{*{35}{l}} {{X}_{(1,1)}} & {{X}_{(1,2)}} \\ {{X}_{(2,1)}} & {{X}_{(2,2)}} \\ \vdots & \vdots \\ {{X}_{(n,1)}} & {{X}_{(n,2)}} \\ \end{array} \right)$ |
其中:X(i,1)为A(Mi),X(i,2)为B(Mi)(i=1,2,3,…,n).
3) 对数据进行标准化,计算第i个充分模型第j个准则的特征比重为
| ${{P}_{(i,j)}}=\frac{{{x}_{(i,j)}}}{\sum\limits_{i=1}^{n}{{{x}_{(i,j)}}}},i=1,2,3\cdots ,N,j=1,2$ | (5) |
4) 第j项指标的熵值为
| ${{e}_{j}}=-k\sum\limits_{i=1}^{n}{{{p}_{(i,j)}}ln({{p}_{(i,j)}})}$ | (6) |
5) 计算指标差异系数为
| ${{g}_{j}}=1-{{e}_{j}}$ | (7) |
gj越大,表明越应该重视这项指标的作用.
6) 确定权数为
| ${{\lambda }_{j}}=\frac{{{g}_{j}}}{\sum\limits_{i=1}^{n}{{{g}_{j}}}},\text{ }j=1,2$ | (8) |
确定权重后,使得BCAB值最小的模型阶数p和q为最佳模型阶数.
2.2.2 自回归逼近法确定模型的参数笔者使用自回归逼近法来确定模型的参数. 首先为TAB序列建立AR模型,取自回归阶数的上界为
| ${{p}_{0}}=\left\lfloor \sqrt{N} \right\rfloor $ | (9) |
其中N为训练数据的个数. 采用BCAB混合定阶法先得到AR模型的阶数估计 Ap^G2 和自回归系数的估计(
| ${{\hat{\varepsilon }}_{t}}={{y}_{t}}-\sum\limits_{j=1}^{{\hat{p}}}{{{\varphi }_{j}}{{y}_{t}}-j}$ | (10) |
其中
| ${{y}_{t}}=\sum\limits_{j=1}^{p}{{{\phi }_{j}}yt-j+{{{\hat{\varepsilon }}}_{t}}+\sum\limits_{j=1}^{q}{{{{\hat{\varepsilon }}}_{t-j}}}}$ | (11) |
其中:t=l+1,l+2,…,N,l=max (
| $Q(p,q)={{\sum\limits_{t=l+1}^{N}{\left( {{y}_{t}}-\sum\limits_{j=1}^{p}{{{\phi }_{j}}{{y}_{t-j}}-\sum\limits_{j=1}^{q}{{{\theta }_{j}}{{{\hat{\varepsilon }}}_{t-j}}}} \right)}}^{2}}$ | (12) |
最小化,得到最小二乘估计(
| ${{\sigma }^{2}}=\frac{Q\left( p,q \right)}{N-l}$ | (13) |
为TAB序列建立好ARMA模型之后,便可对下一个时间间隔进行预测. 图 1为实测TAB序列值和为其建模后的预测值.

|
图 1 TAB序列的实际值和预测值 |
对TAB序列中的下一个序列值进行预测之后,便可对无线资源控制协议进行优化. 设下一个TAB序列的预测值为T,Promotion时延为Tpromotion:
1) 若Tpredict<Tpromotion,保留该设备的尾巴状态.
2) 若Tpredict>Tpromotion,则在当前数据包传输完成之后,立即将设备的3G数据接口转入IDLE状态(去尾操作). 并且为了不影响用户的体验度,提前Tpromotion时间将3G数据接口提升至FACH状态(时延操作).
3 算法验证 3.1 系统实现笔者选用搭载Android操作系统的GalaxyS5移动终端作为BOA实现的原型机. 为了消除智能手机制造商对BOA的影响,选用3GPP R8中规定的标准快速休眠机制来实现去尾操作[8]. 当预测的下一个数据包的到达时间超过Tpromotion时,移动终端通过控制信道发送一个SCRI,并伴随IE消息,网络接受IE消息触发电池转入IDLE状态. 当需要执行时延操作时,终端向特定的服务器发送一个UDP数据包,使得数据包到达时3G接口处于数据传输状态.
3.2 实验结果30名志愿者被平均分为A、B和C三组. 实验采用Agilent 34411A数字万用表来测量智能手机经过BOA优化后的能耗,与之相比的是Fixed-Tail算法,即原标准下拥有固定长度的尾巴时间. 实验1:首先每位志愿者提取10 min的TAB序列. 然后,A组、B组和C组先在Fixed-Tail算法下分别使用手机10 min、20 min和30 min,再在BOA下分别使用手机10 min、20 min和30 min,同时使用Aligent数字万用表测量这30名志愿者所使用智能手机的能耗.
1) 实验2:将TAB序列的提取时间延长到20 min.
2) 实验3:将TAB序列的提取时间延长到30 min.
由于篇幅所限,只列举实验1 A组的实验结果如表 1所示. 其中STAB、MMR、Fixed-tail、BOA和EOR分别代表TAB序列大小、模型匹配率、Fixed-tail算法的能耗(优化前能耗)、BOA能耗(优化后能耗)和能量优化效率.
|
|
表 1 实验1 A组的实验结果 |
|
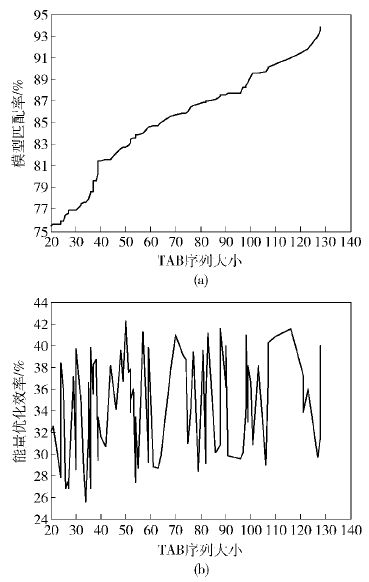
图 2 模型匹配率与能量优化效率随TAB序列值的变化趋势 |
|
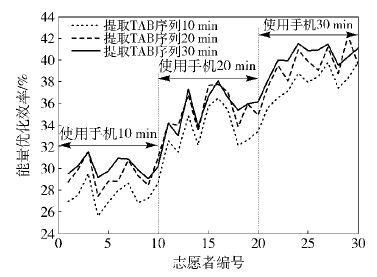
图 3 提取TAB序列10 min、20 min、30 min的能量优化效率 |
|
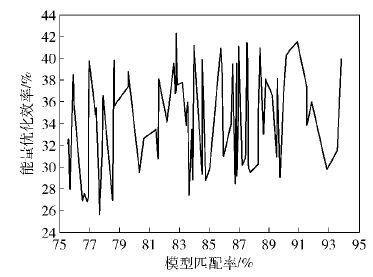
图 4 能量优化效率随模型匹配率的变化趋势 |
图 2横坐标为TAB序列值的个数,其中图 2(a)纵坐标表示模型匹配率,即使用ARMA模型预测TAB序列的准确率,图 2(b)的纵坐标表示能量优化效率,即使用BOA能达到的能量优化效果. 可以看到,模型匹配率从75.54%增长到93.86%,且基本上随TAB序列值的个数线性增长,但能量优化效率随TAB序列值个数的变化趋势不明显. 这表明TAB序列的大小对模型匹配率的影响比对能量优化效率要大得多.
图 3的横坐标为志愿者编号,纵坐标为能量优化效率. 图 3展示了使用智能手机10 min、20 min和30 min的能量优化效率. 显而易见,使用智能手机30 min的能量优化效率高于使用智能手机20 min,同样使用智能手机20 min的能量优化效率高于使用智能手机10 min,这是因为在一定范围内,使用智能手机时间越长,可优化的数据块数量越多,使得由尾巴时间引起的能量浪费就越少,能量优化率就越高. 因此,在一定范围内,使用智能手机的时间越长,BOA的能量优化效果越好. 图 4表明能量优化效率与模型匹配率之间没有直接联系,这是因为使用智能手机的时间是制约能量优化效率的一个关键性因素,使用智能手机时间的长短在很大程度上决定了设备能量优化效率的高低.
4 结束语详细分析了3G移动通信网络中尾巴时间的产生原因及其造成的能量浪费,并针对这一情况提出BOA来动态调整尾巴时间降低能耗. 在实验中,模型匹配率达到93.98%,使用BOA进行优化后的能源效率可提升42.25%. 分析结果表明,在一定范围内,提取的TAB序列个数越多,模型匹配率越高,同时使用智能手机时间越长,能量优化效果越好. 在未来的研究中,将通过完善模型定阶准则和参数估计方法来进一步提高模型的精准度;随着4G移动通信网络的不断普及,将深入探索LTE标准下的能量优化问题.
| [1] |
Park Y D, Jung K H, Suh Y J. Improving IEEE 802.11 PSM for smartphones by exploiting hidden tail-time[C]//Network of the Future (NOF), 2013 Fourth International Conference on.[S.l.]:IEEE, 2013:1-3.
( 0) 0)
|
| [2] |
Damasevicius R, Stuikys V, Toldinas J. Methods for measurement of energy consumption in mobile devices[J]. Metrology and Measurement Systems , 2013, 20 (3) :419–430.
( 0) 0)
|
| [3] |
Sheng Xiang, Tang Jian, Zhang Weiyi. Energy-efficient collaborative sensing with mobile phones[J]. Proceedings-IEEE INFOCOM , 2012, 131 (5) :1916–1924.
( 0) 0)
|
| [4] |
Schwartz C, Lehrieder F, Wamser F, et al. Smart-phone energy consumption vs 3G signaling load:the influence of application traffic patterns[C]//Digital Communications-Green ICT (TIWDC), 2013 24th Tyrrhenian International Workshop on.[S.l.]:IEEE, 2013:1-6.
( 0) 0)
|
| [5] |
Zhang Di, Zhang Yaoxue, Zhou Yuezhi, et al. Leveraging the tail time for saving energy in cellular networks[J]. IEEE Transactions on Mobile Computing , 2014, 13 (7) :1–1.
( 0) 0)
|
| [6] |
李文涛, 姜海波, 王雪琴. 自回归模型的多选择方法[J]. 统计与决策 , 2010 (18)
:28–33.
Li Wentao, Jiang Haibo, Wang Xueqin. Multiple choice method of auto regressive model[J]. Statistics and Decision Making , 2010 (18) :28–33.
( 0) 0)
|
| [7] |
付卫红, 武少豪, 张凡路, 等. 一种基于ARMA模型的欠定混合快速跳频信号参数盲估计算法[J]. 北京邮电大学学报 , 2014 (5)
:16–19.
Fu Weihong, Wu Shaohao, Zhang Fanlu, et al. A blind estimation algorithm for fast frequency hopping signals based on ARMA model[J]. Journal of Beijing University of Posts and Telecommunications , 2014 (5) :16–19.
( 0) 0)
|
| [8] |
王康, 李纪欣. Android平台休眠唤醒机制研究[J]. 计算机工程 , 2011 (S1)
:320–323.
Wang Kang, Li Jixin. Research on the mechanism of sleep wake in Android platform[J]. Computer Engineering , 2011 (S1) :320–323.
( 0) 0)
|


