针对基于二部图的概率传播(ProbS)模型以优化推荐列表的精确度为目标,而忽略了推荐多样性的问题,提出了改进的概率传播(iProbS)模型.iProbS将项目得分预测过程分解为资源的3步传播过程,每步传播包含传播概率和传播损耗.设计传播概率时,考虑的因素是用户评分;设计传播损耗时,则分别考虑了项目的度、用户熵和邻居项目.通过在2个常用数据集MovieLens和Netflix上的大量不同实验,证明了iProbS算法在推荐准确率、推荐整体多样性、推荐个体多样性以及销售平衡4个方面均比ProbS模型性能更好.最后按不同的推荐步骤分析了iProbS算法的计算复杂度.
Bipartite-graph based probabilistic spreading (ProbS) algorithms often focus on optimizing the accuracy of recommendation lists while ignoring diversity, another key property to evaluate the quality of recommendation results. In order to deal with this problem, an improved probabilistic spreading (iProbS) algorithm is proposed in the present paper. The iProbS algorithm divides the recommendation process into three steps of resource spreading, and each resource spreading step constrained by spreading probability and spreading cost simultaneously. Users' scores rating on items are applied to compute spreading probability, at the same time, the degree of items, entropy of users, and the neighbors of items are considered for computing spreading costs. Extensive experiments on two widely used data sets (from MovieLens and Netflix) show that iProbS can effectively improve recommending accuracy, aggregate diversity, individual diversity, and sales balance of recommendation lists. Finally, computational complexities of iProbS are studied from its different computing steps.
大部分的推荐算法通过预测用户对项目评分,推荐评分最高的N个项目给用户,以提升精确度,如应用最广泛的基于用户(项目)的协同过滤与矩阵分解[1-2]等. 以精确度为衡量指标的算法可能会导致两方面的问题:①流行度高的商品具有更多的历史数据,因此更容易被推荐,而那些被少部分用户购买的、目标用户可能会更喜欢的项目难以被推荐[3];②推荐的结果与用户过去的购买行为太相似,不能迎合用户的广泛喜好[4]. 提高推荐的多样性有助于解决以上问题. 许多研究者从不同方面分析了多样性[5-7]. Zhou等[7]将二部图概率传播(ProbS,probabilistic spreading)模型与一种面向多样性的热传导模型结合,以提高其推荐结果的多样性,但是会降低其精确度. 笔者同时从精确度与多样性的角度考虑对文献[7]方法的ProbS模型进行改进.
1 改进的ProbS模型在ProbS模型[7]中,如果考虑用户对项目评分的详细信息将有助于更好地计算传播概率. 同样,如果初始化中使用项目流行度来区别对待目标用户已评论过的项目,第1步传播中区分不同用户的兴趣偏好,第2步传播中考虑邻居因素计算最终项目获得的资源,将有助于进一步提高推荐的多样性与精确度性能. 基于此假设,下面给出传播过程改进的ProbS(iProbS,improved ProbS)模型.
1.1 iProbS模型概述设二部图G=(VU∪VI,E)表示用户-项目关系,其中E为边集,VU为用户集,VI为项目集. 如果u∈VU评论过项目i∈VI,则u与i之间存在一条边并且边的权重wui=wiu=rui,rui为用户u对项目i的评分.
假定目标用户u总共具有资源1,预测u对项目i的得分过程,即资源从用户u出发经过3步传播到项目i的过程. 传播过程中考虑传播概率pxy与传播损耗cxy两种情况,从节点x传播到邻居节点y的资源数为节点x具有的资源乘以传播概率再乘以传播损耗,即R(x)pxycxy,其中R(x)为x具有的资源.
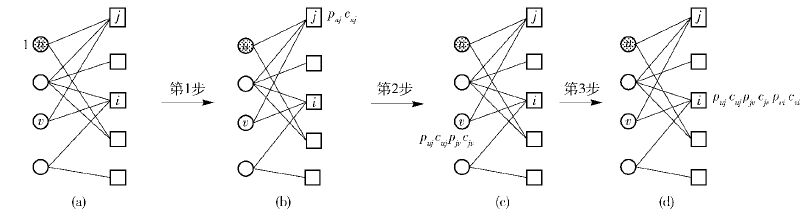
图 1描述了iProbS模型中资源通过一条路径从用户节点u传播到项目节点i的过程,项目i的最终资源为通过所有路径传播得到的资源. 预测用户u对项目i的得分即从节点u传播到节点i的资源总数:
| $\hat{r}=1\sum\limits_{j\in {{V}_{I}}}{\sum\limits_{{}}^{v\in {{V}_{U}}}{{{p}_{uj}}{{p}_{jv}}{{p}_{vi}}{{c}_{uj}}{{c}_{jv}}{{c}_{vi}}}}$ | (1) |
|
图 1 二部图中iProbS模型一条路径的传播过程 |
传播概率pxy描述了多少资源从节点x出发向节点y传播,与节点x相关,计算式如式(2)所示,且3步传播概率puj、pjv与pvi均使用式(2)计算.
| ${{p}_{xy}}=\frac{{{w}_{xy}}}{\sum\limits_{y}{{{w}_{xy}}}},{{w}_{xy}}=\left\{ \begin{matrix} {{r}_{xy}}, & x\in {{V}_{U}} \\ \text{ }{{r}_{yx}}, & x\in {{V}_{I}} \\ \end{matrix} \right.$ | (2) |
传播损耗cxy描述了资源在传播过程中的损耗情况,与节点y相关. 下面区分3步传播中的不同节点y,考虑3种因素计算传播损耗.
第1步传播中,如不考虑传播损耗的情况,则用户u的邻居项目j收到的资源与其度成正比,即评论过项目j的用户越多,项目j收到的资源就越多. 因此,流行度高的项目的推荐能力得到了加强而流行度低的项目的推荐能力得到了减弱. 因此考虑到项目的度,将第1步传播中的损耗定义为
第2步传播中,假设两用户u1和u2中u1具有少量的评分数据并且兴趣专一,u2具有大量的评分数据,并且兴趣广泛,如果两个项目同时被一个用户评论,那么同时被用户u1评论应该比同时被u2评论更相似. 因此,增加兴趣特殊的用户推荐能力,降低兴趣广泛的用户推荐能力有助于发现更准确的项目和更个性化的项目. 因此使用用户熵来计算第2步传播中的损耗,即
第3步传播中,如不考虑传播损耗的情况,节点v会将资源传播到其所有邻居节点. 考虑一种极端情况:用户u评论过100部电影,每部电影又被100个用户评论过,并且这些用户又评论过100部电影,所有用户与电影均不重复,则按照传播过程描述能被传播到资源的项目有近100万部,这样将发现大量不相关的电影,然而推荐列表的长度往往非常短(如10). 虽然这种情况几乎不可能发生,但是传播得到的项目个数也非常多,许多与目标用户兴趣并不相关的项目也得到了资源,并且最终流行度高的项目倾向于获得更多的资源,导致为许多用户推荐相同的高流行度的项目. 因此,引入邻居概念,当项目i不属于目标用户u评论过的项目j的最近邻居项目时,则不进行传播,传播损耗计算式为cvi=|KNN(j)∩{i}|,其中KNN(j)表示j的K个最近邻居项目集. 最近邻居选取与项目j相似度最高的项目,相似度sij使用cosin相似度并基于用户对项目的评分信息来计算,即
| ${{s}_{ij}}=\frac{\sum\limits_{v\in {{V}_{U}}}{{{r}_{vi}}{{r}_{vj}}}}{\sqrt{\sum\limits_{v\in {{V}_{U}}}{{{r}_{vi}}^{2}\sqrt{\sum\limits_{v\in {{V}_{U}}}{{{r}_{vj}}^{2}}}}}}$ |
在为单个用户推荐项目的时候,使用式(1)可以快速方便地得到推荐结果. 考虑到在为所有用户推荐时,不同用户的资源会经过二部图中同一条边多次. 为避免大量重复计算,在改进的模型具体实现时先计算项目-项目传播矩阵T:
| ${{t}_{ij}}=\sum\limits_{{}}{{{p}_{jv}}{{p}_{vi}}{{c}_{jv}}{{c}_{vi}}}$ |
然后为每个目标用户评论过的项目分配资源fuj=pujcuj,最终传播结果项目得分为
算法1 iProbS.
输入: A; 输出: L.
1) 根据评分矩阵A构建用户-项目二部图G;
2) 根据评分矩阵A计算项目-项目相似度矩阵S;
3) 根据G和S计算项目-项目传播矩阵T;
4) 为每个用户预测项目的得分,具体如下:
① FOR each u in U:
② FOR each i in I:
③FOR each j in I(u):
④
5) 为每个用户u从R(u)中选择得分最大的N个未看过的项目添加到L(u).
2 实验表 1描述了两个数据集的详细信息. 每个数据集都包含了用户对电影的评分信息,分数为1~5分. 随机选取数据集中20%作为测试集,剩余的作为训练集. 5种对比算法分别为基于用户的协同过滤(UB,user based)、基于用户的最近邻协同过滤(UBKNN,user based K-nearest neighbors)[8]、矩阵奇异值分解(SVD++,singular value decomposition)[3]、ProbS模型[7]、iProbS模型. 其中,对于UBKNN,设邻居个数为50;对于SVD++,使用印桂生等[3]提出的SVD++,并设置因子个数为50;对于iProbS模型,在MovieLens上设置邻居个数K为50,而在Netflix上设置邻居个数K为5. 根据预测得分,依次按照不同的推荐列表长度(1~50)为用户推荐电影.
|
|
表 1 数据集详细信息 |
1) 准确率. 计算公式为
| $P=\sum\limits_{u\in {{U}_{T}}}{\frac{\sum\limits_{i\in {{L}_{u}}}{{{1}_{{{r}_{ui}}\ne 0}}}}{N|{{U}_{T}}|}}$ |
其中:UT为测试集中用户的集合,Lu为用户u推荐的项目集合,rui为测试集中用户u对项目i的评分,N为推荐列表的长度.
2) 整体多样性. 计算公式为
3) 销售平衡. 使用基尼系数可以衡量整体多样性中商品的销售平衡,计算公式为
| $G=\frac{2}{n-1}\sum\limits_{i=1}^{n}{\left( n+1-i \right)\frac{n\left( i \right)}{N|{{U}_{T}}|}}.$ |
其中:n为项目总数,n(i)为项目i被推荐给不同用户的次数.
4) 个体多样性. 个体多样性用所有项目对之间相似度之和平均值的方法来衡量,表示为
| $\beta =\frac{1}{|{{U}_{T}}|}\sum\limits_{u\in {{U}_{T}}}{\frac{1}{N\left( N-1 \right)}}\sum\limits_{i,j\in {{L}_{u}};i\ne j}{{{s}_{ij}}}$ |
其中sij为训练集中项目i与项目j的相似度.
2.2 实验结果表 2为不同数据集、不同推荐列表长度下,各对比算法在整体多样性α (表中的数字内容即整体多样性α值)方面的表现. 如表 2所示,iProbS明显优于ProbS,并且同时明显优于其他3种协同过滤算法. 例如,在MovieLens中推荐列表长度N=10时,iProbS的整体多样性为2 373,而ProbS仅仅只有109,其他算法中表现最好的UBKNN也仅有587.
|
|
表 2 不同算法在整体多样性方面的表现 |
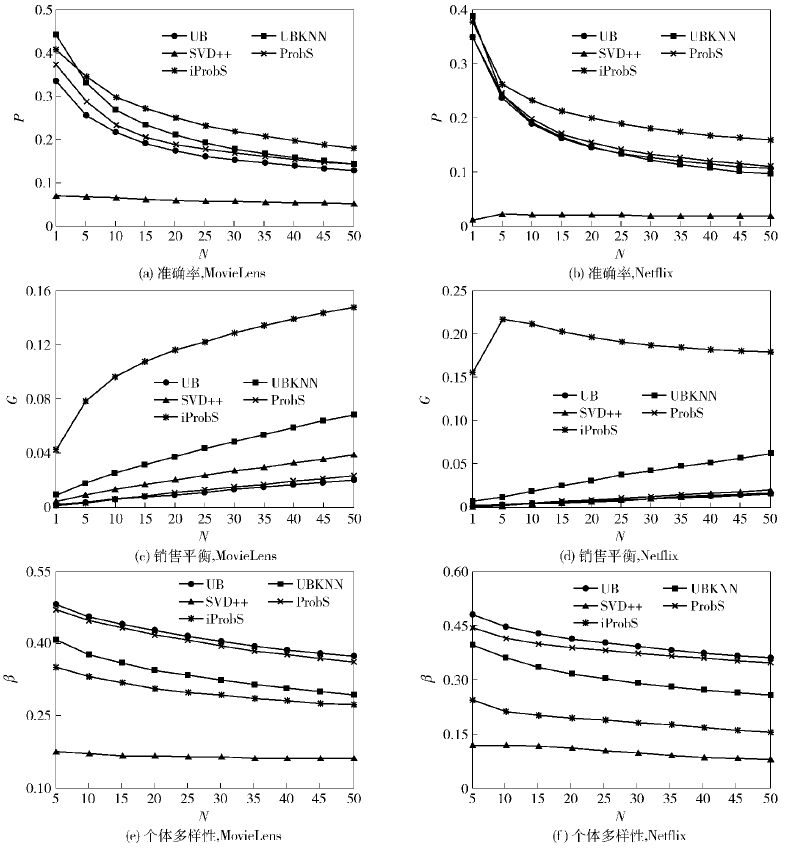
图 2(a)、(b)描述了各算法在准确率P方面的表现;图 2(c)、(d)描述了各个算法在销售平衡基尼系数G方面的表现;图 2(e)、(f)描述了各个算法在个体多样性β方面的表现.
|
图 2 不同算法在准确率、销售平衡、个体多样性方面的表现 |
综合所有实验结果的4种评价指标来看,由于iProbS算法考虑了项目评分的详细信息,抑制了高流行度项目的推荐能力,提高了兴趣专一用户的推荐能力,并且只为目标用户已评论过项目的最近邻居项目传播资源,排除了不相关项目的干扰,所以不仅能获得更好的精确度,还能获得更好的整体多样性、销售平衡与个体多样性. 虽然SVD++在个体多样性上优于iProbS,但是其代价是非常低的精确度.
2.3 复杂度分析iProbS比ProbS在传播过程中多考虑了一些因素,一定程度上对ProbS的时间复杂度低这一优点产生了影响. 假定测试集中用户与项目的度平均值分别为ku与ko,邻居个数为K,预测结果中用户的非零得分项目的平均个数为nR,则ProbS的时间复杂度为O(nkoku+mnku+mnRlg nR). 由于mku=nko,替换得到时间复杂度为O(mku2+mnku+mnR×lg nR),并且一般情况下ku2<<nku,因此ProbS最终的时间复杂度为O(mnku+mnRlg nR). iProbS的时间复杂度为O(nkoku+mku2K+mnku+mnRlg nR),同样地,替换nko=mku得到iProbS最终的时间复杂度为O(mku2K+mnku+mnRlg nR). 可以看出,iProbS在计算传播矩阵时复杂度为mku2N,高于ProbS;同样地,iProbS使用了邻居思想导致nR的值远远小于ProbS中nR的值,因此选择N个进行推荐时运行时间会比ProbS低. 表 3描述了不同算法在MovieLens数据上为所有用户推荐N=10个项目时的运行时间,其中值为0表示该算法不需要相应步骤.
|
|
表 3 不同算法在MovieLens中的运行时间 |
精确度与多样性均是衡量推荐结果好坏的重要指标. 笔者同时从精确度与多样性角度考虑,对文献[7]中所述的ProbS模型进行了改进,将资源的传播过程进一步分析为由传播概率与传播损耗两部分决定,并且分别考虑不同的因素为3步传播计算不同的传播损耗. 两种常用数据集上的实验从准确率、整体多样性、个体多样性与销售平衡4个方面证明了改进模型在精确度和多样性方面的有效性,并且与应用广泛的协同过滤算法进行了对比,最后通过对时间复杂度的分析以及实验验证了改进模型保留了基本ProbS模型复杂度低的优点. 如何考虑多种因素计算传播损耗以更好地调节精确度与多样性之间的折中是需要进一步研究的方面.
| [1] |
Adomavicius G, Tuzhilin A. Toward the next generation of recommender systems:a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge and Data Engineering , 2005, 17 (6) :734–749.
doi:10.1109/TKDE.2005.99 ( 0) 0)
|
| [2] |
蔡国永, 吕瑞, 樊永显. 基于标签和因子分析的协同推荐方法[J]. 北京邮电大学学报 , 2015, 38 (3)
:34–38.
Cai Guoyong, Lü Rui, Fan Yongxian. Collaborative recommendation method based on tags and factor analysis[J]. Journal of Beijing University of Posts and Telecommunications , 2015, 38 (3) :34–38.
( 0) 0)
|
| [3] |
印桂生, 张亚楠, 董红斌, 等. 一种由长尾分布约束的推荐方法[J]. 计算机研究与发展 , 2013, 50 (9)
:1814–1824.
Yin Guisheng, Zhang Yanan, Dong Hongbin, et al. A long tail distribution constrained recommendation method[J]. Journal of Computer Research and Development , 2013, 50 (9) :1814–1824.
( 0) 0)
|
| [4] |
Adamopoulos P, Tuzhilin A. On over-specialization and concentration bias of recommendations:probabilistic neighborhood selection in collaborative filtering systems[C]//Proceedings of the 8th ACM Conference on Recommender systems. New York:ACM, 2014:153-160.
( 0) 0)
|
| [5] |
Adomavicius G, Kwon Y O. Improving aggregate recommendation diversity using ranking-based techniques[J]. IEEE Transactions on Knowledge and Data Engineering , 2012, 24 (5) :896–911.
doi:10.1109/TKDE.2011.15 ( 0) 0)
|
| [6] |
Vargas S, Castells P. Improving sales diversity by recommending users to items[C]//Proceedings of the 8th ACM Conference on Recommender Systems. New York:ACM, 2014:145-152.
http://cn.bing.com/academic/profile?id=2086456706&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| [7] |
Zhou Tao, Kuscsik Z, Liu Jianguo, et al. Solving the apparent diversity-accuracy dilemma of recommender systems[J]. Proceedings of the National Academy of Sciences , 2010, 107 (10) :4511–4515.
doi:10.1073/pnas.1000488107 ( 0) 0)
|
| [8] |
Lü Linyuan, Medo M, Yeung C H, et al. Recommender systems[J]. Physics Reports , 2012, 519 (1) :1–49.
( 0) 0)
|


