干扰对齐是一种新兴的干扰管理机制，相对传统的频分复用技术，采用干扰对齐技术可以大大增加系统的信道容量^[1-4]. 对于一个频域多信道无线网络，若独立衰落的信道数为M，并且网络内每个用户仅需传输一路数据流，则该网络最多可容纳2M-2个用户同时进行通信，且系统可表示为(M×M, 1)^2M-2[4]. 笔者以系统网络和速率为优化目标函数，提出了一种利用梯度改进粒子群的优化算法(Grad-PSO,gradient-exploited particle swarm optimization algorithm)，以解决频域干扰对齐全局最优解搜索问题. 该算法继承了粒子群算法实现简单、对多峰值问题的较强全局搜索能力等特性，并在此基础上利用目标函数梯度对其做出改进，加强了算法全局搜索能力和收敛速度，从而可以以更高的概率获得网络和速率性能更好的干扰对齐解.

1 系统模型

考虑K用户频域多信道单输入单输出系统，假设发射信号编码于M个相互正交的独立衰落频域信道之间，则系统可容纳K=2M-2个用户进行通信，系统的输入输出关系可表述为矩阵形式^[4]：

${{Y}^{k}}=\sum\limits_{l=1}^{K}{{{H}^{kl}}{{X}^{l}}+{{Z}^{k}}={{H}^{kk}}{{X}^{k}}+}\sum\limits_{l\ne k}^{K}{{{H}^{kl}}{{X}^{l}}+{{Z}^{k}}}$

(1)

其中：H^kl=diag{h^kl[f₁],h^kl[f₂],…,h^kl[f_M]}为对角信道矩阵，h^kl[f_j]表示第l个发射机和第k个接收机之间第j个独立衰落信道的衰落系数；Z^k为均值为0、方差为1的加性高斯白噪声，即$E[{{Z}^{k}}{{({{Z}^{k}})}^{H}}]=I;{{X}^{l}}=\sqrt{{{P}^{l}}}{{V}^{l}}{{x}^{l}}$为第l个发射机的发射信号，E[‖X^l‖²]=P^l，其中V^l为第l个发射机的预编码向量(为单位向量)，标量x^l表示第l个发射机的数据流. 干扰对齐的目标是设计每个发射机预编码向量V^l(l∈{1,2,…,K})，以使得在每个接收机所接收到的干扰信号全部约束至一个超平面内，该超平面即干扰子空间，而期望信号独立于干扰子空间. 这样第k个接收机可使用相应的干扰抑制矩阵U^k(k∈{1,2,…,K})迫零滤除所有的干扰信号，提取出期望信号. 即干扰对齐解应满足

$\left. \begin{matrix} {{({{U}^{k}})}^{H}}{{H}^{kl}}{{V}^{l}}=0, & \forall k\ne l \\ {{({{U}^{k}})}^{H}}{{H}^{kk}}{{V}^{k}}\ne 0 & k\in \left\{ 1,2,\ldots ,K \right\} \\ \end{matrix} \right\}\text{ }$

(2)

2 网络和速率及其梯度

类似于多输入多输出干扰对齐系统^[5]，频域干扰对齐系统的网络和速率为系统的信道容量总和：

$R=\sum\limits_{k=1}^{K}{lb|I+{{({{B}^{k}}+{{I}_{N}})}^{-1}}{{A}^{k}}|~}$

(3)

其中：A^k=H^kkV^k(V^k)^H(H^kk)^HP^k为用户k的期望信号自相关矩阵，${{B}^{k}}=\sum\limits_{l\ne k}{{{H}^{kl}}{{V}^{l}}{{({{V}^{l}})}^{H}}{{({{H}^{kl}})}^{H}}{{P}^{l}}}$为用户k干扰信号自相关矩阵，I_N为高斯白噪声的自相关矩阵，P^k为用户k的发射功率.

因此，所需要解决的问题就是，利用粒子群算法，求解如式(4)所示的优化问题：

$\begin{align} & max~R({{V}^{1}},{{V}^{2}},\ldots ,{{V}^{K}}) \\ & s.t.~{{({{V}^{k}})}^{H}}{{V}^{k}}=1 \\ \end{align}$

(4)

文献^[5-6]给出了网络和速率的导数的推导过程，首先经数学推导，网络和速率可以表示为

$\begin{align} & R=\sum\limits_{k=1}^{K}{(lb|{{A}^{k}}+{{B}^{k}}+{{I}_{N}}|+lb|{{B}^{k}}+{{I}_{N}}|)=} \\ & \sum\limits_{k=1}^{K}{({{\Phi }_{k}}+{{\Psi }_{k}})} \\ \end{align}$

(5)

其中Φ_k、Ψ_k分别为网络和速率的第1部分和第2部分. 基于式(5)网络和速率关于发射预编码V^k的梯度可以很容易推导出来.

根据微分公式d(ln |Q|)=tr{Q^-1dQ}，Φ_k、Ψ_k关于第k个用户的发射预编码V^k的梯度分别为

$\frac{\partial {{\Phi }_{l}}}{\partial {{V}^{(k)}}}=\frac{2{{P}^{k}}}{ln~2}{{({{H}^{lk}})}^{H}}{{({{A}^{k}}+{{B}^{k}}+{{I}_{N}})}^{-1}}{{H}^{lk}}{{V}^{k}}$

(6)

$\frac{\partial {{\Psi }_{l}}}{\partial {{V}^{(k)}}}=\frac{2{{P}^{k}}}{ln~2}{{({{H}^{lk}})}^{H}}{{({{B}^{k}}+{{I}_{N}})}^{1}}{{H}^{lk}}{{V}^{k}}$

(7)

因此，由式(5)可得网络和速率关于第k个用户的发射预编码V^k的梯度函数为

${{\Delta }_{k}}R=\sum\limits_{l=1}^{K}{\frac{\partial {{\Phi }_{l}}}{\partial {{V}^{k}}}}~-\sum\limits_{l\ne k}{\frac{\partial {{\Psi }_{l}}}{\partial {{V}^{k}}}}$

(8)

3 基于粒子群优化的干扰对齐最优解搜索算法 3.1 粒子群算法

粒子群算法是Eberhart和Kennedy受鸟群运动模型的启发，提出的一种智能全局搜索算法^[7]. 粒子群算法将鸟群运动模型中的栖息地类比为实际问题的搜索空间，将鸟群中的个体抽象为K维搜索空间中没有质量和体积的粒子，每个粒子以一定的速度在搜索空间中运动，通过相互协作、信息共享，向自身历史最佳和全局最佳位置聚集，从而实现对全局最优解的搜索. 假设群体中有N个粒子，则粒子i的第k维的速度和位置按式(9)进行更新.

$\left. \begin{matrix} {{W}_{i}}^{k}={{W}_{i}}^{k}+{{c}_{1}}{{r}_{1}}({{b}_{i}}^{k}-{{V}_{i}}^{k})+{{c}_{2}}{{r}_{2}}({{g}^{k}}-{{V}_{i}}^{k}) \\ {{V}_{i}}^{k}={{V}_{i}}^{k}+{{W}_{i}}^{k} \\ \end{matrix} \right\}$

(9)

其中：V_i=(V_i¹,V_i²,…,V^K_i)、W_i=(W_i¹,W_i²,…,W^K_i)分别为粒子i的位置和搜索移动速度；b_i=(b_i¹,b_i²,…,b^K_i)为粒子i的自身历史最佳位置，即粒子i在搜索过程中经历过的最优目标函数值对应的粒子位置；g=(g¹,g²,…,g^K)为整个种群的历史最佳位置，即整个种群在搜索过程中经历过的目标函数值最优的位置；c₁和c₂分别为反映粒子向自身最佳位置和种群历史最佳位置运动的加速因子；r₁和r₂分别为[0,1]范围内的随机数.

3.2 算法改进

粒子群算法是一种典型的解决复杂多峰值问题的数值搜索算法，但是频域干扰对齐系统的解空间非常复杂，具有丰富的局部最优值，并且随着通信系统中用户数的增加，信噪比的升高，干扰对齐解空间的复杂性会越来越高，局部最优值越来越多，导致粒子群算法的全局搜索能力会变得不足，甚至无法求解. 因此针对干扰对齐解空间的特点对粒子群算法做两个方面的改进.

1) 由于通信系统中各个用户的发射预编码向量均为单位向量，而粒子i的第k维在位置V_i^k经速度W_i^k更新后，其新位置V_i^k+W_i^k可能已经不是单位向量了，不满足编码向量条件，因此需要将V_i^k+W_i^k在单位向量球面上进行投影来归一化，即在干扰对齐最优解搜索问题中，粒子群的位置变化相当于将更新前的单位预编码向量保持模不变、方向偏移一个特殊角度(该角度由速度向量W_i^k决定)后获得的单位向量作为新的粒子群位置. 而速度向量W_i^k在预编码向量V_i^k方向上的分量对于位置向量的方向变化是无用的. 故改进算法取速度向量W_i^k在编码向量V_i^k的法平面上的投影向量作为最终的速度向量以扩大算法的搜索范围，即将式(9)进行优化，具体操作如式(10)所示.

$\left. \begin{matrix} {{W}_{i}}^{k}={{W}_{i}}^{k}+{{c}_{1}}{{r}_{1}}({{b}_{i}}^{k}-{{V}_{i}}^{k})+{{c}_{2}}{{r}_{2}}({{g}^{k}}-{{V}_{i}}^{k}) \\ {{W}_{i}}^{k}={{W}_{i}}^{k}-{{V}_{i}}^{k}{{({{({{V}_{i}}^{k})}^{H}}{{V}_{i}}^{k})}^{-1}}{{({{V}_{i}}^{k})}^{H}}{{W}_{i}}^{k} \\ {{V}_{i}}^{k}=\frac{{{V}_{i}}^{k}+{{W}_{i}}^{k}}{\|{{V}^{k}}_{i}+{{W}^{k}}_{i}\|} \\ \end{matrix} \right\}$

(10)

2) 粒子群算法每次位置更新后的搜索结果并不能保证优于前一次，因此它趋向于全局最优的能力不足，收敛速度不够快. 改进算法利用第2节根据文献^[5-6]得出的网络和速率R(V_i)相对于每个用户编码向量V_i^k的梯度Δ_kR，在位置更新之后增加一次沿网络和速率函数梯度方向的学习搜索，以提升算法趋于全局最优的能力，加快算法的收敛速度，如式(11)所示.

${{V}_{i}}^{k}=\frac{{{V}_{i}}^{k}+\lambda {{\Delta }_{k}}R}{\|{{V}_{i}}^{k}+\lambda {{\Delta }_{k}}R\|}~$

(11)

其中λ为搜索步长.

3.3 基于Grad-PSO的干扰对齐解搜索算法

根据前述内容，基于Grad-PSO的干扰对齐解搜索算法实现步骤如下.

1) 粒子初始化. 初始化粒子的初始位置，即编码向量V_i，初始化粒子运动速度W_i，并计算相应的网络和速率R(V_i)、个体的历史最优位置b_i和种群历史最优位置g，初始化惯性权重ω=0.728 9，加速因子c₁=2.05、c₂=2.05，种群中粒子个数为N，最大迭代次数为T.

2) 初始化粒子序列号i=1.

3) 按式(10)更新粒子运动速度W_i^k和粒子位置V_i^k，1≤k≤K.

4) 按式(8)计算梯度Δ_kR，并沿Δ_kR的方向进行搜索，即求解方程$\underset{\lambda }{\mathop{\max imizexR}}\,$(V_i^k+λΔ_kR).

5) 按式(11)更新编码向量V_i^k，1≤k≤K.

6) 若R(V_i)>R(b_i)转到7)，否则转到8).

7) 更新b_i和g，具体如式(12)所示.

$\left. \begin{matrix} {{b}_{i}}={{V}_{i}} \\ g=\left\{ \begin{matrix} {{V}_{i}},\text{ }R({{V}_{i}})>R\left( g \right) \\ g,\text{ }R({{V}_{i}})~<R\left( g \right) \\ \end{matrix} \right. \\ \end{matrix} \right\}$

(12)

8)若i<N，则i=i+1，并转到3).

9)若t<T，则t=t+1，并转到2)，否则结束.

4 性能分析 4.1 仿真分析

为验证基于Grad-PSO的频域干扰对齐算法对频域干扰对齐系统全局最优解搜索的有效性，将Grad-PSO算法与功率渐变下的梯度上升算法(GAPI,gradient ascend algorithm with power increase)^[6]以及最大化信干噪比算法(Max-SINR,maximize signal to interference plus noise ratio)和最小化干扰泄露算法(Min-IL,minimum interference leakage)两个经典的迭代干扰对齐算法^[8]的总信道容量进行仿真对比. 本节给出4种算法在频域多信道干扰对齐系统下进行若干次独立实验后取统计平均的数值仿真结果. 为公平起见，仿真按以下规则进行：①对于两种经典算法和GAPI算法，每一次独立实验均以相同的任意随机单位预编码向量组V^k(1≤k≤K)开始搜索，初始化GAPI的参数：初始信噪比γ₀=-10 dB，功率迭代倍率ρ=1.1，并迭代足够多的次数以使得算法收敛；②对于Grad-PSO算法，粒子群个体数N为30，即有30个预编码向量组V_i^k(1≤k≤K)，初始化每个个体使其均为任意随机单位向量组，其中随机选取一个个体，将其初始化为与另外3种算法相同的预编码向量V^k,1≤k≤K，初始化每个个体的移动速度向量W_i^k(1≤k≤K)使其均为任意随机单位向量，同样迭代足够多的次数以使得算法收敛.

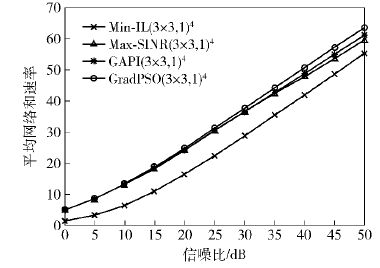
根据文献^[4]的结论，对于频域多信道单输入单输出系统，M个独立衰落信道可容纳2M-2个用户通信. 图 1、图 2分别给出了(3×3，1)⁴和(4×4，1)⁶两种情况下的系统网络和速率仿真结果.

对比图 1、图 2可以得出以下结论：

1) 迭代Min-IL算法的性能明显差于其他3种算法. 这是因为频域多信道干扰对齐系统是一个欠定系统，它具有无数个可行解和丰富的局部最优解. 迭代Min-IL算法的优化目标为最小化干扰信号的泄露能量，不考虑最大网络和速率，因此一旦足够逼近任意一个干扰对齐解时，该算法将收敛并停止迭代，因此其性能明显差于其他3种算法.

2) 在低信噪比区域Grad-PSO算法和GAPI算法的性能几乎和迭代Max-SINR算法一样，而在中高信噪比区域明显高于迭代Max-SINR算法.

由于频域多信道干扰系统的干扰对齐解空间复杂性是随发射信号功率变化的，发射功率水平较低(低信噪比区域)时，解空间复杂度相对较低，且当发射功率趋于0时，网络和速率函数将只有单一的全局最优值^[6]，所以在低信噪比区域，Max-SINR算法可以与Grad-PSO算法和GAPI算法获得相近的网络和速率. 随着信噪比的增大，干扰信号能量也随之增大，从而干扰对齐解空间上会凸显出越来越多的局部最优解，导致迭代Max-SINR 算法收敛于局部最优解的概率越来越大. 因此在中高信噪比区域，Grad-PSO算法和GPIA算法获得的(平均)网络和速率性能优于迭代Max-SINR 算法.

3) 由于随着信道和用户数的增加，发射预编码的维度会越来越高，干扰对齐解空间会越来越复杂，导致迭代Max-SINR 算法收敛于局部最优解的概率越来越大. 因此对比图 1和图 2，随着信道和用户数的增加，Grad-PSO与GAPI算法相对于Max-SINR 算法性能提升更加明显.

4) 随着信噪比的升高以及信道和用户数的增加，干扰对齐解空间会越来越复杂. Grad-PSO算法相对于GAPI算法有更广的搜索范围，更强的全局搜索性能，在多次独立实验中可以以更高的概率获得最优干扰对齐解. 所以Grad-PSO算法可以获得比GAPI算法更好的(平均)网络和速率性能.

4.2 复杂度分析

GAPI算法和Grad-PSO算法都是集中式的干扰对齐解全局搜索算法，因此将Grad-PSO算法计算复杂度与GAPI算法进行对比.

GAPI算法本质上是一个网络和速率梯度上升搜索算法，在此基础上增加功率渐变机制，即在特定的信噪比下，使算法从一个足够小的信号功率值开始迭代搜索并收敛后，更新信号功率值再次搜索，以保证迭代解能够跟踪和速率函数的渐变过程，满足收敛解能够一直位于网络和速率函数的极值点处^[6]. GAPI算法的具体实现步骤如下.

1) 初始化所有预编码向量V^k(k∈{1,2,…,K})，使原始功率$P={{10}^{\frac{\gamma 0}{10}}}$，设置功率迭代倍率ρ(1<ρ<1.2)以及迭代步长λ，最大迭代次数为T；

2) 由ρP→P设置信道的迭代功率；

3) 由式(8)计算和速率函数梯度Δ_kR ；

4) 由$\mathop {maximizeR}\limits_\lambda ({V_i}^k + \lambda {\Delta _k}R)$进行一维搜索，获得步长参数λ；

5) 由式(11)更新向量V^k(k∈{1,2,…,K})；

6) 若t<T，则t=t+1，返回3)；

7) 返回2)，直至功率迭代完成.

Grad-PSO算法和 GAPI 算法的计算量都主要集中在每一次预编码向量迭代更新的搜索过程中，该过程中Grad-PSO算法主要包括法平面投影计算、梯度上升算法计算，GAPI算法主要包括梯度上升算法计算. 由于梯度上升算法的计算量要远远高于投影计算，即Grad-PSO 算法和 GAPI 算法一次预编码向量更新搜索的时间计算量相当. 所以两种算法的时间复杂度差异主要体现在其在特定信噪比下的预编码向量更新搜索的迭代次数上. 在给定信噪比下，Grad-PSO 算法的搜索次数为粒子数N乘以迭代次数T，即复杂度为O(NT) ；假设GAPI算法的功率渐变迭代次数为L，其搜索次数为功率渐变迭代次数L乘以迭代次数T，即复杂度为O(LT) . 而$\left\lceil {\frac{{lgP - lg{P_0}}}{{lg\rho }}} \right\rceil = \left\lceil {\frac{{\gamma - {\gamma _0}}}{{10lg\rho }}} \right\rceil $，随着信噪比的增大而增大，所以GAPI算法的复杂度也随信噪比的增大而增高. 例如，当ρ取1.2和1.1，γ₀ 取-10 dB时，功率渐变迭代次数L随信噪比的变化规律如表 1所示.

由表 1可知，当γ>15 dB时， L>N=30 ，由于1<ρ<1.2，所以至少在γ>15 dB的高信噪比区域GAPI算法的复杂度要高于Grad-PSO 算法. 而由4.1节的分析可知，干扰对齐的性能优势主要体现高信噪比区域，因此在实际应用中Grad-PSO 算法的时间复杂度要低于GAPI算法.

5 结束语

为了能获得频域多信道干扰对齐系统的最优网络和速率，以系统网络和速率为优化目标，对粒子群优化算法进行两点改进，使之适合用于单数据流频域多信道干扰对齐系统最优解的搜索问题. 仿真结果表明，所提出的Grad-PSO算法可以获得比Min-IL算法、Max-SINR算法和GAPI算法更好的网络和速率，有效实现了干扰对齐技术的性能优势.