现有集中式多跳网络研究对其性能的建模分析较少考虑协议参数的影响,使实际场景中的协议设计缺乏理论依据.针对这一问题,充分考虑网络参数、业务参数、协议参数的影响,建立了集中式多跳网络调度时延模型和有效吞吐量模型.该模型和数值仿真结果揭示了网络节点个数、网络总带宽、业务流数目、平均跳数、控制时隙比例、最大可预约时隙个数等参数对系统性能的影响.最后给出了特定网络场景和业务需求条件下的控制时隙比例和最大可预约时隙个数等协议参数的优化策略.
In the existing literature of performance modeling and analysis of centralized multi-hop networks, the models almost did not deal with the impacts of protocol parameters, resulting in lack of theoretical support for the protocol design in practical scenarios. Regarding this problem, the schedule delay and effective throughput models which fully consider the network parameters, service parameters as well as protocol parameters were proposed. The models and numerical simulation show the impacts of parameters such as the number of nodes, network bandwidth, the number and average hop-count of service flows, proportion of control slots and bit number within one slot. The optimization strategy of proportion of control slots and bit number within one slot under various network scenarios and service requirements were further obtained.
集中式多跳网络可有效突破蜂窝网络一跳和两跳的局限,并能有效解决竞争机制存在的性能问题. 集中式多跳网络具有控制稳定、冲突较小、资源利用率较高等特点[1],因此在未来5G网络、物联网、机器对机器(M2M,machine to machine)网络中具有广泛的应用前景.
集中式组网技术研究由来已久,其中针对一跳网络的研究[2, 3]相对成熟. 长期演进的演进(LTE-A,long term evolution-advanced)中引入中继Relay和多点协作(CoMP,coordinated multiple points)传输技术实现两跳通信,但其研究成果[4, 5]很难拓展至多跳网络. IEEE 802.16定义了无线网格网络Mesh模式[6]以支持多跳,其预约机制可有效保障系统性能,但现有协议只定义了基本框架,具体机制的设计尚有空白. 诸多研究[7]针对Mesh模式扩充并完善了关键机制和算法,但各文献在分析系统性能指标时,既没有考虑协议参数的影响,也没有考虑网络场景和业务需求多样化带来的问题,其研究成果很难指导工程实用化中的协议设计和优化,导致实际场景中的协议设计缺乏理论依据.
针对上述问题,笔者充分考虑网络参数、业务参数和协议参数的影响,以集中式调度协议框架为基础,建立了集中式多跳网络调度时延模型和有效吞吐量模型,通过模型和数值仿真分析了网络节点个数、网络总带宽、业务流数目、平均跳数、控制时隙比例、最大可预约时隙个数等参数对系统性能的影响,最终给出了特定网络场景和业务需求条件下的协议参数优化策略.
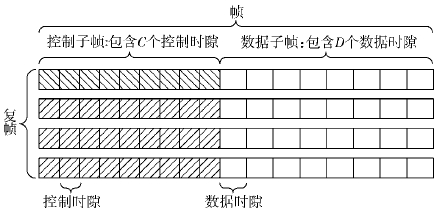
1 集中式调度协议框架集中式多跳网络由基站和用户站节点组成,构成以基站为根节点的调度树状结构. 集中式调度协议框架下的帧结构如图 1所示. 控制信道和数据信道在时间上分离,最小单位分别为控制时隙和数据时隙. C个控制时隙构成控制子帧,D个数据时隙构成数据子帧,控制子帧和数据子帧组成1帧. 连续若干个帧构成1个复帧.
控制时隙用于传输控制消息. 控制消息包括网络配置消息(NCFG,network configuration)、集中式调度配置消息(CSCF,centralized schedule configuration)、集中式调度申请消息(CSCR,centralized schedule request)和集中式调度授权消息(CSCG,centralized schedule grant). 数据时隙则用于传输用户数据.
在集中式多跳网络中,全网完成1次周期性功能的时间称为调度周期. 在调度周期内,各节点间通过资源预约以实现数据传递. 这一过程称为数据调度过程,可由“配置—申请—授权”过程来描述. 具体包括:首先基站发送CSCF消息,其他节点按层次遍历的顺序逐节点转发携带调度树信息的CSCF直至全网接收;其次末子站发送CSCR消息,其他节点按层次遍历顺序的反序逐节点发送携带各节点申请信息的CSCR直至基站接收;最后基站发送CSCG消息,其他节点按层次遍历的顺序逐节点转发携带资源分配结果的CSCG直至全网接收.
2 性能建模 2.1 调度时延模型时延主要包括排队时延、处理时延、调度时延等. 从协议角度分析,调度时延最为主要,排队时延、处理时延等与之相比可忽略. 笔者主要建立调度时延模型.
假设在集中式多跳网络中有N个节点,按照层次遍历的顺序编号为1,2,…,N. 节点i(i=1,2,…,N)的调度时延TD(i)定义为业务流到达时刻至基站(BS,base station)所有授权生效时刻所需的时间. 因此,调度时延TD(i)包括3个部分:等待时间Tw(i)、请求时间Tr(i)和授权时间Tg(i). 关系为
| ${T_{\text{D}}}\left( i \right) = {T_{\text{w}}}\left( i \right) + {T_{\text{r}}}\left( i \right) + {T_{\text{g}}}\left( i \right)$ | (1) |
其中:Tw(i)为等待时间,指业务流到达至节点发送申请消息所需的时间;Tr(i)为请求时间,指节点发送申请消息至基站收到所有申请消息的时间;Tg(i)为授权时间,指基站开始发送授权消息至所有节点成功接收授权消息的时间.
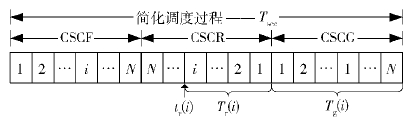
假设用于数据调度的时隙是连续的,则数据调度过程可简化为图 2,数字1,2,…,N表示在该时隙发送消息的节点编号.
假设业务流服从泊松过程,则在1个调度周期中业务到达时刻ta为均匀分布. 对于节点i,CSCR发送时刻为tr(i),则等待时间为
| ${T_{\text{w}}}\left( i \right) = \left\{ \begin{gathered} {t_{\text{r}}}\left( i \right) - {t_{\text{a}}},\;\;{t_{\text{r}}}\left( i \right) > {t_{\text{a}}} \hfill \\ {T_{\sec }} + {t_{\text{r}}}\left( i \right) - {t_{\text{a}}},\;\;{t_{\text{r}}}\left( i \right) \leqslant {t_{\text{a}}} \hfill \\ \end{gathered} \right.$ | (2) |
其中Tscc为调度周期内用于调度的控制时隙总数. 由图 2易知,Tscc=3N,Tr(i)=i,Tg(i)=N,因此TD(i)的期望值为
| $E\left( {{T_{\text{D}}}\left( i \right)} \right) = \frac{5}{2}N + i + \frac{1}{2}$ | (3) |
调度周期的时长一般设为复帧周期的整数倍,若以s为单位,调度周期的期望值可表示为
| $E\left( {{T_{\text{D}}}\left( i \right)} \right) = \frac{{4\left( {C + D} \right)}}{{3C}}\left( {\frac{5}{2}N + i + \frac{1}{2}} \right)\frac{\Delta }{W}$ | (4) |
其中:4(C+D)/(3C)为总控制时隙和调度控制时隙的比值,Δ为单时隙中的比特数,W为网络总带宽.
令i=N,可得最大调度时延的期望值为
| $E\left( {{T_{\text{D}}}} \right) = \frac{4}{{3\eta }}\left( {\frac{7}{2}N + \frac{1}{2}} \right)\frac{\Delta }{W}$ | (5) |
其中$\eta = \frac{C}{F} = \frac{C}{{C + D}}$为控制时隙所占的比例. 由式(5)可得,调度时延与网络节点个数N、网络总带宽W等网络参数有关,与业务参数无关.
2.2 有效吞吐量模型吞吐量通常定义为节点在不丢包前提下能发送的最大数据速率. 多跳网络中的节点要为邻居节点转发相应业务量,因此笔者将节点不丢包前提下能发送自身业务的最大速率定义为有效吞吐量. 该定义能更准确表征网络的实际数据传输性能.
假设在N个节点组成的集中式多跳网络中存在B条业务流,分别标号为j(j=1,2,…,B),业务流j的跳数设为H(j). 若在时间t内业务流j包含的有效业务量为Ae(j),则整个网络传输的有效数据量为${A_{{\text{e}},{\text{all}}}} = \sum\limits_{j - 1}^B {{A_{\text{e}}}\left( j \right)} $. 考虑转发特性,整个网络中传输的总数据量为${A_{{\text{t}},{\text{all}}}} = \sum\limits_{j - 1}^B {H\left( j \right)A _{\text{e}}\left( j \right)} $.
为保证各业务公平,根据定义可知,有效吞吐量为各节点平均单位时间内传输的有效数据量,即
| $R = E\left( {{A_{\text{e}}}\left( j \right)} \right)/t = {A_{\text{e}}}\left( j \right)/t = {A_{\text{e}}}/t$ | (6) |
1) 数据时隙未占满的情况
假设在调度周期中每个业务源节点请求的数据时隙个数不超过ξ,在数据时隙未占满的情况下有
| ${A_{{\text{e}},{\text{all}}}} = \sum\limits_{j = 1}^B {{A_{\text{e}}}\left( j \right) = B{A_{\text{e}}} = \frac{{tB\xi W\eta }}{{{T_{{\text{acc}}}}}}} $ | (7) |
其中Tacc=4N为控制时隙总个数. 因此有
| $R = \frac{{\xi W\eta }}{{4N}},\eta \leqslant \bar \eta $ | (8) |
2) 数据时隙占满的情况
当没有空闲数据时隙时,网络中传输的总数据量等于所有数据时隙包含的数据量,即
| ${A_{{\text{t}},{\text{all}}}} = \sum\limits_{j = 1}^B {H\left( j \right){A_{\text{e}}}\left( j \right)} = tW\left( {1 - \eta } \right)$ | (9) |
此时,有效吞吐量为
| $R = \frac{{W\left( {1 - \eta } \right)}}{{\sum\limits_{j = 1}^B {H\left( j \right)} }},\eta > \bar \eta $ | (10) |
上述2种情况的临界情况是数据时隙恰好被占满的情况,此时可得使R最大的最优$\bar \eta $为
| $\bar \eta = \frac{{4N}}{{4N + \xi \sum\limits_{j = 1}^B {H\left( j \right)} }}$ | (11) |
由此可以看出,有效吞吐量与网络节点个数N、业务流数目B、各业务流跳数H(j)、控制时隙比例η、最大可预约时隙个数ξ等有关.
3 分析与设计 3.1 时延分析1) 时延与协议参数的关系
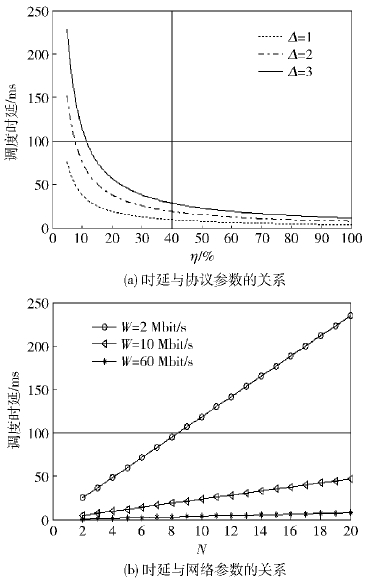
设置N为8,W为10 Mbit/s,时延与η和Δ的关系如图 3(a)所示. 当Δ固定时,时延随着η的增大而减小,因为控制时隙比例越高,完成调度的调度周期个数越少. 当η固定时,时延随着Δ的增大而增大.
在实际场景中时延有具体指标要求,如话音业务时延不超过100 ms. η同时表征信令开销,通常设置为不超过40%. 因此以图 3(a)为例,在Δ=2 kbit时,合适的η取值应在8%~40%之间.
2) 时延与网络参数的关系
图 3(b)给出了当η取40%且Δ取2 kbit时,调度时延与N和W的关系. 同样考虑时延的100 ms限制,可以看出,随着W的增大,网络可支持的最大节点个数也逐渐增多. 如当W取2 Mbit/s时,该网络可支持的最大节点个数为8. 该结论可为不同场景下的节点部署提供指导.
3.2 有效吞吐量分析1) 有效吞吐量与协议参数的关系
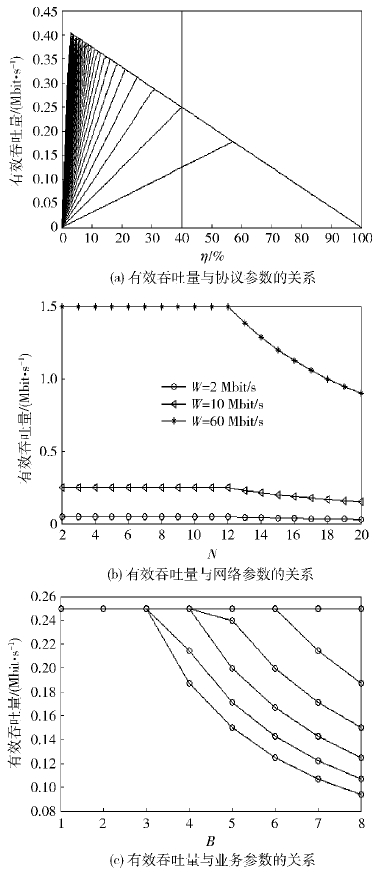
图 4(a)给出了当N为8,W为2 Mbit/s,B为8,业务流平均跳数为$\bar H = \frac{1}{B}\sum\limits_{j = 1}^B {H\left( j \right) = 3} $时,有效吞吐量与η和ξ之间的关系. 若ξ为定值,当η<$\bar \eta $时,数据时隙未占满,有效吞吐量随着η的增大逐渐增大;当η>$\bar \eta $时,数据时隙被占满,有效吞吐量随着η的增大逐渐减小;使有效吞吐量最大的η即为最优的η. 若ξ改变,则最优的η随之改变. 结合时延要求对η的限制,η和ξ取值范围可进一步缩小.
2) 有效吞吐量与网络参数的关系
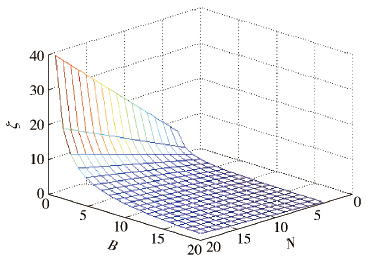
设置η为40%,ξ为2,B为8,$\bar H = 3$,有效吞吐量与N和W之间的关系如图 4(b)所示. 若W固定,N小于一定阈值时,有效吞吐量保持在较高水平;若N进一步增多,有效吞吐量会快速恶化;当N确定时,增大W可使有效吞吐量成倍增长.
3) 有效吞吐量与业务参数的关系
设置η为40%,ξ为2,N为8,W为10 Mbit/s,有效吞吐量与B和$\bar H$的关系如图 4(c)所示. 当$\bar H$固定,B限制在一定范围内时,有效吞吐量保持在较高水平;若B进一步增大,有效吞吐量快速下降;当B固定,$\bar H$限制在一定范围内时,有效吞吐量保持在较高水平;$\bar H$进一步增大,导致有效吞吐量快速下降. 这是由于超过一定阈值后,节点转发业务量急剧增大,从而降低了节点的有效吞吐量.
3.3 协议参数设计基于图 3(a)的结论,信令开销40%的限制决定了η的最大取值,此时调度时延也为最优. 在此前提下,图 5给出了不同网络场景和业务需求条件下ξ的最优取值. N越多,B越小,最优的ξ取值越高. 按照该策略设计的协议参数可保证调度时延和有效吞吐量同时达到优化.
4 结束语在基于预约方式的集中式调度协议框架基础上,充分考虑网络参数、业务参数和协议参数的影响,建立了集中式多跳网络调度时延模型和有效吞吐量模型. 数值仿真结果表明,网络节点个数、网络总带宽、业务流数目、平均跳数、控制时隙比例、最大可预约时隙个数等参数与系统性能之间存在定量关系. 最后给出了特定网络场景和业务需求条件下的协议参数设计策略. 该结论将为工程应用中的协议参数设计和优化提供重要参考.
| [1] | Wang Poyuan, Liang Shihtsung. Performance comparisons of the routing tree construction algorithms for IEEE 802. 16 centralized scheduling mesh networks[C]//2014 Sixth International Conf on Ubiquitous and Future Networks (ICUFN). Shanghai:IEEE, 2014:40-45.[引用本文:1] |
| [2] | Hillebrand F. The creation of standards for global mobile communication:GSM and UMTS standardization from 1982 to 2000[J]. IEEE Wireless Communications, 2013, 20(5):24-33.[引用本文:1] |
| [3] | Ahmed B T. WCDMA downlink capacity of cigar-shaped microcells for long tunnels[J]. Telecommunication Systems, 2014, 57(57):229-237.[引用本文:1] |
| [4] | Davydov A, Morozov G, Bolotin I, et al. Evaluation of joint transmission CoMP in C-RAN based LTE-A HetNets with large coordination areas[C]//IEEE GLOBECOM Workshops. Atlanta, GA:IEEE, 2013:801-806.[引用本文:1] |
| [5] | Liu Tingting, Yang Chenyang, Yang Lieliang. A unified analysis of spectral efficiency for two-hop relay systems with different resource configurations[J]. IEEE Transactions on Vehicular Technology, 2013, 62(62):3137-3148.[引用本文:1] |
| [6] | IEEE. IEEE std 802. 16-2004(revision of IEEE std 802. 16-2001)-2004, IEEE standard for local and metropolitan area networks part 16:air interface for fixed broadband wireless access systems[S]. USA:IEEE, 2004:1-857.[引用本文:1] |
| [7] | Tang Yuliang, Liu Zhixiong, Huang Lianfen, et al. Dynamic frame partitioning scheme for IEEE 802. 16 mesh networks[J]. Wireless Communications and Mobile Computing, 2014, 14(11):1045-1054.[引用本文:1] |